Exceptional Points through Variation of Distances between Four Coaxial Dielectric Disks
Abstract
:1. Introduction
2. Exceptional Points in Single Disk
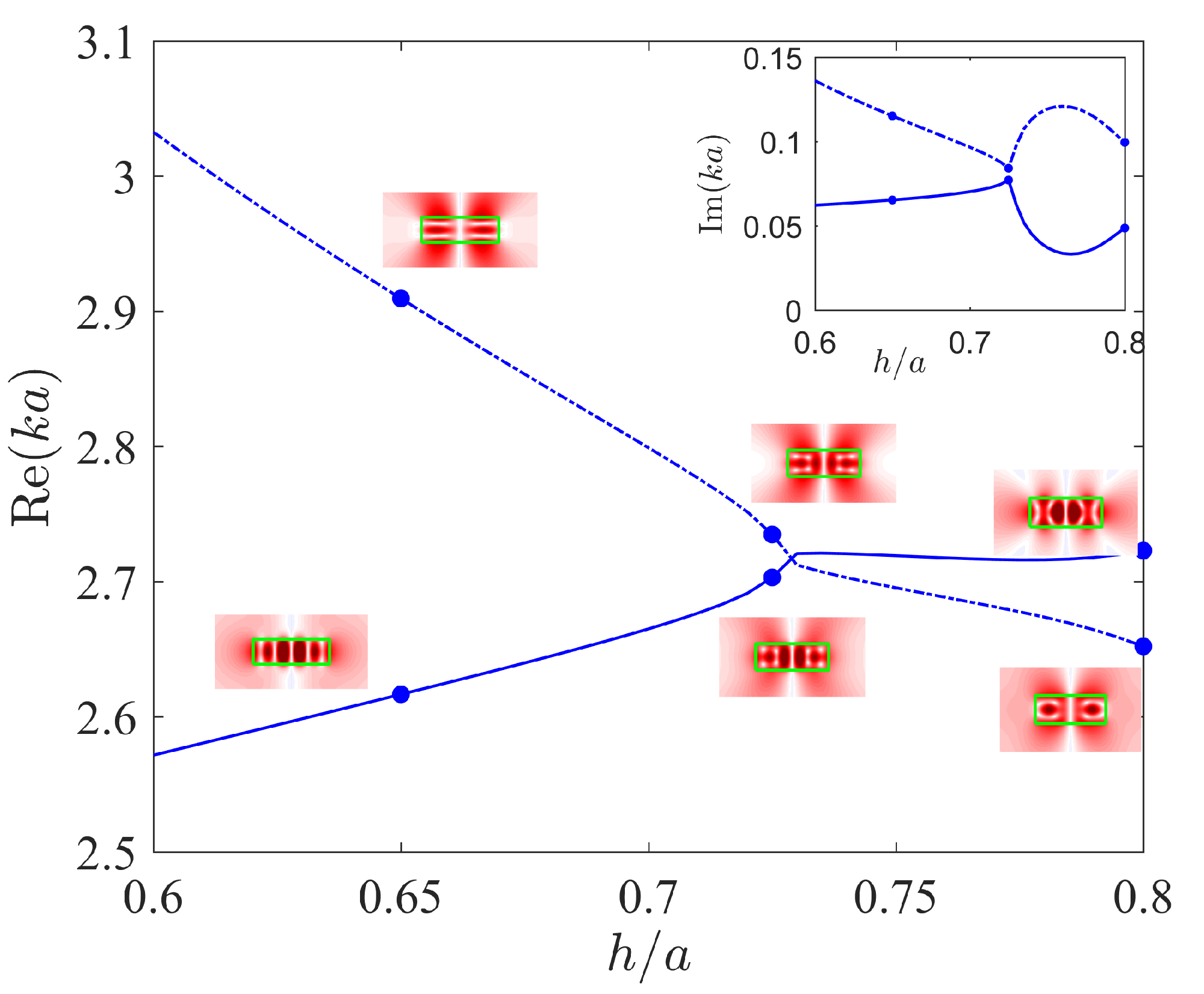
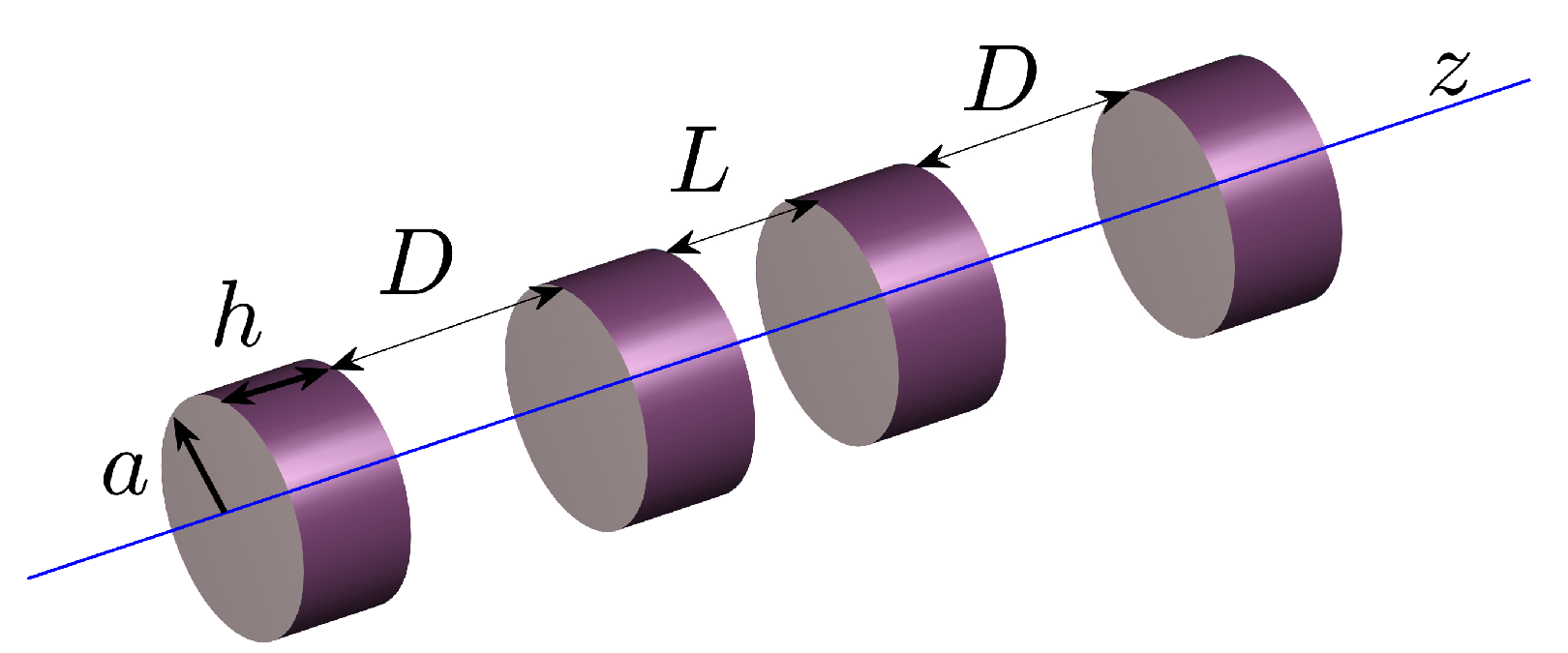
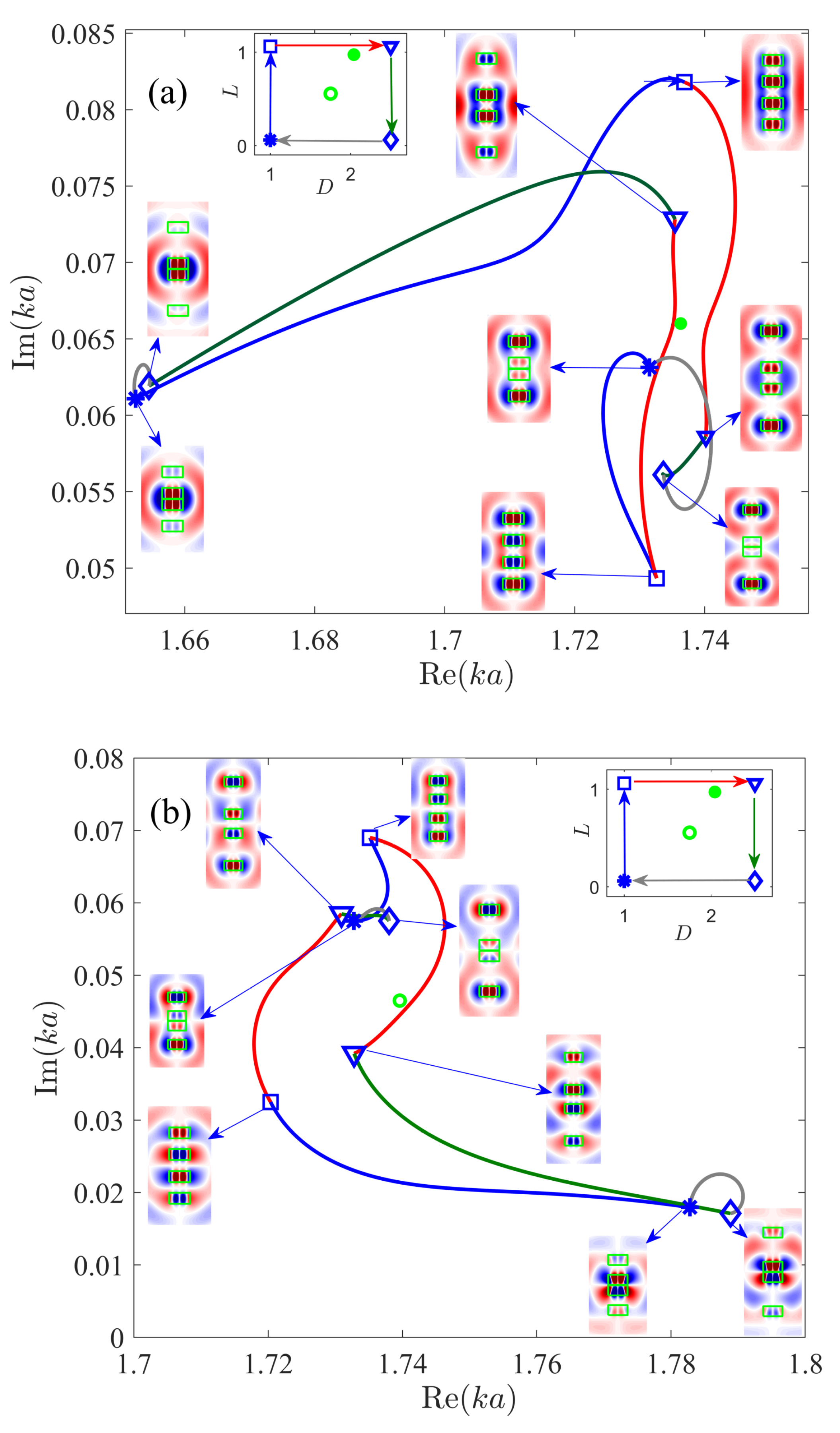
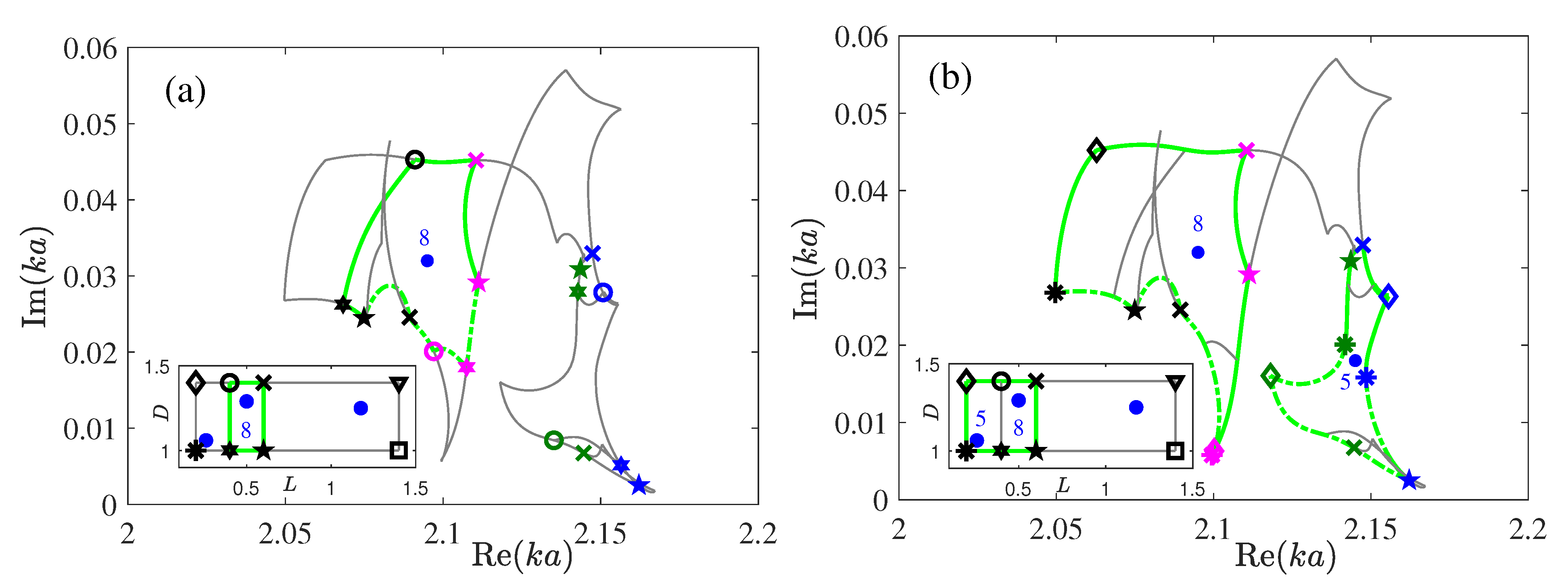
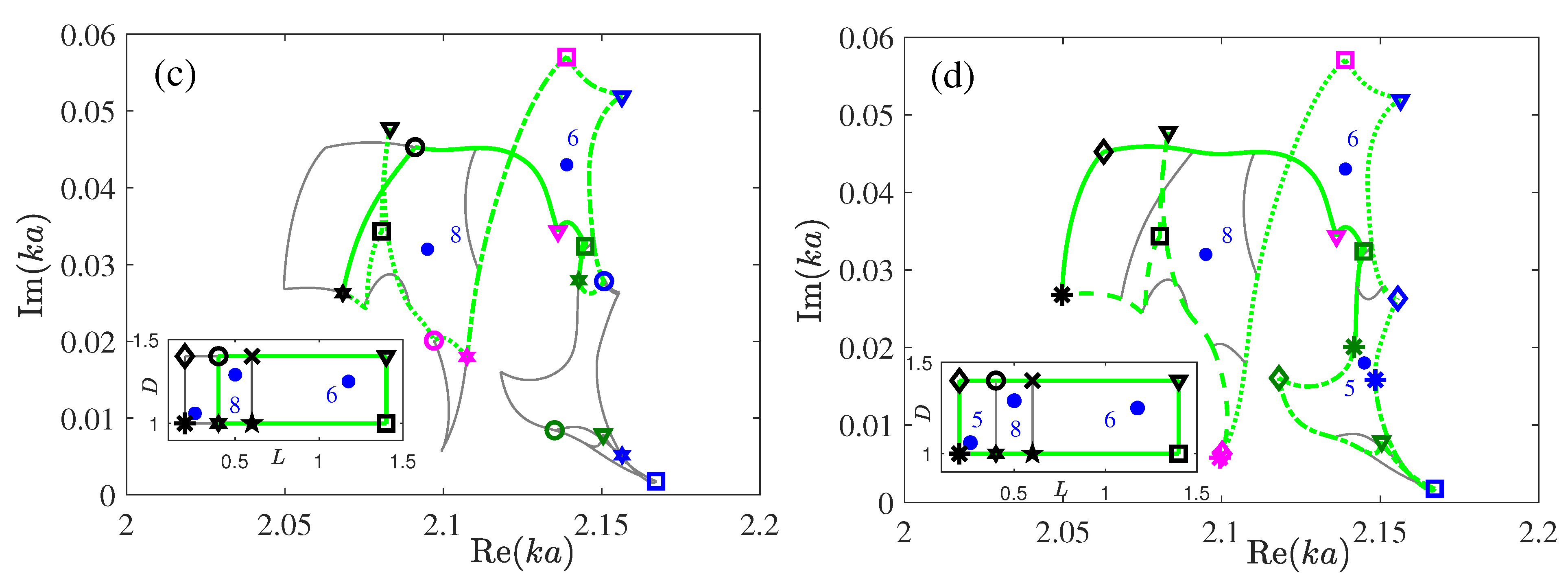
3. Two-Scale Variation of Distances in the System of Four Coaxial Disks
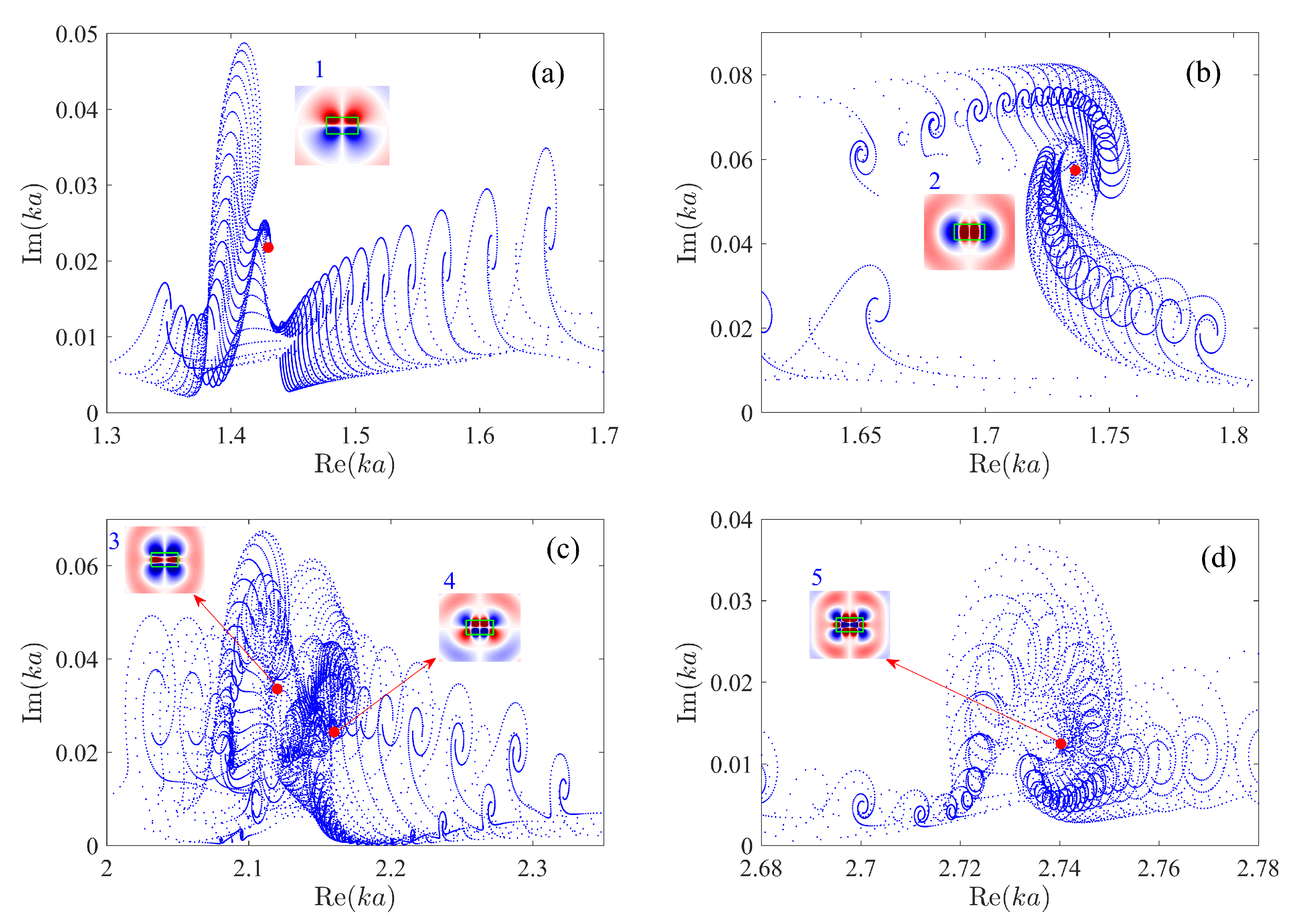
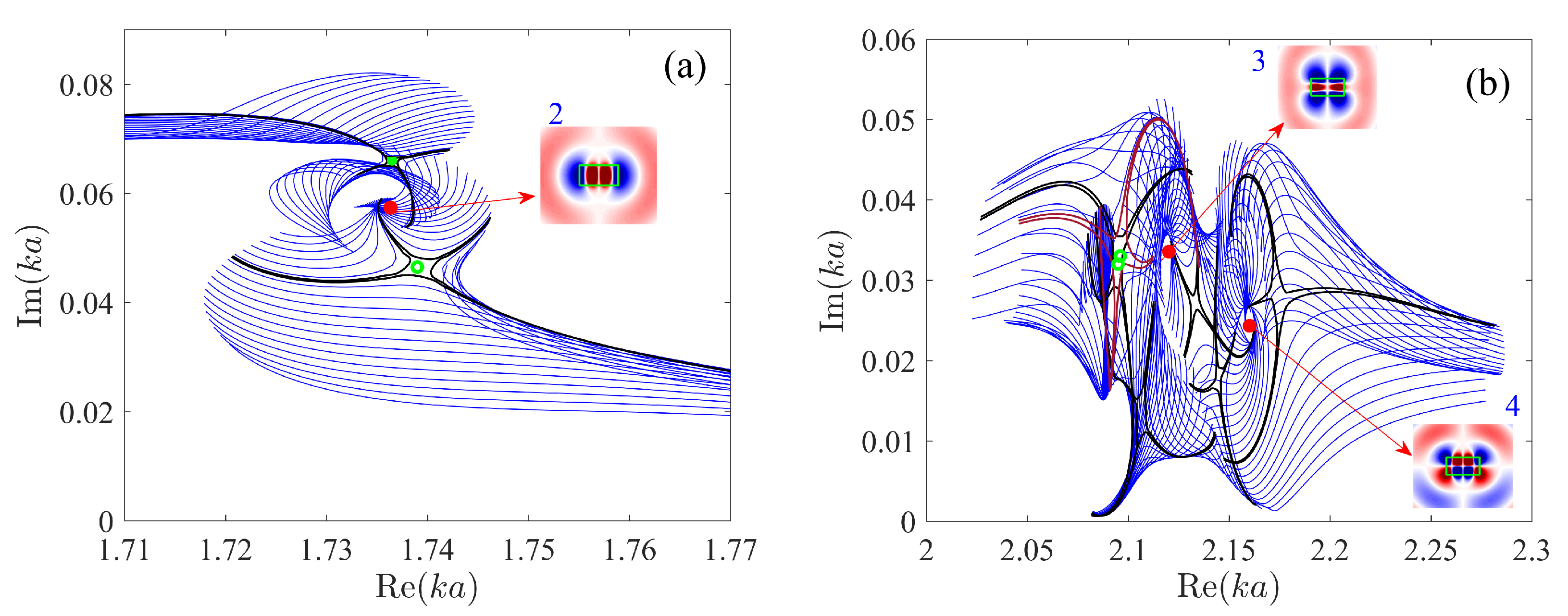
4. Exceptional Points in System of Four Disks
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Heiss, W.D.; Sannino, A.L. Avoided level crossing and exceptional points. J. Phys. A Math. Gen. 1990, 23, 1167–1178. [Google Scholar] [CrossRef] [Green Version]
- Heiss, W. Phases of wave functions and level repulsion. Eur. Phys. J. D Atom. Mol. Opt. Phys. 1999, 7, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Zhu, X.; Yang, S.; Zhu, H.; Zhang, P.; Yin, X.; Wang, Y.; Zhang, X. Demonstration of a large-scale optical exceptional point structure. Opt. Express 2013, 22, 1760–1767. [Google Scholar] [CrossRef]
- Brandstetter, M.; Liertzer, M.; Deutsch, C.; Klang, P.; Schöberl, J.; Türeci, H.E.; Strasser, G.; Unterrainer, K.; Rotter, S. Reversing the pump dependence of a laser at an exceptional point. Nat. Commun. 2014, 5, 4034. [Google Scholar] [CrossRef] [Green Version]
- Longhi, S. Parity-time symmetry meets photonics: A new twist in non-Hermitian optics. EPL (Europhys. Lett.) 2017, 120, 64001. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; El-Ganainy, R.; Ge, L. Non-Hermitian photonics based on parity–time symmetry. Nat. Photonics 2017, 11, 752–762. [Google Scholar] [CrossRef]
- Oezdemir, Ş.K.; Rotter, S.; Nori, F.; Yang, L. Parity–time symmetry and exceptional points in photonics. Nat. Mater. 2019, 18, 783–798. [Google Scholar] [CrossRef]
- Miri, M.A.; Alù, A. Exceptional points in optics and photonics. Science 2019, 363, 7709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, L.; Wong, Z.J.; Ma, R.M.; Wang, Y.; Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 2014, 346, 972–975. [Google Scholar] [CrossRef]
- Ghosh, S.N.; Chong, Y.D. Exceptional points and asymmetric mode conversion in quasi-guided dual-mode optical waveguides. Sci. Rep. 2016, 6, 19837. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Ayache, M.; Huang, J.; Xu, Y.L.; Lu, M.H.; Chen, Y.F.; Fainman, Y.; Scherer, A. Nonreciprocal Light Propagation in a Silicon Photonic Circuit. Science 2011, 333, 729–733. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laha, A.; Dey, S.; Gandhi, H.K.; Biswas, A.; Ghosh, S. Exceptional Point and toward Mode-Selective Optical Isolation. ACS Photonics 2020, 7, 967–974. [Google Scholar] [CrossRef]
- Chen, W.; Özdemir, Ş.K.; Zhao, G.; Wiersig, J.; Yang, L. Exceptional points enhance sensing in an optical microcavity. Nature 2017, 548, 192–196. [Google Scholar] [CrossRef]
- Zhen, B.; Hsu, C.W.; Igarashi, Y.; Lu, L.; Kaminer, I.; Pick, A.; Chua, S.L.; Joannopoulos, J.; Soljačić, M. Spawning rings of exceptional points out of Dirac cones. Nature 2015, 525, 354–358. [Google Scholar] [CrossRef]
- Kamiński, P.M.; Taghizadeh, A.; Breinbjerg, O.; Mørk, J.; Arslanagić, S. Control of exceptional points in photonic crystal slabs. Opt. Lett. 2017, 42, 2866. [Google Scholar] [CrossRef]
- Abdrabou, A.; Lu, Y.Y. Exceptional points of resonant states on a periodic slab. Phys. Rev. A 2018, 97, 063822. [Google Scholar] [CrossRef] [Green Version]
- Abdrabou, A.; Lu, Y.Y. Exceptional points of Bloch eigenmodes on a dielectric slab with a periodic array of cylinders. Phys. Scr. 2020, 95, 095507. [Google Scholar] [CrossRef]
- Min, S.Y.; Kim, J.Y.; Yu, S.; Menabde, S.G.; Jang, M.S. Exceptional Points in Plasmonic Waveguides Do Not Require Gain or Loss. Phys. Rev. Appl. 2020, 14, 054041. [Google Scholar] [CrossRef]
- Popov, V.; Tretyakov, S.; Novitsky, A. Brewster effect when approaching exceptional points of degeneracy: Epsilon-near-zero behavior. Phys. Rev. B 2019, 99, 045146. [Google Scholar] [CrossRef] [Green Version]
- Ryu, J.W.; Lee, S.Y.; Kim, S.W. Analysis of multiple exceptional points related to three interacting eigenmodes in a non-Hermitian Hamiltonian. Phys. Rev. A 2012, 85, 042101. [Google Scholar] [CrossRef] [Green Version]
- Kullig, J.; Yi, C.H.; Hentschel, M.; Wiersig, J. Exceptional points of third-order in a layered optical microdisk cavity. New J. Phys. 2018, 20, 083016. [Google Scholar] [CrossRef]
- Yi, C.H.; Kullig, J.; Hentschel, M.; Wiersig, J. Non-Hermitian degeneracies of internal–external mode pairs in dielectric microdisks. Photonics Res. 2019, 7, 464. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, Y.; Veronis, G. Non-PT-symmetric two-layer cylindrical waveguide for exceptional-point-enhanced optical devices. Opt. Express 2019, 27, 37494. [Google Scholar] [CrossRef]
- Abdrabou, A.; Lu, Y.Y. Exceptional points for resonant states on parallel circular dielectric cylinders. J. Opt. Soc. Am. B 2019, 36, 1659. [Google Scholar] [CrossRef]
- Unterhinninghofen, J.; Wiersig, J.; Hentschel, M. Goos-Hänchen shift and localization of optical modes in deformed microcavities. Phys. Rev. E 2008, 78, 016201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kullig, J.; Wiersig, J. Perturbation theory for asymmetric deformed microdisk cavities. Phys. Rev. A 2016, 94, 043850. [Google Scholar] [CrossRef]
- Kullig, J.; Yi, C.H.; Wiersig, J. Exceptional points by coupling of modes with different angular momenta in deformed microdisks: A perturbative analysis. Phys. Rev. A 2018, 98, 023851. [Google Scholar] [CrossRef]
- Jiang, T.; Xiang, Y. Perturbation model for optical modes in deformed disks. Phys. Rev. A 2019, 99, 023847. [Google Scholar] [CrossRef]
- Lee, S.B.; Yang, J.; Moon, S.; Lee, S.Y.; Shim, J.B.; Kim, S.W.; Lee, J.H.; An, K. Observation of an Exceptional Point in a Chaotic Optical Microcavity. Phys. Rev. Lett. 2009, 103, 134101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, T.; Xiang, Y. Perfectly-matched-layer method for optical modes in dielectric cavities. Phys. Rev. A 2020, 102, 053704. [Google Scholar] [CrossRef]
- Bulgakov, E.; Pichugin, K.; Sadreev, A. Exceptional points in dielectric spheroid. arXiv 2021, arXiv:2107.13719. [Google Scholar]
- Kodigala, A.; Lepetit, T.; Kanté, B. Exceptional points in three-dimensional plasmonic nanostructures. Phys. Rev. B 2016, 94, 201103. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.Y.; Ryu, J.W.; Kim, S.W.; Chung, Y. Geometric phase around multiple exceptional points. Phys. Rev. A 2012, 85, 064103. [Google Scholar] [CrossRef]
- Ding, K.; Ma, G.; Xiao, M.; Zhang, Z.; Chan, C. Emergence, Coalescence, and Topological Properties of Multiple Exceptional Points and Their Experimental Realization. Phys. Rev. X 2016, 6, 021007. [Google Scholar] [CrossRef]
- Pick, A.; Zhen, B.; Miller, O.; Hsu, C.W.; Hernandez, F.; Rodriguez, A.; Soljačić, M.; Johnson, S. General theory of spontaneous emission near exceptional points. Opt. Express 2017, 25, 12325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rybin, M.V.; Koshelev, K.L.; Sadrieva, Z.F.; Samusev, K.B.; Bogdanov, A.A.; Limonov, M.F.; Kivshar, Y.S. High-Q Supercavity Modes in Subwavelength Dielectric Resonators. Phys. Rev. Lett. 2017, 119, 243901. [Google Scholar] [CrossRef] [Green Version]
- Pichugin, K.N.; Sadreev, A.F. Interaction between coaxial dielectric disks enhances the Q factor. J. Appl. Phys. 2019, 126, 093105. [Google Scholar] [CrossRef] [Green Version]
- Bogdanov, A.A.; Koshelev, K.L.; Kapitanova, P.V.; Rybin, M.V.; Gladyshev, S.A.; Sadrieva, Z.F.; Samusev, K.B.; Kivshar, Y.S.; Limonov, M.F. Bound states in the continuum and Fano resonances in the strong mode coupling regime. Adv. Photonics 2019, 1, 1. [Google Scholar] [CrossRef]
- Odit, M.; Koshelev, K.; Gladyshev, S.; Ladutenko, K.; Kivshar, Y.; Bogdanov, A. Observation of Supercavity Modes in Subwavelength Dielectric Resonators. Adv. Mater. 2020, 33, 2003804. [Google Scholar] [CrossRef]
- Awai, I.; Zhang, Y. Coupling coefficient of resonators—An intuitive way of its understanding. Electron. Commun. Jpn. (Part II Electron.) 2007, 90, 11–18. [Google Scholar] [CrossRef]
- Elnaggar, S.Y.; Tervo, R.J.; Mattar, S.M. General expressions and physical origin of the coupling coefficient of arbitrary tuned coupled electromagnetic resonators. J. Appl. Phys. 2015, 118, 194901. [Google Scholar] [CrossRef]
- Dembowski, C.; Graf, H.D.; Harney, H.L.; Heine, A.; Heiss, W.D.; Rehfeld, H.; Richter, A. Experimental Observation of the Topological Structure of Exceptional Points. Phys. Rev. Lett. 2001, 86, 787–790. [Google Scholar] [CrossRef] [PubMed]
- Stehmann, T.; Heiss, W.D.; Scholtz, F.G. Observation of exceptional points in electronic circuits. J. Phys. A Math. Gen. 2004, 37, 7813–7819. [Google Scholar] [CrossRef]
- Bulgakov, E.; Pichugin, K.; Sadreev, A. Mie Resonance Engineering in Two Disks. Photonics 2021, 8, 49. [Google Scholar] [CrossRef]
- Demange, G.; Graefe, E.M. Signatures of three coalescing eigenfunctions. J. Phys. A Math. Theor. 2011, 45, 025303. [Google Scholar] [CrossRef]
- Zhang, X.L.; Wang, S.; Hou, B.; Chan, C. Dynamically Encircling Exceptional Points: In situ Control of Encircling Loops and the Role of the Starting Point. Phys. Rev. X 2018, 8, 021066. [Google Scholar] [CrossRef] [Green Version]
- Jaiswal, R.; Banerjee, A.; Narayan, A. Characterizing and Tuning Exceptional Points Using Newton Polygons. arXiv 2021, arXiv:2107.11649. [Google Scholar]
- Zhong, Q.; Khajavikhan, M.; Christodoulides, D.N.; El-Ganainy, R. Winding around non-Hermitian singularities. Nat. Commun. 2018, 9, 4808. [Google Scholar] [CrossRef]
- Uzdin, R.; Mailybaev, A.; Moiseyev, N. On the observability and asymmetry of adiabatic state flips generated by exceptional points. J. Phys. A Math. Theor. 2011, 44, 435302. [Google Scholar] [CrossRef] [Green Version]
| Symmetric | Anti-Symmetric | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1.736 + 0.066i | 2.04 | 0.97 | 1 | 1.739 + 0.046i | 1.75 | 0.56 |
| 2 | 2.030 + 0.006i | 0.14 | 0.07 | 2 | 1.734 + 0.060i | 3.20 | 2.35 |
| 3 | 2.050 + 0.006i | 0.22 | 0.12 | 3 | 2.110 + 0.013i | 0.23 | 0.65 |
| 4 | 2.152 + 0.044i | 0.55 | 1.67 | 4 | 2.145 + 0.020i | 0.46 | 0.07 |
| 5 | 2.145 + 0.018i | 1.06 | 0.26 | 5 | 2.152 + 0.036i | 0.67 | 3.38 |
| 6 | 2.139 + 0.043i | 1.25 | 1.18 | 6 | 2.147 + 0.019i | 0.72 | 1.63 |
| 7 | 2.150 + 0.026i | 1.26 | 2.79 | 7 | 2.141 + 0.035i | 1.00 | 2.65 |
| 8 | 2.095 + 0.032i | 1.29 | 0.50 | 8 | 2.175 + 0.028i | 1.53 | 0.35 |
| 9 | 2.106 + 0.013i | 1.56 | 0.23 | 9 | 2.133 + 0.028i | 2.20 | 0.90 |
| 10 | 2.139 + 0.023i | 1.69 | 1.43 | 10 | 2.133 + 0.025i | 2.32 | 1.96 |
| 11 | 2.096 + 0.034i | 1.73 | 0.21 | 11 | 2.120 + 0.024i | 2.46 | 2.03 |
| 12 | 2.110 + 0.042i | 2.68 | 1.42 | 12 | 2.158 + 0.013i | 2.76 | 1.44 |
| 13 | 2.166 + 0.024i | 2.92 | 2.22 | 13 | 2.145 + 0.023i | 2.88 | 1.52 |
| 14 | 2.116 + 0.024i | 3.08 | 0.32 | 14 | 2.169 + 0.027i | 3.20 | 0.48 |
| 15 | 2.148 + 0.025i | 3.15 | 0.63 | 15 | 2.152 + 0.026i | 3.25 | 1.03 |
| 16 | 2.165 + 0.022i | 3.22 | 2.40 | 16 | 2.116 + 0.031i | 3.84 | 2.66 |
| 17 | 2.127 + 0.030i | 3.68 | 0.60 | 17 | 2.1769 + 0.001i | 0.901 | 0.866 |
| 18 | 2.162 + 0.031i | 3.80 | 1.67 | 18 | 2.1757 + 0.001i | 0.929 | 0.872 |
| D | L | |||||
|---|---|---|---|---|---|---|
 | 1 | 0.2 |  |  |  |  |
 | 1 | 0.4 |  |  |  |  |
 | 1 | 0.6 |  |  |  |  |
 | 1 | 1.4 |  |  |  |  |
 | 1.4 | 0.2 |  | 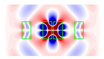 |  | 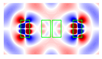 |
 | 1.4 | 0.4 |  | 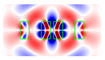 | 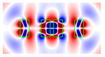 | 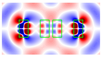 |
 | 1.4 | 0.6 |  |  | 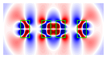 | 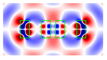 |
 | 1.4 | 1.4 | 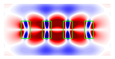 |  | 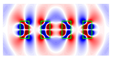 | 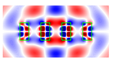 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pichugin, K.; Sadreev, A.; Bulgakov, E. Exceptional Points through Variation of Distances between Four Coaxial Dielectric Disks. Photonics 2021, 8, 460. https://doi.org/10.3390/photonics8110460
Pichugin K, Sadreev A, Bulgakov E. Exceptional Points through Variation of Distances between Four Coaxial Dielectric Disks. Photonics. 2021; 8(11):460. https://doi.org/10.3390/photonics8110460
Chicago/Turabian StylePichugin, Konstantin, Almas Sadreev, and Evgeny Bulgakov. 2021. "Exceptional Points through Variation of Distances between Four Coaxial Dielectric Disks" Photonics 8, no. 11: 460. https://doi.org/10.3390/photonics8110460





