Optical Wireless Communications Using Signal Space Diversity with Spatial Modulation
Abstract
:1. Introduction
2. Principle and Theoretical BER Expressions of the SSD Scheme Incorporated with SM in a 2 × 1 MISO OWC System
2.1. 2 × 1 MISO OWC System Configuration and Spatial Modulation Implementation
2.2. Principle of the SSD Scheme Incorporated with SM
2.3. Theoretical BER Expressions
3. Results
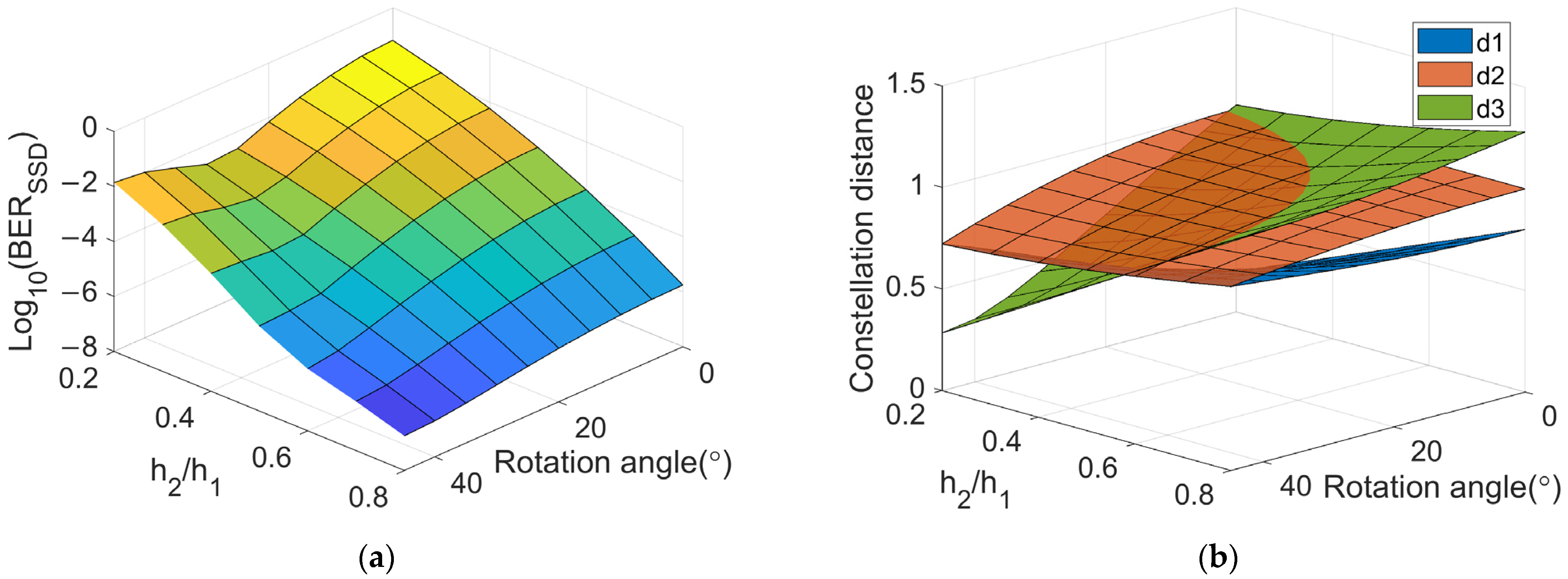
3.1. Analysis of the Theoretical and Numerical BER Results
3.2. Theoretical Investigation of Channel Gain Distributions at Different Signal Constellation Rotation Angles to Improve the BER Performance
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BER | Bit-error-rate |
| CAP | Carrierless Amplitude and Phase Modulation |
| IM/DD | Intensity Modulation/Direct Detection |
| LOS | Line-of-sight |
| MFs | Matched Filters |
| MIMO | Multiple-input-multiple-output |
| MISO | Multiple-input-single-output |
| ML | Maximum Likelihood |
| OWC | Optical Wireless Communication |
| QAM | Quadrature Amplitude Modulation |
| RF | Radio Frequency |
| SM | Spatial Modulation |
| SMux | Spatial Multiplexing |
| SSD | Signal Space Diversity |
References
- Cisco Annual Internet Report (2018–2023) White Paper. Available online: https://www.cisco.com/c/en/us/solutions/collateral/executive-perspectives/annual-internet-report/white-paper-c11-741490.html (accessed on 1 September 2021).
- Koonen, T. Indoor Optical Wireless Systems: Technology, Trends, and Applications. J. Light. Technol. 2017, 36, 1459–1467. [Google Scholar] [CrossRef]
- Fiber to the Premises. Available online: https://www.corning.com/fiber-to-the-premise/worldwide/en/home.html (accessed on 1 September 2021).
- Kahn, J.M.; Barry, J.R. Wireless infrared communications. Proc. IEEE 1997, 85, 265–298. [Google Scholar] [CrossRef] [Green Version]
- Ghassemlooy, Z.; Arnon, S.; Uysal, M.; Xu, Z.; Cheng, J. Emerging Optical Wireless Communications-Advances and Challenges. IEEE J. Sel. Areas Commun. 2015, 33, 1738–1749. [Google Scholar] [CrossRef]
- Berenguer, P.W.; Hellwig, P.; Schulz, D.; Hilt, J.; Kleinpeter, G.; Fischer, J.K.; Jungnickel, V. Real-Time Optical Wireless Mobile Communication With High Physical Layer Reliability. J. Light. Technol. 2019, 37, 1638–1646. [Google Scholar] [CrossRef]
- Song, T.; Nirmalathas, A.; Lim, C.; Wong, E.; Lee, K.-L.; Hong, Y.; Alameh, K.; Wang, K. Performance Analysis of Repetition-Coding and Space-Time-Block-Coding as Transmitter Diversity Schemes for Indoor Optical Wireless Communications. J. Light. Technol. 2019, 37, 5170–5177. [Google Scholar] [CrossRef]
- Fath, T.; Haas, H. Performance Comparison of MIMO Techniques for Optical Wireless Communications in Indoor Environments. IEEE Trans. Commun. 2012, 61, 733–742. [Google Scholar] [CrossRef]
- Chen, T.; Zhens, Z.; Liu, L.; Hu, W. High-diversity space division multiplexing visible light communication utilising a fisheye-lens-based imaging receiver. In Proceedings of the 2015 Optical Fiber Communications Conference and Exhibition (OFC) IEEE, Los Angeles, CA, USA, 22–26 March 2015; pp. 1–3. [Google Scholar]
- Guo, X.; Chi, N. Superposed 32QAM Constellation Design for 2 × 2 Spatial Multiplexing MIMO VLC Systems. J. Light. Technol. 2019, 38, 1702–1711. [Google Scholar] [CrossRef]
- Liu, L.; Deng, R.; Shi, J.; He, J.; Chen, L.-K. Beyond 100-kbit/s Transmission over Rolling Shutter Camera-based VLC Enabled by Color and Spatial Multiplexing. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020. [Google Scholar] [CrossRef]
- Jaiswal, A.; Abaza, M.; Bhatnagar, M.R.; Jain, V.K. An Investigation of Performance and Diversity Property of Optical Space Shift Keying-Based FSO-MIMO System. IEEE Trans. Commun. 2018, 66, 4028–4042. [Google Scholar] [CrossRef]
- Cogalan, T.; Haas, H.; Panayirci, E. Optical spatial modulation design. Philos. Trans. R. Soc. A 2020, 378, 2169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abou-Rjeily, C.; Kaddoum, G. Optical Spatial Modulation for FSO IM/DD Communications with Photon-Counting Receivers: Performance Analysis, Transmit Diversity Order and Aperture Selection. IEEE J. Sel. Areas Commun. 2019, 37, 2053–2068. [Google Scholar] [CrossRef]
- Renzo, M.D.; Haas, H. On transmit diversity for spatial modulation MIMO: Impact of spatial constellation diagram and shaping filters at the transmitter. IEEE Trans. Veh. Technol. 2013, 62, 2507–2531. [Google Scholar] [CrossRef] [Green Version]
- Althunibat, S.; Mesleh, R. Enhancing Spatial Modulation System Performance Through Signal Space Diversity. IEEE Commun. Lett. 2018, 22, 1136–1139. [Google Scholar] [CrossRef]
- Boutros, J.; Viterbo, E. Signal space diversity: A power- and bandwidth-efficient diversity technique for the Rayleigh fading channel. IEEE Trans. Inf. Theory 1998, 44, 1453–1467. [Google Scholar] [CrossRef] [Green Version]
- Kiyani, N.F.; Weber, J.H.; Zajic, A.G.; Stuber, G.L. Performance Analysis of a System using Coordinate Interleaving and Constellation Rotation in Rayleigh Fading Channels. In Proceedings of the 2008 IEEE 68th Vehicular Technology Conference, Calgary, AB, Canada, 21–24 September 2008. [Google Scholar] [CrossRef]
- Yusuf, M.; Arslan, H. On signal space diversity: An adaptive interleaver for enhancing physical layer security in frequency selective fading channels. Phys. Commun. 2017, 24, 154–160. [Google Scholar] [CrossRef]
- Song, T.; Wang, K.; Nirmalathas, A.; Lim, C.; Wong, E.; Alameh, K. Demonstration of Optical Wireless Communications using Spatial Modulation with Signal Space Diversity. In Proceedings of the 2019 IEEE Photonics Conference (IPC), San Antonio, TX, USA, 29 September–3 October 2019. [Google Scholar] [CrossRef]
- Proakis, J.G.; Salehi, M. Digital Communications, 5th ed.; McGraw-Hill Higher Education: New York, NY, USA, 2008; pp. 160–242. [Google Scholar]
- Cho, K.; Yoon, D. On the general BER expression of one- and two-dimensional amplitude modulations. IEEE Trans. Commun. 2002, 50, 1074–1080. [Google Scholar] [CrossRef] [Green Version]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with Matlab®, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2019; pp. 397–456. [Google Scholar]


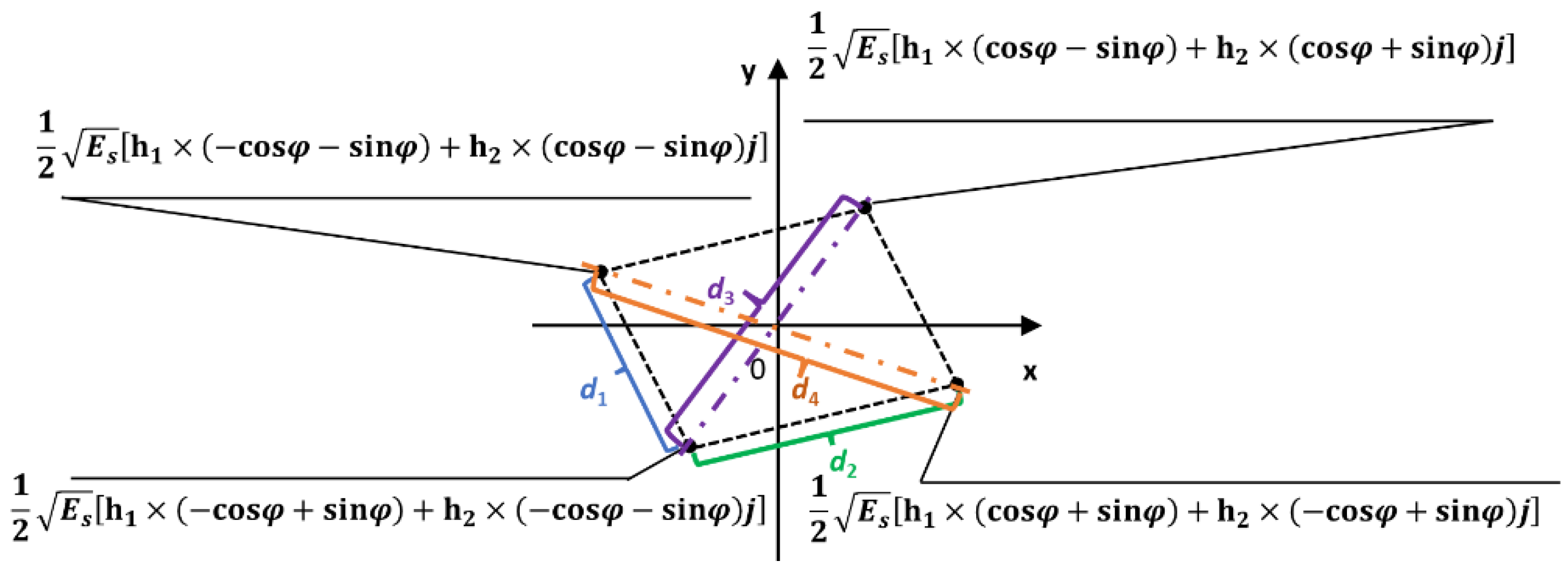


| Items | ||||
|---|---|---|---|---|
| 1, 0.63, 20° (Figure 4a, red) | 0.684 | 0.964 | 1.005 | Yes (Equation (15)) |
| 1, 0.63, 45° (Figure 4a, blue) | 0.836 | 0.836 | 0.89 | Yes (Equation (15)) |
| 1, 0.3, 20° (Figure 4b, black) | 0.443 | 0.945 | 0.711 | Yes (Equation (15)) |
| 1, 0.3, 30° (Figure 4b, red) | 0.563 | 0.879 | 0.549 | No (Equation (16)) |
| 1, 0.5, 30° (Figure 4b, blue) | 0.661 | 0.901 | 0.775 | Yes (Equation (15)) |
| 1, 0.5, 45° (Figure 4b,c, purple) | 0.791 | 0.791 | 0.707 | No (Equation (16)) |
| 1, 0.3, 45° (Figure 4c, yellow) | 0.738 | 0.738 | 0.424 | No (Equation (16)) |
| 1, 0.4, 45° (Figure 4c, grey) | 0.762 | 0.762 | 0.566 | No (Equation (16)) |
| 1, 0.6, 45° (Figure 4c, green) | 0.825 | 0.825 | 0.849 | Yes (Equation (15)) |
| 1, 0.3, 29.5° (Figure 4d, black) | 0.557 | 0.883 | 0.557 | No (Equation (16)) |
| 1, 0.4, 32.4° (Figure 4d, red) | 0.633 | 0.871 | 0.632 | No (Equation (16)) |
| 1, 0.5, 37.4° (Figure 4d, blue) | 0.726 | 0.851 | 0.725 | No (Equation (16)) |
| 1, 0.57, 44° (Figure 4d, orange) | 0.807 | 0.821 | 0.806 | No (Equation (16)) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, T.; Lim, C.; Nirmalathas, A.; Wang, K. Optical Wireless Communications Using Signal Space Diversity with Spatial Modulation. Photonics 2021, 8, 468. https://doi.org/10.3390/photonics8110468
Song T, Lim C, Nirmalathas A, Wang K. Optical Wireless Communications Using Signal Space Diversity with Spatial Modulation. Photonics. 2021; 8(11):468. https://doi.org/10.3390/photonics8110468
Chicago/Turabian StyleSong, Tingting, Christina Lim, Ampalavanapillai Nirmalathas, and Ke Wang. 2021. "Optical Wireless Communications Using Signal Space Diversity with Spatial Modulation" Photonics 8, no. 11: 468. https://doi.org/10.3390/photonics8110468
APA StyleSong, T., Lim, C., Nirmalathas, A., & Wang, K. (2021). Optical Wireless Communications Using Signal Space Diversity with Spatial Modulation. Photonics, 8(11), 468. https://doi.org/10.3390/photonics8110468





