Theoretical Demonstration of Security Improvement of Optical Phased Array Based on Optically Injection-Locked Lasers
Abstract
:1. Introduction
2. Security Model of OPA-Based OWC System
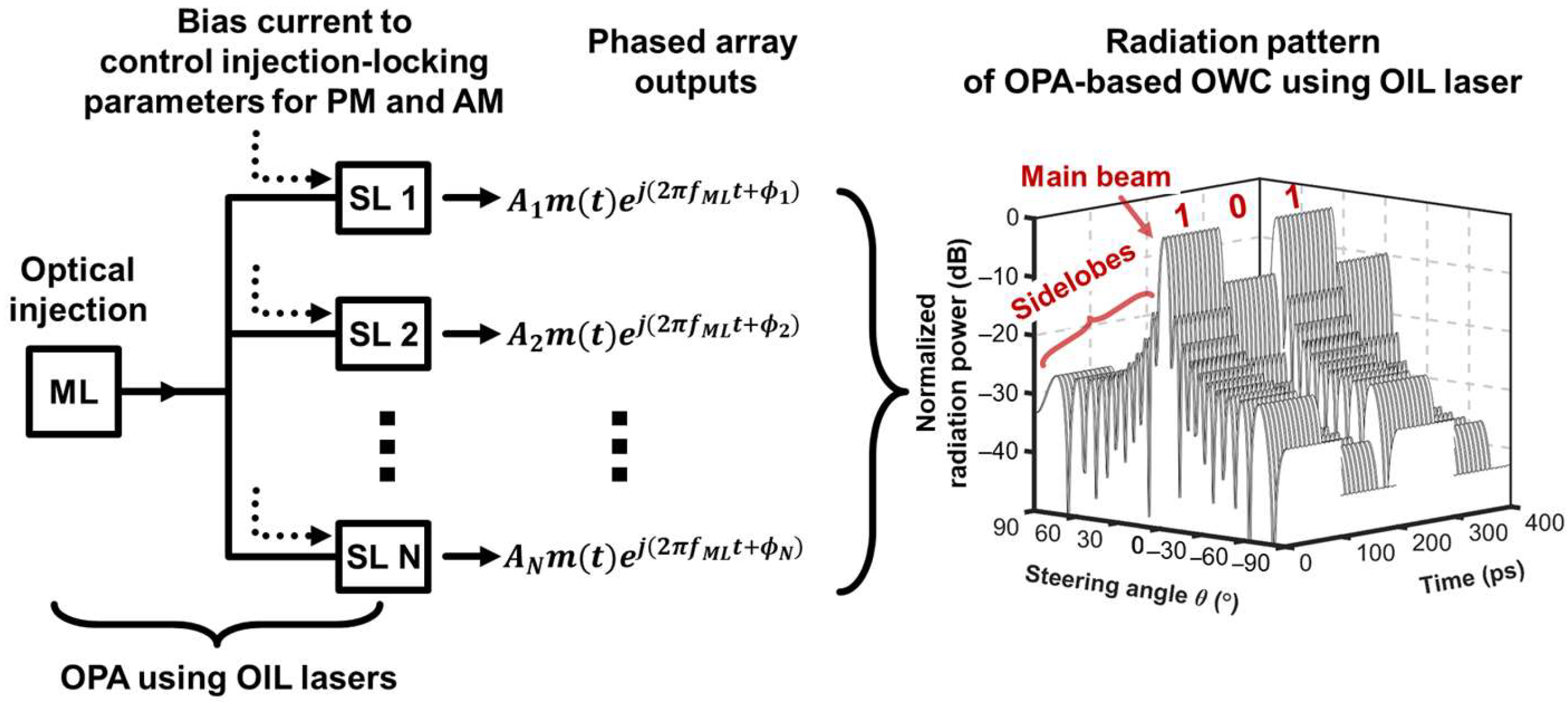
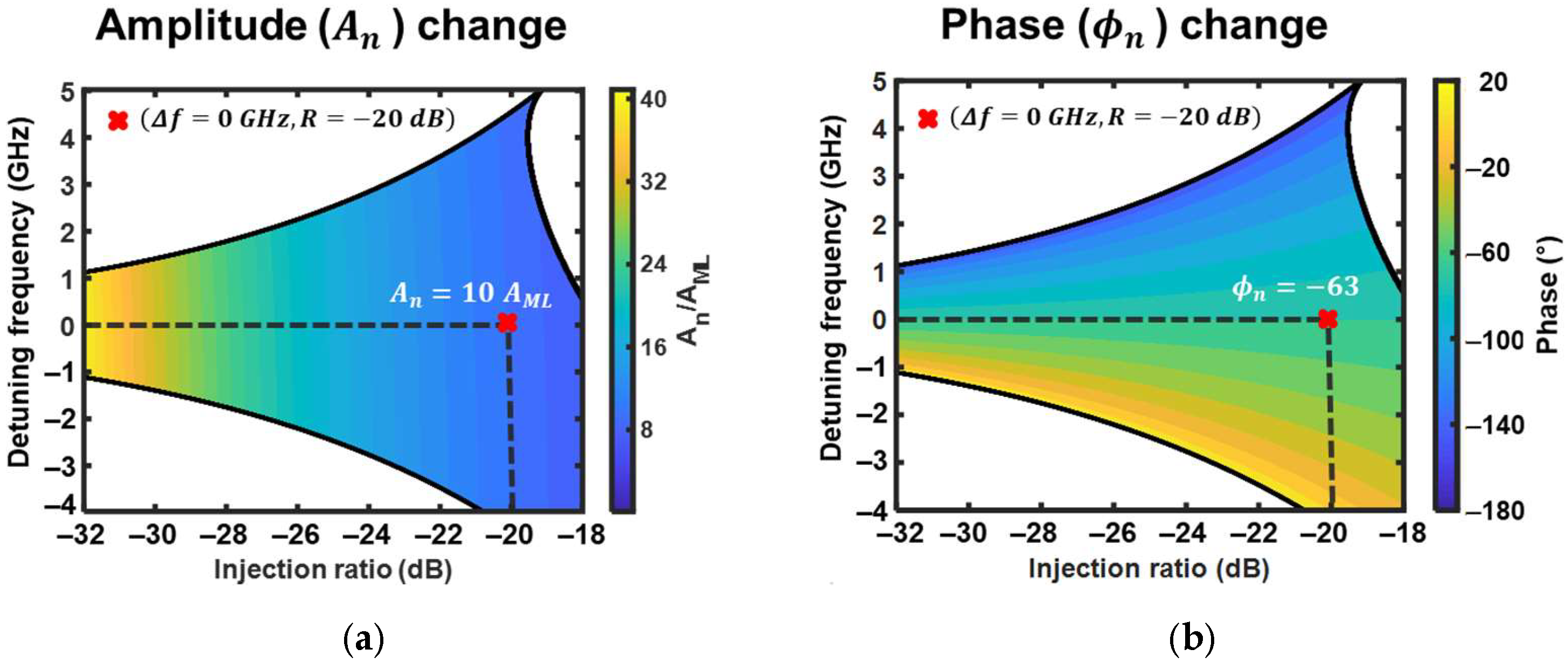
3. OPA Based on OIL Lasers
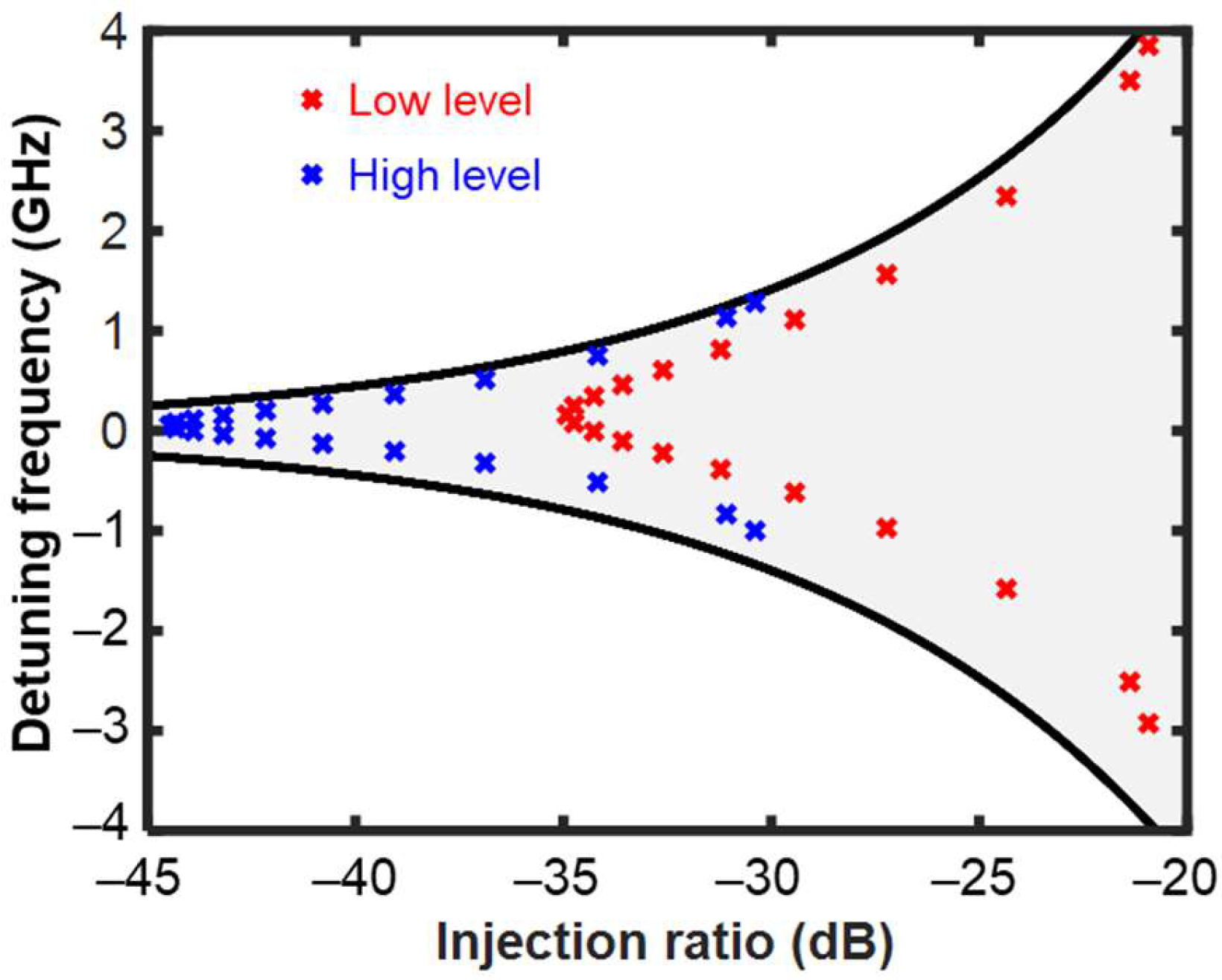
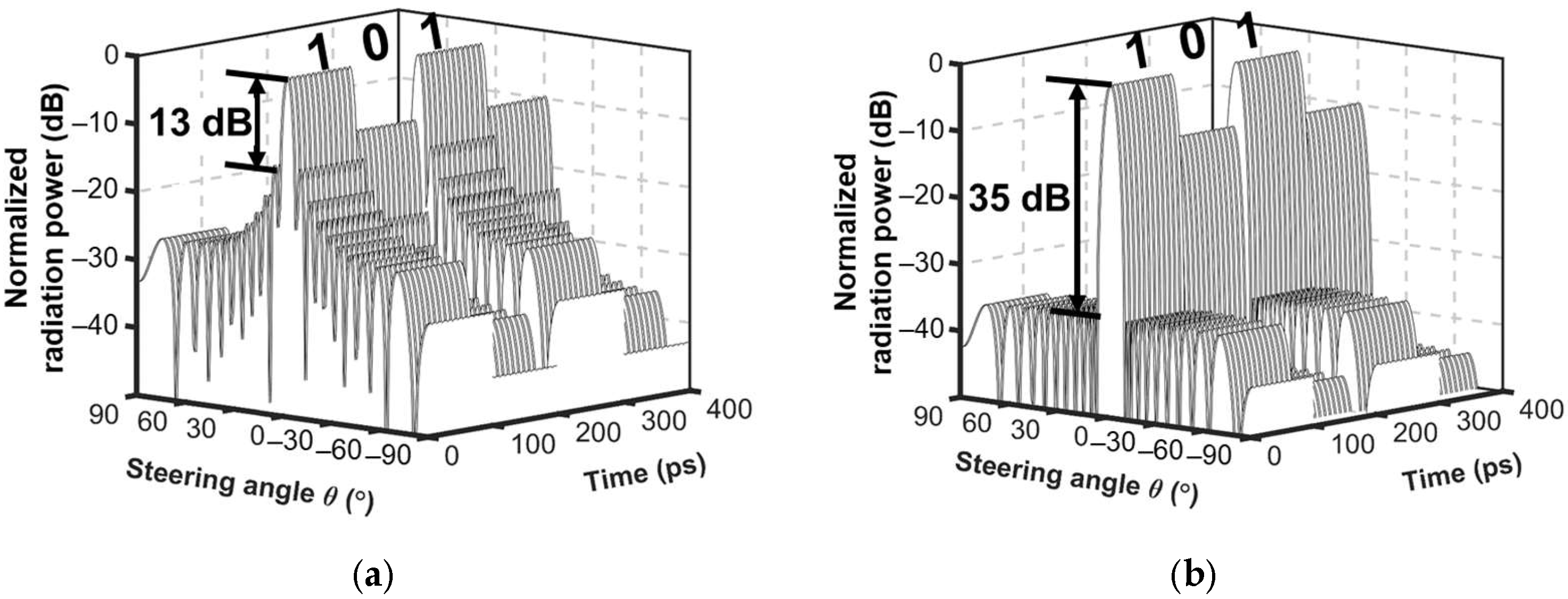
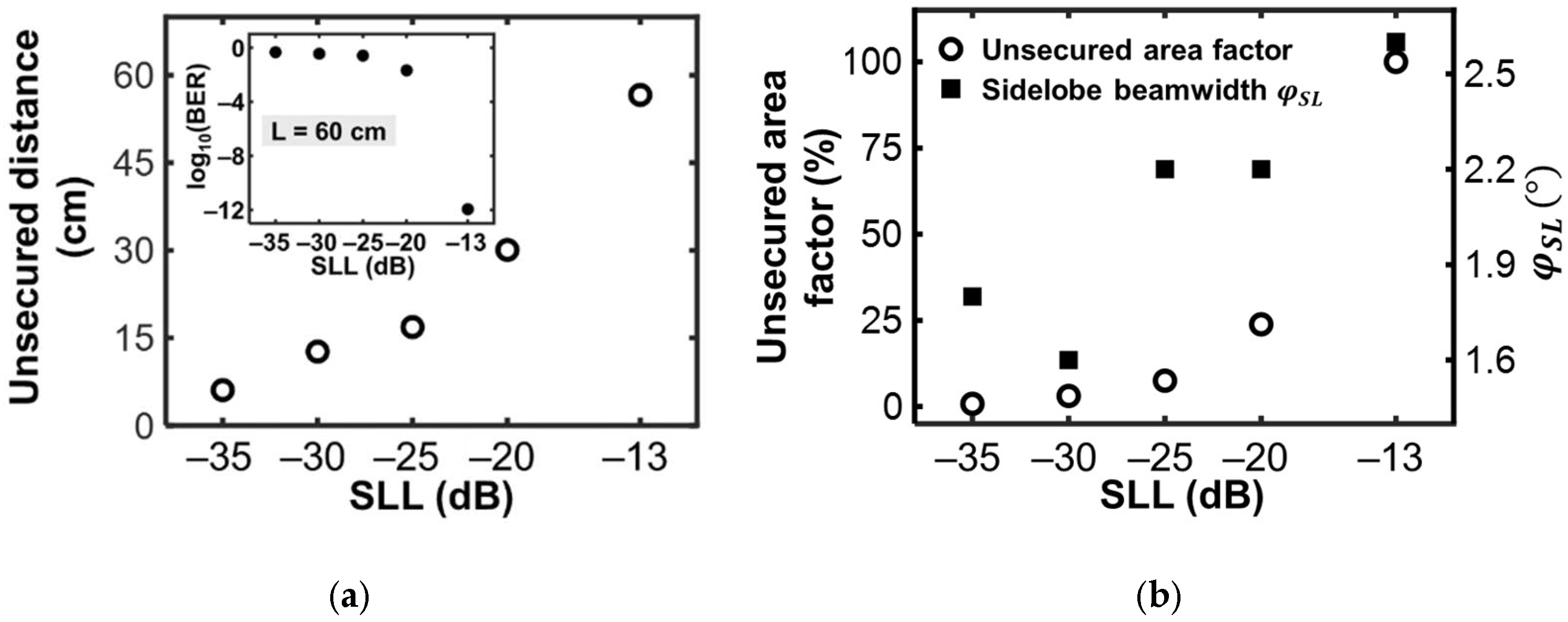
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uysal, M.; Capsoni, C.; Ghassemlooy, Z.; Boucouvalas, Z.; Udvary, A. Optical Wireless Communications, 1st ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 2–5. [Google Scholar]
- Karagiannidis, G.K.; Arnon, S.; Barry, J.R.; Schober, R.; Uysal, M. Guest editorial: Optical wireless communications. IEEE J. Sel. Areas Commun. 2009, 27, 1521–1525. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.; Hossan, M.T.; Islam, A.; Jang, Y.M. A comparative survey of optical wireless technologies: Architectures and applications. IEEE Access 2018, 6, 9819–9840. [Google Scholar] [CrossRef]
- Mahdy, A.; Deogun, J.S. Wireless Optical Communications: A Survey. In Proceedings of the IEEE Wireless Communications and Networking Conference, Atlanta, GA, USA, 21–25 March 2004. [Google Scholar]
- Uysal, M.; Nouri, H. Optical Wireless Communications—An Emerging Technology. In Proceedings of the 16th International Conference on Transparent Optical Networks (ICTON), Graz, Austria, 6–10 July 2014. [Google Scholar]
- Harald, H.; Jaafar, E.; Ian, W. Optical wireless communication. Philos. Trans. R. Soc. A 2020, 378, 1–11. [Google Scholar]
- Malik, A.; Singh, P. Free space optics: Current applications and future challenges. Int. J. Opt. 2015, 2015, 945483. [Google Scholar] [CrossRef] [Green Version]
- Gursale, V.M.; Patil, S.S.; Kakade, A.B. Enhancement in free space optical communication: A review. IJARCCE 2016, 5, 65–71. [Google Scholar]
- Hranilovic, S. Wireless Optical Communication Systems, 1st ed.; Springer: New York, NY, USA, 2005; pp. 3–8. [Google Scholar]
- Zhang, Z.; Dang, J.; Wu, L.; Wang, H.; Xia, J.; Lei, W.; Wang, J.; You, X. Optical mobile communications: Principles, implementation, and performance analysis. IEEE Trans. Veh. Technol. 2019, 68, 471–482. [Google Scholar] [CrossRef]
- Heck, M.J.R. Highly integrated optical phased arrays: Photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 1, 93–107. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-range LiDAR and free-space data communication with high-performance optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–8. [Google Scholar] [CrossRef]
- He, J.; Dong, T.; Xu, Y. Review of Photonic Integrated Optical Phased Arrays for Space Optical Communication. IEEE Access 2020, 8, 188284–188298. [Google Scholar] [CrossRef]
- Zang, H.; Zang, Z.; Lv, J.; Peng, C.; Hu, W. Fast beam steering enabled by a chip-scale optical phased array with 8 × 8 elements. Opt. Commun. 2020, 461, 12567. [Google Scholar]
- Gozzard, D.R.; Roberts, L.E.; Spollard, J.T.; Sibley, P.G.; Shaddock, D.A. Fast beam steering with an optical phased array. Opt. Lett. 2020, 45, 3793–3796. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, A.; Kwong, D.; Chen, R.T. Wide steering angle optical phased array based on silicon nano-membrane. In Photonics Packaging, Integration, and Interconnects IX, Proceedings of the SPIE: Integrated Optoelectronic Devices, San Joe, CA, USA, 12 February 2009; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; Volume 7221, p. 72210T. [Google Scholar]
- Roberts, L.E.; Ward, R.L.; Francis, S.P.; Sibley, P.G.; Fleddermann, R.; Sutton, A.J.; Smith, C.; McClelland, D.E.; Shaddock, D.A. High power compatible internally sensed optical phased array. Opt. Express 2016, 24, 13467–13479. [Google Scholar] [CrossRef]
- Huang, W.R.; Montoya, J.; Kansky, J.E.; Redmond, S.M.; Turner, G.W.; Sanchez-Rubio, A. High speed, high power one-dimensional beam steering from a 6-element optical phased array. Opt. Express 2012, 20, 17311–17318. [Google Scholar] [CrossRef] [PubMed]
- Roberts, L.E.; Ward, R.L.; Smith, C.; Shaddock, D.A. Coherent Beam Combining Using an Internally Sensed Optical Phased Array of Frequency-Offset Phase Locked Lasers. Photonics 2020, 7, 118. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, Y.; Li, C.; Zhang, H.; Zhou, X.; Zhang, L. Integrated Optical Phased Arrays for Beam Forming and Steering. Appl. Sci. 2021, 11, 4017. [Google Scholar] [CrossRef]
- Stulemeijer, J.; van Vliet, F.E.; Benoist, K.W.; Maat, D.H.P.; Smit, M.K. Compact photonic integrated phase and amplitude controller for phased-array antennas. IEEE Photonics Technol. Lett. 1999, 11, 122–124. [Google Scholar] [CrossRef] [Green Version]
- Sayyah, K.; Efimov, O.; Patterson, P.; Schffner, J.H. Two-dimensional pseudo-random optical phased array based on tandem optical injection locking of vertical cavity surface emitting lasers. Opt. Express 2015, 23, 19405–19416. [Google Scholar] [CrossRef]
- Abedasl, H.; Hashemi, H. Monolithic optical phased-array transceiver in a standard SOI CMOS process. Opt. Express 2015, 23, 6509–6519. [Google Scholar] [CrossRef]
- Sabouri, S.; Jamshidi, K. Design considerations of silicon nitride optical phased array for visible light communications. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–7. [Google Scholar] [CrossRef]
- Doylend, J.K.; Heck, M.J.R.; Bovington, J.T.; Peters, J.D.; Coldren, L.A.; Bowers, J.E. Two-dimensional free-space beam steering with an optical phased array on silicon-on-insulator. Opt. Express 2011, 19, 21595–21604. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Ju, Y.; Wang, B.; Cryan, J.; Zhao, B.Y.; Zheng, H. Wireless side-lobe eavesdropping attacks. arXiv 2018, arXiv:1810.10157. [Google Scholar]
- Balakrishnan, S.; Wang, P.; Bhuyan, A.; Sun, Z. Modeling and analysis of eavesdropping attack in 802.11ad mmWave wireless networks. IEEE Access 2019, 7, 70355–70370. [Google Scholar] [CrossRef]
- Hong, Y.; Jing, X.; Gao, H.; He, Y. Fixed region beamforming using frequency diverse subarray for secure mmWave wireless communications. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2706–2721. [Google Scholar] [CrossRef]
- Kwong, D.; Hosseini, A.; Zhang, Y.; Chen, R.T. 1 × 12 Unequally spaced waveguide array for actively tuned optical phased array on a silicon nanomembrane. Appl. Phys. Lett. 2011, 99, 51104. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Hosseini, E.S.; Yaacobi, A.; Cole, D.B.; Leake, G.; Coolbaugh, D.; Watts, M.R. Two-dimensional apodized silicon photonic phased arrays. Opt. Lett. 2014, 39, 367–370. [Google Scholar] [CrossRef]
- Dregely, D.; Taubert, R.; Dorfmuller, J.; Vogelgesang, R.; Kern, K.; Giessen, H. 3D optical Yagi–Uda nanoantenna array. Nat. Commun. 2011, 2, 267. [Google Scholar] [CrossRef] [Green Version]
- Yifat, Y.; Eitan, M.; Lluz, Z.; Hanein, Y.; Boag, A.; Scheuer, J. Highly Efficient and Broadband Wide-Angle Holography Using Patch-Dipole Nanoantenna Reflectarrays. Nano Lett. 2014, 14, 2485–2490. [Google Scholar] [CrossRef] [Green Version]
- Cho, J.H.; Cho, C.H.; Sung, H.K. Theoretical performance evaluation of optical complex signals based on optically injection-locked semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–9. [Google Scholar] [CrossRef]
- Lau, E.K.; Wong, L.J.; Wu, M.C. Enhanced modulation characteristics of optical injection-locked lasers: A tutorial. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 618–633. [Google Scholar] [CrossRef]
- Lucente, M.; Kintzer, E.S.; Alexander, S.B.; Fujimoto, J.G.; Chan, V.W. Coherent Optical Communication with an Injection-Locked High Power Diode Laser Array. In Proceedings of the Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 24 April 1989. [Google Scholar]
- Ying, C.L.; Lu, H.H.; Li, C.Y.; Cheng, C.J.; Peng, P.C.; Ho, W.J. 20-Gbps optical LiFi transport system. Opt. Lett. 2015, 40, 3276–3279. [Google Scholar] [CrossRef]
- Hasebe, K.; Koyama, F. All-optical signal processing based on optical injection-locked two-mode vertical-cavity surface-emitting laser. In Physics and Simulation of Optoelectronic Devices XIV, Proceedings of the SPIE: Integrated Optoelectronic Devices 2006, San Joe, CA, USA, 28 February 2006; International Society for Optics and Photonics: Bellingham, WA, USA, 2006; Volume 6115. [Google Scholar]
- Goldberg, L.; Taylor, H.F.; Weller, J.F.; Bloom, D.M. Microwave signal generation with injection locked laser diodes. Electron. Lett. 1983, 19, 491–493. [Google Scholar] [CrossRef]
- Keiser, G. Optical Fiber Communications, 5th ed.; McGraw Hill: Singapore, 2015; pp. 267–308. [Google Scholar]
- Dai, H.; Li, D.; Wong, R.C. Exploring Security Improvement of Wireless Networks with Directional Antennas. In Proceedings of the IEEE 36th Conference on Local Computer Networks, Bonn, Germany, 4–7 October 2011. [Google Scholar]
- Nguyen, A.H.; Cho, J.H.; Bae, H.J.; Sung, H.K. Side-lobe level reduction of an optical phased array using amplitude and phase modulation of array elements based on optically injection-locked semiconductor lasers. Photonics 2020, 20, 20. [Google Scholar] [CrossRef] [Green Version]
- Mogensen, F.; Olesen, H.; Jacobsen, G. Locking conditions and stability properties for a semiconductor laser with external light injection. IEEE J. Quantum Electron. 1985, 21, 784–793. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, A.-H.; Cho, J.-H.; Sung, H.-K. Theoretical Demonstration of Security Improvement of Optical Phased Array Based on Optically Injection-Locked Lasers. Photonics 2021, 8, 469. https://doi.org/10.3390/photonics8110469
Nguyen A-H, Cho J-H, Sung H-K. Theoretical Demonstration of Security Improvement of Optical Phased Array Based on Optically Injection-Locked Lasers. Photonics. 2021; 8(11):469. https://doi.org/10.3390/photonics8110469
Chicago/Turabian StyleNguyen, Anh-Hang, Jun-Hyung Cho, and Hyuk-Kee Sung. 2021. "Theoretical Demonstration of Security Improvement of Optical Phased Array Based on Optically Injection-Locked Lasers" Photonics 8, no. 11: 469. https://doi.org/10.3390/photonics8110469
APA StyleNguyen, A. -H., Cho, J. -H., & Sung, H. -K. (2021). Theoretical Demonstration of Security Improvement of Optical Phased Array Based on Optically Injection-Locked Lasers. Photonics, 8(11), 469. https://doi.org/10.3390/photonics8110469





