A Metasurface Beam Combiner Based on the Control of Angular Response
Abstract
:1. Introduction
2. Design and Results
2.1. Gradient Metasurface for Beam Combining
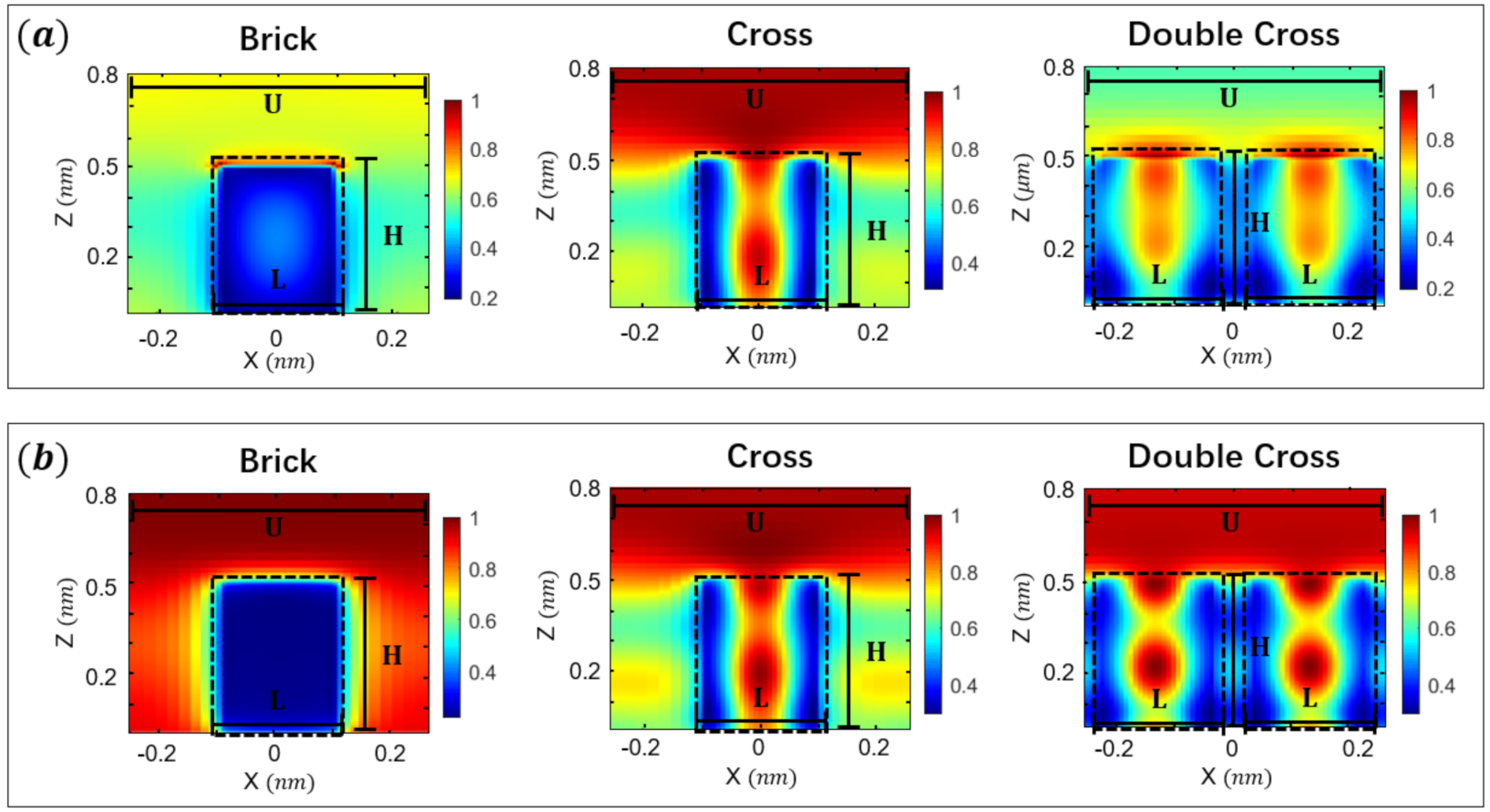
2.2. Angle-Sensitive Unitcell Design
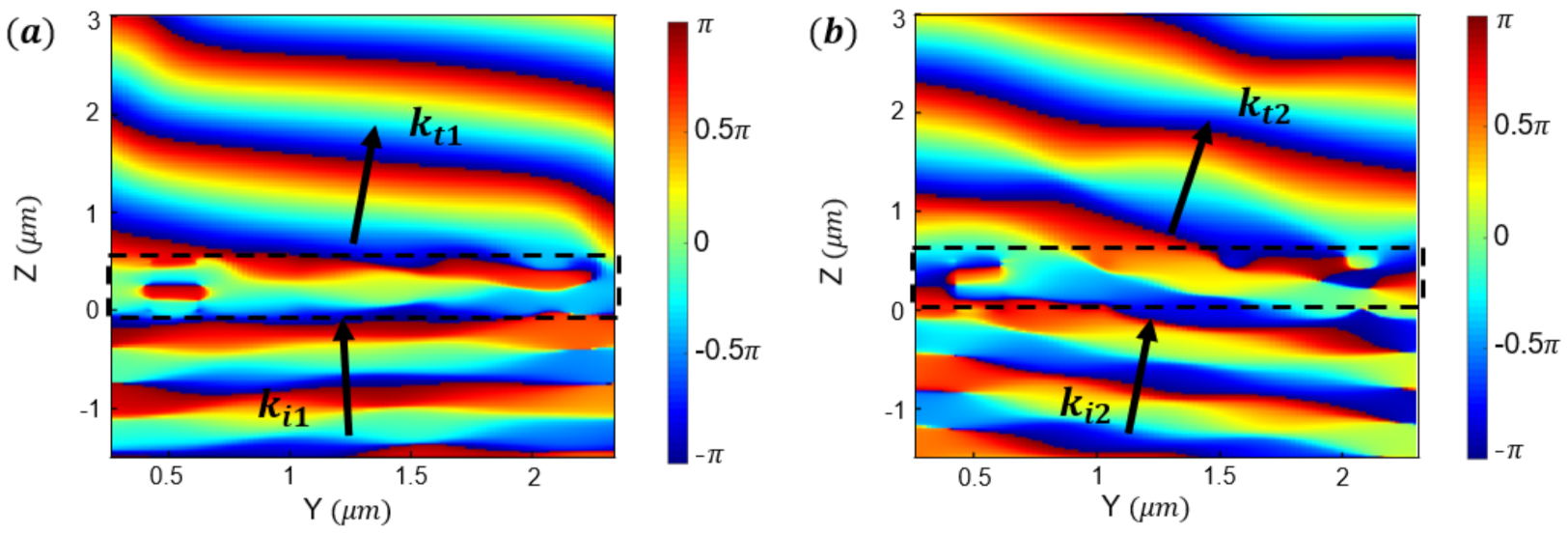
2.3. Metasurface Beam Combiner
3. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Daneu, V.; Sanchez, A.; Fan, T.Y.; Choi, H.K.; Turner, G.W.; Cook, C.C. Spectral beam combining of a broad-stripe diode laser array in an external cavity. Opt. Lett. 2000, 25, 405–407. [Google Scholar] [CrossRef] [PubMed]
- Augst, S.J.; Ranka, J.K.; Fan, T.Y.; Sanchez, A. Beam combining of ytterbium fiber amplifiers (Invited). J. Opt. Soc. Am. B 2007, 24, 1707–1715. [Google Scholar] [CrossRef]
- Jin, Y.Y.; Zou, Y.G.; Ma, X.H.; Li, J.; Li, Y.; Jin, L.; Xu, L.; Zhao, W.; Sui, Q.X.; Zhang, Z.W. Study on laser diode incoherent beam combining technology based on tracepro. In Proceedings of the International Conference on Optoelectronics & Microelectronics (ICOM), Changchun, China, 23–25 August 2012; pp. 87–90. [Google Scholar]
- Fan, T.Y. Laser beam combining for high-power, high-radiance sources. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 567–577. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, Z.J.; Wang, X.L.; Ma, Y.X.; Ma, H.T.; Xu, X.J. Coherent beam combination of two-dimensional high-power fiber amplifier array using stochastic parallel gradient descent algorithm. Appl. Phys. Lett. 2009, 94, 231106. [Google Scholar] [CrossRef]
- Bourderionnet, J.; Bellanger, C.; Primot, J.; Brignon, A. Collective coherent phase combining of 64 fibers. Opt. Express 2011, 19, 17053–17058. [Google Scholar] [CrossRef] [PubMed]
- Su, R.T.; Xi, J.C.; Chang, H.X.; Ma, Y.X.; Ma, P.F.; Wu, J.; Jiang, M.; Zhou, P.; Si, L.; Xu, X.J.; et al. Coherent combining of 60 fiber lasers using stochastic parallel gradient descent algorithm. In Proceedings of the Applications of Lasers for Sensing and Free Space Communications, Vienna, Austria, 29 September–3 October 2019; p. JW2A-1. [Google Scholar] [CrossRef]
- Yu, C.X.; Augst, S.J.; Redmond, S.M.; Goldizen, K.C.; Murphy, D.V.; Sanchez, A.; Fa, T.Y. Coherent combining of a 4 kW, eight-element fiber amplifier array. Opt. Lett. 2011, 36, 2686–2688. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.X.; Chang, Q.; Xi, J.C.; Hou, T.Y.; Su, R.T.; Ma, P.F.; Wu, J.; Li, C.; Jiang, M.; Ma, Y.X.; et al. First experimental demonstration of coherent beam combining of more than 100 beams. Photonics Res. 2020, 8, 1943–1948. [Google Scholar] [CrossRef]
- Flores, A.; Ehrenreich, T.; Holten, R.; Anderson, B.; Dajani, I. Multi-kW coherent combining of fiber lasers seeded with pseudo random phase modulated light. Proc. SPIE 2016, 9728, 97281Y. [Google Scholar]
- Lin, D.M.; Fan, P.Y.; Hasman, E.; Brongersma, M.L. Dielectric gradient metasurface optical elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef]
- Lio, G.E.; Ferraro, A.; Ritacco, T.; Aceti, D.M.; De Luca, A.; Giocondo, M.; Caputo, R. Leveraging on ENZ Metamaterials to Achieve 2D and 3D Hyper-Resolution in Two-Photon Direct Laser Writing. Adv. Mater. 2021, 33, 2008644. [Google Scholar] [CrossRef]
- Sun, Q.; Liang, H.W.; Zhang, J.C.; Feng, W.B.; Martins, E.R.; Krauss, T.F.; Li, J.T. Highly efficient air-mode silicon metasurfaces for visible light operation embedded in a protective silica layer. Adv. Opt. Mater. 2021, 9, 2002209. [Google Scholar] [CrossRef]
- Yu, N.F.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.H.; Wu, P.C.; Su, V.C.; Lai, Y.C.; Chu, C.H.; Lee, I.C.; Chen, J.W.; Chen, Y.H.; Lan, Y.C.; Kuan, C.H.; et al. GaN metalens for pixel-level full-color routing at visible light. Nano Lett. 2017, 17, 6345–6352. [Google Scholar] [CrossRef]
- Avayu, O.; Almeida, E.; Prior, Y.; Ellenbogen, T. Composite functional metasurfaces for multispectral achromatic optics. Nat. Commun. 2017, 8, 14992. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Arbabi, E.; Kamali, S.M.; Horie, Y.; Han, S.; Faraon, A. Miniature optical planar camera based on a wide-angle metasurface doublet corrected for monochromatic aberrations. Nat. Commun. 2016, 7, 13682. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Sultana, J.; Biabanifard, M.; Vafapour, Z.; Nine, M.J.; Dinovitser, A.; Cordeiro, C.M.B.; Ng, B.W.H.; Abbott, D. Tunable localized surface plasmon graphene metasurface for multiband superabsorption and terahertz sensing. Carbon 2020, 158, 559–567. [Google Scholar] [CrossRef]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; de Abajo, F.J.G.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, G.X.; Muhlenbernd, H.; Kenney, M.; Li, G.X.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Burch, J.; Wen, D.D.; Chen, X.Z.; Di Falco, A. Conformable holographic metasurfaces. Sci. Rep. 2017, 7, 4520. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.M.; Wang, W.Y.; Boulesbaa, A.; Kravchenko, I.I.; Briggs, D.P.; Puretzky, A.; Geohegan, D.; Valentine, J. Nonlinear fano-resonant dielectric metasurfaces. Nano Lett. 2015, 15, 7388–7393. [Google Scholar] [CrossRef] [PubMed]
- Chervinskii, S.; Koskinen, K.; Scherbak, S.; Kauranen, M.; Lipovskii, A. Nonresonant local fields enhance second-harmonic generation from metal nanoislands with dielectric cover. Phys. Rev. Lett. 2018, 120, 113902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Z.P.; Li, J.T.; Su, R.B.; Yao, B.M.; Fang, H.L.; Li, K.Z.; Zhou, L.D.; Liu, J.; Stellinga, D.; Reardon, C.P.; et al. Efficient silicon metasurfaces for visible light. ACS Photonics 2017, 4, 544–551. [Google Scholar] [CrossRef]
- Martins, A.; Li, K.Z.; Li, J.T.; Liang, H.W.; Conteduca, D.; Borges, B.V.; Krauss, T.F.; Martins, E.R. On metalenses with arbitrarily wide field of view. ACS Photonics 2020, 7, 2073–2079. [Google Scholar] [CrossRef]
- Chen, K.; Ding, G.W.; Hu, G.W.; Jin, Z.W.; Zhao, J.M.; Feng, Y.J.; Jiang, T.; Alu, A.; Qiu, C.W. Directional janus metasurface. Adv. Mater. 2020, 32, 1906352. [Google Scholar] [CrossRef] [PubMed]
- Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary spin-to-orbital angular momentum conversion of light. Science 2017, 358, 896–900. [Google Scholar] [CrossRef] [Green Version]
- Yu, N.F.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [Green Version]
- Aieta, F.; Kats, M.A.; Genevet, P.; Cappasso, F. Multiwavelength achromatic metasurfaces by dispersive phase compensation. Science 2015, 347, 1342–1345. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Tian, Z.; Yue, W.S.; Gu, J.Q.; Zhang, S.; Han, J.G.; Zhang, W.L. Broadband terahertz wave deflection based on C-shape complex metamaterials with phase discontinuities. Adv. Mater. 2013, 25, 4567–4572. [Google Scholar] [CrossRef]
- Yang, H.; Deng, Y. Broadband and high efficiency all-dielectric metasurfaces for wavefront steering with easily obtained phase shift. Opt. Commun. 2017, 405, 39–42. [Google Scholar] [CrossRef]
- Zhao, Y.; Alu, A. Manipulating light polarization with ultrathin plasmonic metasurfaces. Phys. Rev. B 2011, 84, 205428. [Google Scholar] [CrossRef]
- He, M.X.; Guo, Y.H.; Li, C.S.; Tong, X.; Liu, H.A.; Li, G.F.; Zhang, L. Metasurface-based wide-angle beam steering for optical trapping. IEEE Access 2020, 8, 37275–37280. [Google Scholar] [CrossRef]
- Komar, A.; Paniagua-Dominguez, R.; Miroshnichenko, A.; Yu, Y.F.; Kivshar, Y.S.; Kuznetsov, A.I.; Neshev, D. Dynamic beam switching by liquid crystal tunable dielectric metasurface. ACS Photonics 2018, 5, 1742–1748. [Google Scholar] [CrossRef] [Green Version]
- Lio, G.E.; Ferraro, A. LIDAR and beam steering tailored by neuromorphic metasurface dipped in a tunable surrounding medium. Photonics 2021, 8, 65. [Google Scholar] [CrossRef]
- Shirmanesh, G.K.; Sokhoyan, R.; Wu, P.C.; Atwater, H.A. Electro-optically tunable multifunctional metasurface. ACS Nano 2020, 14, 6912–6920. [Google Scholar] [CrossRef] [PubMed]
- Albero, J.; Davis, J.A.; Cottrell, D.M.; Granger, C.E.; McCormick, K.R.; Moreno, I. Generalized diffractive optical elements with asymmetric harmonic response and phase control. Appl. Opt. 2013, 52, 3637–3644. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.J.; Sell, D.; Fan, J.A. Freeform metagratings based on complex light scattering dynamic for extreme, high efficiency beam steering. Ann. Der. Phys. 2018, 530, 1700302. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.Y.; Zou, H.J.; Su, M.Y.; Tang, L.W.; Wang, C.F.; Chen, S.Q.; Su, C.L.; Li, Y. All-dielectric metasurface-based beam splitter with arbitrary splitting ratio. Nanomaterials 2021, 11, 1137. [Google Scholar] [CrossRef]
- Li, J.; Ye, H.; Wu, T.S.; Liu, Y.M.; Yu, Z.Y.; Wang, Y.; Sun, Y.H.; Yu, L. Ultra-broadband large-angle beam splitter based on a homogeneous metasurface at visible wavelengths. Opt. Express 2020, 28, 32226–32238. [Google Scholar] [CrossRef]
- Cheng, J.R.; Inampudi, S.; Mosallaei, H. Optimization-based dielectric metasurfaces for angle-selective multifunctional beam deflection. Sci. Rep. 2017, 7, 12228. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Asadchy, V.S.; Fan, S.; Tretyakov, S.A. Space-time metasurfaces for perfect power combining of waves. arXiv 2021, arXiv:2105.14627vl. [Google Scholar]
- Kamali, S.M.; Arbabi, A.; Arbabi, E.; Horie, Y.; Faraon, A. Decoupling optical function and geometrical form using conformal flexible dielectric metasurfaces. Nat. Commun. 2016, 7, 11618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jang, M.; Horie, Y.; Shibukawa, A.; Brake, J.; Liu, Y.; Kamali, S.M.; Arbabi, A.; Ruan, H.W.; Faraon, A.; Yang, C.H. Wavefront shaping with disorder-engineered metasurfaces. Nat. Photonics 2018, 12, 84–90. [Google Scholar] [CrossRef]
- Decker, M.; Chen, W.T.; Nobis, T.; Zhu, A.Y.; Khorasaninejad, M.; Bharwani, Z.; Capasso, F.; Petschulat, J. Imaging performance of polarization-insensitive metalenses. ACS Photonics 2019, 6, 1493–1499. [Google Scholar] [CrossRef]
- Kalvach, A.; Szabo, Z. Aberration-free flat lens design for a wide range of incident angles. J. Opt. Soc. Am. B 2016, 33, A66–A71. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Lin, L.; Ma, D.; Yun, S.; Werner, D.H.; Liu, Z.W.; Mayer, T.S. Broadband and wide field-of-view plasmonic metasurface-enabled waveplates. Sci. Rep. 2014, 4, 7511. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Y.; Li, Q.; Liu, F.F.; Qiu, M.; Sun, S.L.; He, Q.; Zhou, L. Controlling angular dispersions in optical metasurfaces. Light Sci. Appl. 2020, 9, 76. [Google Scholar] [CrossRef] [PubMed]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Horie, Y.; Faraji-Dana, M.; Faraon, A. Angle-multiplexed metasurfaces: Encoding independent wavefronts in a single metasurface under different illumination angles. Phys. Rev. X 2017, 7, 041056. [Google Scholar] [CrossRef] [Green Version]
- Aoni, R.A.; Rahmani, M.; Xu, L.; Kamali, K.Z.; Komar, A.; Yen, J.S.; Neshev, D.; Miroshnichenko, A.E. High-efficiency visible light manipulation using dielectric metasurface. Sci. Rep. 2019, 9, 6510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asadchy, V.S.; Diaz-Rubio, A.; Tcvetkova, S.N.; Kwon, D.H.; Elsakka, A.; Albooyeh, M.; Tretyakov, S.A. Flat engineered multichannel reflectors. Phys. Rev. X 2017, 7, 031046. [Google Scholar] [CrossRef]
- Snell, D.; Yang, J.J.; Doshay, S.; Yang, R.; Fan, J.A. Large-angle, multifunctional metagrating based on freeform multimode geometries. Nano Lett. 2017, 17, 3752–3757. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Feng, W.; Long, Y.; Guo, S.; Liang, H.; Qiu, Z.; Fu, X.; Li, J. A Metasurface Beam Combiner Based on the Control of Angular Response. Photonics 2021, 8, 489. https://doi.org/10.3390/photonics8110489
Liu Z, Feng W, Long Y, Guo S, Liang H, Qiu Z, Fu X, Li J. A Metasurface Beam Combiner Based on the Control of Angular Response. Photonics. 2021; 8(11):489. https://doi.org/10.3390/photonics8110489
Chicago/Turabian StyleLiu, Zhihao, Weibin Feng, Yong Long, Songming Guo, Haowen Liang, Zhiren Qiu, Xiao Fu, and Juntao Li. 2021. "A Metasurface Beam Combiner Based on the Control of Angular Response" Photonics 8, no. 11: 489. https://doi.org/10.3390/photonics8110489
APA StyleLiu, Z., Feng, W., Long, Y., Guo, S., Liang, H., Qiu, Z., Fu, X., & Li, J. (2021). A Metasurface Beam Combiner Based on the Control of Angular Response. Photonics, 8(11), 489. https://doi.org/10.3390/photonics8110489




