In-Situ Depth Measurement of Laser Micromachining
Abstract
:1. Introduction
2. Materials and Methods
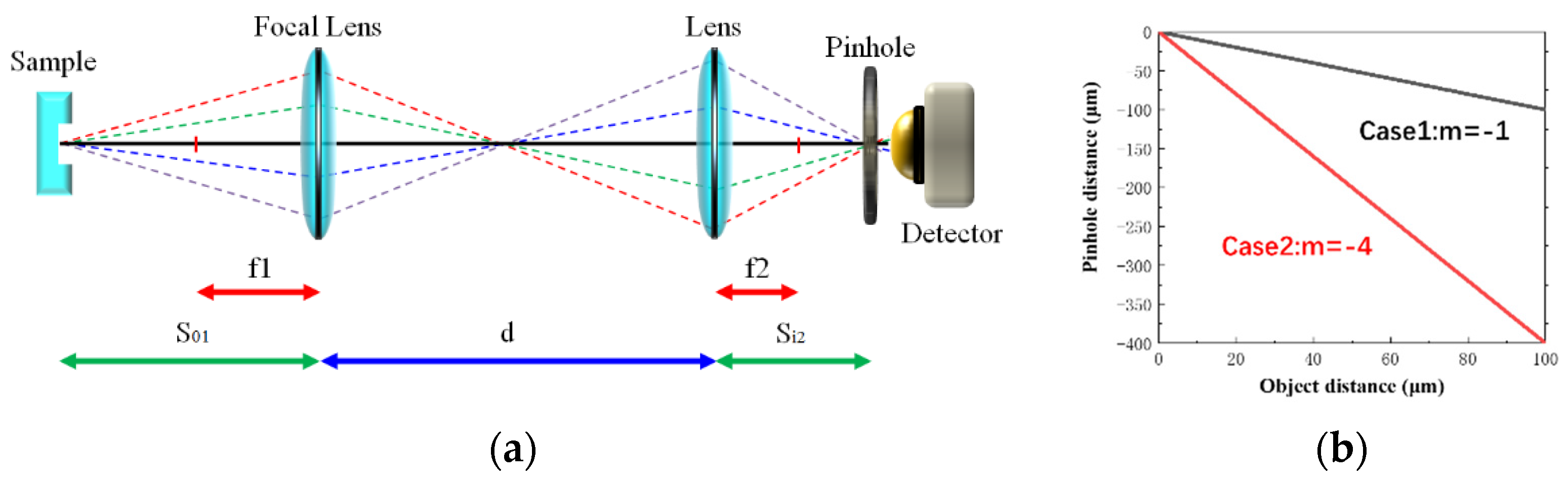
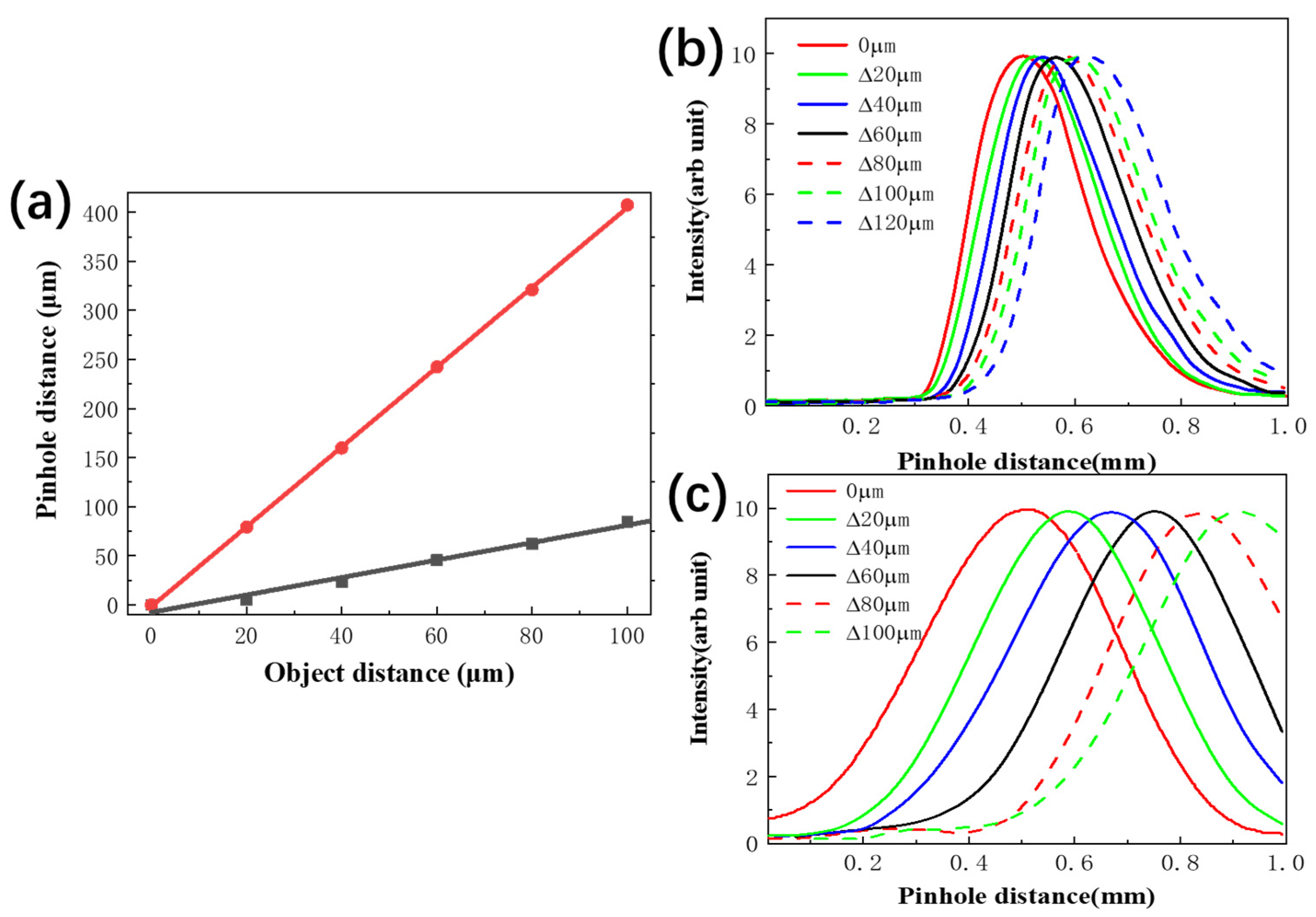
3. Theoretical Model Using Numerical Simulation
4. Results and Discussion
4.1. Confocal System Tested Using Polished Stainless Steel
4.2. The Designed Experiments for Laser Drilling in Aluminum Alloy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Petkovsek, R.; Panjan, I.; Babnik, A.; Mozina, J. Optodynamic study of multiple pulses micro drilling. Ultrasonics 2006, 44, E1191–E1194. [Google Scholar] [CrossRef]
- Yeack, C.E.; Melcher, R.L.; Klauser, H.E. Transient photo-acoustic monitoring of pulsed laser drilling. Appl. Phys. Lett. 1982, 41, 1043–1044. [Google Scholar] [CrossRef]
- Strgar, S.; Mozina, J. An optodynamic determination of the depth of laser-drilled holes by the simultaneous detection of ultrasonic waves in the air and in the workpiece. Ultrasonics 2002, 40, 791–795. [Google Scholar] [CrossRef]
- Stafe, M.; Negutu, C.; Popescu, I.M. Real-time determination and controlof the laser-drilled holes depth. Shock Waves 2005, 14, 123–126. [Google Scholar] [CrossRef]
- Petkovsek, R.; Babnik, A.; Diaci, J.; Mozina, J. Optodynamic monitoring of laser micro-drilling of glass by using a laser probe. Appl. Phys. A-Mater. Sci. Process. 2008, 93, 141–145. [Google Scholar] [CrossRef]
- Idris, N.; Madjid, S.N.; Ramli, M.; Kurniawan, K.H.; Lee, Y.I.; Kagawa, K. Monitoring of laser processing using induced current under applied electric field on laser produced-plasma. J. Mater. Process. Technol. 2009, 209, 3009–3021. [Google Scholar] [CrossRef]
- Papazoglou, D.G.; Papadakis, V.; Anglos, D. In situ interferometric depth and topography monitoring in LIBS elemental profiling of multi-layer structures. J. Anal. At. Spectrom. 2004, 19, 483–488. [Google Scholar] [CrossRef]
- Ruiz, J.; González, A.; Cabalín, L.M.; Laserna, J.J. On-Line Laser-Induced Breakdown Spectroscopy Determination of Magnesium Coating Thickness on Electrolytically Galvanized Steel in Motion. Appl. Spectrosc. 2010, 64, 1342–1349. [Google Scholar] [CrossRef]
- Rhee, H.G.; Kim, D.I.; Lee, Y.W. Realization and performance evaluation of high speed autofocusing for direct laser lithography. Rev. Sci. Instrum. 2009, 80, 073103. [Google Scholar] [CrossRef]
- Lading, L.; DamHansen, C.; Rasmussen, E. Surface light scattering: Integrated technology and signal processing. Appl. Opt. 1997, 36, 7593–7600. [Google Scholar] [CrossRef]
- Hofstetter, D.; Zappe, H.P.; Dandliker, R. Optical displacement measurement with GaAs/AlCaAs-based monolithically integrated Michelson interferometers. J. Lightwave Technol. 1997, 15, 663–670. [Google Scholar] [CrossRef]
- Webb, R.H. Confocal optical microscopy. Rep. Prog. Phys. 1996, 59, 427–471. [Google Scholar] [CrossRef]
- Arons, E.; Leith, E. Coherence confocal-imaging system for enhanced depth discrimination in transmitted light. Appl. Opt. 1996, 35, 2499–2506. [Google Scholar] [CrossRef] [PubMed]
- Minsky, M. Memoir on inventing the confocal scanning microscope. Scanning 1988, 10, 128–138. [Google Scholar] [CrossRef]
- Paddock, S. Over the rainbow: 25 years of confocal imaging. Biotechniques 2008, 44, 643–648. [Google Scholar] [CrossRef]
- Tan, B. Deep micro hole drilling in a silicon substrate using multi-bursts of nanosecond UV laser pulses. J. Micromech. Microeng. 2006, 16, 109–112. [Google Scholar] [CrossRef]

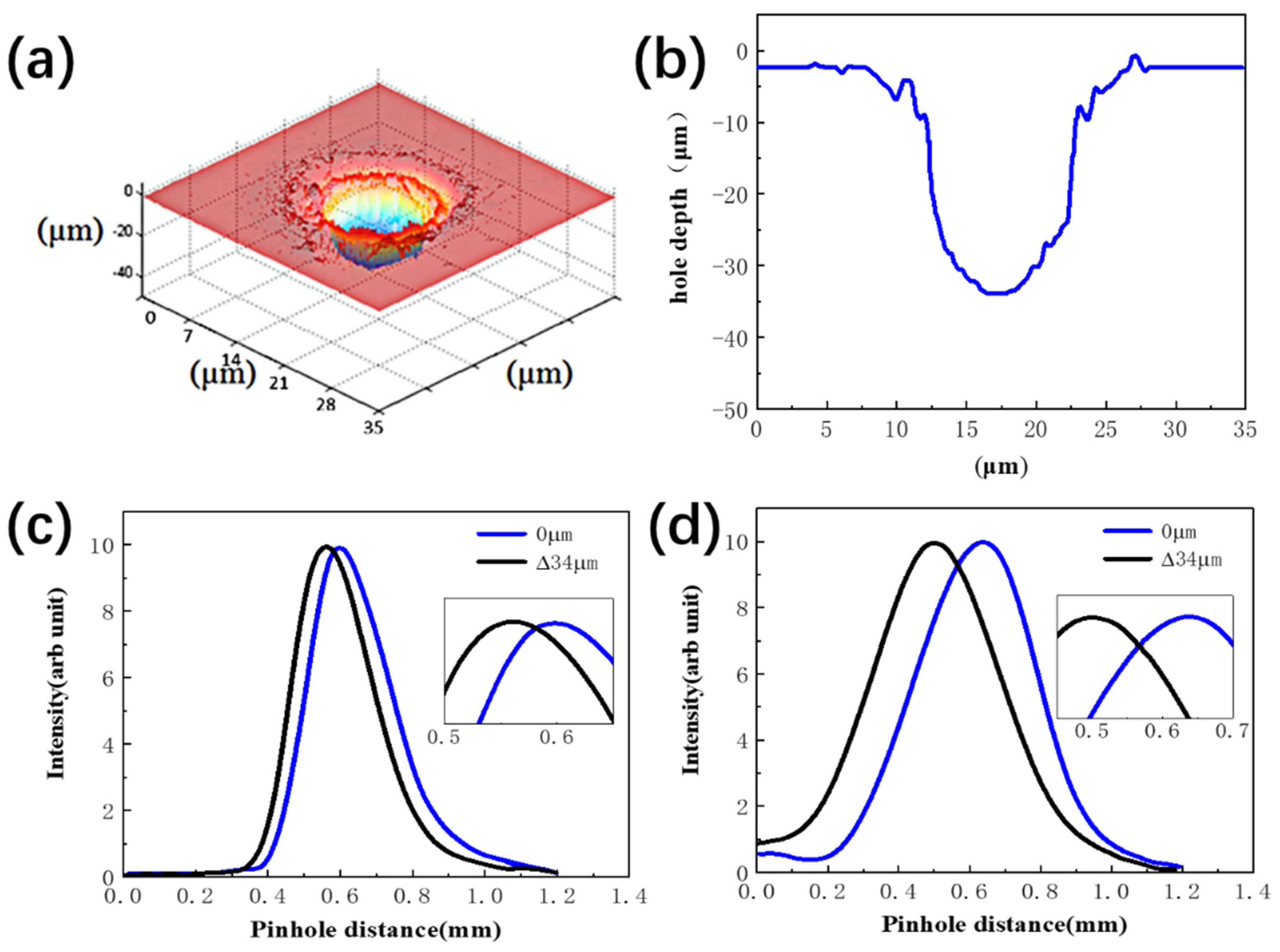


| Number of Laser Pulses | Hole Depth and Error (Unit: µm (%)) | ||
|---|---|---|---|
| 3D Laser Microscope | Case 1 | Case 2 | |
| 20 | 34.04 | 35 (2.94%) | 33.75 (0.85%) |
| 40 | 44.81 | 45 (0.44%) | 45.5 (1.56%) |
| 60 | 51.15 | 50.4 (1.37%) | 53 (3.71%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Xu, Y.; Chen, N.-K.; Shy, S.; Chui, H.-C. In-Situ Depth Measurement of Laser Micromachining. Photonics 2021, 8, 493. https://doi.org/10.3390/photonics8110493
Chen X, Xu Y, Chen N-K, Shy S, Chui H-C. In-Situ Depth Measurement of Laser Micromachining. Photonics. 2021; 8(11):493. https://doi.org/10.3390/photonics8110493
Chicago/Turabian StyleChen, Xiaoming, Ying Xu, Nan-Kuang Chen, Shannon Shy, and Hsiang-Chen Chui. 2021. "In-Situ Depth Measurement of Laser Micromachining" Photonics 8, no. 11: 493. https://doi.org/10.3390/photonics8110493
APA StyleChen, X., Xu, Y., Chen, N. -K., Shy, S., & Chui, H. -C. (2021). In-Situ Depth Measurement of Laser Micromachining. Photonics, 8(11), 493. https://doi.org/10.3390/photonics8110493





