Ultra-Compact Power Splitters with Low Loss in Arbitrary Direction Based on Inverse Design Method
Abstract
:1. Introduction
2. Methods and Results
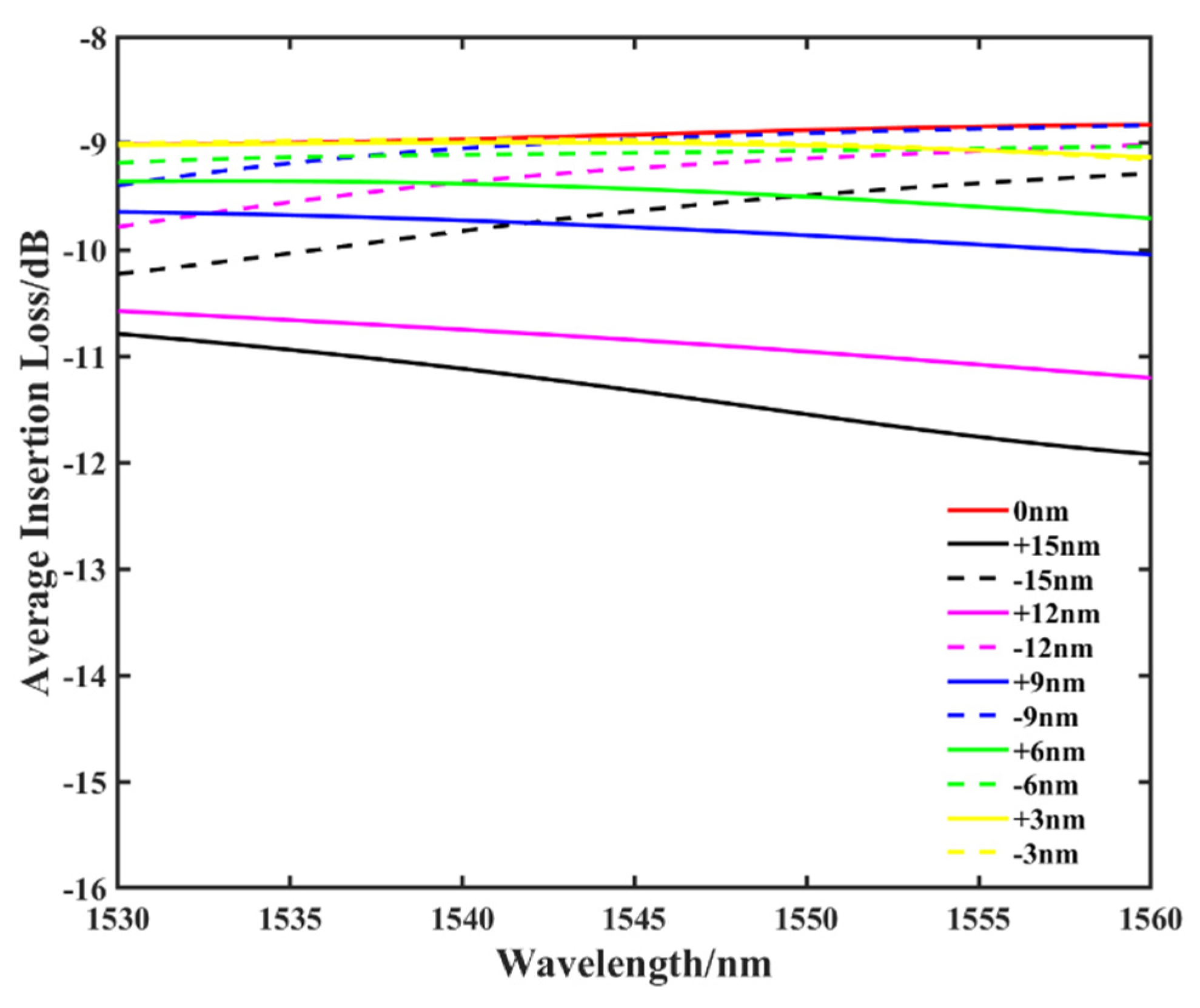
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gamet, J.; Pandraud, G. Ultralow-Loss 1 Times 8 Splitter Based on Field Matching Y Junction. IEEE Photonics Technol. Lett. 2004, 16, 2060–2062. [Google Scholar] [CrossRef]
- Tao, L.; Zakharian, A.R.; Fallahi, M.; Moloney, J.V.; Mansuripur, M. Multimode Interference-Based Photonic Crystal Waveguide Power Splitter. J. Lightwave Technol. 2004, 22, 2842–2846. [Google Scholar]
- Park, I.; Lee, H.S.; Kim, H.J.; Moon, K.M.; Lee, E.H. Photonic Crystal Power-Splitter Based on Directional Coupling. Opt. Express 2004, 12, 3599–3604. [Google Scholar] [CrossRef] [PubMed]
- Piggott, A.Y.; Petykiewicz, J.; Su, L.; Vu Kovi, J. Fabrication-Constrained Nanophotonic Inverse Design. Sci. Rep. 2017, 7, 1786. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Vučković, J. Nanophotonic computational design. Opt. Express 2013, 21, 13351–13367. [Google Scholar] [CrossRef] [PubMed]
- Molesky, S.; Lin, Z.; Piggott, A.Y.; Jin, W.; Vucković, J.; Rodriguez, A.W. Jelena Inverse Design in Nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Y.; Fan, S.; Miller, D. Demonstration of Systematic Photonic Crystal Device Design and Optimization by Low-Rank Adjustments: An Extremely Compact Mode Separator. Opt. Lett. 2005, 30, 141–143. [Google Scholar] [CrossRef]
- Piggott, A.Y.; Lu, J.; Lagoudakis, K.G.; Petykiewicz, J.; Babinec, T.M.; Vukovi, J. Inverse Design and Demonstration of a Compact and Broadband On-Chip Wavelength Demultiplexer. Nat. Photonics 2015, 9, 374–377. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.; Wang, P.; Polson, R.; Menon, R. Rajesh an Integrated-Nanophotonics Polarization Beamsplitter with 2.4 × 2.4 Mm2 Footprint. Nat. Photonics 2015, 9, 378–382. [Google Scholar] [CrossRef]
- Jensen, J.S.; Sigmund, O. Topology Optimization for Nano-Photonics. Laser Photonics Rev. 2011, 5, 308–321. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, K.; Wang, S.; Shen, W.; Xie, H.; Wang, Y.; Xiao, S.; Yao, Y.; Du, J.; He, Z.; et al. Arbitrarily Routed Mode-Division Multiplexed Photonic Circuits for Dense Integration. Nat. Commun. 2019, 10, 3263. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.; Polson, R.; Menon, R. Increasing the Density of Passive Photonic-Integrated Circuits Via Nanophotonic Cloaking. Nat. Commun. 2016, 7, 13126. [Google Scholar] [CrossRef]
- Yu, Z.; Cui, H.; Sun, X. Genetically Optimized On-Chip Wideband Ultracompact Reflectors and Fabry–Perot Cavities. Photonics Res. 2017, 5, B15–B19. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, X.; Xiao, Z.; Lu, C.; Zhang, X. Integrated Nanophotonic Wavelength Router Based on an Intelligent Algorithm. Optica 2019, 6, 1367. [Google Scholar] [CrossRef]
- Davis, A.J.; Hahlweg, C.F.; Mulley, J.R.; Callewaert, F.; Aydin, K. Inverse-designed all-dielectric waveguide bend. In Proceedings of the Novel Optical Systems Design & Optimization XIX, San Diego, CA, USA, 29–31 August 2016; p. 99480Q. [Google Scholar]
- Huang, J.; Yang, J.; Chen, D.; He, X.; Han, Y.; Zhang, J.; Zhang, Z. HAN Ultra-Compact Broadband Polarization Beam Splitter with Strong Expansibility. Photonics Res. 2018, 6, 574–578. [Google Scholar] [CrossRef]
- Nadell, C.C.; Huang, B.; Malof, J.M.; Padilla, W.J. Deep Learning for Accelerated All-Dielectric Metasurface Design. Opt. Express 2019, 27, 27523. [Google Scholar] [CrossRef]
- Liu, D.; Tan, Y.; Khoram, E.; Yu, Z. Training Deep Neural Networks for the Inverse Design of Nanophotonic Structures. ACS Photonics 2018, 5, 1365–1369. [Google Scholar] [CrossRef] [Green Version]
- Del Hougne, P.; Imani, M.F.; Diebold, A.V.; Horstmeyer, R.; Smith, D.R. Learned Integrated Sensing Pipeline: Reconfigurable Metasurface Transceivers as Trainable Physical Layer in an Artificial Neural Network. Adv. Sci. 2020, 7, 1901913. [Google Scholar] [CrossRef] [Green Version]
- Su, L.; Piggott, A.Y.; Sapra, N.V.; Petykiewicz, J.; Vu Kovi, J. Inverse Design and Demonstration of a Compact On-Chip Narrowband Three-Channel Wavelength Demultiplexer. ACS Photonics 2017, 5, 301–305. [Google Scholar] [CrossRef] [Green Version]
- Chang, W.; Xu, S.; Cheng, M.; Liu, D.; Zhang, M. Inverse Design of Single-Step-Etched Ultracompact Silicon Polarization Rotator. Opt. Express 2020, 28, 28343–28351. [Google Scholar] [CrossRef]
- Tahersima, M.H.; Kojima, K.; Koike-Akino, T.; Jha, D.; Wang, B.; Lin, C.; Parsons, K. Deep Neural Network Inverse Design of Integrated Photonic Power Splitters. Sci. Rep. 2019, 9, 1–9. [Google Scholar]
- Huang, J.; Ma, H.; Chen, D.; Yuan, H.; Zhang, J.; Li, Z.; Han, J.; Wu, J.; Yang, J. Digital Nanophotonics: The Highway to the Integration of Subwavelength-Scale Photonics: Ultra-Compact, Multi-Function Nanophotonic Design Based on Computational Inverse Design. Nanophotonics 2021, 10, 1011–1030. [Google Scholar] [CrossRef]
- Chhetri, B.B.; Yang, S.; Shimomura, T. Stochastic Approach in the Efficient Design of the Direct-Binary-Search Algorithm for Hologram Synthesis. Appl. Opt. 2000, 39, 5956–5964. [Google Scholar] [CrossRef]
- Ma, L.; Li, J.; Liu, Z.; Zhang, Y.; Zhang, N.; Zheng, S.; Lu, C. Intelligent Algorithms: New Avenues for Designing Nanophotonic Devices. Chin. Opt. Lett. 2021, 19, 011301. [Google Scholar] [CrossRef]
- Zhang, M.; Lu, L.; Zhou, F.; Liu, D. An Ultra-compact Colorless 50:50 Coupler Based on PhC-like Metamaterial Structure. In Proceedings of the 2016 Optical Fiber Communications Conference & Exhibition, Anaheim, CA, USA, 20–24 March 2016. [Google Scholar]
- Lu, L.; Liu, D.; Zhou, F.; Li, D.; Cheng, M.; Deng, L.; Fu, S.; Xia, J.; Zhang, M. Inverse-Designed Single-Step-Etched Colorless 3 dB Couplers Based On RIE-lag-insensitive PhC-like Subwavelength Structures. Opt. Lett. 2016, 41, 5051–5054. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Liu, Y.; Sun, W.; Wang, Y.; Ke, X.; Du, J.; He, Z.; Song, Q. Inversely Designed 1 × 4 Power Splitter with Arbitrary Ratios at 2-Mm Spectral Band. IEEE Photonics J. 2018, 10, 1–6. [Google Scholar] [CrossRef]
- Ke, X.; Lu, L.; Xiang, W.; Sun, W.; Song, Q. Integrated Photonic Power Divider with Arbitrary Power Ratios. Opt. Lett. 2017, 42, 855. [Google Scholar]
- Ma, H.; Huang, J.; Zhang, K.; Yang, J. Arbitrary-Direction, Multichannel and Ultra-Compact Power Splitters by Inverse Design Method. Opt. Commun. 2020, 462, 125329. [Google Scholar] [CrossRef]
- Abrokwah, K.O. Characterization and Modeling of Plasma Etch Pattern Dependencies in Integrated Circuits; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006; pp. 106–107. [Google Scholar]
- Ma, H.; Huang, J.; Zhang, K.; Yang, J. Inverse-Designed Arbitrary-Input and Ultra-Compact 1 × N Power Splitters Based on High Symmetric Structure. Sci. Rep. 2020, 10, 11757. [Google Scholar] [CrossRef]
- Shen, B.; Peng, W.; Polson, R.; Menon, R. Integrated Metamaterials for Efficient and Compact Free-Space-To-Waveguide Coupling. Opt. Express 2014, 22, 27175–27182. [Google Scholar] [CrossRef]
- Rashed, A.M.; Selviah, D.R. Modeling of a Polymer 1 × 3 MMI Power Splitter for Optical Backplane. In Proceedings of the Conference on Optoelectronic and Microelectronic Materials and Devices, Brisbane, QLD, Australia, 8–10 December 2004; pp. 281–284. [Google Scholar]
- Piggott, A.Y.; Ma, E.Y.; Su, L.; Ahn, G.H.; Sapra, N.V.; Vercruysse, D.; Netherton, A.M.; Khope, A.S.P.; Bowers, J.E.; Vučković, J. Inverse-Designed Photonics for Semiconductor Foundries. ACS Photonics 2020, 7, 569–575. [Google Scholar] [CrossRef]
- Meng, C.; Qiu, J.; Tian, Y.; Ye, Z.; Wu, J. A broadband compact 1 × 3 power splitter designed with inverse design method. In Proceedings of the 2016 15th International Conference on Optical Communications and Networks (ICOCN), Hangzhou, China, 24–27 September 2016. [Google Scholar]
- Lu, L.; Zhang, M.; Zhou, F.; Chang, W.; Tang, J.; Li, D.; Liu, D. Inverse-designed ultra-compact star-crossings based on PhC-like subwavelength structures for optical intercross connect. Opt. Express 2017, 25, 18355–18364. [Google Scholar] [CrossRef] [PubMed]
- Tao, S.H.; Fang, Q.; Song, J.F.; Yu, M.B.; Kwong, D.L. Cascade Wide-Angle Y-junction 1 × 16 Optical Power Splitter Based on Silicon Wire Waveguides on Silicon-On-Insulator. Opt. Express 2008, 16, 21456–21461. [Google Scholar] [CrossRef] [PubMed]
- Borel, P.I.; Frandsen, L.H.; Harp Th, A.; Kristensen, M.; Jensen, J.S.; Sigmund, O. Topology Optimised Broadband Photonic Crystal Y-splitter. Electron. Lett. 2005, 41, 69–71. [Google Scholar] [CrossRef]
- Wright, D.; Galarre Ta, C.; Sinev, I.; Alexeev, A.M.; Bertolotti, J. Selective Reconfigurable Multilevel Control of Resonant Modes in Hybrid All-Dielectric/Phase-Change Metasurfaces. Optica 2020, 7, 476–484. [Google Scholar]
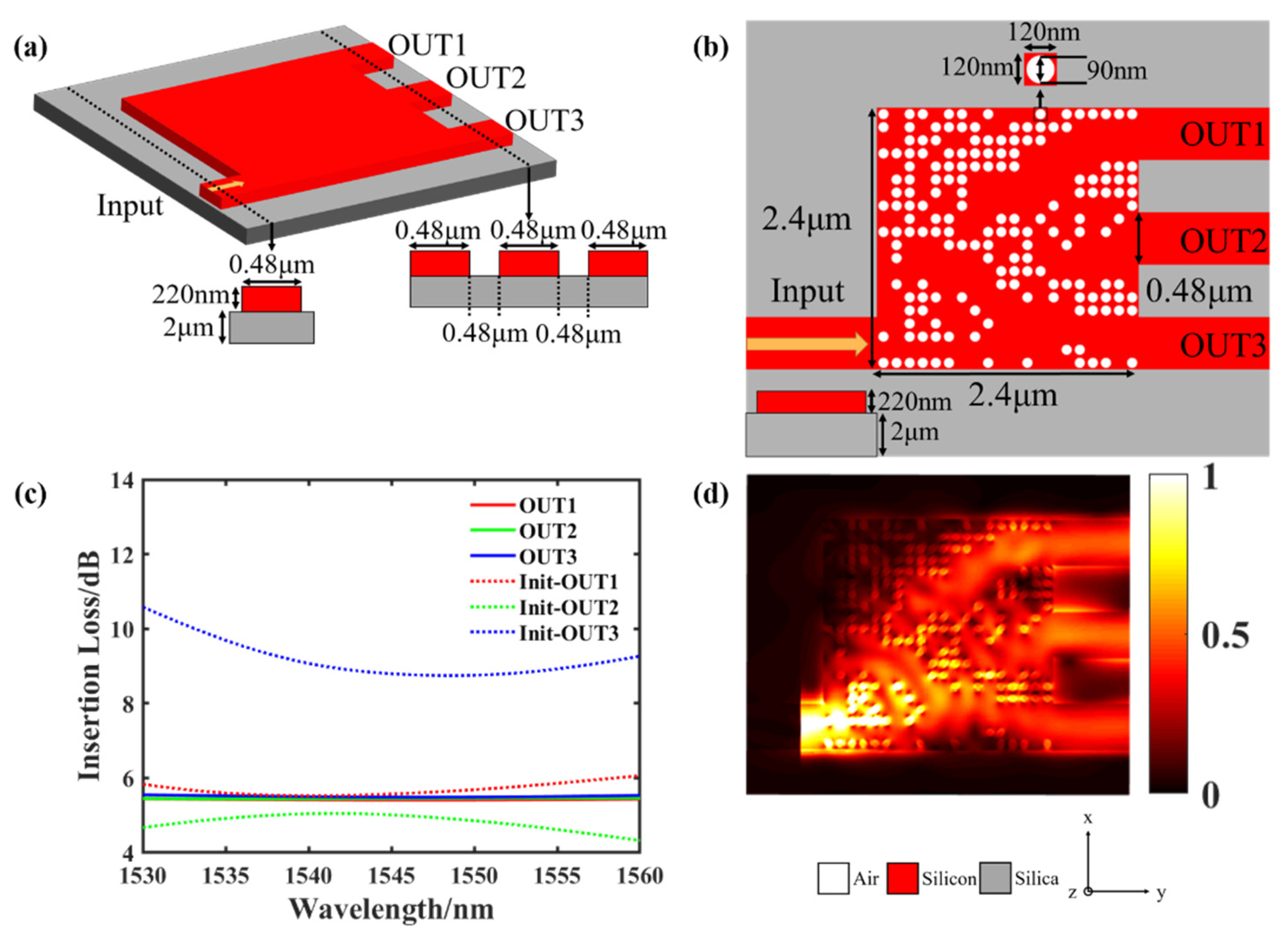

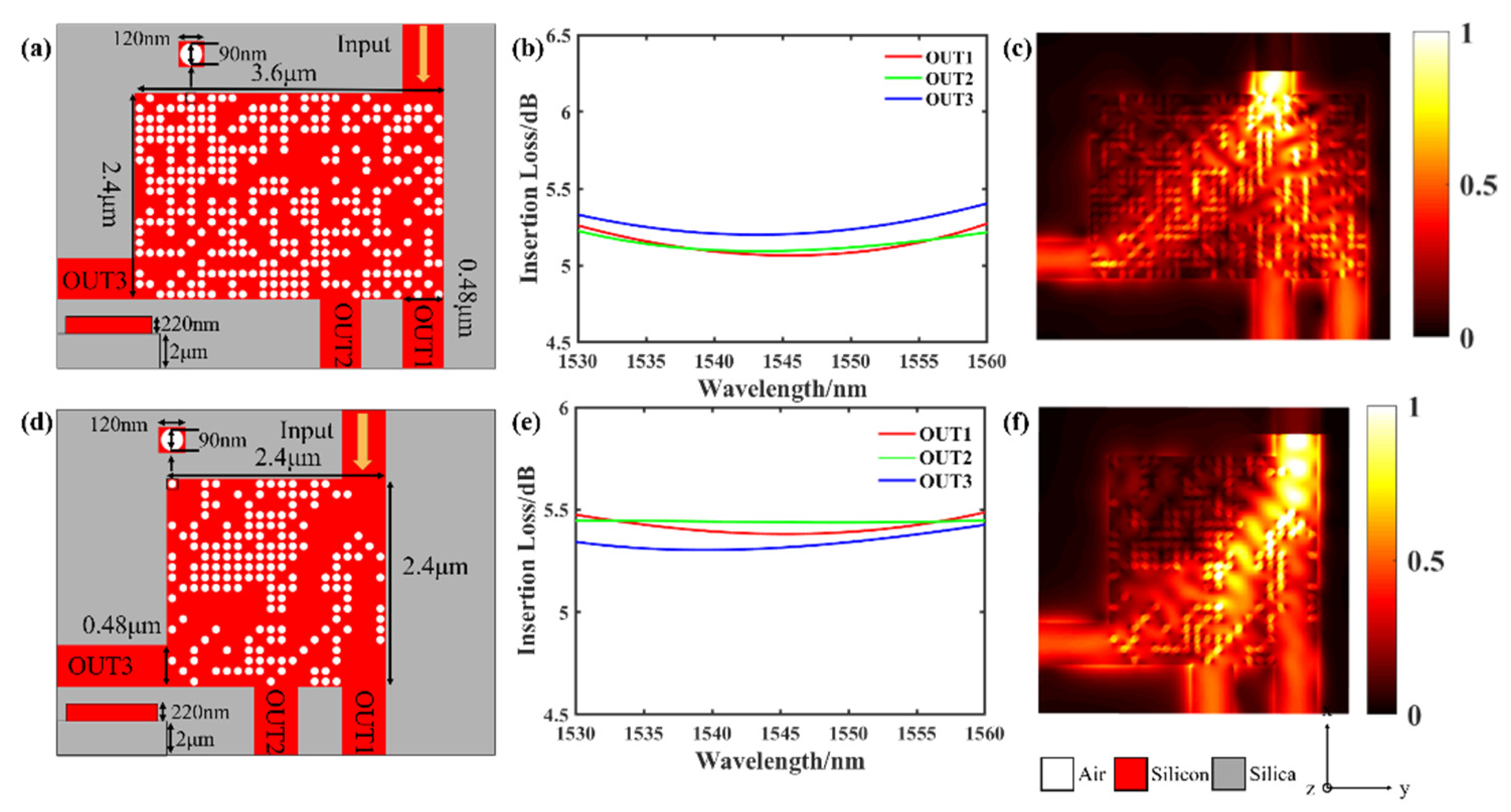


| References | Footprint | IL (EL [33]) | Direction (Directly Change the Propagation Direction after Power Splitting, without Adding Additional Waveguide Bending) | Cascading Combinations (after the Devices are Cascaded, the Performance Will Be Improved after Further Optimization) | Scalability (Combination to Realize 1 × N Power Splitter in Any Direction) |
|---|---|---|---|---|---|
| This Work | 2.4 × 2.4 μm | 5.55 dB (0.69 dB) | Directional flexibility | Yes | Yes |
| 5.49 dB (0.63 dB) | |||||
| 5.32 dB (0.48 dB) | |||||
| [34] | 23 × 292 μm | (0.4 dB) | Single direction | No | No |
| [4] | 3.8 × 2.5 μm | (0.642 dB) | Single direction | No | No |
| [35] | 3.8 × 2.5 μm | (0.4 dB) | Single direction | No | No |
| [36] | 2.8 × 2.8 μm | (0.49 dB) | Single direction | No | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Ma, H.; Xie, T.; Yang, J.; Zhang, Z. Ultra-Compact Power Splitters with Low Loss in Arbitrary Direction Based on Inverse Design Method. Photonics 2021, 8, 516. https://doi.org/10.3390/photonics8110516
Xu Y, Ma H, Xie T, Yang J, Zhang Z. Ultra-Compact Power Splitters with Low Loss in Arbitrary Direction Based on Inverse Design Method. Photonics. 2021; 8(11):516. https://doi.org/10.3390/photonics8110516
Chicago/Turabian StyleXu, Yanhong, Hansi Ma, Tong Xie, Junbo Yang, and Zhenrong Zhang. 2021. "Ultra-Compact Power Splitters with Low Loss in Arbitrary Direction Based on Inverse Design Method" Photonics 8, no. 11: 516. https://doi.org/10.3390/photonics8110516
APA StyleXu, Y., Ma, H., Xie, T., Yang, J., & Zhang, Z. (2021). Ultra-Compact Power Splitters with Low Loss in Arbitrary Direction Based on Inverse Design Method. Photonics, 8(11), 516. https://doi.org/10.3390/photonics8110516







