Spontaneous Emission Enhancement by a Rectangular-Aperture Optical Nanoantenna: An Intuitive Semi-Analytical Model of Surface Plasmon Polaritons
Abstract
:1. Introduction
2. Methods
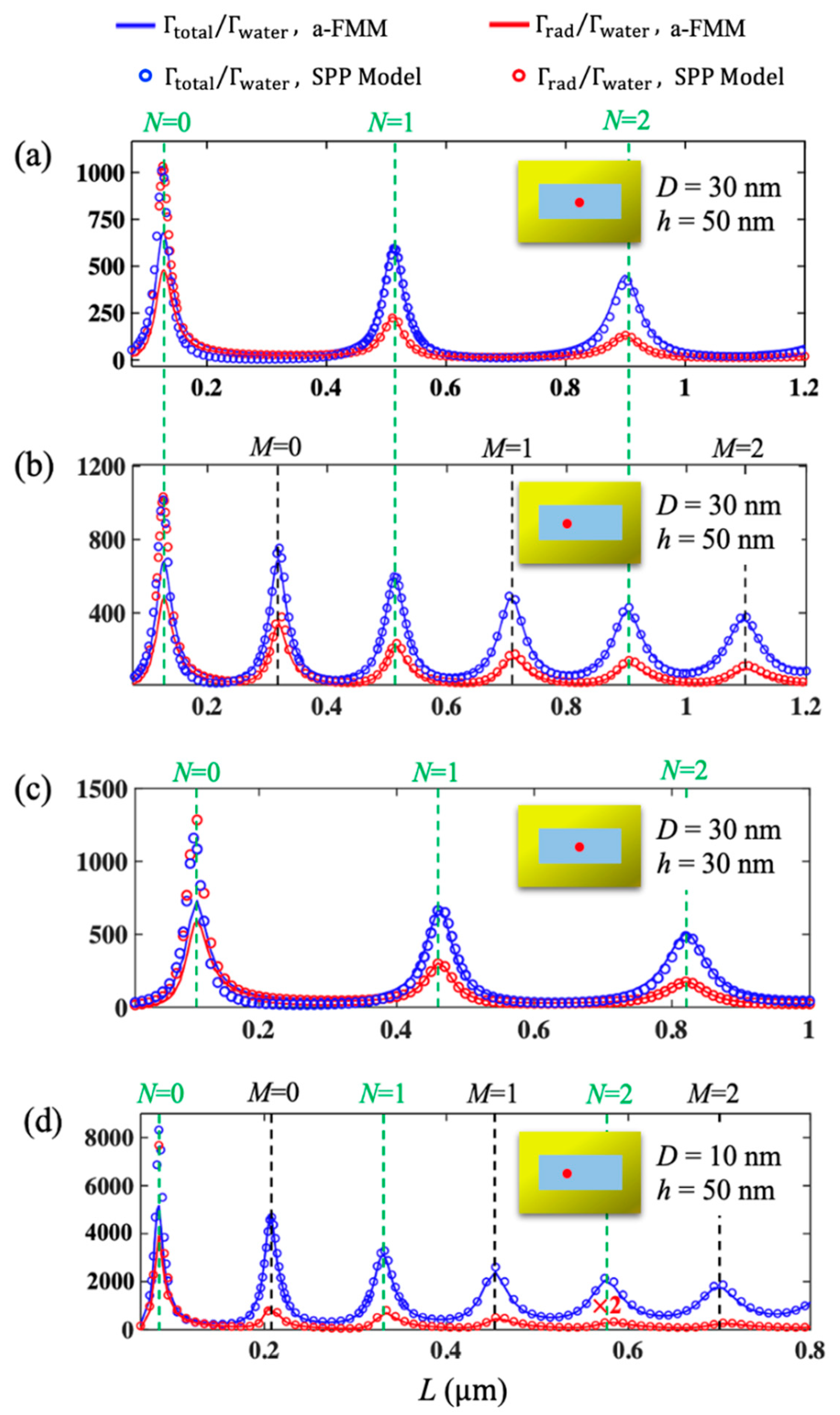
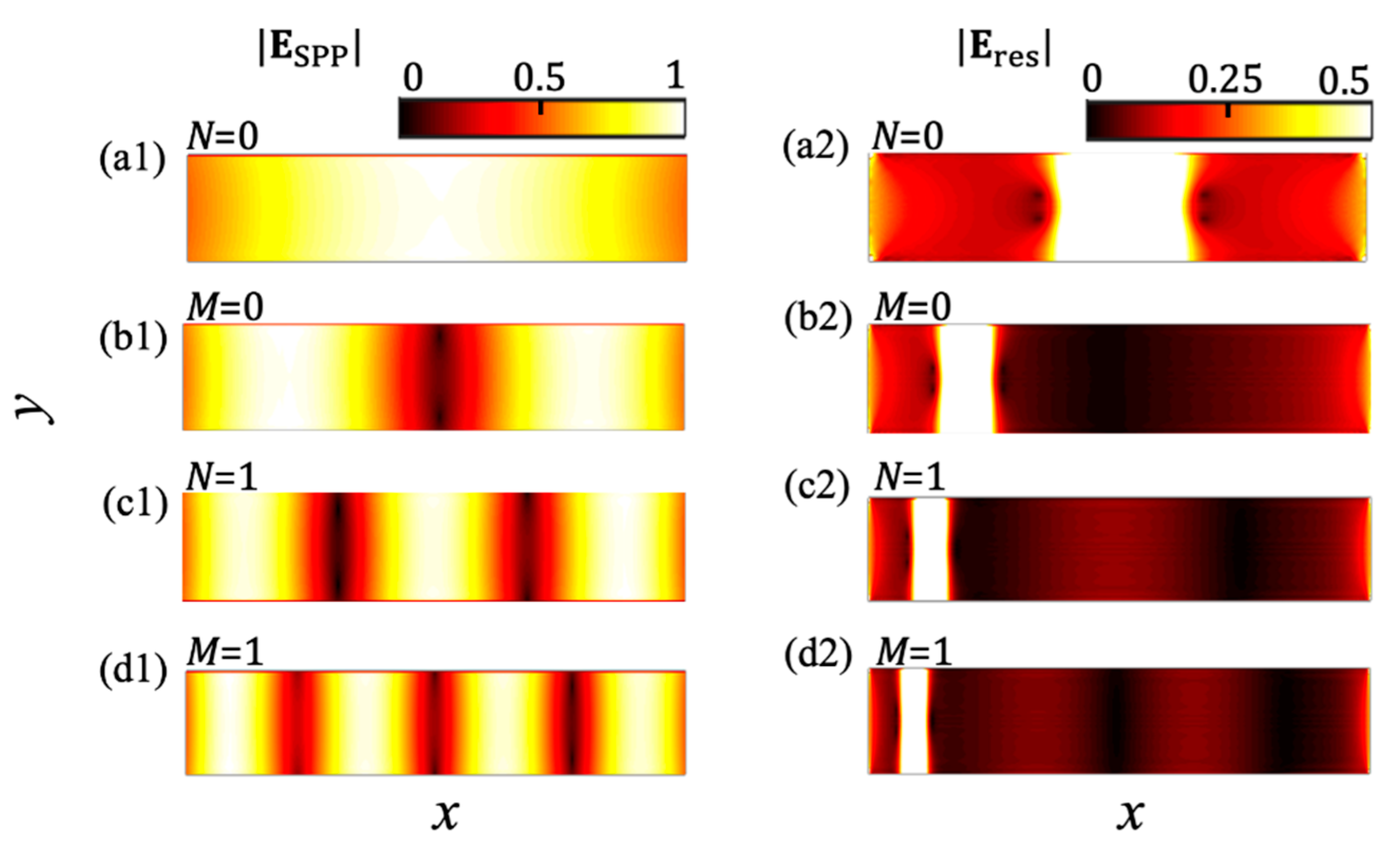
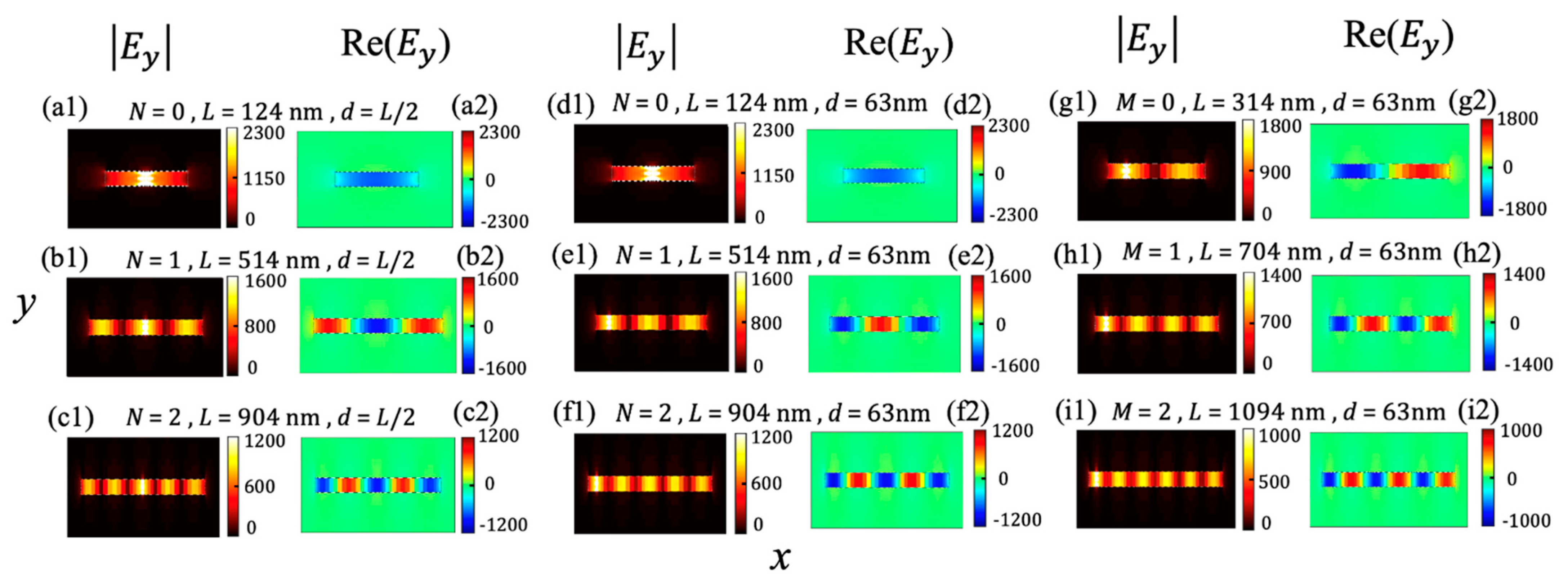
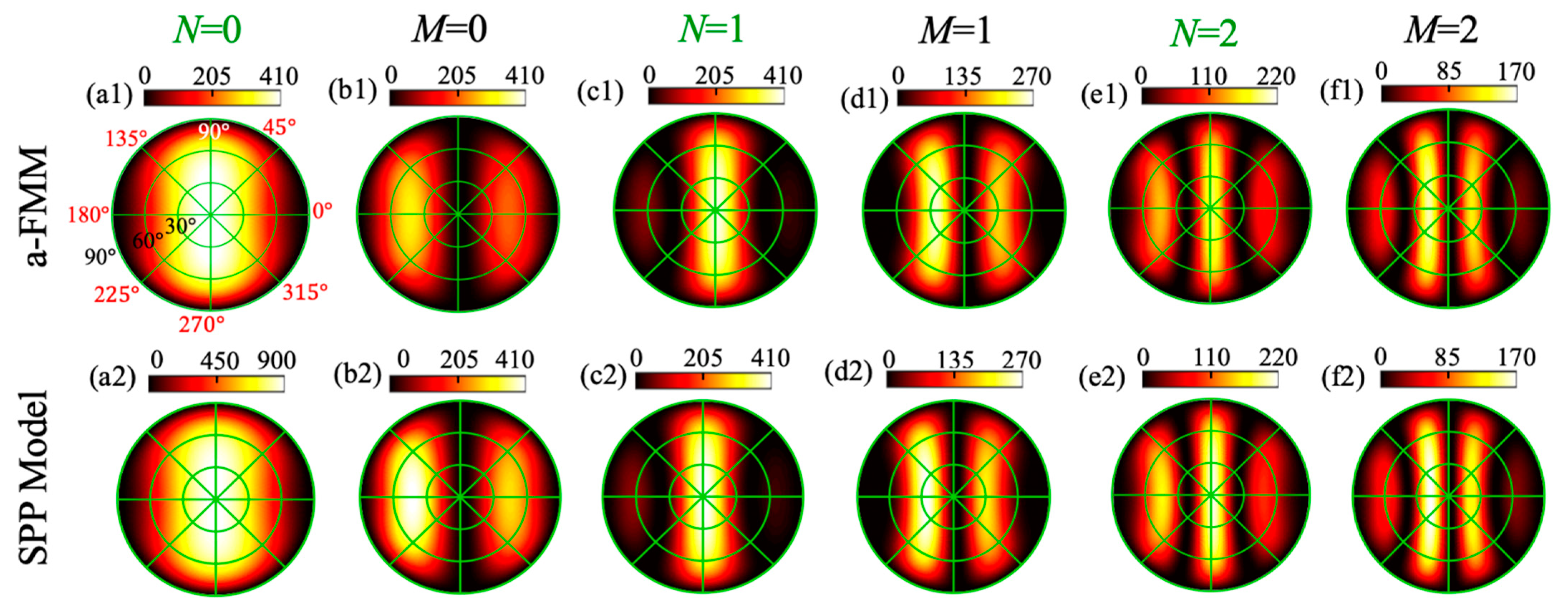
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ming, T.; Chen, H.; Jiang, R.; Li, Q.; Wang, J. Plasmon-controlled fluorescence: Beyond the intensity enhancement. J. Phys. Chem. Lett. 2012, 3, 191–202. [Google Scholar] [CrossRef]
- Agio, M. Optical antennas as nanoscale resonators. Nanoscale 2012, 4, 692–706. [Google Scholar] [CrossRef] [Green Version]
- Acuna, G.; Möller, F.; Holzmeister, P.; Beater, S.; Lalkens, B.; Tinnefeld, P. Fluorescence enhancement at docking sites of DNA-directed self-assembled nanoantennas. Science 2012, 338, 506–510. [Google Scholar] [CrossRef] [PubMed]
- Sergei, K.; Ulf, H.; Rogobete, L.; Sandoghdar, V. Enhancement of single-molecule fluorescence using a gold nanoparticle as an optical nanoantenna. Phys. Rev. Lett. 2006, 97, 017402. [Google Scholar]
- Punj, D.; Ghenuche, P.; Moparthi, S.B.; de Torres, J.; Grigoriev, V.; Rigneault, H.; Wenger, J. Plasmonic antennas and zero-mode waveguides to enhance single molecule fluorescence detection and fluorescence correlation spectroscopy toward physiological concentrations. Nat. Nanotechnol. 2014, 6, 268–282. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Liu, Y.; Yang, J.; Zhang, J. Single-molecule detection and radiation control in solutions at high concentrations via a heterogeneous optical slot antenna. Nanoscale 2014, 6, 9103–9109. [Google Scholar] [CrossRef]
- Genet, C.; Ebbesen, T.W. Light in tiny holes. Nature 2007, 445, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Levene, M.J.; Korlach, J.; Turner, S.W.; Foquet, M.; Craighead, H.G.; Webb, W.W. Zero-mode waveguides for single-molecule analysis at high concentrations. Science 2003, 299, 682–686. [Google Scholar] [CrossRef]
- Alam, M.S.; Karim, F.; Zhao, C. Single-molecule detection at high concentrations with optical aperture nanoantennas. Nanoscale 2016, 8, 9480–9487. [Google Scholar] [CrossRef]
- Fujimoto, K.; Morita, Y.; Iino, R.; Tomishige, M.; Shintaku, H.; Kotera, H.; Yokokawa, R. Simultaneous observation of kinesin-driven microtubule motility and binding of adenosine triphosphate using linear zero-mode waveguides. ACS Nano 2018, 12, 11975–11985. [Google Scholar] [CrossRef]
- Moran-Mirabal, J.M.; Craighead, H.G. Zero-mode waveguides: Sub-wavelength nanostructures for single molecule studies at high concentrations. Methods 2008, 46, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Pelton, M. Modified spontaneous emission in nanophotonic structures. Nat. Photonics 2015, 9, 427–435. [Google Scholar] [CrossRef]
- Miyake, T.; Tanii, T.; Sonobe, H.; Akahori, R.; Shimamoto, N.; Ueno, T.; Funatsu, T.; Ohdomari, I. Real-time imaging of single-molecule fluorescence with a zero-mode waveguide for the analysis of protein–protein interaction. Anal. Chem. 2008, 80, 6018–6022. [Google Scholar] [CrossRef]
- Wenger, J.; Lenne, P.-F.; Popov, E.; Rigneault, H.; Dintinger, J.; Ebbesen, T.W. Single molecule fluorescence in rectangular nano-apertures. Opt. Express 2005, 13, 7035–7044. [Google Scholar] [CrossRef]
- Zambrana-Puyalto, X.; Ponzellini, P.; Maccaferri, N.; Tessarolo, E.; Pelizzo, M.G.; Zhang, W.; Barbillon, G.; Lu, G.; Garoli, D. A hybrid metal–dielectric zero mode waveguide for enhanced single molecule detection. Chem. Commun. 2019, 55, 9725–9728. [Google Scholar] [CrossRef]
- Aouani, H.; Mahboub, O.; Devaux, E.; Rigneault, H.; Ebbesen, T.W.; Wenger, J. Large molecular fluorescence enhancement by a nanoaperture with plasmonic corrugations. Opt. Express 2011, 19, 13056–13062. [Google Scholar] [CrossRef] [PubMed]
- Park, Q.-H. Optical antennas and plasmonics. Contemp. Phys. 2009, 50, 407–423. [Google Scholar] [CrossRef] [Green Version]
- Seo, M.; Adam, A.; Kang, J.; Lee, J.; Ahn, K.; Park, Q.H.; Planken, P.; Kim, D. Near field imaging of terahertz focusing onto rectangular apertures. Opt. Express 2008, 16, 20484–20489. [Google Scholar] [CrossRef]
- El Eter, A.; Hameed, N.M.; Baida, F.I.; Salut, R.; Filiatre, C.; Nedeljkovic, D.; Atie, E.; Bole, S.; Grosjean, T. Fiber-integrated optical nano-tweezer based on a bowtie-aperture nano-antenna at the apex of a SNOM tip. Opt. Express 2014, 22, 10072–10080. [Google Scholar] [CrossRef] [PubMed]
- Jin, E.X.; Xu, X. Obtaining super resolution light spot using surface plasmon assisted sharp ridge nanoaperture. Appl. Phys. Lett. 2005, 86, 111106. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhang, W.; Zhu, X.; Yang, J.; Xu, J.; Yu, D. Resonant slot nanoantennas for surface plasmon radiation in optical frequency range. Appl. Phys. Lett. 2012, 100, 241115. [Google Scholar] [CrossRef]
- Yousif, B.B.; Samra, A.S. Modeling of optical nanoantennas. Phys. Res. Int. 2012, 2012, 321075. [Google Scholar] [CrossRef] [Green Version]
- Ponzellini, P.; Zambrana-Puyalto, X.; Maccaferri, N.; Lanzanò, L.; De Angelis, F.; Garoli, D. Plasmonic zero mode waveguide for highly confined and enhanced fluorescence emission. Nanoscale 2018, 10, 17362–17369. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Razinskas, G.; Vieker, H.; Gross, H.; Wu, X.; Beyer, A.; Gölzhäuser, A.; Hecht, B. High-Q, low-mode-volume and multiresonant plasmonic nanoslit cavities fabricated by helium ion milling. Nanoscale 2018, 10, 17148–17155. [Google Scholar] [CrossRef] [PubMed]
- Kotnala, A.; Ding, H.; Zheng, Y. Enhancing single-molecule fluorescence spectroscopy with simple and robust hybrid nanoapertures. ACS Photonics 2021, 8, 1673–1682. [Google Scholar] [CrossRef]
- Mahdavi, F.; Blair, S. Nanoaperture fluorescence enhancement in the ultraviolet. Plasmonics 2010, 5, 169–174. [Google Scholar] [CrossRef]
- Flauraud, V.; Regmi, R.; Winkler, P.M.; Alexander, D.T.; Rigneault, H.; Van Hulst, N.F.; García-Parajo, M.F.; Wenger, J.; Brugger, J. In-plane plasmonic antenna arrays with surface nanogaps for giant fluorescence enhancement. Nano Lett. 2017, 17, 1703–1710. [Google Scholar] [CrossRef] [Green Version]
- Ghenuche, P.; Mivelle, M.; de Torres, J.; Moparthi, S.B.; Rigneault, H.; Van Hulst, N.F.; García-Parajó, M.F.; Wenger, J. Matching nanoantenna field confinement to FRET distances enhances Forster energy transfer rates. Nano Lett. 2015, 15, 6193–6201. [Google Scholar] [CrossRef] [PubMed]
- Punj, D.; Mivelle, M.; Moparthi, S.B.; Van Zanten, T.S.; Rigneault, H.; Van Hulst, N.F.; Garcia-Parajo, M.F.; Wenger, J. A plasmonic ‘antenna-in-box’platform for enhanced single-molecule analysis at micromolar concentrations. Nat. Nanotechnol. 2013, 8, 512–516. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lalanne, P.; Yan, W.; Vynck, K.; Sauvan, C.; Hugonin, J.P. Light interaction with photonic and plasmonic resonances. Laser Photonics Rev. 2018, 12, 1700113. [Google Scholar] [CrossRef] [Green Version]
- Ching, E.; Leung, P.; van den Brink, A.M.; Suen, W.; Tong, S.; Young, K. Quasinormal-mode expansion for waves in open systems. Rev. Mod. Phys. 1998, 70, 1545–1554. [Google Scholar] [CrossRef] [Green Version]
- Teperik, T.; Popov, V.; García de Abajo, F.J. Giant light absorption by plasmons in a nanoporous metal film. Phys. Status Solidi A 2005, 202, 362–366. [Google Scholar] [CrossRef]
- Cetin, A.E.; Turkmen, M.; Aksu, S.; Etezadi, D.; Altug, H. Multi-resonant compact nanoaperture with accessible large nearfields. Appl. Phys. B Lasers Opt. 2015, 118, 29–38. [Google Scholar] [CrossRef]
- Wan, Y.; An, Y.; Tao, Z.; Deng, L. Manipulation of surface plasmon resonance of a graphene-based Au aperture antenna in visible and near-infrared regions. Opt. Commun. 2018, 410, 733–739. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic: San Diego, CA, USA, 1985. [Google Scholar]
- Jia, H.; Liu, H.; Zhong, Y. Role of surface plasmon polaritons and other waves in the radiation of resonant optical dipole antennas. Sci. Rep. 2015, 5, 8456. [Google Scholar] [CrossRef]
- Purcell, E.M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 1946, 69, 681. [Google Scholar]
- Bogdanov, S.I.; Shalaginov, M.Y.; Lagutchev, A.S.; Chiang, C.-C.; Shah, D.; Baburin, A.S.; Ryzhikov, I.A.; Rodionov, I.A.; Kildishev, A.V.; Boltasseva, A. Ultrabright room-temperature sub-nanosecond emission from single nitrogen-vacancy centers coupled to nanopatch antennas. Nano Lett. 2018, 18, 4837–4844. [Google Scholar] [CrossRef] [PubMed]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347–400. [Google Scholar] [CrossRef] [Green Version]
- Giannini, V.; Fernández-Domínguez, A.I.; Heck, S.C.; Maier, S.A. Plasmonic nanoantennas: Fundamentals and their use in controlling the radiative properties of nanoemitters. Chem. Rev. 2011, 111, 3888–3912. [Google Scholar] [CrossRef]
- Muskens, O.; Giannini, V.; Sánchez-Gil, J.A.; Gómez Rivas, J. Strong enhancement of the radiative decay rate of emitters by single plasmonic nanoantennas. Nano Lett. 2007, 7, 2871–2875. [Google Scholar] [CrossRef]
- Kinkhabwala, A.; Yu, Z.; Fan, S.; Avlasevich, Y.; Müllen, K.; Moerner, W.E. Large single-molecule fluorescence enhancements produced by a bowtie nanoantenna. Nat. Photonics 2009, 3, 654–657. [Google Scholar] [CrossRef]
- Ma, R.M.; Oulton, R.F.; Sorger, V.J.; Zhang, X. Plasmon lasers: Coherent light source at molecular scales. Laser Photonics Rev. 2013, 7, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Tsakmakidis, K.L.; Boyd, R.W.; Yablonovitch, E.; Zhang, X. Large spontaneous-emission enhancements in metallic nanostructures: Towards LEDs faster than lasers. Opt. Express 2016, 24, 17916–17927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hugonin, J.P.; Lalanne, P. Perfectly matched layers as nonlinear coordinate transforms: A generalized formalization. J. Opt. Soc. Am. A 2005, 22, 1844–1849. [Google Scholar] [CrossRef]
- Liu, H. DIF CODE for Modeling Light Diffraction in Nanostructures; Nankai University: Tianjin, China, 2010. [Google Scholar]
- Zhu, J.; Zhu, T.; Jia, H.; Zhong, Y.; Liu, H. Intuitive analysis of subwavelength plasmonic trench waveguide. J. Lightwave Technol. 2019, 37, 1345–1351. [Google Scholar] [CrossRef]
- Vassallo, C. Optical Waveguide Concepts; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Jia, H.; Lalanne, P.; Liu, H. Comprehensive surface-wave description for the nano-scale energy concentration with resonant dipole antennas. Plasmonics 2016, 11, 1025–1033. [Google Scholar] [CrossRef]
- Sauvan, C.; Hugonin, J.-P.; Maksymov, I.S.; Lalanne, P. Theory of the spontaneous optical emission of nanosize photonic and plasmon resonators. Phys. Rev. Lett. 2013, 110, 237401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Hugonin, J.-P.; Lalanne, P. Near-to-far field transformations for radiative and guided waves. ACS Photonics 2016, 3, 395–402. [Google Scholar] [CrossRef] [Green Version]
- Taminiau, T.H.; Stefani, F.D.; van Hulst, N.F. Optical nanorod antennas modeled as cavities for dipolar emitters: Evolution of sub-and super-radiant modes. Nano Lett. 2011, 11, 1020–1024. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhai, X.; Wang, N.; Zhong, Y.; Liu, H. Broadband enhancement of the spontaneous emission by a split-ring nanoantenna: Impact of azimuthally propagating surface plasmon polaritons. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 4600815. [Google Scholar] [CrossRef]
- Bauch, M.; Toma, K.; Toma, M.; Zhang, Q.; Dostalek, J. Plasmon-enhanced fluorescence biosensors: A review. Plasmonics 2014, 9, 781–799. [Google Scholar] [CrossRef] [Green Version]
- Aouani, H.; Mahboub, O.; Bonod, N.; Devaux, E.; Popov, E.; Rigneault, H.; Ebbesen, T.W.; Wenger, J. Bright unidirectional fluorescence emission of molecules in a nanoaperture with plasmonic corrugations. Nano Lett. 2011, 11, 637–644. [Google Scholar] [CrossRef]
- Aouani, H.; Mahboub, O.; Devaux, E.; Rigneault, H.; Ebbesen, T.W.; Wenger, J. Plasmonic antennas for directional sorting of fluorescence emission. Nano Lett. 2011, 11, 2400–2406. [Google Scholar] [CrossRef]
- Chang, Y.-T.; Lai, Y.-C.; Li, C.-T.; Chen, C.-K.; Yen, T.-J. A multi-functional plasmonic biosensor. Opt. Express 2010, 18, 9561–9569. [Google Scholar] [CrossRef]
- Tobing, L.Y.; Goh, G.-Y.; Mueller, A.D.; Ke, L.; Luo, Y.; Zhang, D.-H. Polarization invariant plasmonic nanostructures for sensing applications. Sci. Rep. 2017, 7, 7539. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Liu, H.; Zhong, Y. Impact of surface plasmon polaritons and other waves on the radiation of a dipole emitter close to a metallic nanowire antenna. Opt. Express 2014, 22, 25539–25549. [Google Scholar] [CrossRef] [PubMed]
- Hasan, S.B.; Filter, R.; Ahmed, A.; Vogelgesang, R.; Gordon, R.; Rockstuhl, C.; Lederer, F. Relating localized nanoparticle resonances to an associated antenna problem. Phys. Rev. B 2011, 84, 195405. [Google Scholar] [CrossRef] [Green Version]
- Friedler, I.; Sauvan, C.; Hugonin, J.P.; Lalanne, P.; Claudon, J.; Gérard, J.M. Solid-state single photon sources: The nanowire antenna. Opt. Express 2009, 17, 2095–2110. [Google Scholar] [CrossRef]
- Liu, H.; Lalanne, P. Light scattering by metallic surfaces with subwavelength patterns. Phys. Rev. B 2010, 82, 115418. [Google Scholar] [CrossRef]
- Zhang, L.; Fu, Q.; Tan, Y.; Li, X.; Deng, Y.; Zhou, Z.-K.; Zhou, B.; Xia, H.; Chen, H.; Qiu, C.-W. Metaoptronic multiplexed interface for probing bioentity behaviors. Nano Lett. 2021, 21, 2681–2689. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; You, J.-B.; Liu, J.; Xiong, X.; Li, Z.; Png, C.E.; Wu, L.; Qiu, C.-W.; Zhou, Z.-K. Steering room-temperature plexcitonic strong coupling: A diexcitonic perspective. Nano Lett. 2021, 21, 8979–8986. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhai, X.; Tao, C.; Wang, N.; Zhong, Y.; Liu, H. Spontaneous Emission Enhancement by a Rectangular-Aperture Optical Nanoantenna: An Intuitive Semi-Analytical Model of Surface Plasmon Polaritons. Photonics 2021, 8, 572. https://doi.org/10.3390/photonics8120572
Zhang X, Zhai X, Tao C, Wang N, Zhong Y, Liu H. Spontaneous Emission Enhancement by a Rectangular-Aperture Optical Nanoantenna: An Intuitive Semi-Analytical Model of Surface Plasmon Polaritons. Photonics. 2021; 8(12):572. https://doi.org/10.3390/photonics8120572
Chicago/Turabian StyleZhang, Xinyue, Xuelin Zhai, Can Tao, Ning Wang, Ying Zhong, and Haitao Liu. 2021. "Spontaneous Emission Enhancement by a Rectangular-Aperture Optical Nanoantenna: An Intuitive Semi-Analytical Model of Surface Plasmon Polaritons" Photonics 8, no. 12: 572. https://doi.org/10.3390/photonics8120572
APA StyleZhang, X., Zhai, X., Tao, C., Wang, N., Zhong, Y., & Liu, H. (2021). Spontaneous Emission Enhancement by a Rectangular-Aperture Optical Nanoantenna: An Intuitive Semi-Analytical Model of Surface Plasmon Polaritons. Photonics, 8(12), 572. https://doi.org/10.3390/photonics8120572




