Optical Phenomena in Mesoscale Dielectric Particles
Abstract
1. Introduction
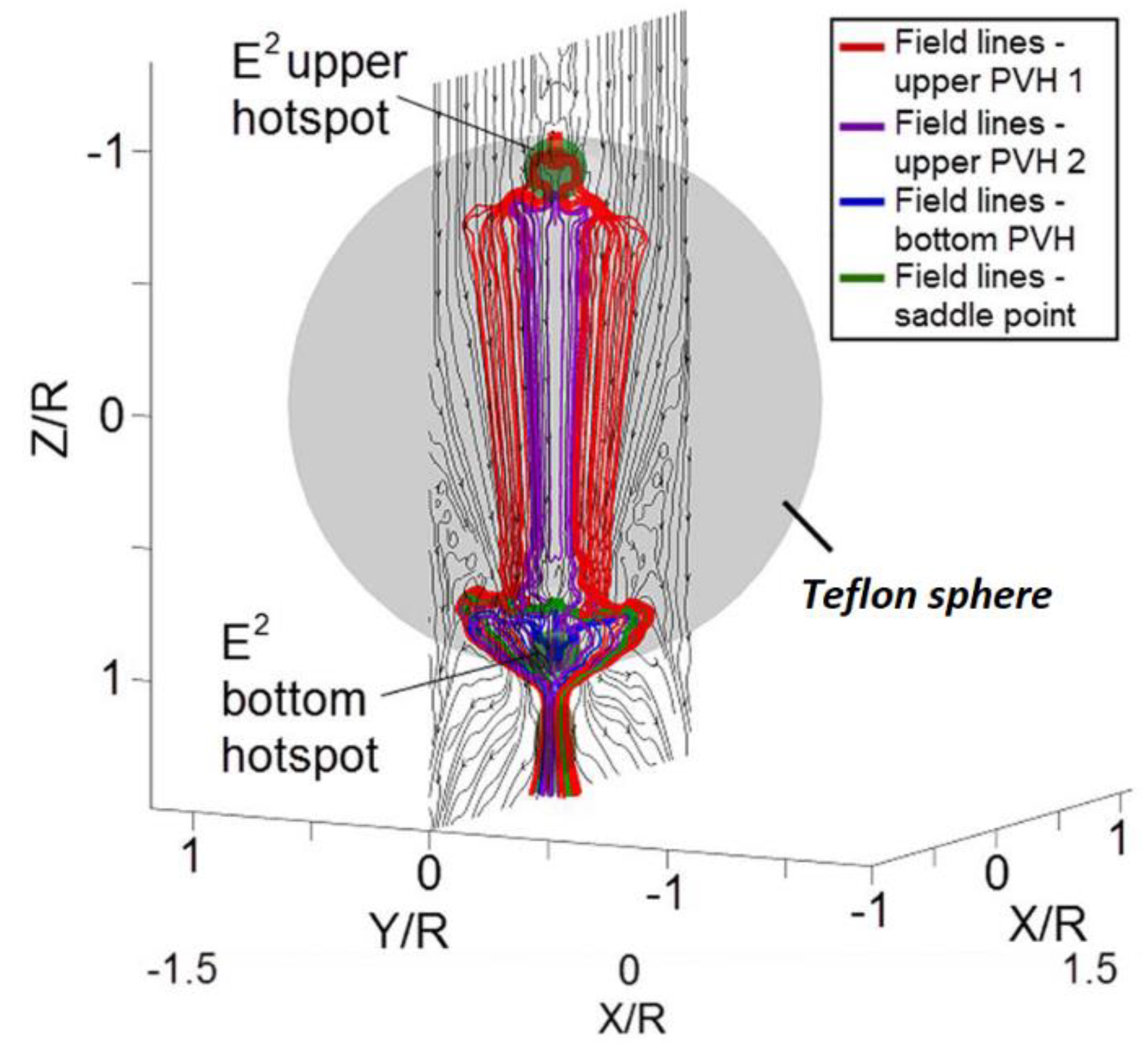
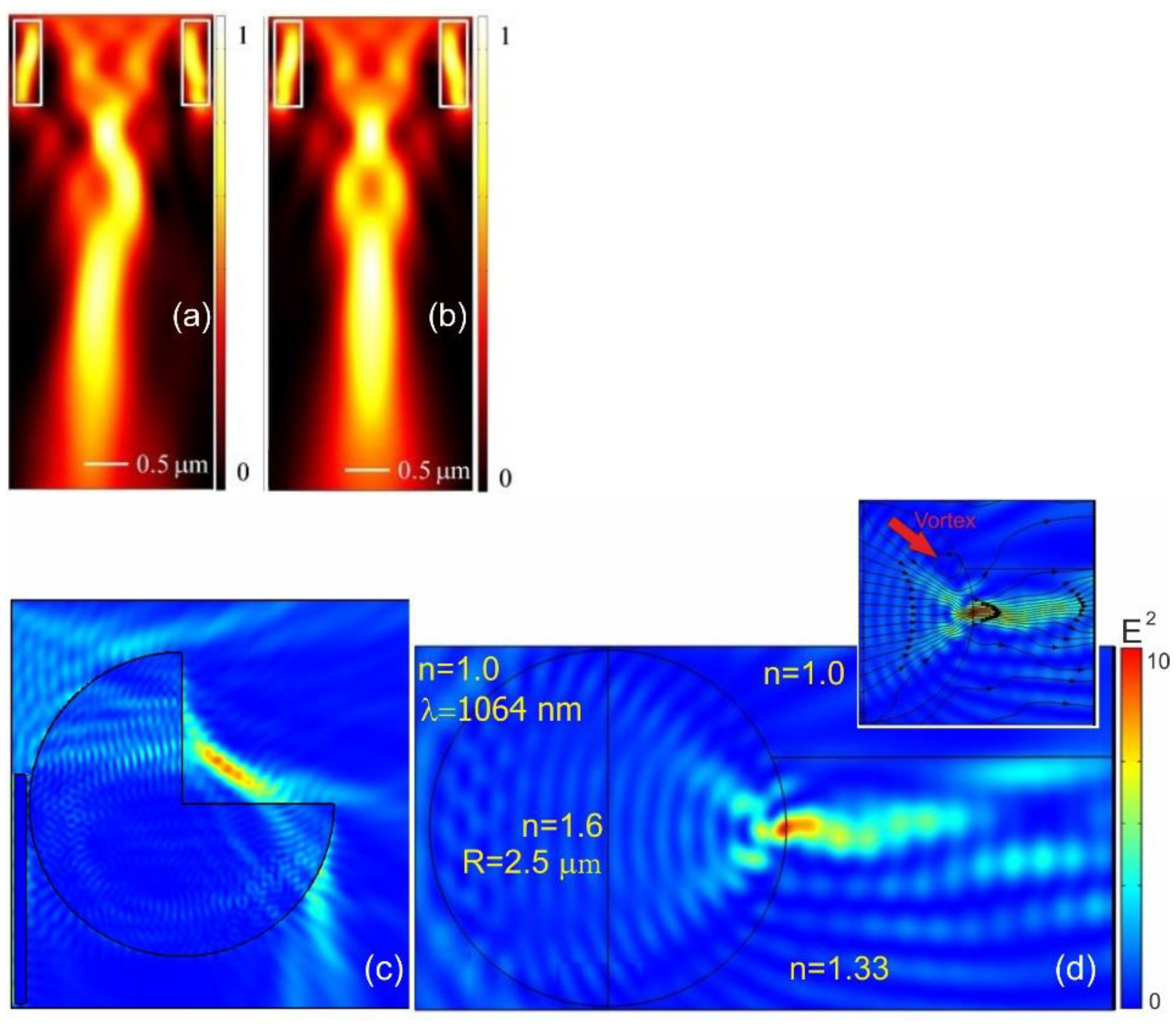
2. Optical Optical Whirlpools, Nano-Vortices, Optical Hearts
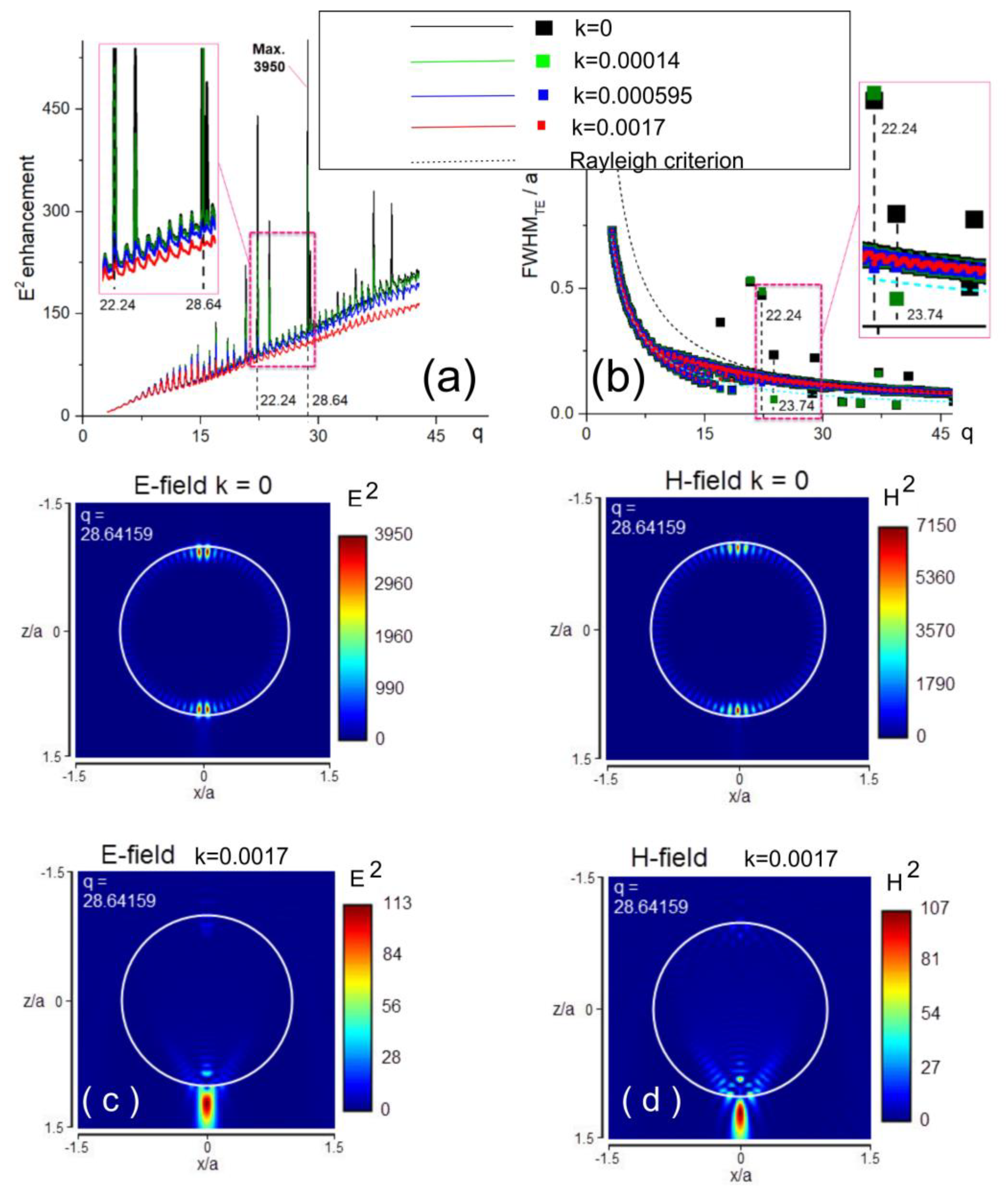
3. Fano Resonances in Dielectric Mie Resonance Mesophotonics
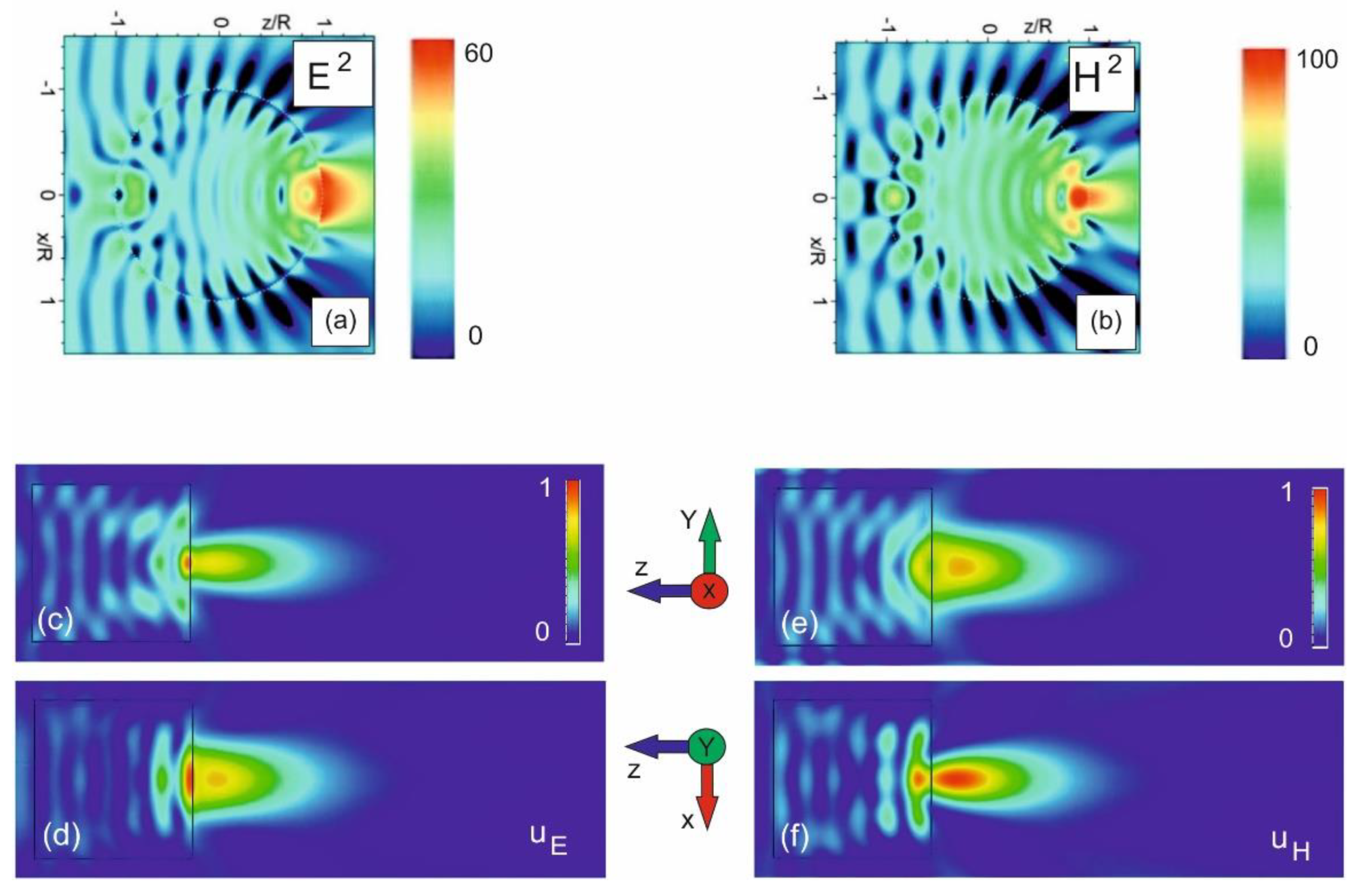
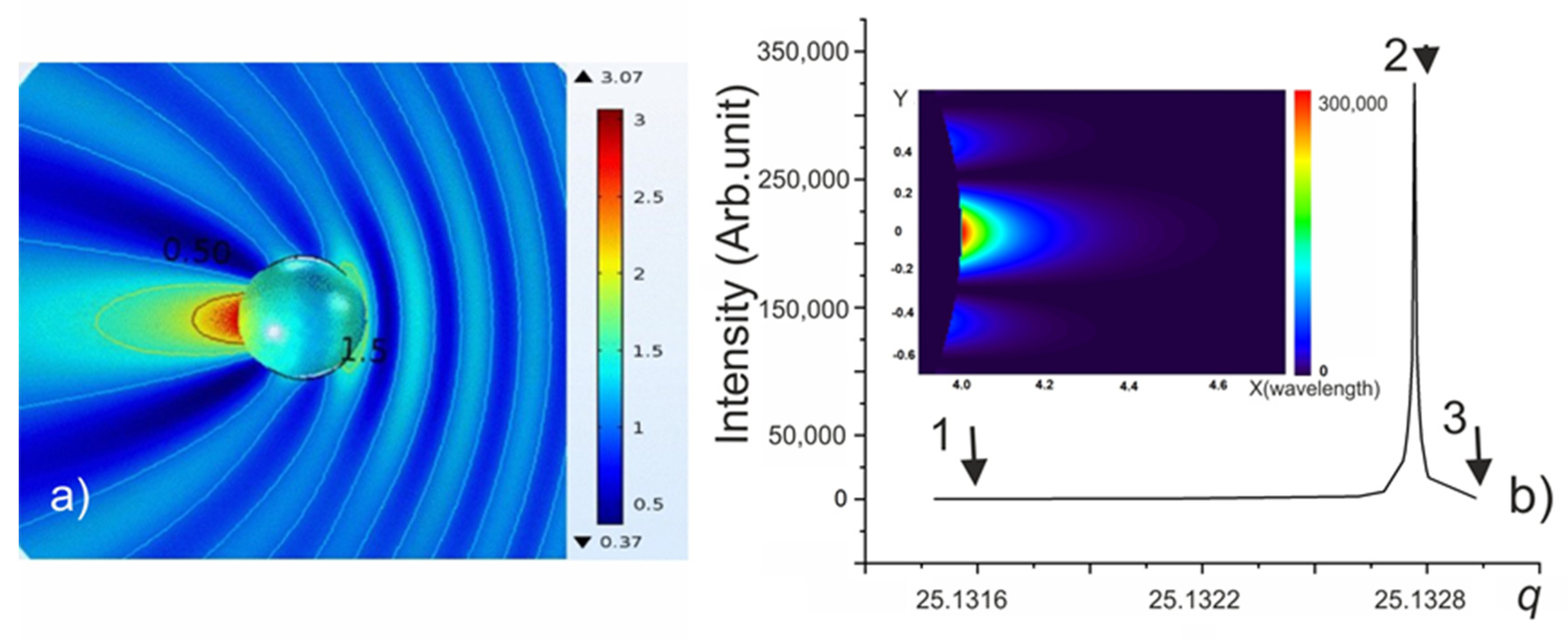
4. Giant Magnetic Field Generation in Mesoscale Particles
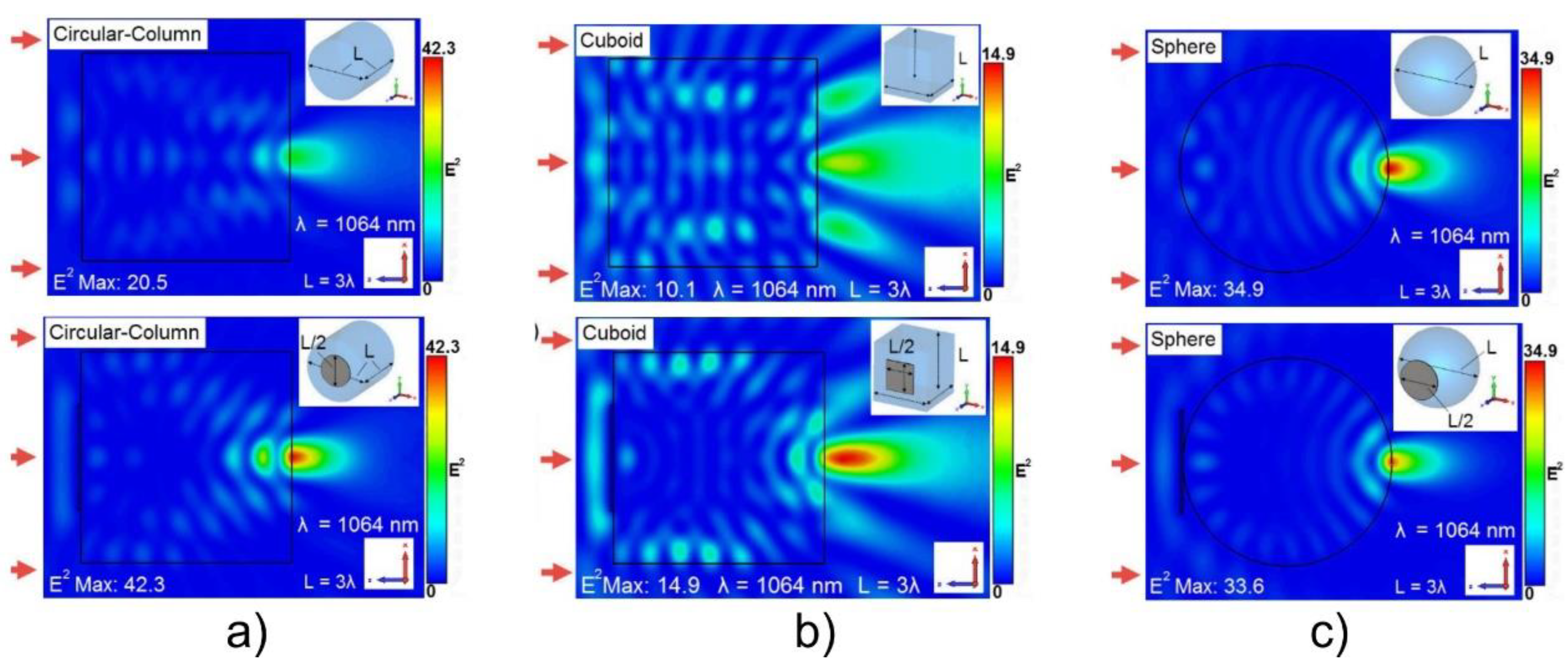
5. Photonic Nanojets
Photonic Jet: Electric or Magnetic?
6. Anomalous Apodization Effect
7. Tangential Electric Field Component Control
8. Terajets
9. Anomalous Gouy Phase Shift
10. Waveguide Systems Based on Dielectric Particles Chain
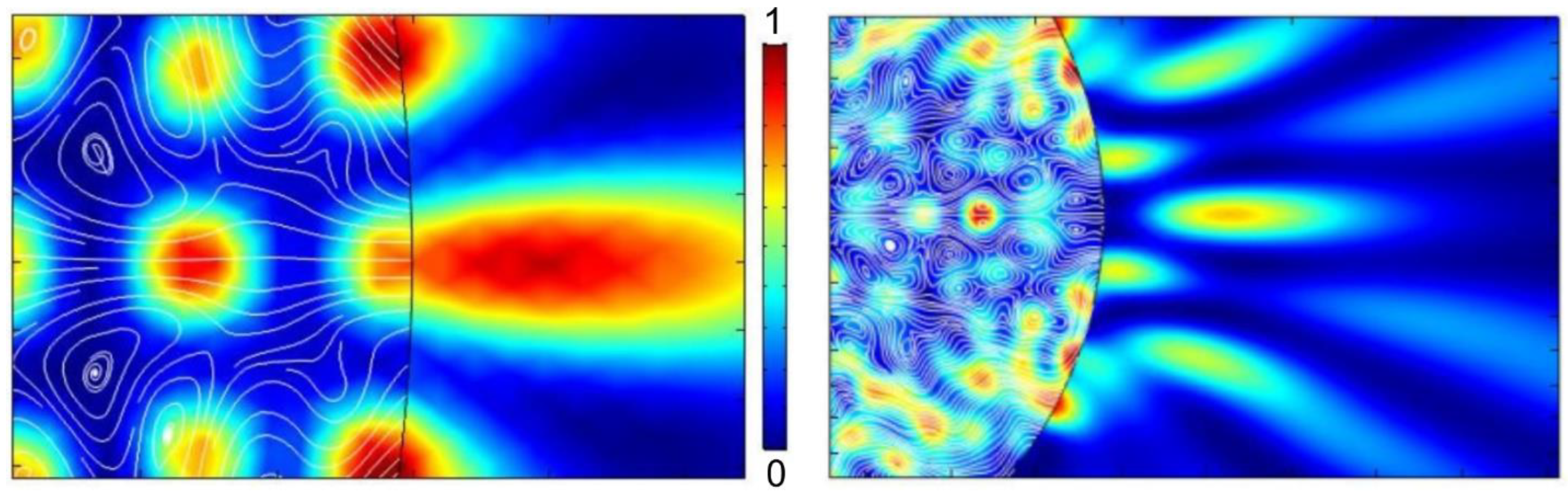
11. Specular-Reflection Photonic Nanojet
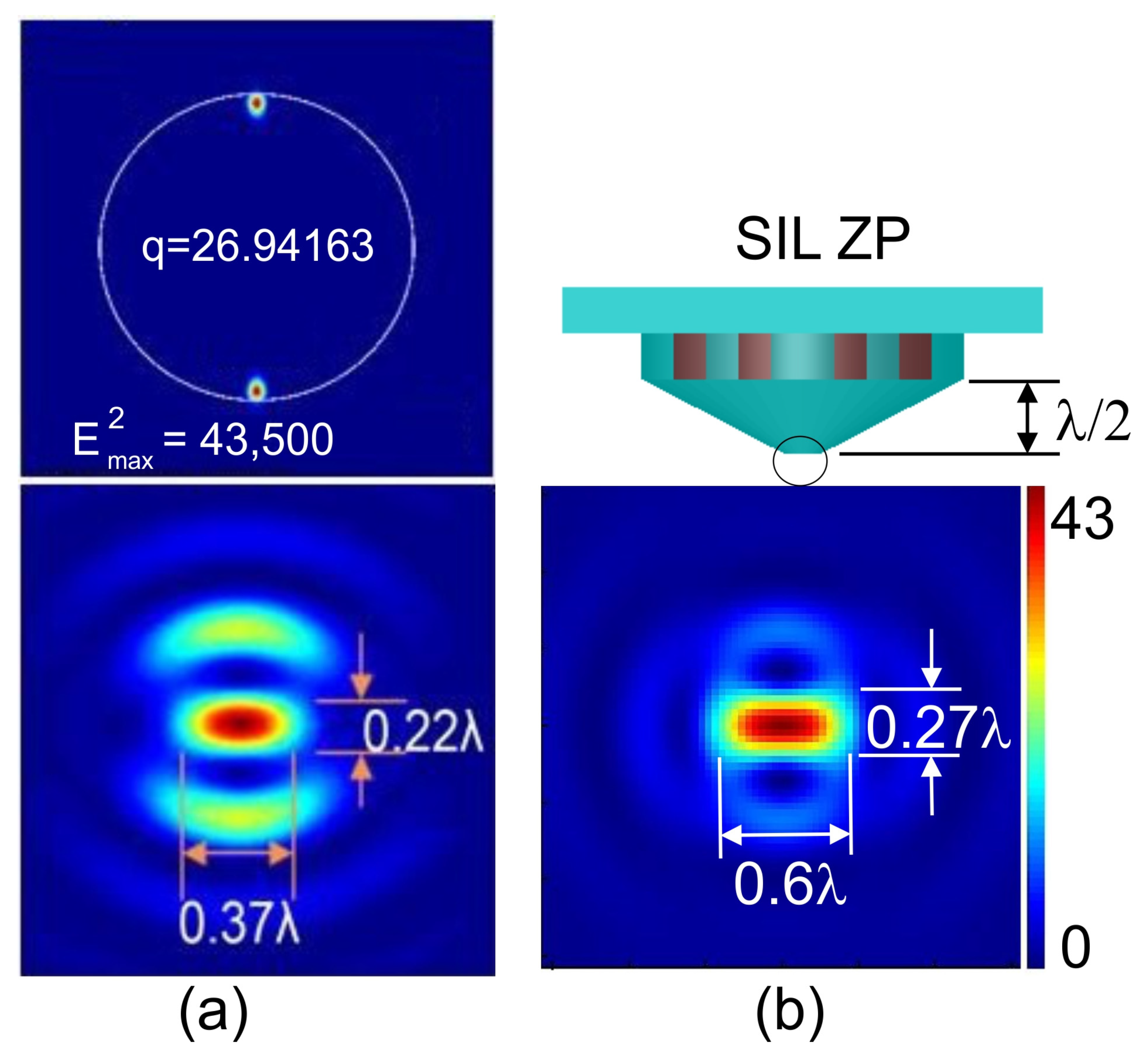
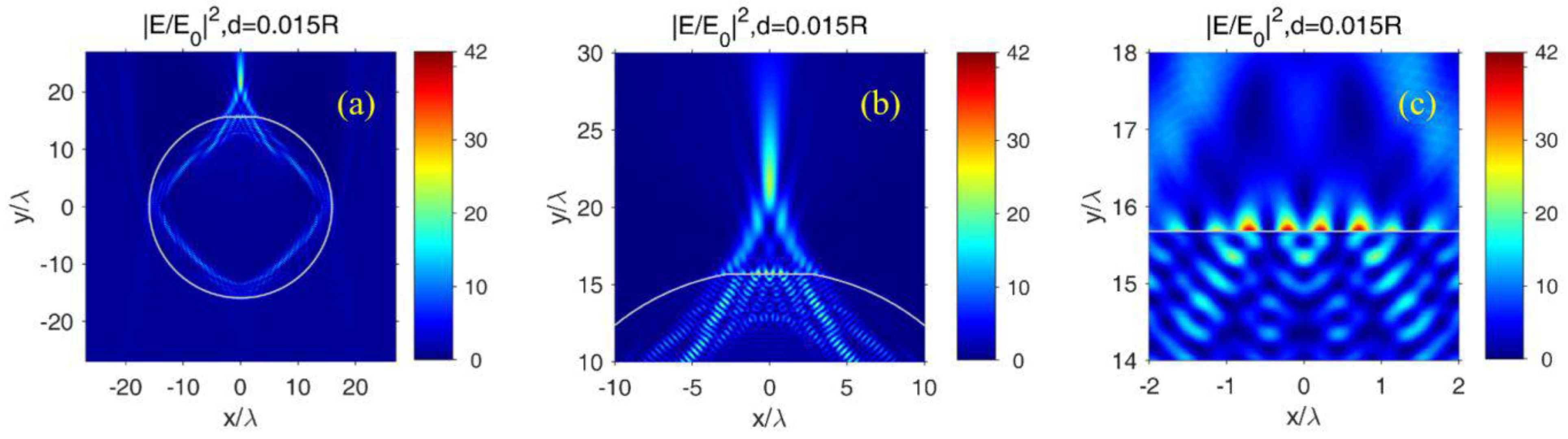
12. Overcoming the Diffraction Limit and Image Quality Improvement
13. Nanostructured Particles with Refractive Index near 2
14. Structured Fields in the Form of Photonic Hooks and Loops
15. Low-Dimensional Systems. Plasmonic Jets and Hooks
16. Acoustic Jets and Hooks
17. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mie, G. Contributions to the optics of turbid media, particularly of colloidal metal solutions. Ann. Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Ternovsky, V. Light scattering by a thin wire with a surface-plasmon resonance: Bifurcations of the Poynting vector field. Phys. Rev. B 2006, 73, 235432. [Google Scholar] [CrossRef]
- Bashevoy, M.; Fedotov, V.; Zheludev, N. Optical whirlpool on an absorbing metallic nanoparticle. Opt. Express 2005, 13, 8372. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Miroshnichenko, A.; Kivshar, Y. Fano resonances and topological optics: An interplay of far- and near-field interference phenomena. J. Opt. 2013, 15, 73001. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Paniagua-Domınguez, R.; Minin, I.V.; Minin, O.V.; Wang, Z. Refractive index less than two: Photonic nanojets yesterday, today and tomorrow. Opt. Mater. Express 2017, 7, 1820–1847. [Google Scholar] [CrossRef]
- Yue, L.; Yan, B.; Monks, J.; Dhama, R.; Jiang, C.; Minin, O.V.; Minin, I.V.; Wang, Z. Full three-dimensional Poynting vector flow analysis of great field-intensity enhancement in specifically sized spherical-particles. Sci. Rep. 2019, 9, 20224. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Luk’yanchuk, B.; Yue, L.; Yan, B.; Monks, J.; Dhama, R.; Minin, O.V.; Minin, I.V.; Huang, S.; Fedyanin, A. High order Fano resonances and giant magnetic fields in dielectric microspheres. Sci. Rep. 2019, 9, 20293. [Google Scholar] [CrossRef]
- Yue, L.; Wang, Z.; Yan, B.; Monks, J.; Joya, Y.; Dhama, R.; Minin, O.V.; Minin, I.V. Super-Enhancement Focusing of Teflon Spheres. Ann. Phys. 2020, 532, 2000373. [Google Scholar] [CrossRef]
- Berry, M.V. Superoscillations and leaky spectra. J. Phys. A Math. Theor. 2018, 52, 15202. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Yuan, G.H. Optical superoscillation technologies beyond the diffraction limit. Nat. Rev. Phys. 2021. [Google Scholar] [CrossRef]
- Sakharov, A.D. Magnetoimplosive generators. Sov. Phys. Uspekhi. 1966, 9, 294–299. [Google Scholar] [CrossRef]
- Minin, V.F.; Minin, I.V.; Minin, O.V. Calculation Experiment Technology. In Computational Fluid Dynamics; InTechOpen: London, UK, 2011. [Google Scholar] [CrossRef]
- Chen, Z.; Taflove, A.; Backman, V. Photonic nanojet enhancement of backscattering of light by nanoparticles: A potential novel visible-light ultramicroscopy technique. Opt. Express 2004, 12, 1214–1220. [Google Scholar] [CrossRef]
- Benincasa, D.S.; Barber, P.W.; Zhang, J.-Z.; Hsieh, W.-F.; Chang, R.K. Spatial distribution of the internal and near-field intensities of large cylindrical and spherical scatterers. Appl. Opt. 1987, 26, 1348–1356. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Zheng, Y.; Lu, Y. Laser cleaning of solid surface: Optical resonance and near-field effects. Proc. SPIE 2000, 4065, 576–587. [Google Scholar]
- Lu, Y.; Zhang, L.; Song, W.; Zheng, Y.; Luk’yanchuk, B. Laser writing of a subwavelength structure on silicon (100) surfaces with particle-enhanced optical irradiation. JETP Lett. 2000, 72, 457–459. [Google Scholar] [CrossRef]
- Mosbacher, M.; Münzer, H.; Zimmermann, J.; Solis, J.; Boneberg, J.; Leiderer, P. Optical field enhancement effects in laser-assisted particle removal. Appl. Phys. A 2001, 72, 41–44. [Google Scholar]
- Wang, J.; Gouesbet, G.; Gréhan, G.; Han, Y.; Saengkaew, S. Morphology-dependent resonances in an eccentrically layered sphere illuminated by a tightly focused off-axis Gaussian beam: Parallel and perpendicular beam incidence. J. Opt. Soc. Am. A 2011, 28, 1849. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Taflove, A.; Backman, V. Optical analysis of nanoparticles via enhanced backscattering facilitated by 3-D photonic nanojets. Opt. Express 2005, 13, 526. [Google Scholar] [CrossRef]
- Yousefi, M.; Scharf, T.; Rossi, M. Photonic nanojet generation under converging and diverging beams. J. Opt. Soc. Am. B 2021, 38, 317–326. [Google Scholar] [CrossRef]
- Wang, H.; Hao, J.; Zhang, B.; Han, C.; Zhao, C.; Shen, Z.; Xu, J.; Ding, J. Donut-like photonic nanojet with reverse energy flow. Chin. Opt. Lett. 2021, 19, 102602. [Google Scholar] [CrossRef]
- Lecler, C.; Takakura, Y.; Meyrueis, P. Properties of a three-dimensional photonic jet. Opt. Lett. 2005, 30, 2641–2643. [Google Scholar] [CrossRef] [PubMed]
- Minin, I.V.; Minin, O.V.; Gagnon, N.; Petosa, A. FDTD Analysis of a Flat Diffractive Optics with Sub-Reyleigh Limit Resolution in MM/THz Waveband. In Proceedings of the 2006 Joint 31st International Conference on Infrared Millimeter Waves and 14th International Conference on Teraherz Electronics, Shanghai, China, 18–22 September 2006; p. 170. [Google Scholar]
- Minin, I.V.; Minin, O.V. Experimental verification 3D subwavelength resolution beyond the diffraction limit with zone plate in millimeter wave. Microw. Opt. Technol. Lett. 2014, 56, 2436–2439. [Google Scholar] [CrossRef]
- Liu, C.; Kaiser, T.; Lange, S.; Schweiger, G. Structural resonances in a dielectric sphere illuminated by an evanescent wave. Opt. Commun. 1995, 117, 521–531. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Diffractive Optics and Nanophotonics: Resolution Below the Diffraction Limit; Springer: Berlin, Germany, 2016. [Google Scholar]
- Minin, I.V.; Minin, O.V. Photonics of isolated dielectric particles of arbitrary 3D shape—A new direction of optical information technologies. Vestnik NSU 2014, 12, 59–70. [Google Scholar]
- Minin, I.V.; Minin, O.V.; Geints, Y. Localized EM and photonic jets from non-spherical and non-symmetrical dielectric mesoscale objects: Brief review. Ann. Phys. 2015, 527, 491–502. [Google Scholar] [CrossRef]
- Cui, X.; Erni, D.; Hafner, C. Optical forces on metallic nanoparticles induced by a photonic nanojet. Opt. Express 2008, 16, 13560. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xin, H.; Liu, X.; Zhang, Y.; Lei, H.; Li, B. Trapping and Detection of Nanoparticles and Cells Using a Parallel Photonic Nanojet Array. ACS Nano 2016, 10, 5800. [Google Scholar] [CrossRef] [PubMed]
- Shakhov, A.; Astafiev, A.; Nadtochenko, V. Microparticle manipulation using femtosecond photonic nanojet-assisted laser cavitation. Opt. Lett. 2018, 43, 1858. [Google Scholar] [CrossRef]
- Surdo, S.; Duocastella, M.; Diaspro, A. Nanopatterning with Photonic Nanojets: Review and Perspectives in Biomedical Research. Micromachines 2021, 12, 256. [Google Scholar] [CrossRef]
- Lu, D.; Pedroni, M.; Labrador-Paez, L.; Marques, M.; Jaque, D.; Haro-Gonzalez, P. Nanojet Trapping of a Single Sub-10 nm Upconverting Nanoparticle in the Full Liquid Water Temperature Range. Nano Micro Small 2021, 17, 2006764. [Google Scholar] [CrossRef] [PubMed]
- Killian, J.; Ye, F.; Wang, M. Optical Tweezers: A Force to Be Reckoned With. Cell 2018, 175, 1445–1448. [Google Scholar] [CrossRef]
- Shan, X.; Wang, F.; Wang, D.; Wen, S.; Chen, C.; Di, X.; Nie, P.; Liao, J.; Liu, Y.; Ding, L.; et al. Optical tweezers beyond refractive index mismatch using highly doped upconversion nanoparticles. Nat. Nanotechnol. 2021, 16, 531–537. [Google Scholar] [CrossRef]
- Zhang, W.; Lei, H. Fluorescence enhancement based on cooperative effects of a photonic nanojet and plasmon resonance. Nanoscale 2020, 12, 6596–6602. [Google Scholar] [CrossRef]
- Bratchenko, L.; Bratchenko, I.; Khristoforova, Y.; Artemyev, D.; Konovalova, D.; Lebedev, P.; Zakharov, V. Raman spectroscopy of human skin for kidney failure detection. J. Biophotonics 2020, 14, e202000360. [Google Scholar] [CrossRef]
- Hüser, L.; Lehmann, P. Microsphere-assisted interference microscopy for resolution enhancement. tm Tech. Mess. 2021, 88, 311–318. [Google Scholar] [CrossRef]
- Li, P.; Li, G.; Yu, H.; Wang, F.; Liu, L.; Li, W. Advances in Dielectric Microspherical Lens Nanoscopy: Label-Free Superresolution Imaging. IEEE Nanotechnol. Mag. 2021, 15, 38. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Miroshnichenko, A.; Fu, Y.; Zhang, J.; Luk’yanchuk, B. Magnetic light. Sci. Rep. 2012, 2, 492. [Google Scholar] [CrossRef] [PubMed]
- Albella, P.; Poyli, M.; Schmidt, M.; Maier, S.; Moreno, F.; Saénz, J.; Aizpurua, J. Low-Loss Electric and Magnetic Field-Enhanced Spectroscopy with Subwavelength Silicon Dimers. J. Phys. Chem. C 2013, 117, 13573–13584. [Google Scholar] [CrossRef]
- Bakker, R.; Permyakov, D.; Yu, Y.; Markovich, D.; Paniagua-Domínguez, R.; Gonzaga, L.; Samusev, A.; Kivshar, Y.; Luk’yanchuk, B.; Kuznetsov, A. Magnetic and electric hotspots with silicon nanodimers. Nano Lett. 2015, 15, 2137–2142. [Google Scholar] [CrossRef]
- Li, C.; Kattawar, G.; Zhai, P. Electric and magnetic energy density distributions inside and outside dielectric particles illuminated by a plane electromagnetic wave. Opt. Express 2005, 13, 4554. [Google Scholar] [CrossRef]
- Baranov, D.; Savelev, R.; Li, S.; Krasnok, A.; Alu, A. Modifying magnetic dipole spontaneous emission with nanophotonic structures. Laser Photonics Rev. 2017, 11, 1600268. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Yan, B.; Yue, L.; Wang, Z. Engineering near-field focusing of a microsphere lens with pupil masks. Opt. Commun. 2016, 370, 140. [Google Scholar] [CrossRef]
- Wu, M.; Chen, R.; Soh, J.; Shen, Y.; Jiao, L.; Wu, J.; Chen, X.; Ji, R.; Hong, M. Super-focusing of center-covered engineered microsphere. Sci. Rep. 2016, 6, 31637. [Google Scholar] [CrossRef] [PubMed]
- Minin, I.V.; Minin, O.V. Patent of Russia 21, N 153686, 2015.
- Yue, L.; Yan, B.; Monks, J.; Dhama, R.; Wang, Z.; Minin, O.V.; Minin, I.V. V. Intensity-Enhanced Apodization Effect on an Axially Illuminated Circular-Column Particle-Lens. Ann. Phys. 2017, 530, 1700384. [Google Scholar] [CrossRef]
- Yue, L.; Yan, B.; Monks, J.; Wang, Z.; Tung, N.; Lam, V.; Minin, O.V.; Minin, I.V. Production of photonic nanojets by using pupil-masked 3D dielectric cuboid. J. Phys. D Appl. Phys. 2017, 50, 175102. [Google Scholar] [CrossRef]
- Yue, L.; Yan, B.; Monks, J.; Wang, Z.; Tung, N.; Lam, V.; Minin, O.V.; Minin, I.V. A millimetre-wave cuboid solid immersion lens with intensity-enhanced amplitude mask apodization. J. Infrared Milli Terahz Waves 2018, 39, 546–552. [Google Scholar] [CrossRef]
- Liu, C.; Chen, W.; Geints, Y.; Minin, O.V.; Minin, I.V. Simulation and experimental observations of axial position control of photonic nanojet by dielectric cube with metal screen. Opt. Lett. 2021, 46, 4292–4295. [Google Scholar] [CrossRef]
- Liu, C.; Chen, W.; Minin, O.V.; Minin, I.V. Multispectral photonic jet shaping and steering by control of tangential electric field component on cuboid particle. Photonics 2021, 8, 317. [Google Scholar] [CrossRef]
- Dorofeev, I.; Suslyaev, V.; Minin, O.V.; Minin, I.V. Role of the tangential electric field component to the terahertz jet and hook formation by dielectric cube and sphere. Opt. Eng. 2021, 60, 82004. [Google Scholar] [CrossRef]
- Ling, J.; Li, D.; Liu, X.; Wang, X. Ultra-long focusing of microsphere lens via wavefront reconstruction in microsphere. Proc. SPIE 2018, 10964, 109642D. [Google Scholar]
- Pacheco-Pena, V.; Beruete, M.; Minin, I.V.; Minin, O.V. Terajets produced by 3D dielectric cuboids. Appl. Phys. Lett. 2014, 105, 84102. [Google Scholar]
- Zhao, L.; Ong, C.K. Direct observation of photonic jets and corresponding backscattering enhancement at microwave frequencies. J. Appl. Phys. 2009, 105, 123512. [Google Scholar] [CrossRef]
- Pacheco-Pena, V.; Beruete, M.; Minin, I.V.; Minin, O.V. Multifrequency focusing and wide angular scanning of Terajets. Optic Lett. 2015, 40, 245. [Google Scholar] [CrossRef]
- Khodzitsky, M.; Vozianova, A.; Gill, V.; Chernyadiev, A.; Grebenchukov, A.; Minin, I.V.; Minin, O.V. Formation of terahertz beams produced by artificial dielectric periodical structures. Proc. SPIE 2016, 9918, 99182X. [Google Scholar]
- Minin, I.V.; Minin, O.V.; Delgado-Notario, J.A.; Calvo-Gallego, J.; Velázquez-Pérez, J.E.; Ferrando-Bataller, M.; Meziani, Y.M. Improvement of a terahertz detector performance using the terajet effect in a mesoscale dielectric cube: Proof of concept. Phys. Status Solidi-Rapid Res. Lett. 2020, 14, 1900700. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Salvador-Sanchez, J.; Delgado-Notario, J.A.; Calvo-Gallego, J.; Ferrando-Bataller, M.; Fobelets, K.; Velázquez-Pérez, J.E.; Meziani, Y.M. Responsivity enhancement of a strained silicon field effect transistor detector at 0.3 THz using the terajet effect. Opt. Lett. 2021, 46, 3061–3064. [Google Scholar] [CrossRef] [PubMed]
- Minin, O.V.; Minin, I.V.; Meziani, Y.M.; Hisatake, S. Improvement of a point-contact detector performance using the terajet effect initiated by photonics. Opt. Eng. 2020, 60, 82005. [Google Scholar] [CrossRef]
- Dorofeev, I.; Dunaevsky, G.; Suslyaev, V.; Minin, I.V.; Minin, O.V. Small-sized body influence on the quality factor increasing of quasioptical resonator. Opt. Quantum Electron. 2017, 49, 355. [Google Scholar] [CrossRef]
- Samura, Y.; Horio, K.; Antipov, V.B.; Shipilov, S.E.; Eremeev, A.I.; Minin, O.V.; Minin, I.V.; Hisatake, S. Characterization of mesoscopic dielectric cuboid antenna at millimeter-wave band. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1828–1832. [Google Scholar] [CrossRef]
- Yamada, K.; Samura, Y.; Minin, O.V.; Kanno, A.; Sekine, N.; Nakajima, J.; Minin, I.V.; Hisatake, S. Short-range Wireless Transmission in the 300-GHz Band Using Low-profile Wavelength-scaled Dielectric Cuboid Antennas. Front. Comms. Net. 2021, 2, 702968. [Google Scholar] [CrossRef]
- Wang, D.; Chen, X.; Fang, X.; Tang, J.; Lin, F.; Wang, X.; Liu, G.; Liao, L.; Ho, J.C.; Wei, Z. Photoresponse improvement of mixed-dimensional 1D–2D GaAs photodetectors by incorporating constructive interface states. Nanoscale 2021, 13, 1086–1092. [Google Scholar] [CrossRef] [PubMed]
- Minin, I.V.; Minin, O.V.; Shuvalov, G.V. Dielectric wavelength-scaled metalenses based on an anomalous apodization effect for photoconductive optical-to-terahertz switches. In Proceedings of the 2021 XV International Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Novosibirsk, Russia, 19–21 November 2021. accepted. [Google Scholar]
- Gouy, L.G. Sur une propriete nouvelle des ondes lumineuses. C. R. Acad. Sci. Paris 1890, 110, 1251. [Google Scholar]
- Kim, M.; Scharf, T.; Mühlig, S.; Rockstuhl, C.; Herzig, H. Gouy phase anomaly in photonic nanojets. Appl. Phys. Lett. 2011, 98, 191114. [Google Scholar] [CrossRef]
- Bon, P.; Rolly, B.; Bonod, N.; Wenger, J.; Stout, B.; Monneret, S.; Rigneault, H. Imaging the Gouy phase shift in photonic jets with a wavefront sensor. Opt. Lett. 2012, 37, 3531–3533. [Google Scholar] [CrossRef]
- Pham, H.; Hisatake, S.; Minin, I.V.; Minin, O.V.; Nagatsuma, T. Three-dimensional direct observation of Gouy phase shift in a terajet produced by a dielectric cuboid. Appl. Phys. Lett. 2016, 108, 191102. [Google Scholar] [CrossRef]
- Pham, H.; Hisatake, S.; Minin, O.V.; Nagatsuma, T.; Minin, I.V. Asymmetric phase anomaly of terajet generated from dielectric cube under oblique illumination. Appl. Phys. Lett. 2017, 110, 201105. [Google Scholar] [CrossRef]
- Liñares, J.; Prieto-Blanco, X.; Montero-Orille, C.; Moreno, N. Spatial mode multiplexing/demultiplexing by Gouy phase interferometry. Opt. Lett. 2017, 42, 93–96. [Google Scholar]
- Christian, G.; Goubau, J. Experimental studies on a beam waveguide for millimeter waves. IRE Trans. Antennas Propag. 1961, 9, 256. [Google Scholar] [CrossRef]
- Sobel, F.; Wentworth, F.; Wiltse, J. Quasi-Optical Surface Waveguide and Other Components for the 100-to 300-Gc Region. IRE Trans. Microw. Theory Tech. 1961, 9, 512. [Google Scholar]
- Chen, Z.; Taflove, A.; Backman, V. Highly efficient optical coupling and transport phenomena in chains of dielectric microspheres. Opt. Lett. 2006, 31, 389–391. [Google Scholar] [CrossRef]
- Kapitonov, A.; Astratov, V. Observation of nanojet-induced modes with small propagation losses in chains of coupled spherical cavities. Opt. Lett. 2007, 32, 409–411. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Astratov, V. Photonic nanojet-induced modes in chains of size-disordered microspheres with an attenuation of only 0.08 dB per sphere. Appl. Phys. Lett. 2008, 92, 261111. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Pacheco-Peña, V.; Beruete, M. All-dielectric periodic terajet waveguide using an array of coupled cuboids. Appl. Phys. Lett. 2015, 106, 254102. [Google Scholar] [CrossRef]
- Mitsui, T.; Wakayama, Y.; Onodera, T.; Hayashi, T.; Ikeda, N.; Sugimoto, Y.; Takamasu, T.; Oikawa, H. Micro-demultiplexer of Coupled Resonator Optical Waveguide Fabricated by Microspheres. Adv. Mater. 2010, 22, 3022–3026. [Google Scholar] [CrossRef] [PubMed]
- Mitsui, T.; Onodera, Y.; Wakayama, T.; Hayashi, N.; Ikeda, Y.; Sugimoto, T.; Takamasu, H.; Oikawa, H. Influence of micro-joints formed between spheres in coupled resonator optical waveguide. Opt. Express 2011, 19, 22258–22267. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Minin, O.V.; Minin, I.V. Periodical focusing mode achieved through a chain of mesoscale dielectric particles with a refractive index near unity. Opt. Commun. 2019, 434, 110–117. [Google Scholar] [CrossRef]
- Mikaelyan, A. SELFOC dielectric waveguides. Sov. J. Quantum Electron. 1977, 7, 266–267. [Google Scholar] [CrossRef]
- Liu, L.; Rahman, M.; Ning, Y.; Grattan, K. Accurate mode characterization of graded-index multimode fibers for the application of mode-noise analysis. Appl. Opt. 1995, 34, 1540–1543. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Pacheco-Peña, V.; Beruete, M. Localized photonic jets from flat, three-dimensional dielectric cuboids in the reflection mode. Opt. Lett. 2015, 40, 2329–2332. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Kharitoshin, N. Localized High Field Enhancements from Hemispherical 3D Mesoscale Dielectric Particles in the Reflection Mode. In Proceedings of the 2015 16th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices, Novosibirsk, Russia, 29 June–3 July 2015; pp. 331–333. [Google Scholar]
- Minin, I.V.; Minin, O.V.; Nesedov, I. Photonic jets from Babinet’s cuboid structures in the reflection mode. Opt. Lett. 2016, 41, 785–787. [Google Scholar] [CrossRef]
- Yue, L.; Yan, B.; Monks, J.; Dhama, R.; Wang, Z.; Minin, O.V.; Minin, I.V. Photonic Jet by a Near-Unity-Refractive-Index Sphere on a Dielectric Substrate with High Index Contrast. Ann. Phys. 2018, 530, 1800032. [Google Scholar] [CrossRef]
- Minin, I.V.; Geints, Y.; Zemlyanov, A.; Minin, O.V. Specular-reflection photonic nanojet: Physical basis and optical trapping application. Opt. Express 2020, 28, 22690. [Google Scholar] [CrossRef]
- Wang, H.; Wu, X.; Shen, D. Trapping and manipulating nanoparticles in photonic nanojets. Opt. Lett. 2016, 41, 1652. [Google Scholar] [CrossRef]
- Sergeeva, K.; Sergeev, A.; Minin, O.V.; Minin, I.V. A Closer Look at Photonic Nanojets in Reflection Mode: Control of Standing Wave Modulation. Photonics 2021, 8, 54. [Google Scholar] [CrossRef]
- Minin, I.V.; Liu, C.; Yang, Y.; Staliunas, K.; Minin, O.V. Experimental observation of flat focusing mirror based on photonic jet effect. Sci. Rep. 2020, 10, 8459. [Google Scholar] [CrossRef]
- Cheng, Y.; Kicas, S.; Trull, J.M.; Peckus, C.; Cojocaru, R.; Vilaseca, R. Drazdys & K. Staliunas. Flat Focusing Mirror. Sci. Rep. 2014, 4, 6326. [Google Scholar] [PubMed]
- Cheng, Y.; Staliunas, K. Near-field flat focusing mirrors. Appl. Phys. Rev. 2018, 5, 11101. [Google Scholar] [CrossRef]
- Zhou, S.; Deng, Y.; Zhou, W.; Yu, M.; Urbach, H.; Wu, Y. Effects of whispering gallery mode in microsphere super-resolution imaging. Appl. Phys. B 2017, 123, 236. [Google Scholar] [CrossRef]
- Hoang, T.; Duan, Y.; Chen, X.; Barbastathis, G. Focusing and imaging in microsphere-based microscopy. Opt. Express 2015, 23, 12337–12353. [Google Scholar] [CrossRef] [PubMed]
- Geints, Y.; Panina, E.; Minin, I.V.; Minin, O.V. Study of focusing parameters of wavelength-scale binary phase Fresnel zone plate. J. Opt. 2021, 23, 65101. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Terahertz artificial dielectric cuboid lens on substrate for super-resolution images. Opt. Quant. Electron. 2017, 49, 326. [Google Scholar] [CrossRef]
- Liu, C.; Yen, T.; Minin, O.V.; Minin, I.V. Engineering photonic nanojet by a graded-index micro-cuboid. Phys. E. Low-Dimens. Syst. Nanostructures 2018, 98, 105–110. [Google Scholar] [CrossRef]
- Kwon, S.; Kim, K.; Park, J.; Cho, Y.; Lee, M. Microsphere-assisted ultra-small spot spectral reflectometry technique for semiconductor device metrology. Proc. SPIE 2021, 11611, 116110G. [Google Scholar]
- Minin, I.V.; Minin, O.V.; Cao, Y.; Yan, B.; Wang, Z.; Luk’yanchuk, B. Photonic Lenses with whisphering Gallery Waves at Janus Particles. arXiv 2020, arXiv:2012.09489. [Google Scholar]
- de Gennes, P.-G. Soft Matter (Nobel Lecture). Angew. Chem. Int. Ed. Engl. 1992, 31, 842–845. [Google Scholar] [CrossRef]
- Mason, D.; Jouravlev, M.; Kim, S. Enhanced resolution beyond the Abbe diffraction limit with wavelength-scale solid immersion lenses. Opt. Lett. 2010, 35, 2007–2009. [Google Scholar] [CrossRef]
- Kino, G.; Mansfield, S. Near field and solid immersion optical microscope. US Patent 5,004,307, 2 April 1991. [Google Scholar]
- Yu, N.; Genevet, P.; Kats, M.; Aieta, F.; Tetienne, J.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Pham, H.; Hisatake, S.; Minin, O.V.; Nagatsuma, T.; Minin, I.V. Enhancement of Spatial Resolution of Terahertz Imaging Systems Based on Terajet Generation by Dielectric Cube. APL Photonics 2017, 2, 56106. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Salvador-Sanchez, J.; Delgado-Notario, J.; Calvo-Gallego, J.; Baranov, P.; Ferrando-Bataller, M.; Fobelets, K.; Velazquez-Perez, J.; Meziani, Y. Imaging resolution enhancement using terajet effect at 0.3THz. Proc. SPIE 2021, 11868, 118680N. [Google Scholar]
- Minin, I.V.; Minin, O.V. Terahertz Microscopy with Oblique Subwavelength Illumination in near Field. Preprints 2021, 2021, 90024. [Google Scholar] [CrossRef]
- Abbe, E. On the estimation of the aperture of the microscope. J. Roy Microscop. Soc. Ser. II 1881, 1, 349–388. [Google Scholar] [CrossRef]
- Sanchez, C.; Cristobal, G.; Bueno, G.; Blanco, S.; Borrego-Ramos, M.; Olenici, A.; Pedraza, A.; Ruiz-Santaquiteria, J. Oblique illumination in microscopy: A quantitative evaluation. Micron 2018, 105, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Minin, I.V.; Minin, O.V. THz microscopy with oblique subwavelength illumination: Proof of concept. Quantum Electron. 2022. accepted. [Google Scholar]
- Cao, Y.; Liu, Z.; Minin, O.V.; Minin, I.V. Deep Subwavelength-Scale Light Focusing and Confinement in Nanohole-Structured Mesoscale Dielectric Spheres. Nanomaterials 2019, 9, 186. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Cao, Y.; Liu, Z.; Geints, Y.E.; Karabchevsky, A. Optical vacuum cleaner by optomechanical manipulation of nanoparticles using nanostructured mesoscale dielectric cuboid. Sci. Rep. 2019, 9, 12748. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Ultrafast all-optical THz modulation based on wavelength scaled dielectric particle with graphene monolayer. Proc. SPIE 2019, 11065, 110651J. [Google Scholar]
- Minin, O.V.; Minin, I.V.; Cao, Y. Optical magnet for nanoparticles manipulations based on optical vacuum cleaner concept. Proc. SPIE 2021, 11845, 118451G. [Google Scholar]
- Zhou, Y.; Hong, M. Formation of a three-dimensional bottle beam via an engineered microsphere. Photonics Res. 2021, 9, 1598. [Google Scholar] [CrossRef]
- Dholakia, K.; Bruce, G. Optical hooks. Nat. Photonics 2019, 13, 229. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Recent Trends in Optical Manipulation Inspired by Mesoscale Photonics and Diffraction Optics. J. Biomed. Photonics Eng. 2020, 6, 20301. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Device for forming the optical trap in the form of the photonic hook. Patent of Russia 161207, 27 October 2015. [Google Scholar]
- Yue, L.; Minin, O.V.; Wang, Z.; Monks, J.; Snalin, A.; Minin, I.V. Photonic hook: A new curved light beam. Opt. Lett. 2018, 43, 771. [Google Scholar] [CrossRef]
- Spector, M.; Ang, A.; Minin, O.V.; Minin, I.V.; Karabchevsky, A. Temperature mediated ’Photonic hook’ nanoparticle manipulator with pulsed illumination. Nanoscale Adv. 2020, 2, 2595–2601. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. The Photonic Hook: From Optics to Acoustics and Plasmonics; Springer: Cham, Germany, 2021. [Google Scholar]
- Minin, I.V.; Minin, O.V.; Katyba, G.; Chernomyrdin, N.; Zaytsev, K.; Yue, L.; Wang, Z.; Christodoulides, D.N. Experimental observation of a photonic hook. APL 2019, 114, 31105. [Google Scholar] [CrossRef]
- Spector, M.; Ang, A.; Minin, O.V.; Minin, I.V.; Karabchevsky, A. Photonic hook formation in near-infrared with MXene Ti3C2 nanoparticles. Nanoscale Adv. 2020, 2, 5312–5318. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Dielectric particle-based strategy to design a new self-bending subwavelength structured light beams. IOP Conf. Series Mater. Sci. Eng. 2021, 1019, 12093. [Google Scholar] [CrossRef]
- Geints, Y.; Minin, I.V.; Minin, O.V. Tailoring ‘photonic hook’ from Janus dielectric microbar. J. Opt. 2020, 22, 65606. [Google Scholar] [CrossRef]
- Gu, G.; Zhang, P.; Chen, S.; Zhang, Y.; Yang, H. Inflection point: A perspective on photonic nanojets. Photonics Res. 2021, 9, 1157. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Liu, C.; Wei, H.; Geints, Y.; Karabchevsky, A. Experimental demonstration of tunable photonic hook by partially illuminated dielectric microcylinder. Opt. Lett. 2020, 45, 4899. [Google Scholar] [CrossRef]
- Liu, C.; Chung, H.; Minin, O.V.; Minin, I.V. Shaping photonic hook via well-controlled illumination of finite-size graded-index micro-ellipsoid. J. Opt. 2020, 22, 85002. [Google Scholar] [CrossRef]
- Pacheco-Peña, V.; Riley, J.; Liu, C.; Minin, O.V.; Minin, I.V. Diffraction limited photonic hook via scattering and diffraction of dual-dielectric structures. Sci. Rep. 2021, 11, 20278. [Google Scholar] [CrossRef] [PubMed]
- Ang, A.; Karabchevsky, A.; Minin, I.V.; Minin, O.V.; Sukhov, S.; Snalin, A. ‘Photonic Hook’ based optomechanical nanoparticle manipulator. Sci. Rep. 2018, 8, 2029. [Google Scholar] [CrossRef]
- Ang, A.; Minin, I.V.; Minin, O.V.; Sukhov, S.; Snalin, A.; Karabchevsky, A. Low-contrast photonic hook manipulator for cellular differentiation. In Proceedings of the 9th International Conference on Metamaterials, Photonic Crystals and Plasmonics, META 2018, Marseille, France, 24 June–1 July 2018. [Google Scholar]
- Cipolla, M.J. Barriers of the CNS. In The Cerebral Circulation. San Rafael (CA): Morgan & Claypool Life Sciences; NCBI: Bethesda, ML, USA, 2009; Chapter 6. Available online: www.ncbi.nlm.nih.gov/books/NBK53084/ (accessed on 15 December 2021).
- Minin, I.V.; Minin, O.V.; Liu, Y.; Tuchin, V.; Liu, C. Concept of Photonic Hook Scalpel Generated by Shaped Fiber Tip with Asymmetric Radiation. J. Biophotonics 2021, 14, e202000342. [Google Scholar] [CrossRef] [PubMed]
- Geints, Y.; Minin, O.V.; Yue, L.; Minin, I.V. Wavelength-scale photonic space switch proof-of-concept based on photonic hook effect. Ann. Phys. 2021, 533, 2100192. [Google Scholar] [CrossRef]
- Minin, I.V.; Shuvalov, G.V.; Minin, O.V. All-dielectric asymmetrical metasurfaces based on mesoscale dielectric particles with different optical transmissions in opposite directions through full internal reflection. In Frontier Research and Innovation in Optoelectronics Technology and Industry; CRC Press: Kunming, China, 2018; pp. 437–440. [Google Scholar]
- Liu, C.-Y.; Minin, O.V.; Minin, I.V. First experimental observation of array of photonic jets from saw-tooth phase diffraction grating. EPL Europhys. Lett. 2018, 123, 54003. [Google Scholar] [CrossRef]
- Ge, S.; Liu, W.; Zhang, J.; Huang, Y.; Xi, Y.; Yang, P.; Sun, X.; Li, S.; Lin, D.; Zhou, D.; et al. Novel Bilayer Micropyramid Structure Photonic Nanojet for Enhancing a Focused Optical Field. Nanomaterials 2021, 11, 2034. [Google Scholar] [CrossRef]
- Balezin, M.; Baryshnikova, K.V.; Kapitanova, P.; Evlyukhin, A. Electromagnetic properties of the Great Pyramid: First multipole resonances and energy concentration. J. Appl. Phys. 2018, 124, 34903. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Yue, L. Electromagnetic properties of Pyramids from positions of photonics. Russ. Phys. J. 2020, 62, 1763–1769. [Google Scholar] [CrossRef]
- Schuller, J.; Barnard, E.; Cai, W.; Jun, Y.; White, J.; Brongersma, M. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zhang, J.; Liu, Y. Light manipulation with encoded plasmonic nanostructures. EPJ Appl. Metamaterials 2014, 1, 6. [Google Scholar] [CrossRef][Green Version]
- Ju, D.; Pei, H.; Jiang, Y.; Sun, Y. Controllable and enhanced nanojet effects excited by surface plasmon polariton. Appl. Phys. Lett. 2013, 102, 171109. [Google Scholar] [CrossRef]
- Pacheco-Pena, V.; Minin, I.V.; Minin, O.V.; Beruete, M. Comprehensive analysis of photonic nanojets in 3D dielectric cuboids excited by surface plasmons. Ann. Phys. 2016, 528, 684. [Google Scholar] [CrossRef]
- Pacheco-Pena, V.; Minin, I.V.; Minin, O.V.; Beruete, M. Increasing Surface Plasmons Propagation via Photonic Nanojets with Periodically Spaced 3D Dielectric Cuboids. Photonics 2016, 3, 10. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Glinskiy, I.; Malureanu, R.; Lavrinenko, A.; Yakubovsky, D.; Volcov, V.; Ponomarev, D. Plasmonic nanojet: An experimental demonstration. Opt. Lett. 2020, 45, 3244–3247. [Google Scholar] [CrossRef]
- Caldwell, J.; Lindsay, L.; Giannini, V.; Vurgaftman, I.; Reinecke, T.; Maier, S.; Glembocki, O. Low-loss, infrared and terahertz nanophotonics using surface phonon polaritons. Nanophotonics 2015, 4, 44–68. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Ponomarev, D.; Glinskiy, I. Photonic hook plasmons: A new curved surface wave. Ann. Phys. 2018, 530, 1800359. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Glinskiy, I.; Malureanu, R.; Lavrinenko, A.; Yakubovsky, D.; Volcov, V.; Ponomarev, D. Experimental verification of a plasmonic hook in a dielectric Janus particle. APL 2021, 118, 131107. [Google Scholar] [CrossRef]
- Zhang, Y.; Min, C.; Dou, X.; Wang, X.; Urbach, H.; Somekh, M.; Yuan, X. Plasmonic tweezers: For nanoscale optical trapping and beyond. Light Sci. Appl. 2021, 10, 59. [Google Scholar] [CrossRef]
- Minin, O.V.; Minin, I.V. Acoustojet: Acoustic analogue of photonic jet phenomenon based on penetrable 3D particle. Opt. Quantum Electron. 2017, 49, 54. [Google Scholar] [CrossRef]
- Lopes, J.; Andrade, M.; Leao-Neto, J.; Adamowski, J.; Minin, I.V.; Silva, G. Focusing acoustic beams with a ball shaped lens beyond the diffraction limit. Phys. Rev. Appl. 2017, 8, 24013. [Google Scholar] [CrossRef]
- Minin, O.V.; Minin, I.V. Mesoscale acoustical cylindrical superlens. MATEC Web Conf. 2018, 155, 1029. [Google Scholar] [CrossRef]
- Tarrazo-Serrano, D.; Rubio, C.; Minin, O.V.; Uris, A.; Minin, I.V. Ultrasonic focusing with mesoscale polymer cuboid. Ultrasonics 2020, 106, 106143. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Horiuchi, T.; Yu, M. Broadband ultra-long acoustic jet based on double-foci Luneburg lens. JASA Express Lett. 2021, 1, 114001. [Google Scholar] [CrossRef]
- Rubio, C.; Tarrazo-Serrano, D.; Minin, O.V.; Uris, A.; Minin, I.V. Enhancement of pupil masked wavelength-scale gas-filled flat acoustic lens based on anomaly apodization effect. Phys. Lett. A 2019, 383, 396–399. [Google Scholar] [CrossRef]
- Lu, C.; Yu, R.; Wang, K.; Wang, J.; and Wu, D. Tunable acoustic jet generated by a masked cylindrical lens. Appl. Phys. Express 2020, 13, 97003. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Tseplyaev, I. The relationship between resonance scattering and the formation of an acoustojet under the interaction of ultrasound with a dielectric sphere immersed in water. J. Phys. Conf. Ser. 2017, 881, 12025. [Google Scholar] [CrossRef]
- Rubio, C.; Minin, I.V.; Uris, A.; Minin, O.V. Super-resonances in a dielectric mesoscale sphere immersed in water: Effects in extreme field localization of acoustic wave. Proc. Mtgs. Acoust. 2019, 38, 70001. [Google Scholar]
- Rubio, C.; Tarrazo-Serrano, D.; Minin, O.V.; Uris, A.; Minin, I.V. Acoustical hooks: A new subwavelength self-bending beam. Results Phys. 2020, 16, 102921. [Google Scholar] [CrossRef]
- Ren, X.; Zhou, Q.; Xu, Z.; Liu, X. Acoustic hook beam lens for particle trapping. Appl. Phys. Express 2020, 13, 64003. [Google Scholar] [CrossRef]
- Castiñeira-Ibáñez, S.; Tarrazó-Serrano, D.; Uris, A.; Rubio, C.; Minin, O.V.; Minin, I.V. Cylindrical 3D printed configurable ultrasonic lens for subwavelength focusing enhancement. Sci. Rep. 2020, 10, 20279. [Google Scholar] [CrossRef]
- Castiñeira-Ibáñez, S.; Tarrazó-Serrano, D.; Uris, A.; Rubio, C. Tunable acoustic hooks from Janus cylinder. Results Phys. 2021, 24, 104134. [Google Scholar] [CrossRef]
- Sarvazyan, A.; Urban, M.; Greenleaf, J. Acoustic waves in medical imaging and diagnostics. Ultrasound Med. Biol. 2013, 39, 1133–1146. [Google Scholar] [CrossRef] [PubMed]
- Gorgin, R.; Luo, Y.; Wu, Z. Environmental and operational conditions effects on Lamb wave based structural health monitoring systems: A review. Ultrasonics 2020, 105, 106114. [Google Scholar] [CrossRef]
- Wang, J.; Yurchenko, D.; Hu, G.; Zhao, L.; Tang, L.; Yang, Y. Perspectives in flow-induced vibration energy harvesting. Appl. Phys. Lett. 2021, 119, 100502. [Google Scholar] [CrossRef]
- Taylor, M.A.; Waleed, M.; Stilgoe, A.B.; Rubinsztein-Dunlop, H.; Bowen, W.P. Enhanced optical trapping via structured scattering. Nat. Photon. 2015, 9, 669–673. [Google Scholar] [CrossRef]
- Dholakia, K.; Čižmár, T. Shaping the future of manipulation. Nat. Photon. 2011, 5, 335–342. [Google Scholar] [CrossRef]
- Long, L.; Chen, J.; Yu, H.; Li, Z.Y. Strong optical force of a molecule enabled by the plasmonic nanogap hot spot in a tip-enhanced Raman spectroscopy system. Photon. Res. 2020, 8, 1573–1579. [Google Scholar] [CrossRef]
- Shi, L.; Meseguer, F. Magnetic interaction in all silicon waveguide spherical coupler device. Opt. Express. 2012, 20, 22616–22626. [Google Scholar] [CrossRef] [PubMed]
- Rastinehad, A.; Anastos, H.; Wajswol, E.; Winoker, J.S.; Sfakianos, J.P.; Doppalapudi, S.K.; Carrick, M.R.; Knauer, C.J.; Taouli, B.; Lewis, S.C.; et al. Gold nanoshell-localized photothermal ablation of prostate tumors in a clinical pilot device study. PNAS 2019, 116, 18590–18596. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, Y.; Zhou, R.; Hong, M. Microsphere—Toward Future of Optical Microscopes. iScience 2020, 23, 101211. [Google Scholar] [CrossRef]
- Savo, R.; Morandi, A.; Muller, J.S.; Kaufmann, F.; Timpu, F.; Escale, M.R.; Zanini, M.; Isa, L.; Grange, R. Broadband Mie driven random quasi-phasematching. Nat. Photonics 2020, 14, 740–747. [Google Scholar] [CrossRef]
- Huang, K.; Ye, H.; Teng, J.; Yeo, S.P.; Luk’yanchuk, B.; Qiu, C.W. Optimization-free superoscillatory lens using phase and amplitude masks. Laser Photonics Rev. 2014, 8, 152–157. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Control of focusing properties of diffraction elements. Sov. J. Quantum. Electron. 1990, 20, 198–199. [Google Scholar] [CrossRef]
- Mahariq, I.; Giden, I.; Minin, I.V.; Minin, O.V.; Kurt, H. Strong electromagnetic field localization near the surface of hemicylindrical particles. Opt. Quant. Electron. 2017, 49, 423. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Eremeev, A.; Tseplyaev, I. Spherical and cylindrical particle resonator as a cloak system. IOP Conf. Series Mater. Sci. Eng. 2018, 363, 12026. [Google Scholar] [CrossRef]
- Sugathan, B.; Nilaya, J.P.; Pillai, V.; Biswas, D.J. Particle assisted structuring on metallic substrate: Anomaly when particle size exceeds irradiation wavelength. AIP Adv. 2020, 10, 35222. [Google Scholar] [CrossRef]
- Kravtsov, Y.A.; Orlov, Y.I. Limits of applicability of the method of geometric optics and related problems. Sov. Phys. Usp. 1980, 23, 750. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minin, O.V.; Minin, I.V. Optical Phenomena in Mesoscale Dielectric Particles. Photonics 2021, 8, 591. https://doi.org/10.3390/photonics8120591
Minin OV, Minin IV. Optical Phenomena in Mesoscale Dielectric Particles. Photonics. 2021; 8(12):591. https://doi.org/10.3390/photonics8120591
Chicago/Turabian StyleMinin, Oleg V., and Igor V. Minin. 2021. "Optical Phenomena in Mesoscale Dielectric Particles" Photonics 8, no. 12: 591. https://doi.org/10.3390/photonics8120591
APA StyleMinin, O. V., & Minin, I. V. (2021). Optical Phenomena in Mesoscale Dielectric Particles. Photonics, 8(12), 591. https://doi.org/10.3390/photonics8120591





