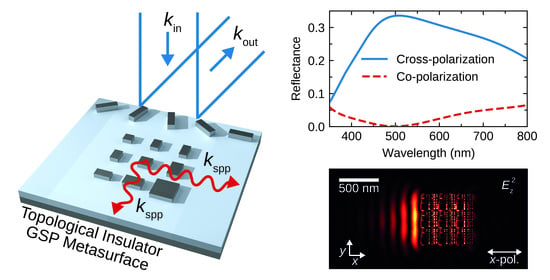
Topological-Insulator-Based Gap-Surface Plasmon Metasurfaces
Abstract
:1. Introduction
2. Results and Discussion
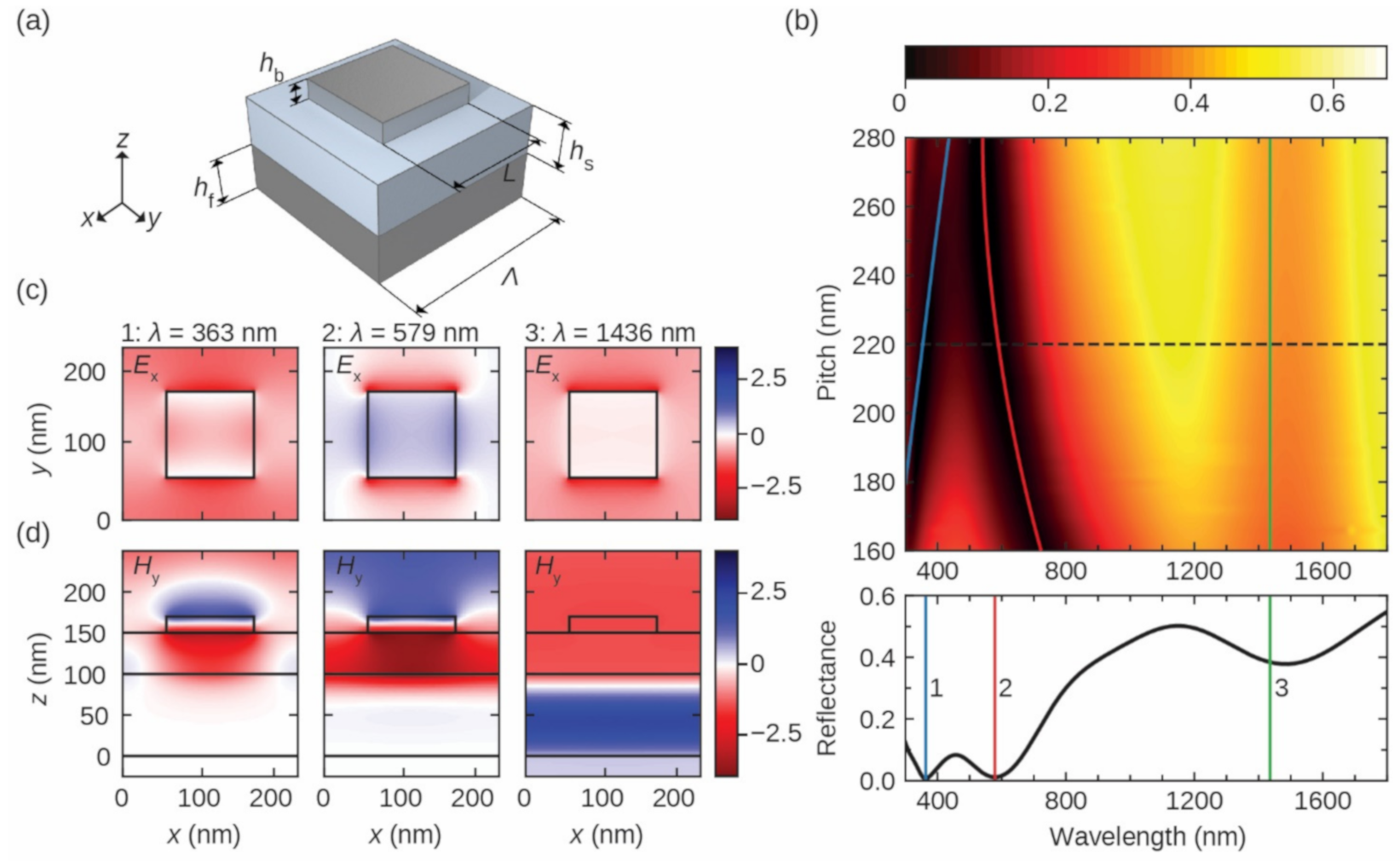
2.1. TI-Based GSP Metasurface
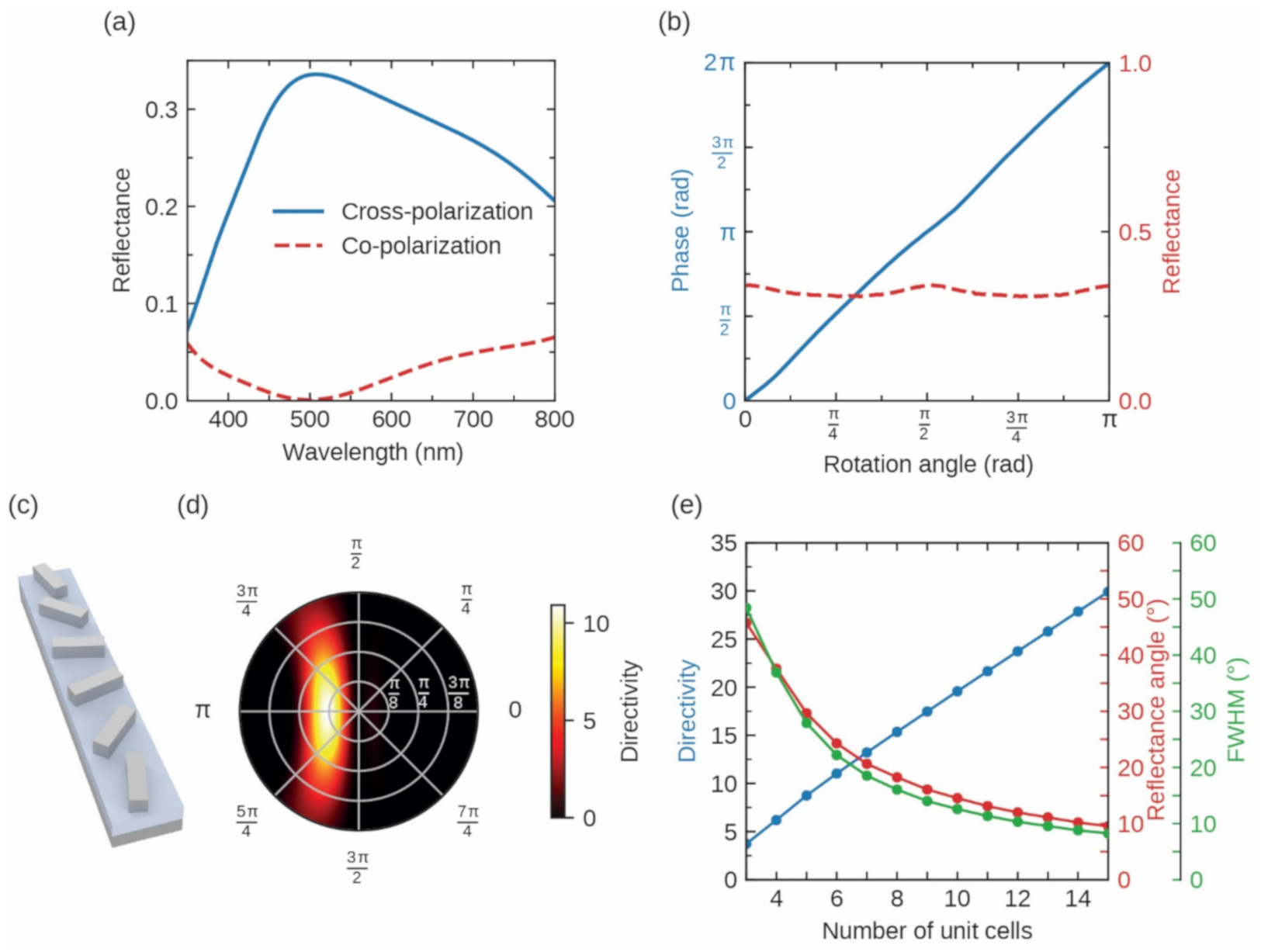
2.2. Far-Field Functionalities
2.3. Near-Field Functionalities
3. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A





References
- Yu, N.; Genevet, P.; Kats, M.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [Green Version]
- Park, J.H.; Ndao, A.; Cai, W.; Hsu, L.; Kodigala, A.; Lepetit, T.; Lo, Y.H.; Kanté, B. Symmetry-breaking-induced plasmonic exceptional points and nanoscale sensing. Nat. Phys. 2020, 16, 462–468. [Google Scholar] [CrossRef]
- Chanda, D.; Shigeta, K.; Gupta, S.; Cain, T.; Carlson, A.; Mihi, A.; Baca, A.J.; Bogart, G.R.; Braun, P.; Rogers, J.A. Large-area flexible 3D optical negative index metamaterial formed by nanotransfer printing. Nat. Nanotechnol. 2011, 6, 402–407. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Gu, M. Angular Momentum-Reversible Near-Unity Bisignate Circular Dichroism. Laser Photonics Rev. 2018, 12, 1–6. [Google Scholar] [CrossRef]
- Etchegoin, P.G.; le Ru, E.C.; Meyer, M. An analytic model for the optical properties of gold. J. Chem. Phys. 2006, 125. [Google Scholar] [CrossRef] [PubMed]
- Felser, C.; Qi, X.L. Topological insulators. Mrs Bull. 2014, 39, 843–846. [Google Scholar] [CrossRef] [Green Version]
- Pesin, D.; MacDonald, A.H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mater. 2012, 11, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Di Pietro, P.; Ortolani, M.; Limaj, O.; Di Gaspare, A.; Giliberti, V.; Giorgianni, F.; Brahlek, M.; Bansal, N.; Koirala, N.; Oh, S.; et al. Observation of Dirac plasmons in a topological insulator. Nat. Nanotechnol. 2013, 8, 556–560. [Google Scholar] [CrossRef] [Green Version]
- Ginley, T.P.; Law, S. Coupled Dirac Plasmons in Topological Insulators. Adv. Opt. Mater. 2018, 6, 1–5. [Google Scholar] [CrossRef]
- Stauber, T. Plasmonics in Dirac systems: From graphene to topological insulators. J. Phys. Condens. Matter 2014, 26. [Google Scholar] [CrossRef]
- Ginley, T.; Wang, Y.; Wang, Z.; Law, S. Dirac plasmons and beyond: The past, present, and future of plasmonics in 3D topological insulators. Mrs Commun. 2018, 8, 782–794. [Google Scholar] [CrossRef]
- Lai, Y.P.; Lin, I.T.; Wu, K.H.; Liu, J.M. Plasmonics in topological insulators. Nanomater. Nanotechnol. 2014, 4, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Stauber, T.; Gómez-Santos, G.; Brey, L. Plasmonics in Topological Insulators: Spin-Charge Separation, the Influence of the Inversion Layer, and Phonon-Plasmon Coupling. Acs Photonics 2017, 4, 2978–2988. [Google Scholar] [CrossRef]
- Autore, M.; D’Apuzzo, F.; di Gaspare, A.; Giliberti, V.; Limaj, O.; Roy, P.; Brahlek, M.; Koirala, N.; Oh, S.; García de Abajo, F.J.; et al. Plasmon-Phonon Interactions in Topological Insulator Microrings. Adv. Opt. Mater. 2015, 3, 1257–1263. [Google Scholar] [CrossRef]
- In, C.; Sim, S.; Kim, B.; Bae, H.; Jung, H.; Jang, W.; Son, M.; Moon, J.; Salehi, M.; Seo, S.Y.; et al. Control over Electron-Phonon Interaction by Dirac Plasmon Engineering in the Bi2Se3 Topological Insulator. Nano Lett. 2018, 18, 734–739. [Google Scholar] [CrossRef]
- Tang, W.; Politano, A.; Guo, C.; Guo, W.; Liu, C.; Wang, L.; Chen, X.; Lu, W. Ultrasensitive Room-Temperature Terahertz Direct Detection Based on a Bismuth Selenide Topological Insulator. Adv. Funct. Mater. 2018, 28, 1–9. [Google Scholar] [CrossRef]
- Viti, L.; Coquillat, D.; Politano, A.; Kokh, K.A.; Aliev, Z.S.; Babanly, M.B.; Tereshchenko, O.E.; Knap, W.; Chulkov, E.V.; Vitiello, M.S. Plasma-Wave Terahertz Detection Mediated by Topological Insulators Surface States. Nano Lett. 2016, 16, 80–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Politano, A.; Silkin, V.M.; Nechaev, I.A.; Vitiello, M.S.; Viti, L.; Aliev, Z.S.; Babanly, M.B.; Chiarello, G.; Echenique, P.M.; Chulkov, E.V. Interplay of surface and Dirac plasmons in topological insulators: The case of Bi2Se3. Phys. Rev. Lett. 2015, 115, 1–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sim, S.; Jang, H.; Koirala, N.; Brahlek, M.; Moon, J.; Sung, J.H.; Park, J.; Cha, S.; Oh, S.; Jo, M.H.; et al. Ultra-high modulation depth exceeding 2400% in optically controlled topological surface plasmons. Nat. Commun. 2015, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Krishnamoorthy, H.N.S.; Adamo, G.; Yin, J.; Savinov, V.; Zheludev, N.I.; Soci, C. Infrared dielectric metamaterials from high refractive index chalcogenides. Nat. Commun. 2020, 11, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Toudert, J.; Serna, R. Interband transitions in semi-metals, semiconductors, and topological insulators: A new driving force for plasmonics and nanophotonics [Invited]. Opt. Mater. Express 2017, 7, 2299. [Google Scholar] [CrossRef]
- Yue, Z.; Cai, B.; Wang, L.; Wang, X.; Gu, M. Intrinsically core-shell plasmonic dielectric nanostructures with ultrahigh refractive index. Sci. Adv. 2016, 2, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, J.; Krishnamoorthy, H.N.S.; Adamo, G.; Dubrovkin, A.M.; So, J.K.; Chong, Y.; Zheludev, N.I.; Soci, C. Plasmonics of topological insulators at optical frequencies. Opt. Infobase Conf. Pap. 2017, e425–e428. [Google Scholar] [CrossRef]
- Dubrovkin, A.M.; Adamo, G.; Yin, J.; Wang, L.; Soci, C.; Wang, Q.J.; Zheludev, N.I. Visible Range Plasmonic Modes on Topological Insulator Nanostructures. Adv. Opt. Mater. 2017, 5, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Yue, Z.; Ren, H.; Wei, S.; Lin, J.; Gu, M. Angular-momentum nanometrology in an ultrathin plasmonic topological insulator film. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Yue, Z.; Xue, G.; Liu, J.; Wang, Y.; Gu, M. Nanometric holograms based on a topological insulator material. Nat. Commun. 2017, 8, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Ou, J.Y.; So, J.K.; Adamo, G.; Sulaev, A.; Wang, L.; Zheludev, N.I. Ultraviolet and visible range plasmonics in the topological insulator Bi1.5Sb0.5Te1.8Se1.2. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Ding, F.; Yang, Y.; Deshpande, R.A.; Bozhevolnyi, S.I. A review of gap-surface plasmon metasurfaces: Fundamentals and applications. Nanophotonics 2018, 7, 1129–1156. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.C.; Lai, Y.C.; Chu, C.H.; Chen, J.W.; Lu, S.H.; Chen, J.; Xu, B.; Kuan, C.H.; et al. Broadband achromatic optical metasurface devices. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Qin, L.; Wu, S.; Deng, J.; Li, L.; Li, X. Tunable light absorbance by exciting the plasmonic gap mode for refractive index sensing. Opt. Lett. 2018, 43, 1427. [Google Scholar] [CrossRef] [PubMed]
- Pors, A.; Nielsen, M.G.; Bernardin, T.; Weeber, J.C.; Bozhevolnyi, S.I. Efficient unidirectional polarization-controlled excitation of surface plasmon polaritons. Light Sci. Appl. 2014, 3, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Palacios, E.; Butun, S.; Aydin, K. Visible-frequency metasurfaces for broadband anomalous reflection and high-efficiency spectrum splitting. Nano Lett. 2015, 15, 1615–1621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Werner, W.S.M.; Glantschnig, K.; Ambrosch-Draxl, C. Optical constants and inelastic electron-scattering data for 17 elemental metals. J. Phys. Chem. Ref. Data 2009, 38, 1013–1092. [Google Scholar] [CrossRef]
- Vries, d.; Kornelis, E. Taking Topological Insulators for a Spin: Towards Understanding of Spin and Charge Transport in Bi2Se3; Rijksuniversiteit Groningen: Groningen, The Netherlands, 2017. [Google Scholar]
- Sarnet, T.; Hatanpää, T.; Puukilainen, E.; Mattinen, M.; Vehkamäki, M.; Mizohata, K.; Ritala, M.; Leskelä, M. Atomic layer deposition and characterization of Bi2Te3 thin films. J. Phys. Chem. A 2015, 119, 2298–2306. [Google Scholar] [CrossRef]
- Giani, A.; Boulouz, A.; Pascal-Delannoy, F.; Foucaran, A.; Charles, E.; Boyer, A. Growth of Bi2Te3 and Sb2Te3 thin films by MOCVD. Mater. Sci. Eng. B Solid State Mater. Adv. Technol. 1999, 64, 19–24. [Google Scholar] [CrossRef]
- Lucarini, V.; Saarinen, J.J.; Peiponen, K.E.; Vartiainen, E.M. Kramers-Kronig Relations in Optical Materials Research; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Dastmalchi, B.; Tassin, P.; Koschny, T.; Soukoulis, C.M. A New Perspective on Plasmonics: Confinement and Propagation Length of Surface Plasmons for Different Materials and Geometries. Adv. Opt. Mater. 2016, 4, 177–184. [Google Scholar] [CrossRef]
- Pors, A.; Bozhevolnyi, S.I. Plasmonic metasurfaces for efficient phase control in reflection. Opt. Express 2013, 21, 27438. [Google Scholar] [CrossRef]
- Pors, A.; Bozhevolnyi, S.I. Efficient and broadband quarter-wave plates by gap-plasmon resonators. Opt. Express 2013, 21, 2942. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Raether, H.; Hohler, G.; Niekisch, E.A. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar] [CrossRef]
- Chen, H.T.; Taylor, A.J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79. [Google Scholar] [CrossRef] [Green Version]
- Pors, A.; Albrektsen, O.; Radko, I.P.; Bozhevolnyi, S.I. Gap plasmon-based metasurfaces for total control of reflected light. Sci. Rep. 2013, 3, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, Q.; Jin, G.; Cao, L. When metasurface meets hologram: Principle and advances. Adv. Opt. Photonics 2019, 11, 518. [Google Scholar] [CrossRef]
- Mueller, J.P.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett. 2017, 118, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Xiao, S.; He, Q.; Sun, S.; Zhou, L. Photonic Spin Hall Effect with Nearly 100% Efficiency. Adv. Opt. Mater. 2015, 3, 1102–1108. [Google Scholar] [CrossRef]
- Hasman, E.; Kleiner, V.; Biener, G.; Niv, A. Phase Optics: Formation of Pancharatnam- Berry Phase Optical Elements With Space-Variant Subwavelength Gratings. Opt. Photonics News 2002, 13, 45. [Google Scholar] [CrossRef]
- Meng, C.; Tang, S.; Ding, F.; Bozhevolnyi, S.I. Optical Gap-Surface Plasmon Metasurfaces for Spin-Controlled Surface Plasmon Excitation and Anomalous Beam Steering. ACS Photonics 2020, 7, 1849–1856. [Google Scholar] [CrossRef]
- Miao, Z.; Wu, Q.; Li, X.; He, Q.; Ding, K.; An, Z.; Zhang, Y.; Zhou, L. Widely tunable terahertz phase modulation with gate-controlled graphene metasurfaces. Phys. Rev. X 2015, 5, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Cong, L.; Pitchappa, P.; Lee, C.; Singh, R. Active Phase Transition via Loss Engineering in a Terahertz MEMS Metamaterial. Adv. Mater. 2017, 29. [Google Scholar] [CrossRef]
- Qu, C.; Ma, S.; Hao, J.; Qiu, M.; Li, X.; Xiao, S.; Miao, Z.; Dai, N.; He, Q.; Sun, S.; et al. Tailor the Functionalities of Metasurfaces Based on a Complete Phase Diagram. Phys. Rev. Lett. 2015, 115, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Schinke, C.; Christian, P.P.; Schmidt, J.; Brendel, R.; Bothe, K.; Vogt, M.R.; Kröger, I.; Winter, S.; Schirmacher, A.; Lim, S.; et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. Aip Adv. 2015, 5. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aigner, A.; Maier, S.A.; Ren, H. Topological-Insulator-Based Gap-Surface Plasmon Metasurfaces. Photonics 2021, 8, 40. https://doi.org/10.3390/photonics8020040
Aigner A, Maier SA, Ren H. Topological-Insulator-Based Gap-Surface Plasmon Metasurfaces. Photonics. 2021; 8(2):40. https://doi.org/10.3390/photonics8020040
Chicago/Turabian StyleAigner, Andreas, Stefan A. Maier, and Haoran Ren. 2021. "Topological-Insulator-Based Gap-Surface Plasmon Metasurfaces" Photonics 8, no. 2: 40. https://doi.org/10.3390/photonics8020040
APA StyleAigner, A., Maier, S. A., & Ren, H. (2021). Topological-Insulator-Based Gap-Surface Plasmon Metasurfaces. Photonics, 8(2), 40. https://doi.org/10.3390/photonics8020040