The Overlap Factor Model of Spin-Polarised Coupled Lasers
Abstract
1. Introduction
Summary Overview of the Paper
- Section 2: derivation of the general model for the dynamics of arrays of coupled, spin-polarised lasers;
- Section 3: discussion of the ‘overlap factors’, which incorporate the details of the geometry of the arrays;
- Section 4: specialisation to a double-guided structure and demonstration that the model reduces to both the spin-flip model and coupled mode model in the appropriate limit;
- Section 5: discussion of steady state solutions, giving exact and approximate expressions;
- Section 6: numerical solutions, illustrating spatial profiles for the optical ellipticity and stability boundaries; and,
- Section 7: conclusions.
2. The General Model
2.1. The Optical Rate Equations
2.2. The Carrier Rate Equations
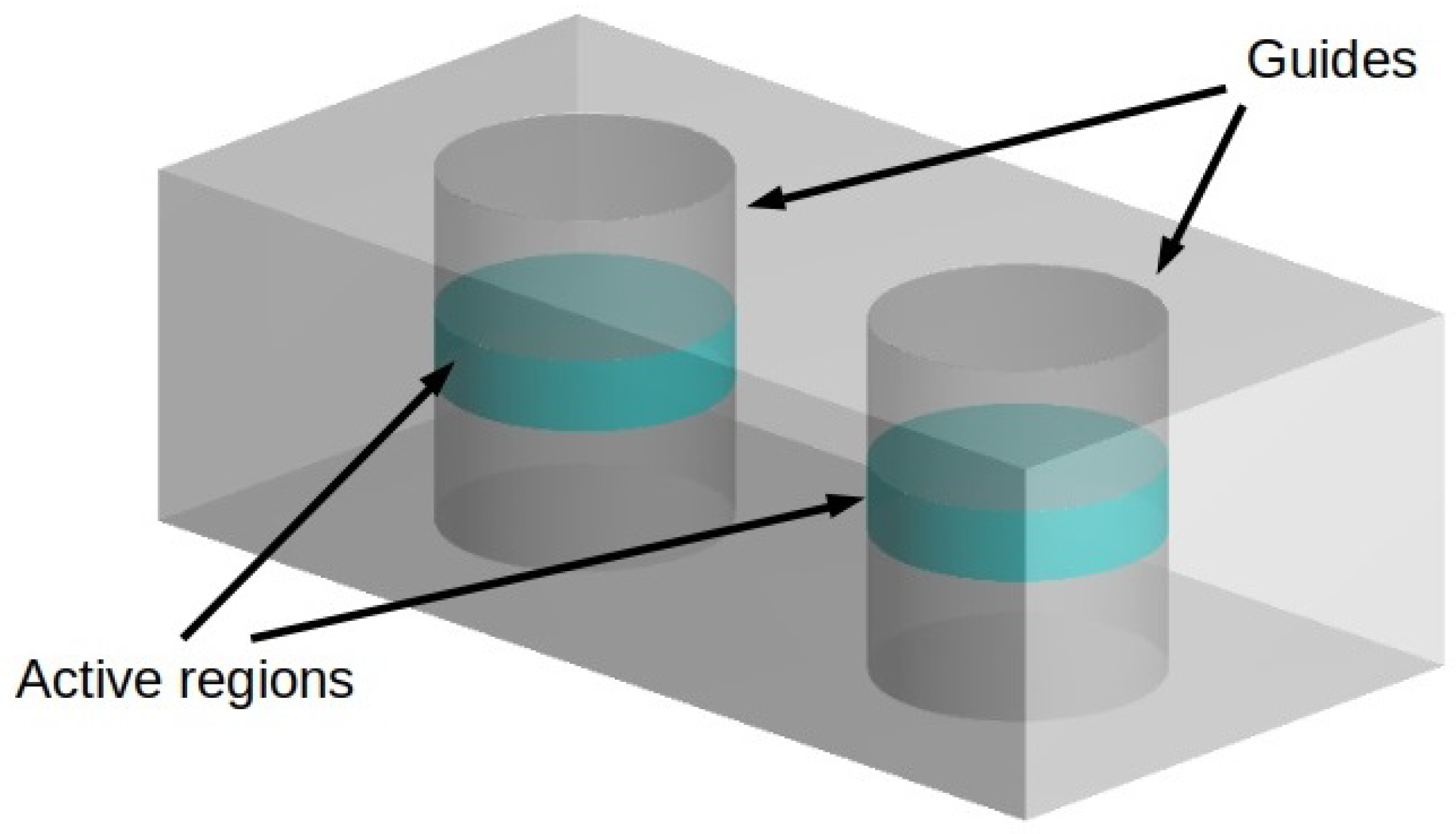
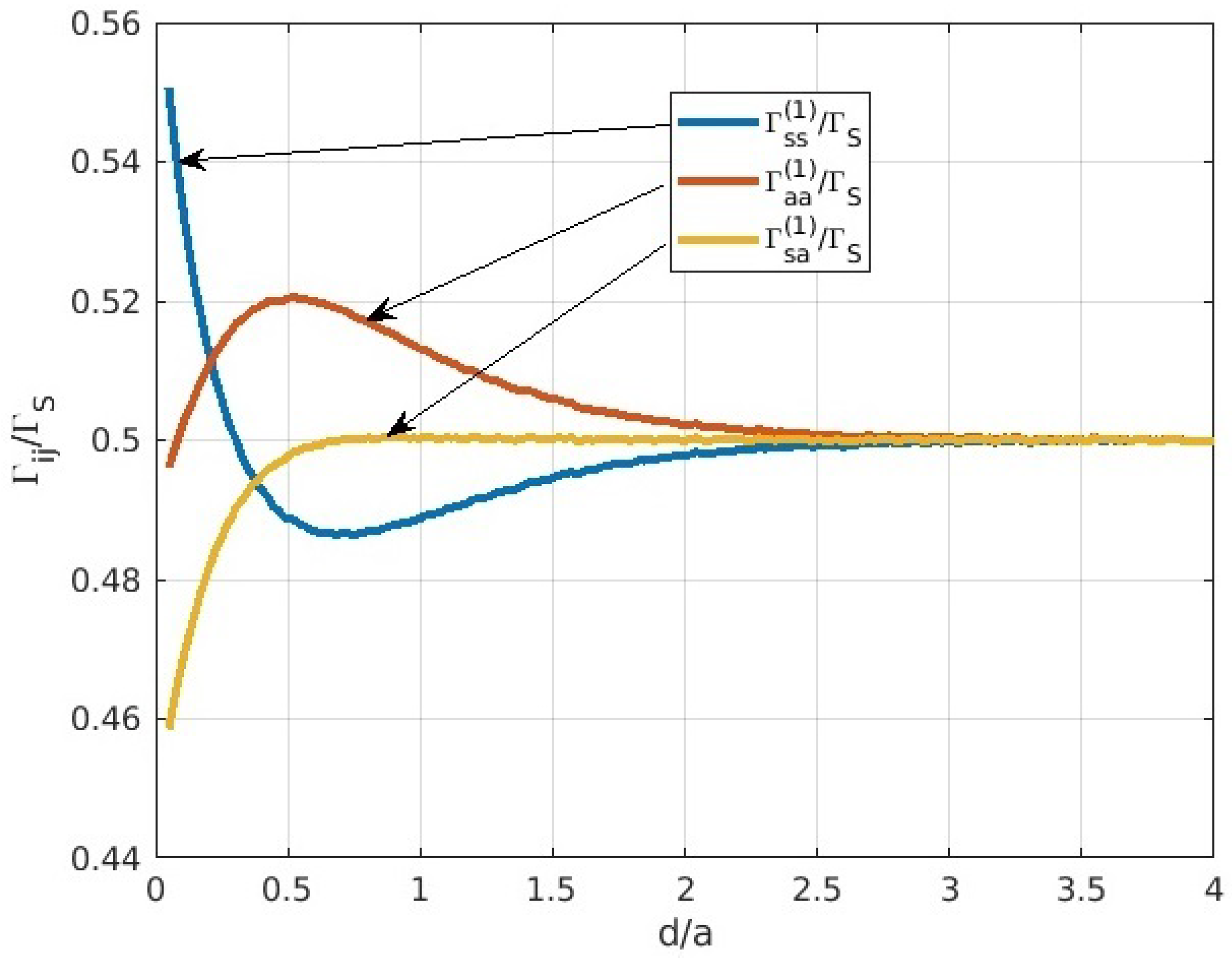
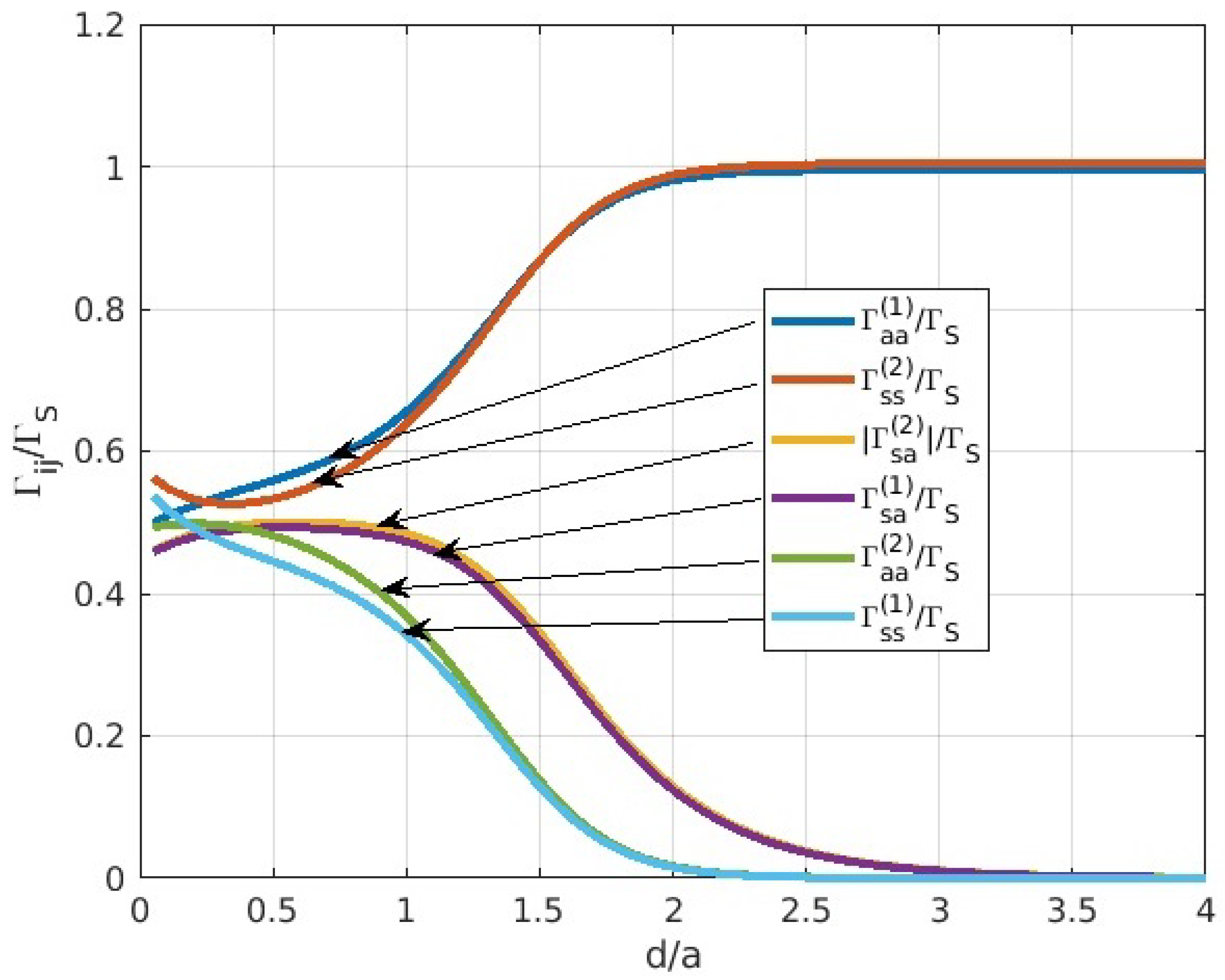
3. The Overlap Factors
3.1. Equal Guides
3.2. Unequal Guides
3.3. Circular Guides
4. Double-Guided Structure
4.1. Real Form of the Rate Equations
4.1.1. Optical Rate Equations
4.1.2. Carrier Rate Equations
4.1.3. Normalised Rate Equations
4.2. Limiting Behaviour for Widely Separated Guides
4.2.1. Reduction to the Spin-Flip Model (SFM)
4.2.2. Reduction to the Coupled Mode Model (CMM)
5. Steady State Solutions
5.1. Effect of Spin Relaxation
5.2. Equal Pumping
6. Results and Discussion
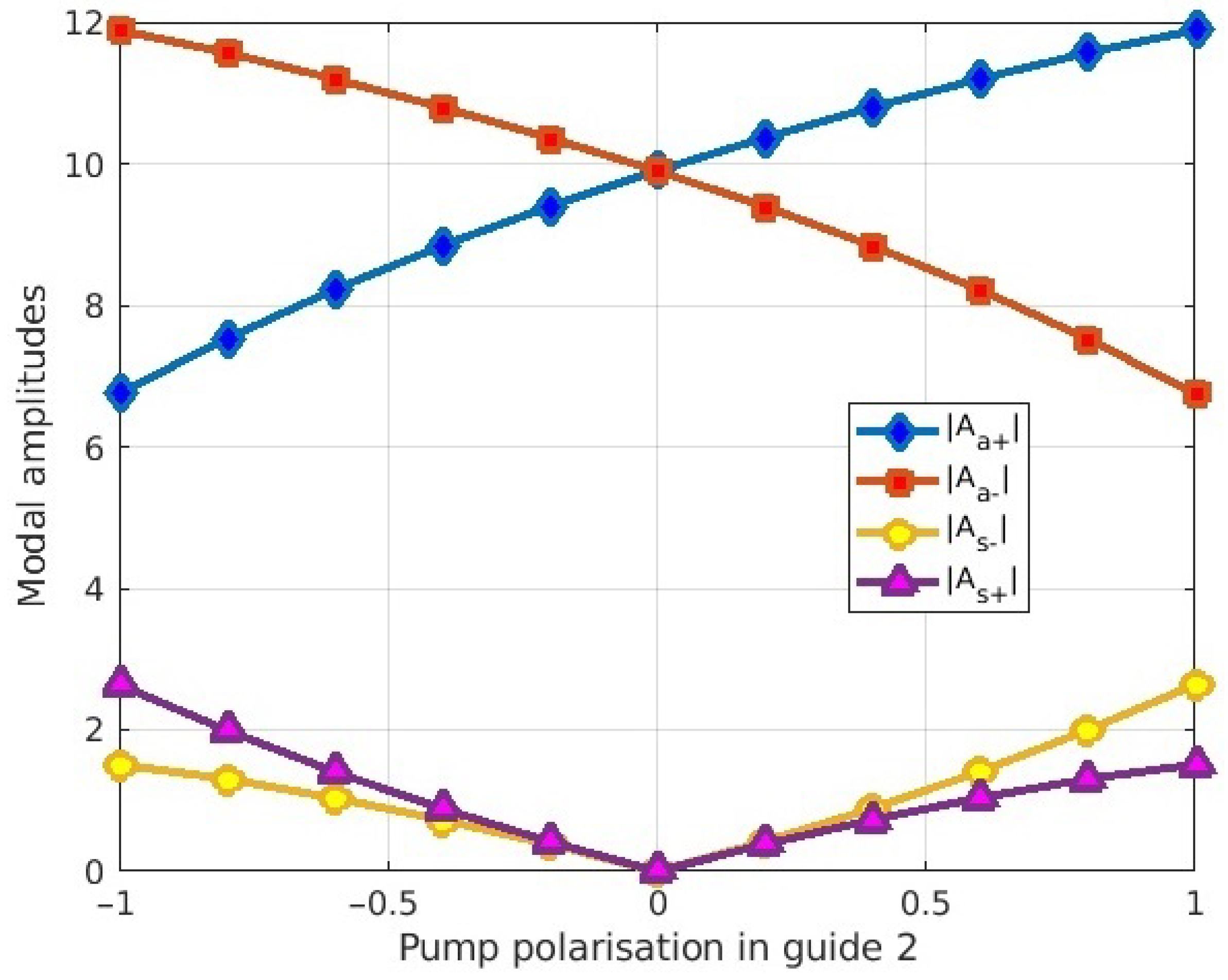
6.1. Numerical Solutions of the Rate Equations
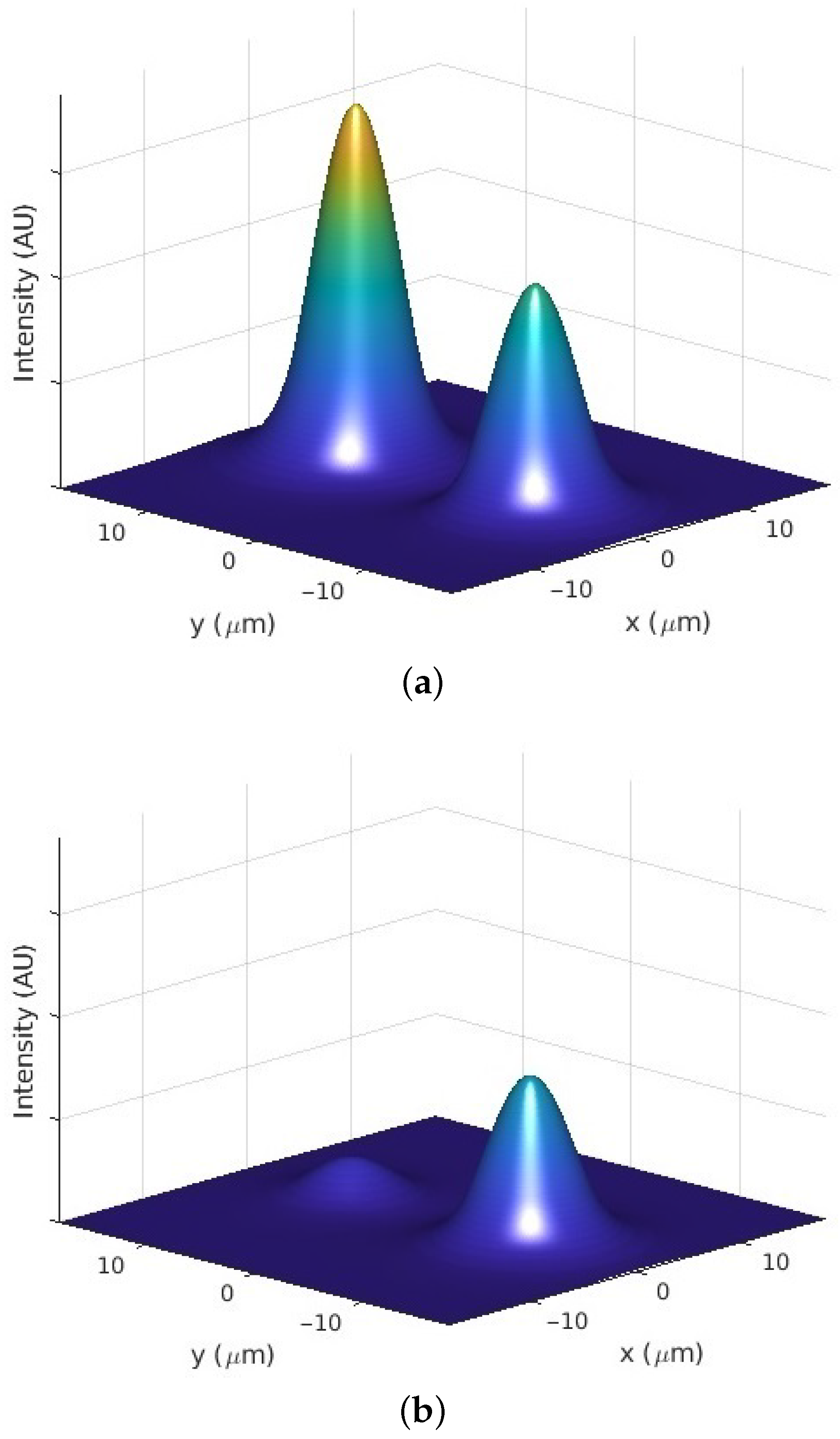
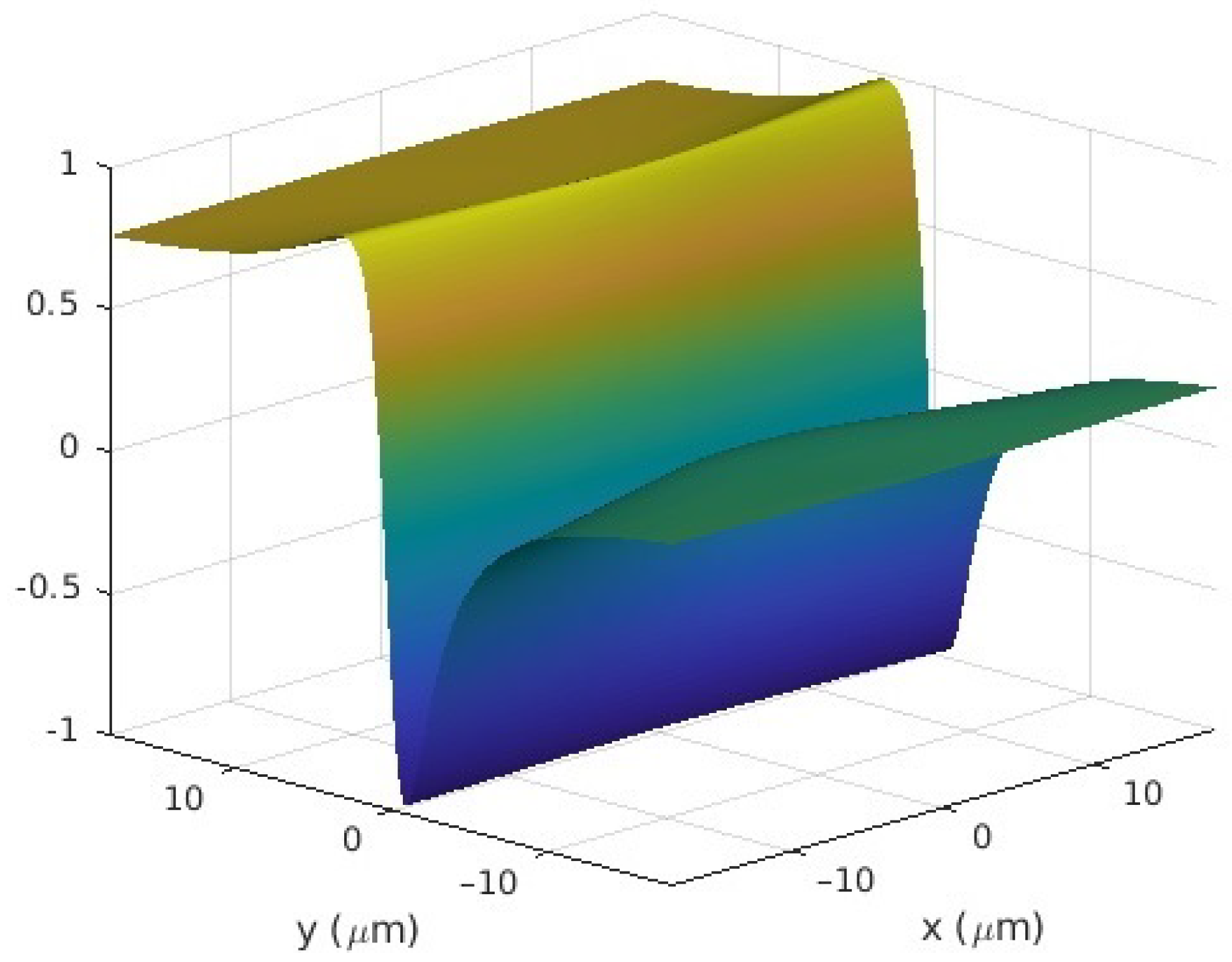
6.2. Spatial Profiles
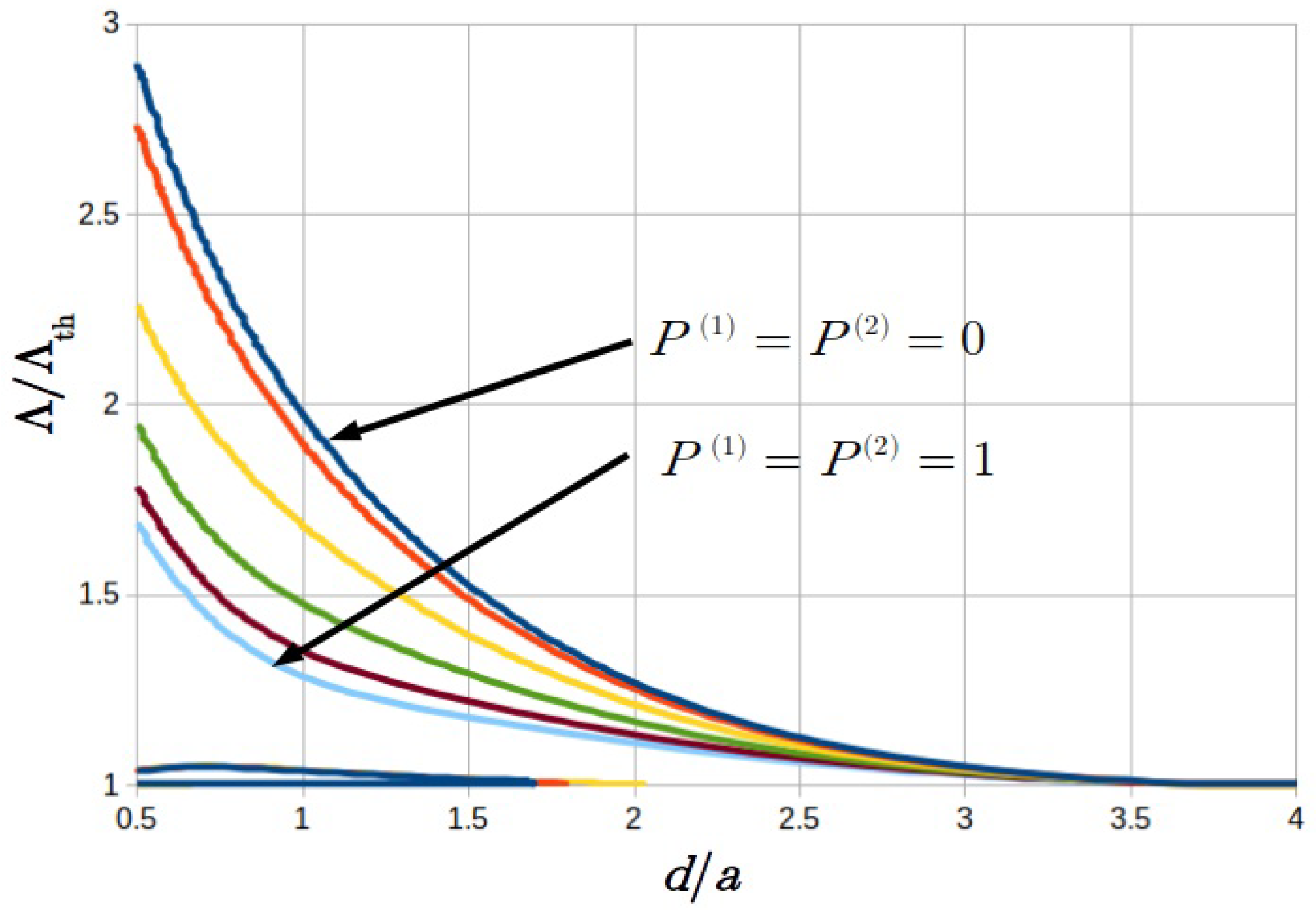
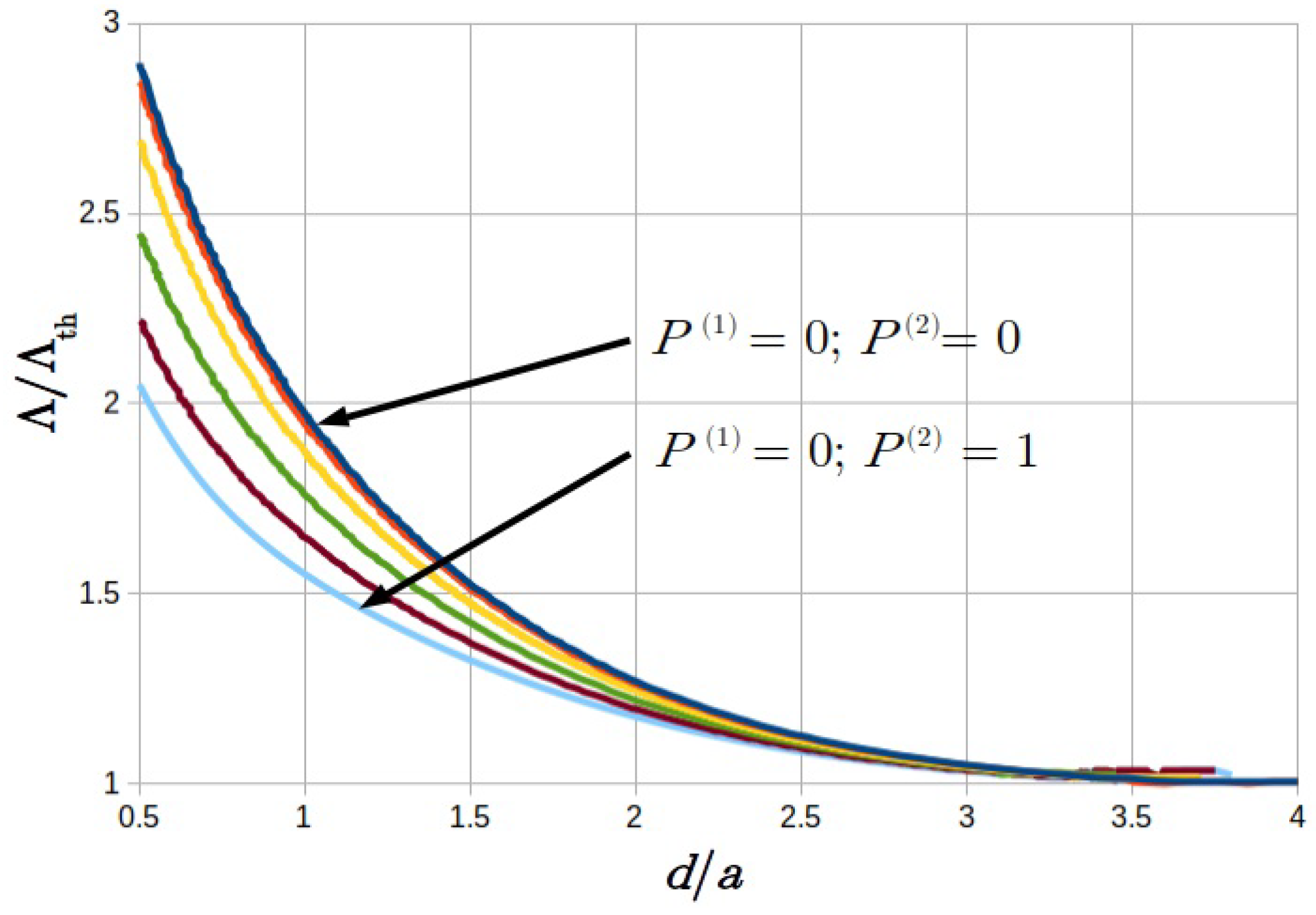
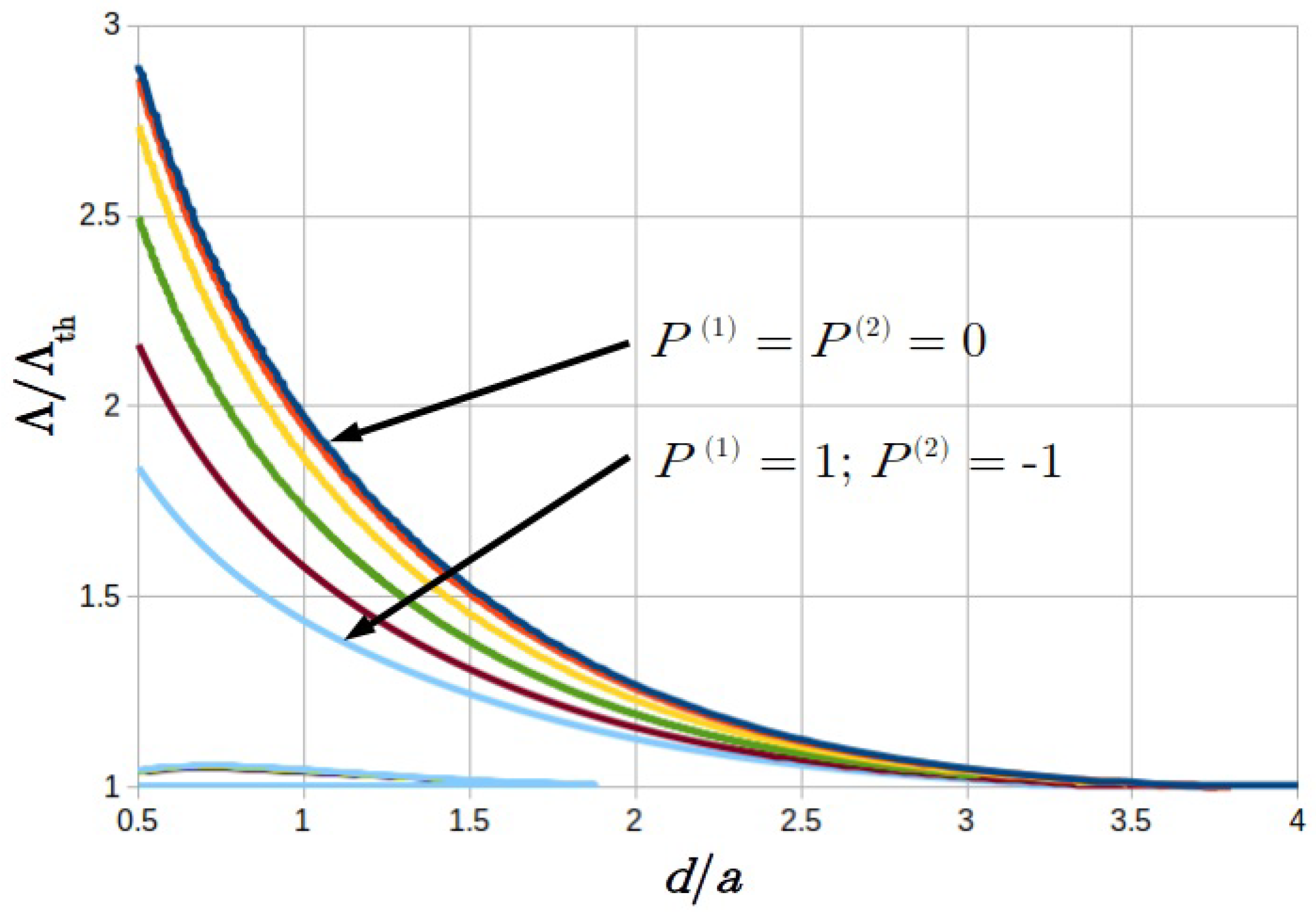
6.3. Stability Boundaries
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CMM | Coupled mode model |
| PS | Polarisation switching |
| SFM | Spin flip model |
| SVEA | Slowly varying envelope approximation |
| VCSEL | Vertical cavity surface emitting laser |
References
- Guo, X.X.; Xiang, S.Y.; Zhang, Y.H.; Lin, L.; Wen, A.J.; Hao, Y. Four-channels reservoir computing based on polarization dynamics in mutually coupled VCSELs system. Opt. Express 2019, 27, 23293–23306. [Google Scholar] [CrossRef]
- Jiang, N.; Xue, C.; Liu, D.; Lv, Y.; Qiu, K. Secure key distribution based on chaos synchronization of VCSELs subject to symmetric random-polarization optical injection. Opt. Lett. 2017, 42, 1055–1058. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Guo, X.X.; Xiang, S.Y. Key distribution based on unidirectional injection of vertical cavity surface emitting laser system. Acta Phys. Sin. 2018, 67, 204202. [Google Scholar]
- Jayaprasath, E.; Hou, Y.S.; Wu, Z.M.; Xia, G.Q. Anticipation in the Polarization Chaos Synchronization of Uni-Directionally Coupled Vertical-Cavity Surface-Emitting Lasers With Polarization-Preserved Optical Injection. IEEE Access 2018, 6, 58482–58490. [Google Scholar] [CrossRef]
- San Miguel, M.; Feng, Q.; Moloney, J.V. Light-polarization dynamics in surface-emitting semiconductor lasers. Phys. Rev. A 1995, 52, 1728–1739. [Google Scholar] [CrossRef] [PubMed]
- Erzgräber, H.; Wieczorek, S.; Krauskopf, B. Dynamics of two laterally coupled semiconductor lasers: Strong-and weak-coupling theory. Phys. Rev. E 2008, 78, 066201. [Google Scholar] [CrossRef]
- Martin-Regalado, J.; Prati, F.; San Miguel, M.; Abraham, N. Polarization properties of vertical-cavity surface-emitting lasers. IEEE J. Quantum Electron. 1997, 33, 765–783. [Google Scholar] [CrossRef]
- Travagnin, M.; van Exter, M.; Van Doorn, A.J.; Woerdman, J. Role of optical anisotropies in the polarization properties of surface-emitting semiconductor lasers. Phys. Rev. A 1996, 54, 1647–1660, Erratum in 1997, 55, 4641. [Google Scholar] [CrossRef]
- Balle, S.; Tolkachova, E.; San Miguel, M.; Tredicce, J.R.; Martin-Regalado, J.; Gahl, A. Mechanisms of polarization switching in single-transverse-mode vertical-cavity surface-emitting lasers: Thermal shift and nonlinear semiconductor dynamics. Opt. Lett. 1999, 24, 1121–1123. [Google Scholar] [CrossRef]
- Sondermann, M.; Ackemann, T.; Balle, S.; Mulet, J.; Panajotov, K. Experimental and theoretical investigations on elliptically polarized dynamical transition states in the polarization switching of vertical-cavity surface-emitting lasers. Opt. Commun. 2004, 235, 421–434. [Google Scholar] [CrossRef]
- Panajotov, K.; Pratl, F. Polarization dynamics of VCSELs. In VCSELs: Fundamentals, Technology and Applications of Vertical-Cavity Surface-Emitting Lasers; Springer Series in Optical Sciences, Chapter 6; Michalzik, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 166. [Google Scholar]
- Mulet, J.; Balle, S. Spatio-temporal modeling of the optical properties of VCSELs in the presence of polarization effects. IEEE J. Quantum Electron. 2002, 38, 291–305. [Google Scholar] [CrossRef]
- Masoller, C.; Torre, M. Modeling thermal effects and polarization competition in vertical-cavity surface-emitting lasers. Opt. Express 2008, 16, 21282–21296. [Google Scholar] [CrossRef]
- Gerhardt, N.C.; Hofmann, M.R. Spin-controlled vertical-cavity surface-emitting lasers. Adv. Opt. Technol. 2012, 2012, 268949. [Google Scholar] [CrossRef]
- Gahl, A.; Balle, S.; Miguel, M.S. Polarization dynamics of optically pumped VCSELs. IEEE J. Quantum Electron. 1999, 35, 342–351. [Google Scholar] [CrossRef]
- Gerhardt, N.; Hovel, S.; Hofmann, M.; Yang, J.; Reuter, D.; Wieck, A. Enhancement of spin information with vertical cavity surface emitting lasers. Electron. Lett. 2006, 42, 88–89. [Google Scholar] [CrossRef]
- Adams, M.J.; Alexandropoulos, D. Parametric analysis of spin-polarized VCSELs. IEEE J. Quantum Electron. 2009, 45, 744–749. [Google Scholar] [CrossRef]
- Adams, M.; Li, N.; Cemlyn, B.; Susanto, H.; Henning, I. Algebraic expressions for the polarisation response of spin-VCSELs. Semicond. Sci. Technol. 2018, 33, 064002. [Google Scholar] [CrossRef]
- Li, M.; Jähme, H.; Soldat, H.; Gerhardt, N.; Hofmann, M.; Ackemann, T. Birefringence controlled room-temperature picosecond spin dynamics close to the threshold of vertical-cavity surface-emitting laser devices. Appl. Phys. Lett. 2010, 97, 191114. [Google Scholar] [CrossRef]
- Lindemann, M.; Pusch, T.; Michalzik, R.; Gerhardt, N.C.; Hofmann, M.R. Frequency tuning of polarization oscillations: Toward high-speed spin-lasers. Appl. Phys. Lett. 2016, 108, 042404. [Google Scholar] [CrossRef]
- Torre, M.S.; Susanto, H.; Li, N.; Schires, K.; Salvide, M.; Henning, I.; Adams, M.; Hurtado, A. High frequency continuous birefringence-induced oscillations in spin-polarized vertical-cavity surface-emitting lasers. Opt. Lett. 2017, 42, 1628–1631. [Google Scholar] [CrossRef]
- Hendriks, R.; Van Exter, M.; Woerdman, J.; Van der Poel, C. Phase coupling of two optically pumped vertical-cavity surface-emitting lasers. Appl. Phys. Lett. 1996, 69, 869–871. [Google Scholar] [CrossRef]
- Ebeling, K.J.; Michalzik, R.; Moench, H. Vertical-cavity surface-emitting laser technology applications with focus on sensors and three-dimensional imaging. Japan. J. Appl. Phys. 2018, 57, 08PA02. [Google Scholar] [CrossRef]
- Czyszanowski, T.; Sarzała, R.P.; Dems, M.; Walczak, J.; Wasiak, M.; Nakwaski, W.; Iakovlev, V.; Volet, N.; Kapon, E. Spatial-mode discrimination in guided and antiguided arrays of long-wavelength VCSELs. IEEE J. Select. Top. Quantum Electron. 2013, 19, 1702010. [Google Scholar] [CrossRef][Green Version]
- Blackbeard, N.; Wieczorek, S.; Erzgräber, H.; Dutta, P.S. From synchronisation to persistent optical turbulence in laser arrays. Phys. D 2014, 286, 43–58. [Google Scholar] [CrossRef]
- Vicente, R.; Mulet, J.; Mirasso, C.R.; Sciamanna, M. Bistable polarization switching in mutually coupled vertical-cavity surface-emitting lasers. Opt. Lett. 2006, 31, 996–998. [Google Scholar] [CrossRef] [PubMed]
- Vaughan, M.; Susanto, H.; Henning, I.; Adams, M. Dynamics of laterally-coupled pairs of spin-VCSELs. IEEE J. Quantum Electron. 2020, 56, 2400310. [Google Scholar] [CrossRef]
- Vaughan, M.; Susanto, H.; Li, N.; Henning, I.; Adams, M. Stability boundaries in laterally-coupled pairs of semiconductor lasers. Photonics 2019, 6, 74. [Google Scholar] [CrossRef]
- Adams, M.; Li, N.; Cemlyn, B.; Susanto, H.; Henning, I. Effects of detuning, gain-guiding, and index antiguiding on the dynamics of two laterally coupled semiconductor lasers. Phys. Rev. A 2017, 95, 053869. [Google Scholar] [CrossRef]
- Martin-Regalado, J.; Balle, S.; San Miguel, M.; Valle, A.; Pesquera, L. Polarization and transverse-mode selection in quantum-well vertical-cavity surface-emitting lasers: Index-and gain-guided devices. Quantum Semiclass. Opt. 1997, 9, 713–736. [Google Scholar] [CrossRef]
- Vaughan, M.; Susanto, H.; Henning, I.; Adams, M. Analysis of evanescently-coupled pairs of spin-polarised vertical-cavity surface-emitting lasers. arXiv 2019, arXiv:1912.06882. [Google Scholar]
- Ogawa, K. Simplified theory of the multimode fiber coupler. Bell Syst. Tech. J. 1977, 56, 729–745. [Google Scholar] [CrossRef]
- Marom, E.; Ramer, O.; Ruschin, S. Relation between normal-mode and coupled-mode analyses of parallel waveguides. IEEE J. Quantum Electron. 1984, 20, 1311–1319. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math 1980, 6, 19–26. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The Matlab ODE suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Powell, M.J. A FORTRAN subroutine for solving systems of nonlinear algebraic equations. In Numerical Methods for Nonlinear Algebraic Equations; Rabinowitz, P., Ed.; Harwood Academic: Reading, UK, 1970. [Google Scholar]
- Coleman, T.F.; Li, Y. An interior trust region approach for nonlinear minimization subject to bounds. SIAM J. Optimiz. 1996, 6, 418–445. [Google Scholar] [CrossRef]
- Coleman, T.F.; Li, Y. On the convergence of interior-reflective Newton methods for nonlinear minimization subject to bounds. Math. Program. 1994, 67, 189–224. [Google Scholar] [CrossRef]



| Parameter | Value | Unit | Description |
|---|---|---|---|
| 3.400971 | - | Core refractive index | |
| 3.4 | - | Cladding refractive index | |
| a | 4 | Half guide width/radius | |
| 1.3 | Free-space wavelength |
| Parameter | Unit | |
|---|---|---|
| 0.200 | ||
| 0.399 | ||
| 0.247 | ||
| 0.441 | ||
| 0.5766 | - | |
| 0.346 | - | |
| 0.300 | - | |
| 0.3156 | - |
| Parameter | Value | Unit | Description |
|---|---|---|---|
| −2 | Linewidth enhancement | ||
| 70 | Cavity loss rate | ||
| 1 | Carrier loss rate | ||
| 0.1 | Dichroism rate | ||
| 2 | Birefringence rate | ||
| 100 | Effective spin relaxation rate | ||
| Transparency density | |||
| Differential gain | |||
| 3.4 | Group refractive index |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaughan, M.; Susanto, H.; Henning, I.; Adams, M. The Overlap Factor Model of Spin-Polarised Coupled Lasers. Photonics 2021, 8, 83. https://doi.org/10.3390/photonics8030083
Vaughan M, Susanto H, Henning I, Adams M. The Overlap Factor Model of Spin-Polarised Coupled Lasers. Photonics. 2021; 8(3):83. https://doi.org/10.3390/photonics8030083
Chicago/Turabian StyleVaughan, Martin, Hadi Susanto, Ian Henning, and Mike Adams. 2021. "The Overlap Factor Model of Spin-Polarised Coupled Lasers" Photonics 8, no. 3: 83. https://doi.org/10.3390/photonics8030083
APA StyleVaughan, M., Susanto, H., Henning, I., & Adams, M. (2021). The Overlap Factor Model of Spin-Polarised Coupled Lasers. Photonics, 8(3), 83. https://doi.org/10.3390/photonics8030083






