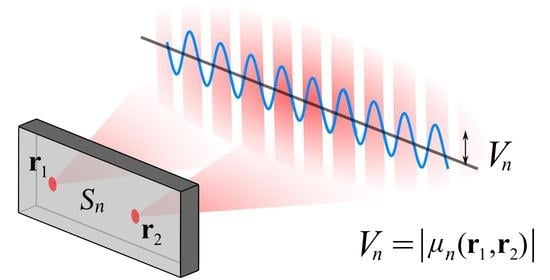
Coherence Stokes Parameters in the Description of Electromagnetic Coherence
Abstract
:1. Introduction
2. Definition of the Coherence Stokes Parameters
3. Intensity and Polarization Modulations in Young’s Two-Pinhole Interference
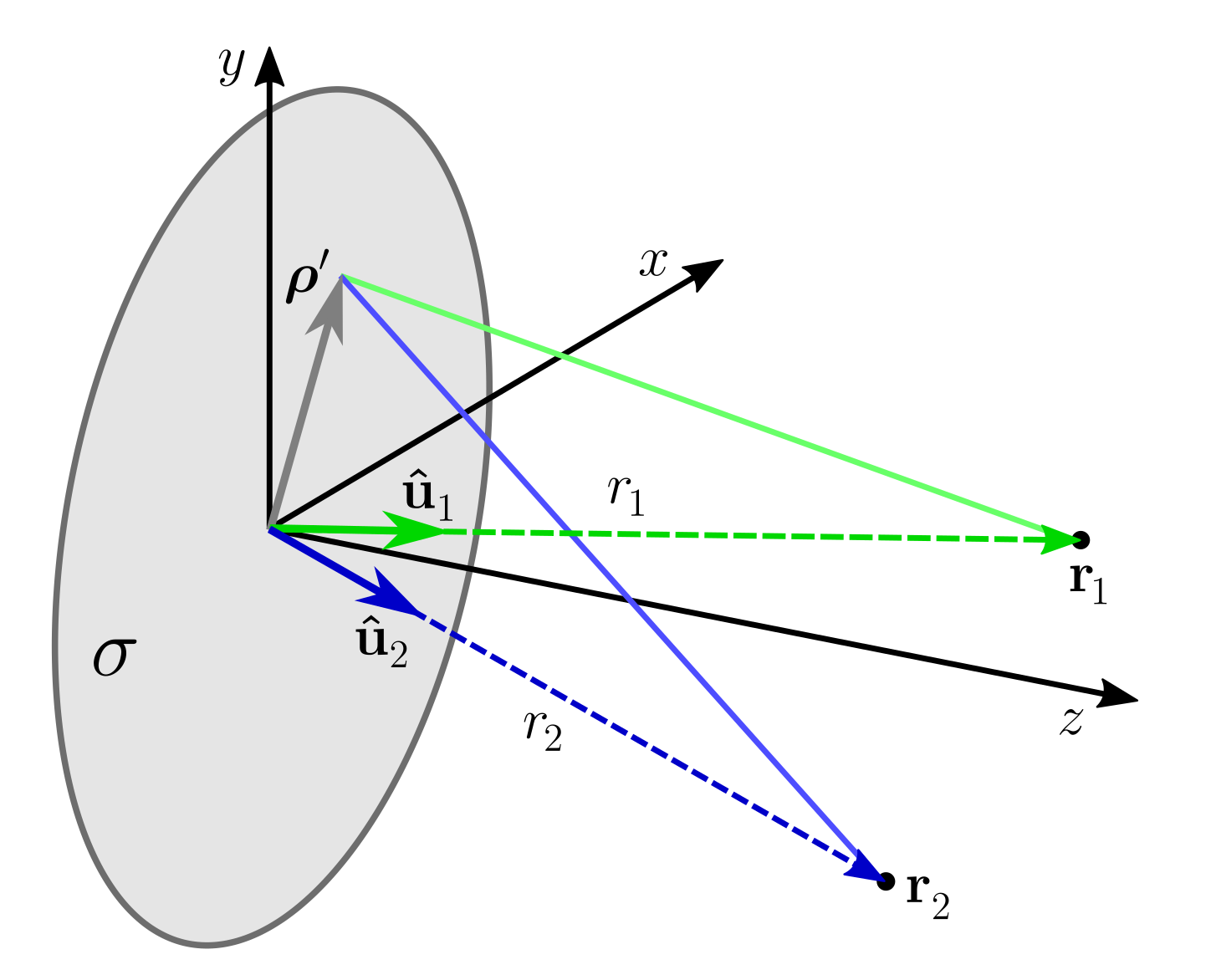
4. Far-Zone Form of the Van Cittert–Zernike Theorem with Stokes Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novotny, L.; Hecht, B. Principles of Nano-Optics, 2nd ed.; Cambridge University: Cambridge, UK, 2012. [Google Scholar]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University: Cambridge, UK, 1995. [Google Scholar]
- Korotkova, O. Random Light Beams: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Gil, J.J.; Ossikovski, R. Polarized Light and the Mueller Matrix Approach; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Friberg, A.T.; Setälä, T. Electromagnetic theory of optical coherence [Invited]. J. Opt. Soc. Am. A 2016, 33, 2431–2442. [Google Scholar] [CrossRef]
- Ellis, J.; Dogariu, A. Complex degree of mutual polarization. Opt. Lett. 2004, 29, 536–538. [Google Scholar] [CrossRef]
- Korotkova, O.; Wolf, E. Generalized Stokes parameters of random electromagnetic beams. Opt. Lett. 2005, 30, 198–200. [Google Scholar] [CrossRef]
- Tervo, J.; Setälä, T.; Roueff, A.; Réfrégier, P.; Friberg, A.T. Two-point Stokes parameters: Interpretation and properties. Opt. Lett. 2009, 34, 3074–3076. [Google Scholar] [CrossRef]
- Setälä, T.; Tervo, J.; Friberg, A.T. Stokes parameters and polarization contrasts in Young’s interference experiment. Opt. Lett. 2006, 31, 2208–2210. [Google Scholar] [CrossRef]
- Setälä, T.; Tervo, J.; Friberg, A.T. Contrasts of Stokes parameters in Young’s interference experiment and electromagnetic degree of coherence. Opt. Lett. 2006, 31, 2669–2671. [Google Scholar] [CrossRef] [PubMed]
- Kanseri, B.; Kandpal, H.C. Experimental determination of electric cross-spectral density matrix and generalized Stokes parameters for a laser beam. Opt. Lett. 2008, 33, 2410–2412. [Google Scholar] [CrossRef] [Green Version]
- Kanseri, B.; Rath, S.; Kandpal, H.C. Direct determination of the generalized Stokes parameters from the usual Stokes parameters. Opt. Lett. 2009, 34, 719–721. [Google Scholar] [CrossRef] [Green Version]
- Leppänen, L.-P.; Saastamoinen, K.; Friberg, A.T.; Setälä, T. Interferometric interpretation for the degree of polarization of classical optical beams. New J. Phys. 2014, 16, 113059. [Google Scholar] [CrossRef]
- Leppänen, L.-P.; Friberg, A.T.; Setälä, T. Temporal electromagnetic degree of coherence and the Stokes-parameter modulations in Michelson’s interferometer. Appl. Phys. B 2016, 122, 32. [Google Scholar] [CrossRef]
- Leppänen, L.-P.; Saastamoinen, K.; Friberg, A.T.; Setälä, T. Measurement of the degree of temporal coherence of unpolarized light beams. Photonics Res. 2017, 5, 156–161. [Google Scholar] [CrossRef] [Green Version]
- Tervo, J.; Setälä, T.; Turunen, J.; Friberg, A.T. Van Cittert–Zernike theorem with Stokes parameters. Opt. Lett. 2013, 38, 2301–2303. [Google Scholar] [CrossRef]
- Leppänen, L.-P.; Saastamoinen, K.; Friberg, A.T.; Setälä, T. Detection of electromagnetic degree of coherence with nanoscatterers: Comparison with Young’s interferometer. Opt. Lett. 2015, 40, 2898–2900. [Google Scholar] [CrossRef]
- Saastamoinen, K.; Partanen, H.; Friberg, A.T.; Setälä, T. Probing the electromagnetic degree of coherence of light beams with nanoscatterers. ACS Photonics 2020, 7, 1030–1035. [Google Scholar] [CrossRef]
- Norrman, A.; Friberg, A.T.; Leuchs, G. Vector-light quantum complementarity and the degree of polarization. Optica 2020, 7, 93–97. [Google Scholar] [CrossRef]
- Jacobson, A.D. An analysis of the second moment of fluctuating electromagnetic fields part I: Theory. IEEE Trans. Antennas Propag. 1967, 15, 24–32. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M.; Borghi, R.; Piquero, G. Use of the van Cittert–Zernike theorem for partially polarized sources. Opt. Lett. 2000, 25, 1291–1293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alonso, M.A.; Korotkova, O.; Wolf, E. Propagation of the electric correlation matrix and the van Cittert–Zernike theorem for random electromagnetic fields. J. Mod. Opt. 2006, 53, 969–978. [Google Scholar] [CrossRef]
- Ostrovsky, A.S.; Martínez-Niconoff, G.; Martínez-Vara, P.; Olvera-Santamaría, M.A. The van Cittert–Zernike theorem for electromagnetic fields. Opt. Express 2009, 17, 1746–1752. [Google Scholar] [CrossRef]
- Shirai, T. Some consequences of the van Cittert–Zernike theorem for partially polarized stochastic electromagnetic fields. Opt. Lett. 2009, 34, 3761–3763. [Google Scholar] [CrossRef]
- Rodríguez-Herrera, O.G.; Tyo, J.S. Generalized van Cittert–Zernike theorem for the cross-spectral density matrix of quasi-homogeneous planar electromagnetic sources. J. Opt. Soc. Am. A 2012, 29, 1939–1947. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setälä, T.; Saastamoinen, K.; Friberg, A.T. Coherence Stokes Parameters in the Description of Electromagnetic Coherence. Photonics 2021, 8, 85. https://doi.org/10.3390/photonics8030085
Setälä T, Saastamoinen K, Friberg AT. Coherence Stokes Parameters in the Description of Electromagnetic Coherence. Photonics. 2021; 8(3):85. https://doi.org/10.3390/photonics8030085
Chicago/Turabian StyleSetälä, Tero, Kimmo Saastamoinen, and Ari T. Friberg. 2021. "Coherence Stokes Parameters in the Description of Electromagnetic Coherence" Photonics 8, no. 3: 85. https://doi.org/10.3390/photonics8030085
APA StyleSetälä, T., Saastamoinen, K., & Friberg, A. T. (2021). Coherence Stokes Parameters in the Description of Electromagnetic Coherence. Photonics, 8(3), 85. https://doi.org/10.3390/photonics8030085