Compressional Optical Coherence Elastography of the Cornea
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cornea Samples
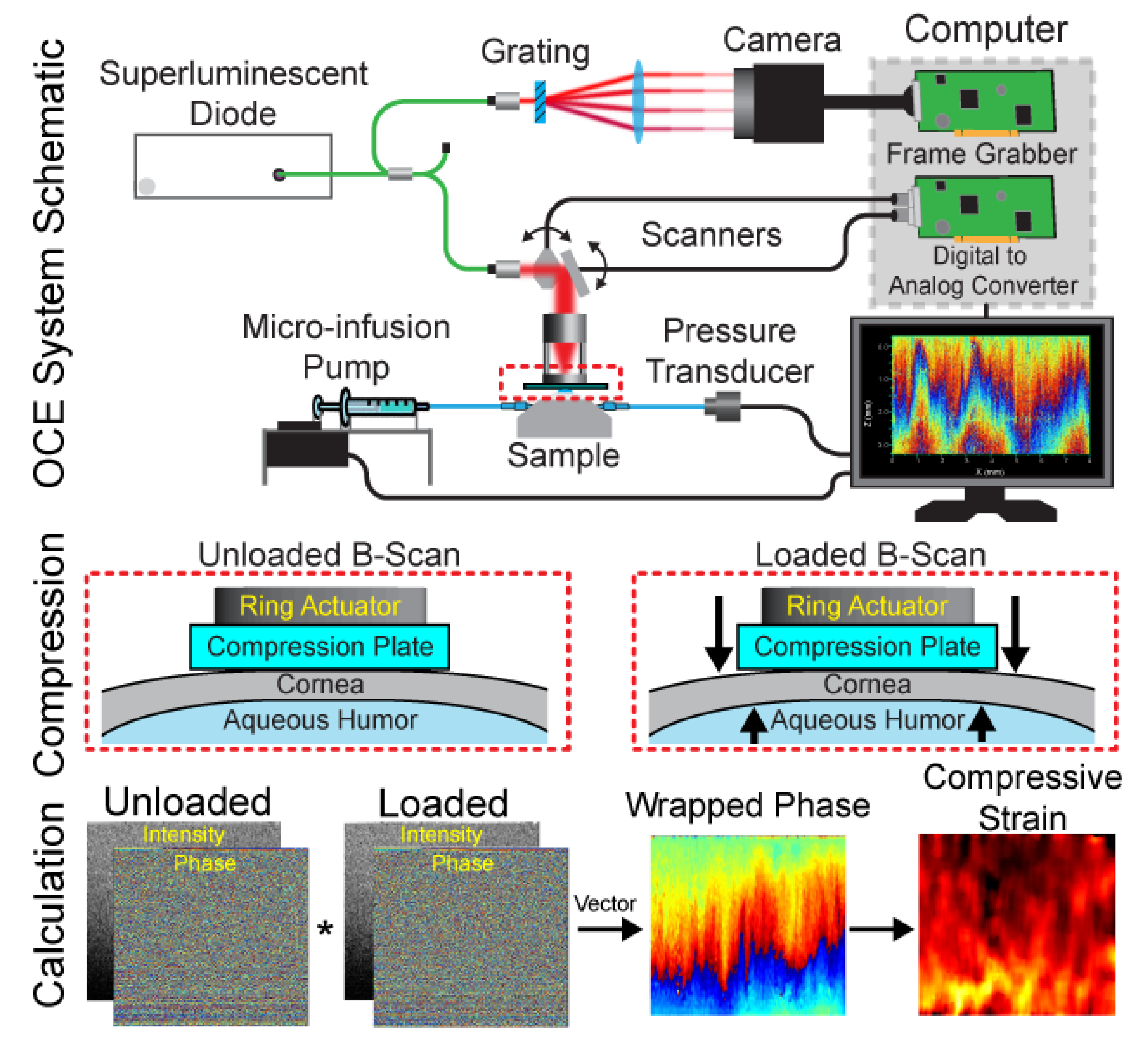
2.2. OCE Imaging
2.3. Statistical Analyses
3. Results
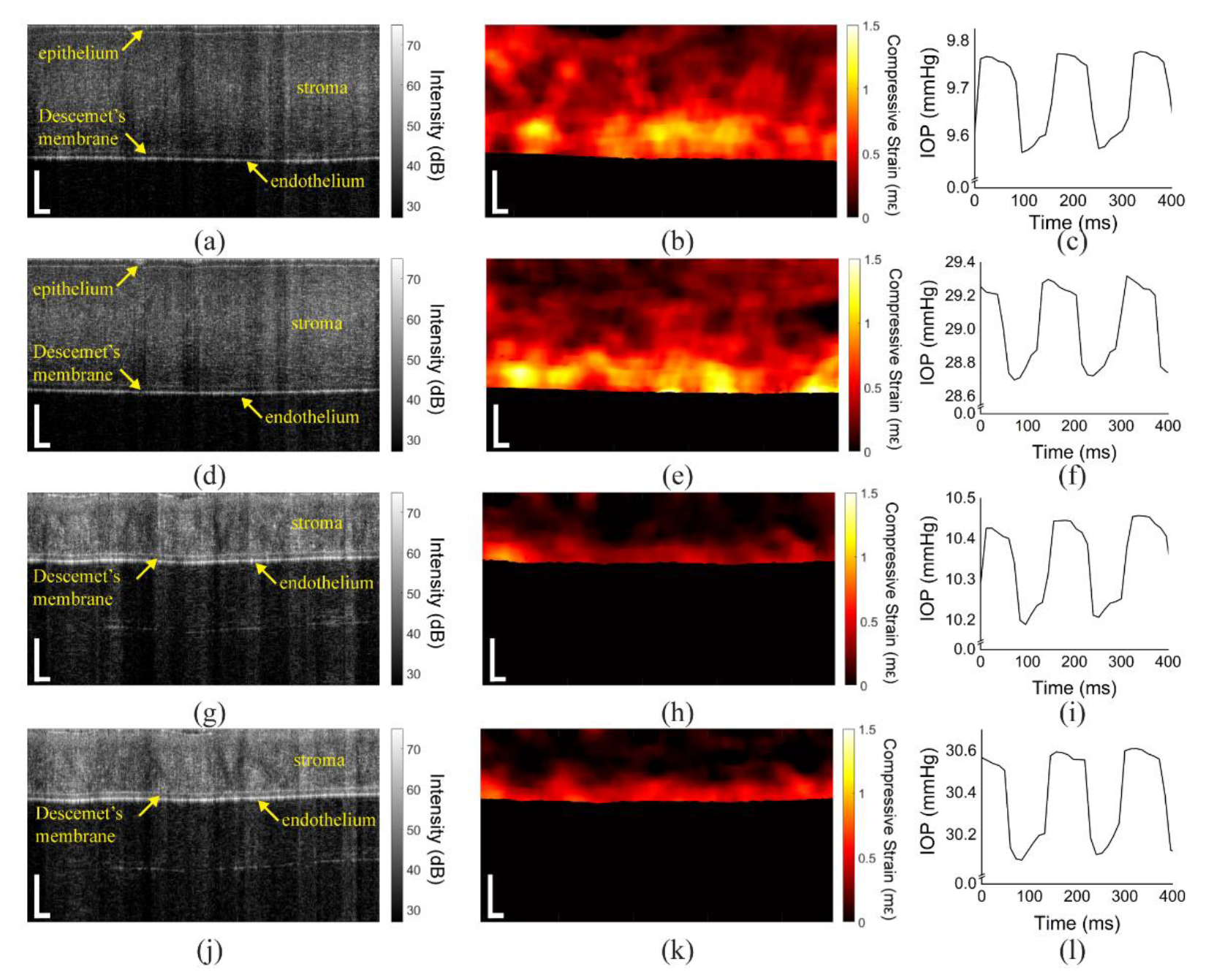
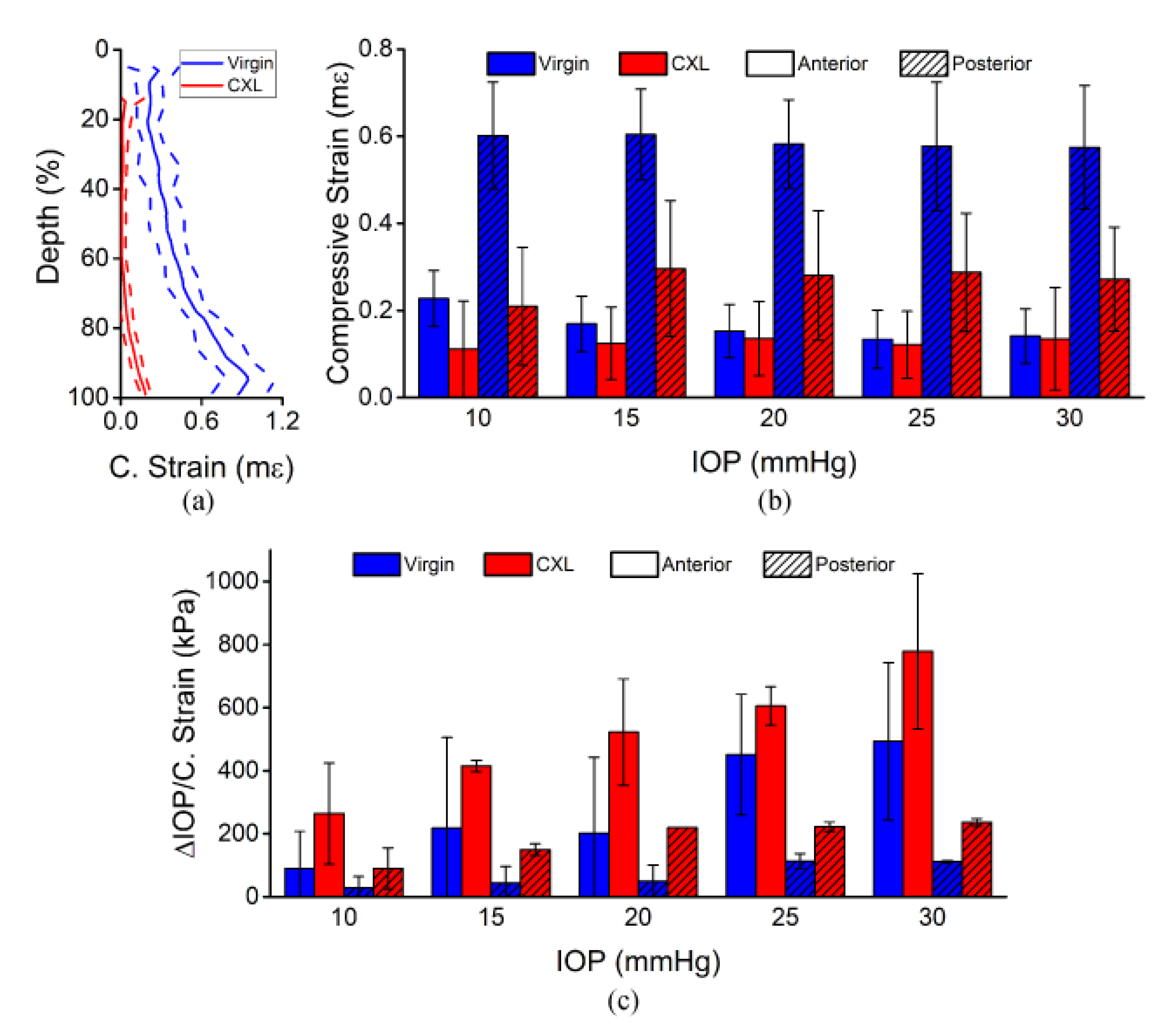
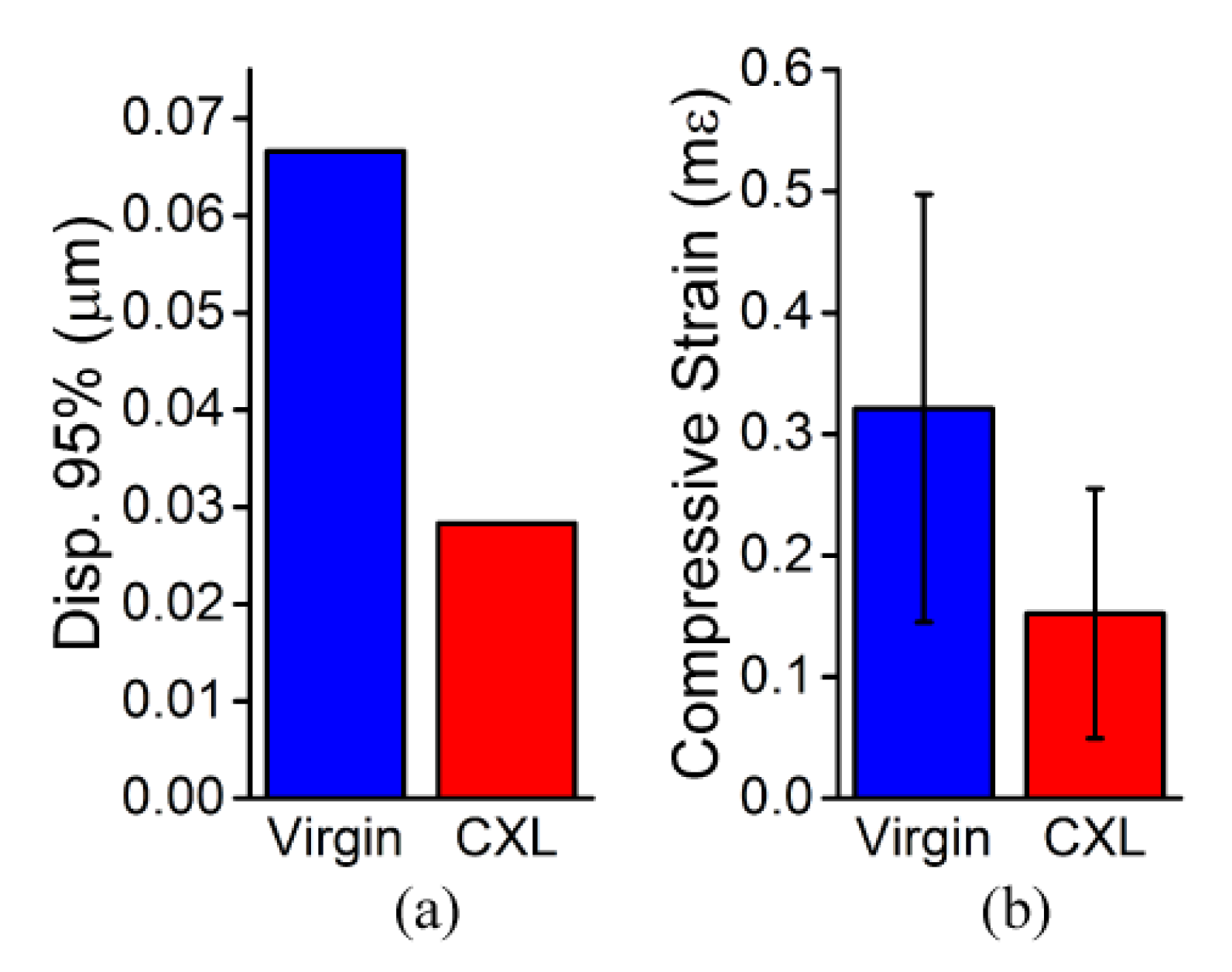
3.1. In Situ Rabbit Corneas
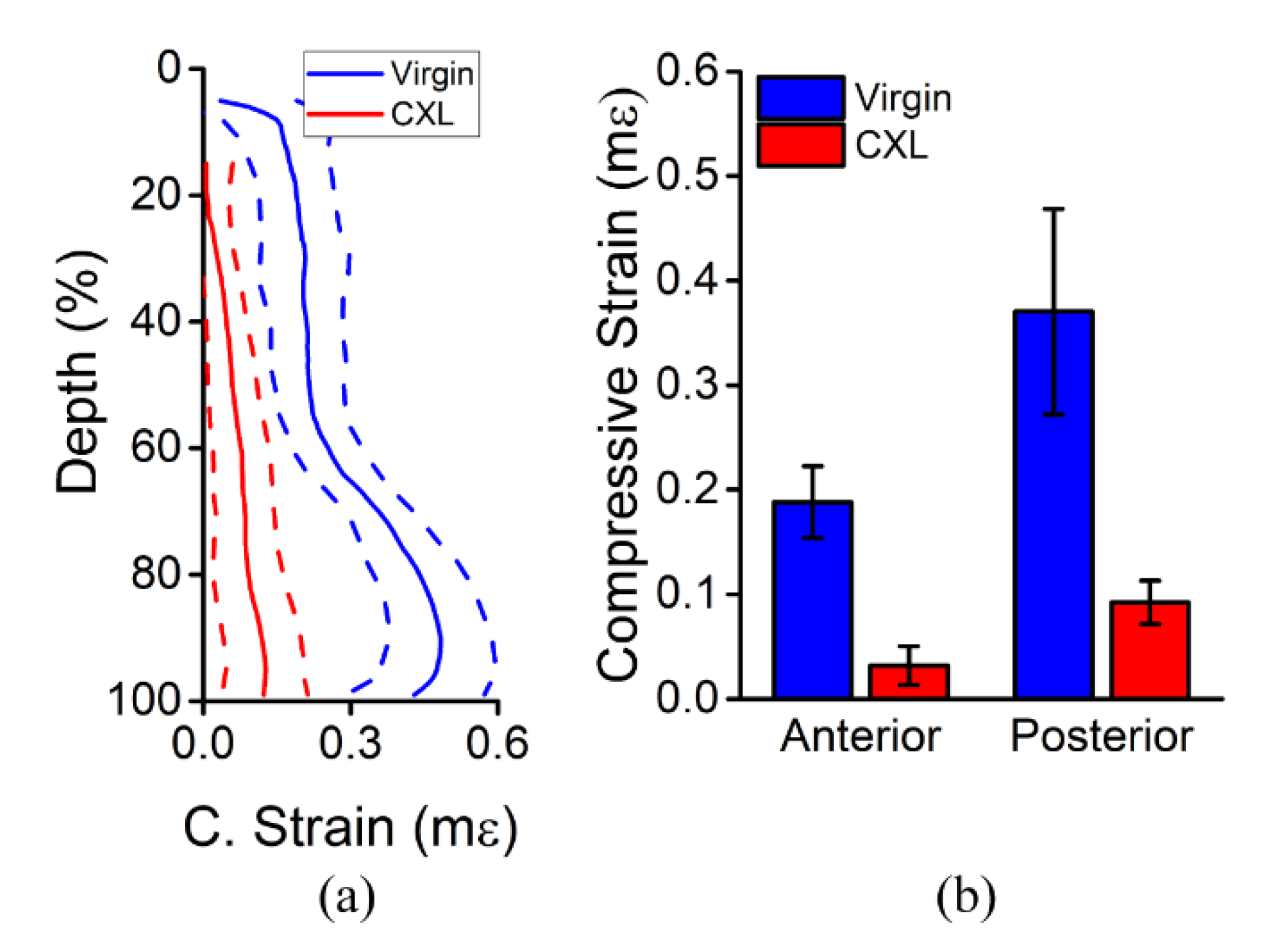
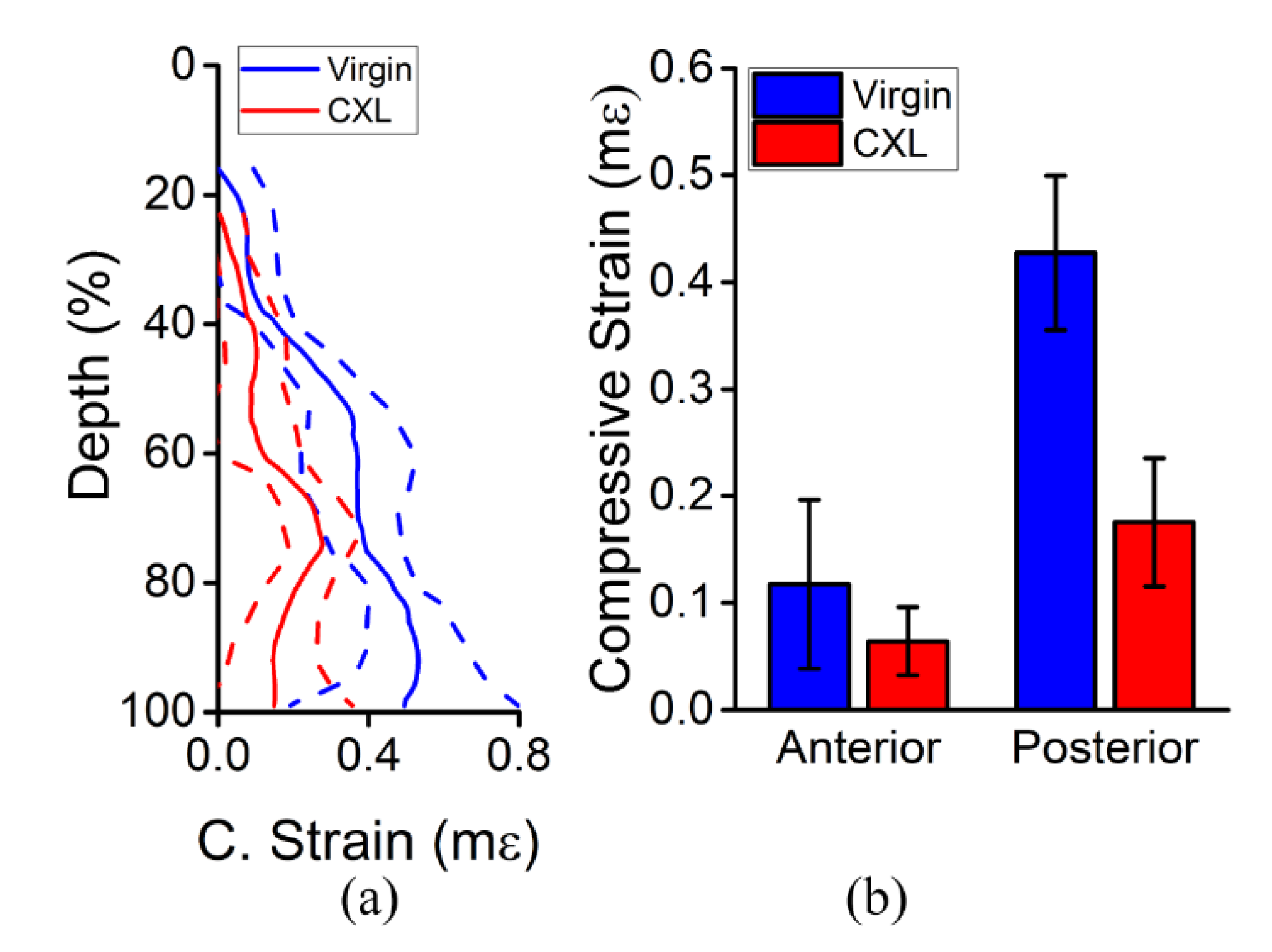
3.2. In Vivo Rabbit Corneas
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ruberti, J.W.; Sinha Roy, A.; Roberts, C.J. Corneal biomechanics and biomaterials. Annu. Rev. Biomed. Eng. 2011, 13, 269–295. [Google Scholar] [CrossRef]
- Alió, J.L. Keratoconus: Recent Advances in Diagnosis and Treatment; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Guo, H.; Hosseini-Moghaddam, S.M.; Hodge, W. Corneal biomechanical properties after smile versus flex, lasik, lasek, or prk: A systematic review and meta-analysis. BMC Ophthalmol. 2019, 19, 167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Litwiller, D.V.; Lee, S.J.; Kolipaka, A.; Mariappan, Y.K.; Glaser, K.J.; Pulido, J.S.; Ehman, R.L. Mr elastography of the ex vivo bovine globe. J. Magn. Reson. Imaging 2010, 32, 44–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osapoetra, L.O.; Watson, D.M.; McAleavey, S.A. Intraocular pressure-dependent corneal elasticity measurement using high-frequency ultrasound. Ultrason. Imaging 2019, 41, 251–270. [Google Scholar] [CrossRef] [PubMed]
- Tanter, M.; Touboul, D.; Gennisson, J.L.; Bercoff, J.; Fink, M. High-resolution quantitative imaging of cornea elasticity using supersonic shear imaging. IEEE Trans. Med. Imaging 2009, 28, 1881–1893. [Google Scholar] [CrossRef]
- Faruk, T.; Islam, M.K.; Arefin, S.; Haq, M.Z. The journey of elastography: Background, current status, and future possibilities in breast cancer diagnosis. Clin. Breast Cancer 2015, 15, 313–324. [Google Scholar] [CrossRef]
- Srinivasa Babu, A.; Wells, M.L.; Teytelboym, O.M.; Mackey, J.E.; Miller, F.H.; Yeh, B.M.; Ehman, R.L.; Venkatesh, S.K. Elastography in chronic liver disease: Modalities, techniques, limitations, and future directions. Radiographics 2016, 36, 1987–2006. [Google Scholar] [CrossRef]
- Bak-Nielsen, S.; Pedersen, I.B.; Ivarsen, A.; Hjortdal, J. Dynamic scheimpflug-based assessment of keratoconus and the effects of corneal cross-linking. J. Refract. Surg. 2014, 30, 408–414. [Google Scholar] [CrossRef]
- Gkika, M.; Labiris, G.; Giarmoukakis, A.; Koutsogianni, A.; Kozobolis, V. Evaluation of corneal hysteresis and corneal resistance factor after corneal cross-linking for keratoconus. Graefes Arch. Clin. Exp. Ophthalmol. 2012, 250, 565–573. [Google Scholar] [CrossRef] [PubMed]
- Greenstein, S.A.; Fry, K.L.; Hersh, P.S. In vivo biomechanical changes after corneal collagen cross-linking for keratoconus and corneal ectasia: 1-year analysis of a randomized, controlled, clinical trial. Cornea 2012, 31, 21–25. [Google Scholar] [CrossRef]
- Fontes, B.M.; Ambrosio, R., Jr.; Velarde, G.C.; Nose, W. Corneal biomechanical evaluation in healthy thin corneas compared with matched keratoconus cases. Arq. Bras. Oftalmol. 2011, 74, 13–16. [Google Scholar] [CrossRef] [Green Version]
- Wu, P.J.; Kabakova, I.V.; Ruberti, J.W.; Sherwood, J.M.; Dunlop, I.E.; Paterson, C.; Török, P.; Overby, D.R. Water content, not stiffness, dominates brillouin spectroscopy measurements in hydrated materials. Nat. Meth. 2018, 15, 561–562. [Google Scholar] [CrossRef] [PubMed]
- Shao, P.; Eltony, A.M.; Seiler, T.G.; Tavakol, B.; Pineda, R.; Koller, T.; Seiler, T.; Yun, S.H. Spatially-resolved brillouin spectroscopy reveals biomechanical abnormalities in mild to advanced keratoconus in vivo. Sci. Rep. 2019, 9, 7467. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A.; et al. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmitt, J. Oct elastography: Imaging microscopic deformation and strain of tissue. Opt. Express 1998, 3, 199–211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Larin, K.V.; Sampson, D.D. Optical coherence elastography—OCT at work in tissue biomechanics [invited]. Biomed. Opt. Express 2017, 8, 1172–1202. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, B.F.; Wijesinghe, P.; Sampson, D.D. The emergence of optical elastography in biomedicine. Nat. Photonics 2017, 11, 215–221. [Google Scholar] [CrossRef]
- Kennedy, B.F.; Kennedy, K.M.; Sampson, D.D. A review of optical coherence elastography: Fundamentals, techniques and prospects. IEEE J. Sel. Top. Quant. 2014, 20, 272–288. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Matveyev, A.L.; Matveev, L.A.; Sovetsky, A.A.; Hepburn, M.S.; Mowla, A.; Kennedy, B.F. Strain and elasticity imaging in compression optical coherence elastography: The two-decade perspective and recent advances. J. Biophotonics 2021, 14, e202000257. [Google Scholar] [CrossRef]
- Zvietcovich, F.; Pongchalee, P.; Meemon, P.; Rolland, J.P.; Parker, K.J. Reverberant 3d optical coherence elastography maps the elasticity of individual corneal layers. Nat. Commun. 2019, 10, 4895. [Google Scholar] [CrossRef] [Green Version]
- Ford, M.R.; Dupps, W.J., Jr.; Rollins, A.M.; Sinha, R.A.; Hu, Z. Method for optical coherence elastography of the cornea. J. Biomed. Opt. 2011, 16, 016005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Stefano, V.S.; Ford, M.R.; Seven, I.; Dupps, W.J., Jr. Live human assessment of depth-dependent corneal displacements with swept-source optical coherence elastography. PLoS ONE 2018, 13, e0209480. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ford, M.R.; Sinha Roy, A.; Rollins, A.M.; Dupps, W.J., Jr. Serial biomechanical comparison of edematous, normal, and collagen crosslinked human donor corneas using optical coherence elastography. J. Cataract Refract. Surg. 2014, 40, 1041–1047. [Google Scholar] [CrossRef] [Green Version]
- Torricelli, A.A.; Ford, M.R.; Singh, V.; Santhiago, M.R.; Dupps, W.J., Jr.; Wilson, S.E. Bac-edta transepithelial riboflavin-uva crosslinking has greater biomechanical stiffening effect than standard epithelium-off in rabbit corneas. Exp. Eye Res. 2014, 125, 114–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaitsev, V.Y.; Matveyev, A.L.; Matveev, L.A.; Gelikonov, G.V.; Omelchenko, A.I.; Baum, O.I.; Avetisov, S.E.; Bolshunov, A.V.; Siplivy, V.I.; Shabanov, D.V.; et al. Optical coherence elastography for strain dynamics measurements in laser correction of cornea shape. J. Biophotonics 2017, 10, 1450–1463. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Matveyev, A.L.; Matveev, L.A.; Gelikonov, G.V.; Baum, O.I.; Omelchenko, A.I.; Shabanov, D.V.; Sovetsky, A.A.; Yuzhakov, A.V.; Fedorov, A.A.; et al. Revealing structural modifications in thermomechanical reshaping of collagenous tissues using optical coherence elastography. J. Biophotonics 2019, 12, e201800250. [Google Scholar] [CrossRef] [PubMed]
- Twa, M.D.; Li, J.; Vantipalli, S.; Singh, M.; Aglyamov, S.; Emelianov, S.; Larin, K.V. Spatial characterization of corneal biomechanical properties with optical coherence elastography after uv cross-linking. Biomed. Opt. Express 2014, 5, 1419–1427. [Google Scholar] [CrossRef] [Green Version]
- Wollensak, G.; Spoerl, E.; Seiler, T. Riboflavin/ultraviolet-a-induced collagen crosslinking for the treatment of keratoconus. Am. J. Ophthalmol. 2003, 135, 620–627. [Google Scholar] [CrossRef]
- Nair, A.; Singh, M.; Aglyamov, S.R.; Larin, K.V. Heartbeat oce: Corneal biomechanical response to simulated heartbeat pulsation measured by optical coherence elastography. J. Biomed. Opt. 2020, 25, 1–9. [Google Scholar] [CrossRef]
- Vakhtin, A.B.; Kane, D.J.; Wood, W.R.; Peterson, K.A. Common-path interferometer for frequency-domain optical coherence tomography. Appl. Opt. 2003, 42, 6953–6958. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, B.F.; McLaughlin, R.A.; Kennedy, K.M.; Chin, L.; Curatolo, A.; Tien, A.; Latham, B.; Saunders, C.M.; Sampson, D.D. Optical coherence micro-elastography: Mechanical-contrast imaging of tissue microstructure. Biomed. Opt. Express 2014, 5, 2113–2124. [Google Scholar] [CrossRef] [Green Version]
- Lan, G.; Singh, M.; Larin, K.V.; Twa, M.D. Common-path phase-sensitive optical coherence tomography provides enhanced phase stability and detection sensitivity for dynamic elastography. Biomed. Opt. Express 2017, 8, 5253–5266. [Google Scholar] [CrossRef] [Green Version]
- Han, Z.; Li, J.; Singh, M.; Wu, C.; Liu, C.H.; Raghunathan, R.; Aglyamov, S.R.; Vantipalli, S.; Twa, M.D.; Larin, K.V. Optical coherence elastography assessment of corneal viscoelasticity with a modified rayleigh-lamb wave model. J. Mech. Behav. Biomed. Mater. 2017, 66, 87–94. [Google Scholar] [CrossRef] [Green Version]
- Matveyev, A.L.; Matveev, L.A.; Sovetsky, A.A.; Gelikonov, G.V.; Moiseev, A.A.; Zaitsev, V.Y. Vector method for strain estimation in phase-sensitive optical coherence elastography. Laser Phys. Lett. 2018, 15, 065603. [Google Scholar] [CrossRef]
- Mandell, R.B. Corneal power correction factor for photorefractive keratectomy. J. Refract. Corneal Surg. 1994, 10, 125–128. [Google Scholar] [PubMed]
- Kennedy, K.M.; Ford, C.; Kennedy, B.F.; Bush, M.B.; Sampson, D.D. Analysis of mechanical contrast in optical coherence elastography. J. Biomed. Opt. 2013, 18, 121508. [Google Scholar] [CrossRef] [PubMed]
- Hepburn, M.S.; Wijesinghe, P.; Chin, L.; Kennedy, B.F. Analysis of spatial resolution in phase-sensitive compression optical coherence elastography. Biomed. Opt. Express 2019, 10, 1496–1513. [Google Scholar] [CrossRef] [Green Version]
- Wollensak, G.; Spoerl, E.; Seiler, T. Stress-strain measurements of human and porcine corneas after riboflavin-ultraviolet-a-induced cross-linking. J. Cataract Refract. Surg. 2003, 29, 1780–1785. [Google Scholar] [CrossRef]
- Kirby, M.A.; Pelivanov, I.; Song, S.; Ambrozinski, L.; Yoon, S.J.; Gao, L.; Li, D.; Shen, T.T.; Wang, R.K.; O’Donnell, M. Optical coherence elastography in ophthalmology. J. Biomed. Opt. 2017, 22, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Singh, M.; Twa, M.D.; Larin, K.V. Optical coherence elastography for ocular biomechanics. In Biomechanics of the Eye; Roberts, C.J., Dupps, W.J., Downs, J.C., Eds.; Kugler Publications: Amsterdam, The Netherlands, 2018; pp. 117–145. [Google Scholar]
- Singh, M.; Han, Z.; Li, J.; Vantipalli, S.; Aglyamov, S.R.; Twa, M.D.; Larin, K.V. Quantifying the effects of hydration on corneal stiffness with noncontact optical coherence elastography. J. Cataract Refract. Surg. 2018, 44, 1023–1031. [Google Scholar] [CrossRef]
- Vantipalli, S.; Li, J.; Singh, M.; Aglyamov, S.R.; Larin, K.V.; Twa, M.D. Effects of thickness on corneal biomechanical properties using optical coherence elastography. Optom. Vis. Sci. 2018, 95, 299–308. [Google Scholar] [CrossRef]
- Seiler, T.G.; Fischinger, I.; Koller, T.; Zapp, D.; Frueh, B.E.; Seiler, T. Customized corneal cross-linking: One-year results. Am. J. Ophthalmol. 2016, 166, 14–21. [Google Scholar] [CrossRef]
- Roberts, C.J.; Dupps, W.J., Jr. Biomechanics of corneal ectasia and biomechanical treatments. J. Cataract Refract. Surg. 2014, 40, 991–998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kennedy, K.M.; Es’haghian, S.; Chin, L.; McLaughlin, R.A.; Sampson, D.D.; Kennedy, B.F. Optical palpation: Optical coherence tomography-based tactile imaging using a compliant sensor. Opt. Lett. 2014, 39, 3014–3017. [Google Scholar] [CrossRef] [PubMed]
- Baptista, A.M.; de Sousa, R.A.; Serra, P.M.; Abreu, C.M.; da Silva, C.M. Evaluation of discomfort of goldmann tonometry without anaesthetic. Ophthalmic Physiol. Opt. 2010, 30, 854–859. [Google Scholar] [CrossRef] [PubMed]
- De Stefano, V.S.; Ford, M.R.; Seven, I.; Dupps, W.J., Jr. Depth-dependent corneal biomechanical properties in normal and keratoconic subjects by optical coherence elastography. Transl. Vis. Sci. Technol. 2020, 9, 4. [Google Scholar] [CrossRef]
- Wang, S.; Singh, M.; Lopez, A.L., 3rd; Wu, C.; Raghunathan, R.; Schill, A.; Li, J.; Larin, K.V.; Larina, I.V. Direct four-dimensional structural and functional imaging of cardiovascular dynamics in mouse embryos with 1.5 MHz optical coherence tomography. Opt. Lett. 2015, 40, 4791–4794. [Google Scholar] [CrossRef]
- Nair, A.; Singh, M.; Aglyamov, S.; Larin, K.V. Heartbeat optical coherence elastography: Corneal biomechanics in vivo. J. Biomed. Opt. 2021, 26, 020502. [Google Scholar] [CrossRef] [PubMed]
- Dielemans, I.; Vingerling, J.R.; Hofman, A.; Grobbee, D.E.; de Jong, P.T. Reliability of intraocular pressure measurement with the goldmann applanation tonometer in epidemiological studies. Graefes Arch. Clin. Exp. Ophthalmol. 1994, 232, 141–144. [Google Scholar] [CrossRef] [Green Version]
- Sovetsky, A.A.; Matveyev, A.L.; Matveev, L.A.; Shabanov, D.V.; Zaitsev, V.Y. Manually-operated compressional optical coherence elastography with effective aperiodic averaging: Demonstrations for corneal and cartilaginous tissues. Laser Phys. Lett. 2018, 15, 085602. [Google Scholar] [CrossRef]
- Kling, S.; Remon, L.; Perez-Escudero, A.; Merayo-Lloves, J.; Marcos, S. Corneal biomechanical changes after collagen cross-linking from porcine eye inflation experiments. Investig. Ophthalmol. Vis. Sci. 2010, 51, 3961–3968. [Google Scholar] [CrossRef] [Green Version]
- Herber, R.; Francis, M.; Spoerl, E.; Pillunat, L.E.; Raiskup, F.; Sinha Roy, A. Comparison of waveform-derived corneal stiffness and stress-strain extensometry-derived corneal stiffness using different cross-linking irradiances: An experimental study with air-puff applanation of ex vivo porcine eyes. Graefes Arch. Clin. Exp. Ophthalmol. 2020, 258, 2173–2184. [Google Scholar] [CrossRef]
- Seifert, J.; Hammer, C.M.; Rheinlaender, J.; Sel, S.; Scholz, M.; Paulsen, F.; Schaffer, T.E. Distribution of young’s modulus in porcine corneas after riboflavin/uva-induced collagen cross-linking as measured by atomic force microscopy. PLoS ONE 2014, 9, e88186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schumacher, S.; Oeftiger, L.; Mrochen, M. Equivalence of biomechanical changes induced by rapid and standard corneal cross-linking, using riboflavin and ultraviolet radiation. Investig. Ophthalmol. Vis. Sci. 2011, 52, 9048–9052. [Google Scholar] [CrossRef] [Green Version]
- Scarcelli, G.; Kling, S.; Quijano, E.; Pineda, R.; Marcos, S.; Yun, S.H. Brillouin microscopy of collagen crosslinking: Noncontact depth-dependent analysis of corneal elastic modulus. Investig. Ophthalmol. Vis. Sci. 2013, 54, 1418–1425. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hatami-Marbini, H.; Etebu, E. Hydration dependent biomechanical properties of the corneal stroma. Exp. Eye Res. 2013, 116, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Kling, S.; Marcos, S. Effect of hydration state and storage media on corneal biomechanical response from in vitro inflation tests. J. Refract. Surg. 2013, 29, 490–497. [Google Scholar] [CrossRef] [Green Version]
- Hatami-Marbini, H.; Rahimi, A. Stiffening effects of riboflavin/uva corneal collagen cross-linking is hydration dependent. J. Biomech. 2015, 48, 1052–1057. [Google Scholar] [CrossRef]
- Dias, J.; Ziebarth, N.M. Impact of hydration media on ex vivo corneal elasticity measurements. Eye Contact Lens 2015, 41, 281–286. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.S.; Wang, S.; Singh, M.; Aglyamov, S.; Emelianov, S.; Twa, M.D.; Larin, K.V. Air-pulse oce for assessment of age-related changes in mouse cornea in vivo. Laser Phys. Lett. 2014, 11, 065601. [Google Scholar] [CrossRef]
- Knox Cartwright, N.E.; Tyrer, J.R.; Marshall, J. Age-related differences in the elasticity of the human cornea. Investig. Ophthalmol. Vis. Sci. 2011, 52, 4324–4329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoeltzel, D.A.; Altman, P.; Buzard, K.; Choe, K. Strip extensiometry for comparison of the mechanical response of bovine, rabbit, and human corneas. J. Biomech. Eng. 1992, 114, 202–215. [Google Scholar] [CrossRef] [PubMed]
- Pitre, J.J., Jr.; Kirby, M.A.; Li, D.S.; Shen, T.T.; Wang, R.K.; O’Donnell, M.; Pelivanov, I. Nearly-incompressible transverse isotropy (niti) of cornea elasticity: Model and experiments with acoustic micro-tapping oce. Sci. Rep. 2020, 10, 12983. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Larin, K.V. Shear wave imaging optical coherence tomography (swi-oct) for ocular tissue biomechanics. Opt. Lett. 2014, 39, 41–44. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.; Larin, K.V. Noncontact depth-resolved micro-scale optical coherence elastography of the cornea. Biomed. Opt. Express 2014, 5, 3807–3821. [Google Scholar] [CrossRef] [Green Version]
- Singh, M.; Li, J.; Han, Z.; Vantipalli, S.; Liu, C.H.; Wu, C.; Raghunathan, R.; Aglyamov, S.R.; Twa, M.D.; Larin, K.V. Evaluating the effects of riboflavin/uv-a and rose-bengal/green light cross-linking of the rabbit cornea by noncontact optical coherence elastography. Investig. Ophthalmol. Vis. Sci. 2016, 57, OCT112–OCT120. [Google Scholar] [CrossRef] [Green Version]
- Dias, J.; Diakonis, V.F.; Kankariya, V.P.; Yoo, S.H.; Ziebarth, N.M. Anterior and posterior corneal stroma elasticity after corneal collagen crosslinking treatment. Exp. Eye Res. 2013, 116, 58–62. [Google Scholar] [CrossRef] [Green Version]
- Hollman, K.W.; Emelianov, S.Y.; Neiss, J.H.; Jotyan, G.; Spooner, G.J.; Juhasz, T.; Kurtz, R.M.; O’Donnell, M. Strain imaging of corneal tissue with an ultrasound elasticity microscope. Cornea 2002, 21, 68–73. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Matveyev, A.L.; Matveev, L.A.; Gubarkova, E.V.; Sovetsky, A.A.; Sirotkina, M.A.; Gelikonov, G.V.; Zagaynova, E.V.; Gladkova, N.D.; Vitkin, A. Practical obstacles and their mitigation strategies in compressional optical coherence elastography of biological tissues. J. Innov. Opt. Health Sci. 2017, 10, 1742006. [Google Scholar] [CrossRef] [Green Version]
- Wijesinghe, P.; Sampson, D.D.; Kennedy, B.F. Computational optical palpation: A finite-element approach to micro-scale tactile imaging using a compliant sensor. J. R. Soc. Interface 2017, 14, 1–11. [Google Scholar] [CrossRef]
- Kurokawa, K.; Makita, S.; Hong, Y.J.; Yasuno, Y. Two-dimensional micro-displacement measurement for laser coagulation using optical coherence tomography. Biomed. Opt. Express 2015, 6, 170–190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elsheikh, A.; Anderson, K. Comparative study of corneal strip extensometry and inflation tests. J. R. Soc. Interface 2005, 2, 177–185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kennedy, B.F.; Koh, S.H.; McLaughlin, R.A.; Kennedy, K.M.; Munro, P.R.; Sampson, D.D. Strain estimation in phase-sensitive optical coherence elastography. Biomed. Opt. Express 2012, 3, 1865–1879. [Google Scholar] [CrossRef] [PubMed]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, M.; Nair, A.; Aglyamov, S.R.; Larin, K.V. Compressional Optical Coherence Elastography of the Cornea. Photonics 2021, 8, 111. https://doi.org/10.3390/photonics8040111
Singh M, Nair A, Aglyamov SR, Larin KV. Compressional Optical Coherence Elastography of the Cornea. Photonics. 2021; 8(4):111. https://doi.org/10.3390/photonics8040111
Chicago/Turabian StyleSingh, Manmohan, Achuth Nair, Salavat R. Aglyamov, and Kirill V. Larin. 2021. "Compressional Optical Coherence Elastography of the Cornea" Photonics 8, no. 4: 111. https://doi.org/10.3390/photonics8040111
APA StyleSingh, M., Nair, A., Aglyamov, S. R., & Larin, K. V. (2021). Compressional Optical Coherence Elastography of the Cornea. Photonics, 8(4), 111. https://doi.org/10.3390/photonics8040111







