Broadband Absorption in Patterned Metal/Weakly-Absorbing-Spacer/Metal with Graded Photonic Super-Crystal
Abstract
1. Introduction
2. Simulation Methods
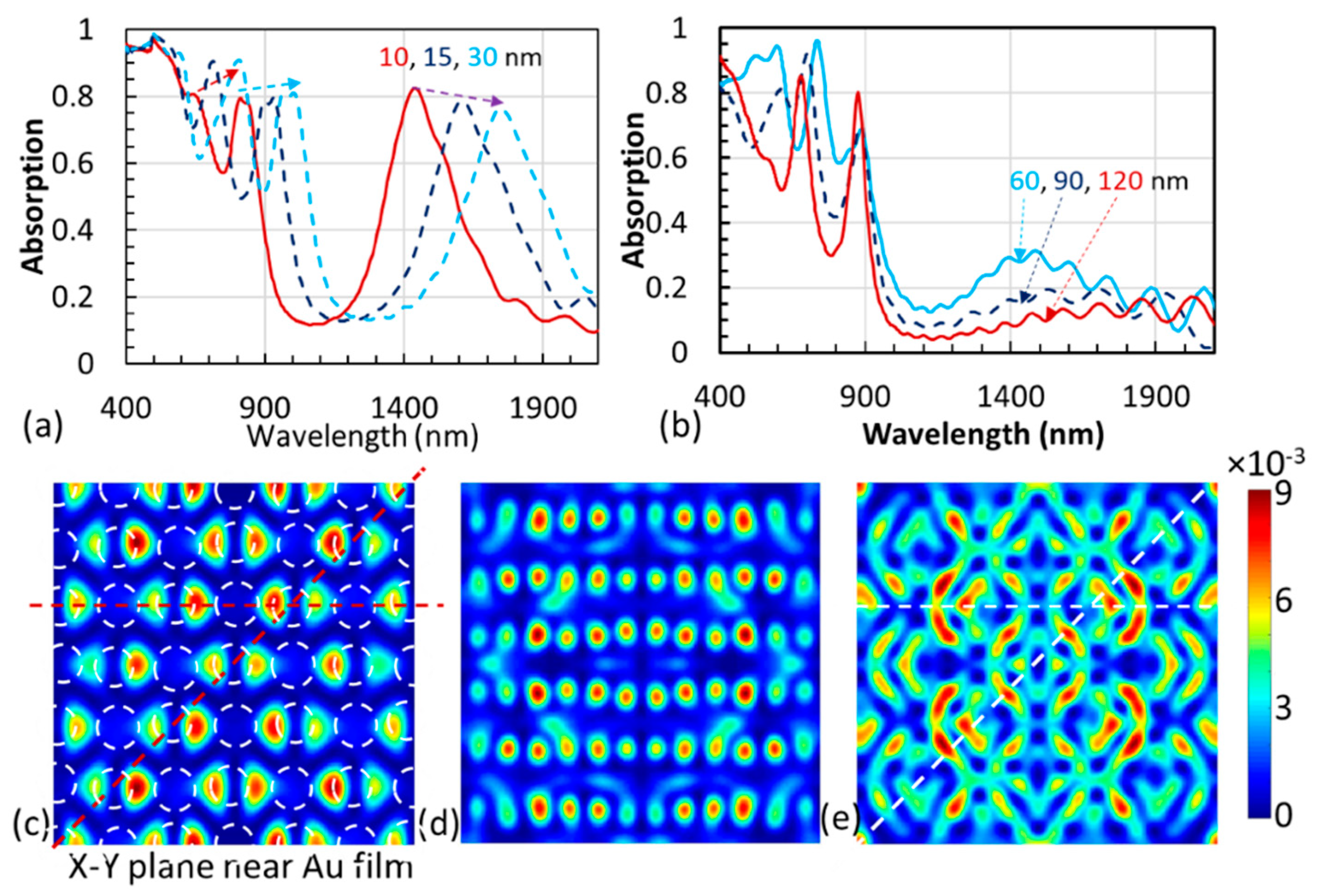
3. Multiple-Band Absorption in Au/SiO2/Au Patterned with GPSC
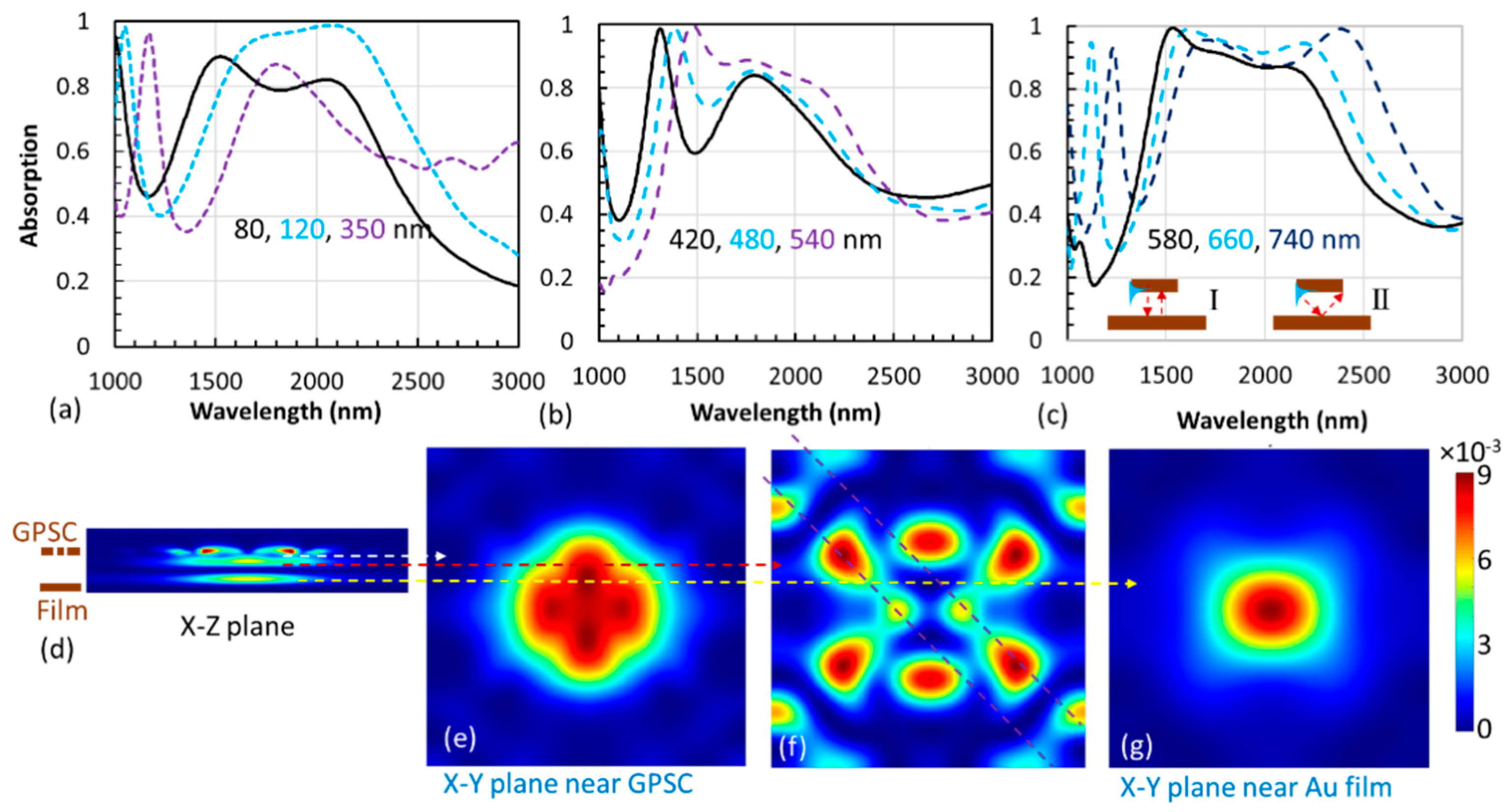
4. Broadband Absorption in Au/Absorbing-Spacer/Au Patterned with GPSC
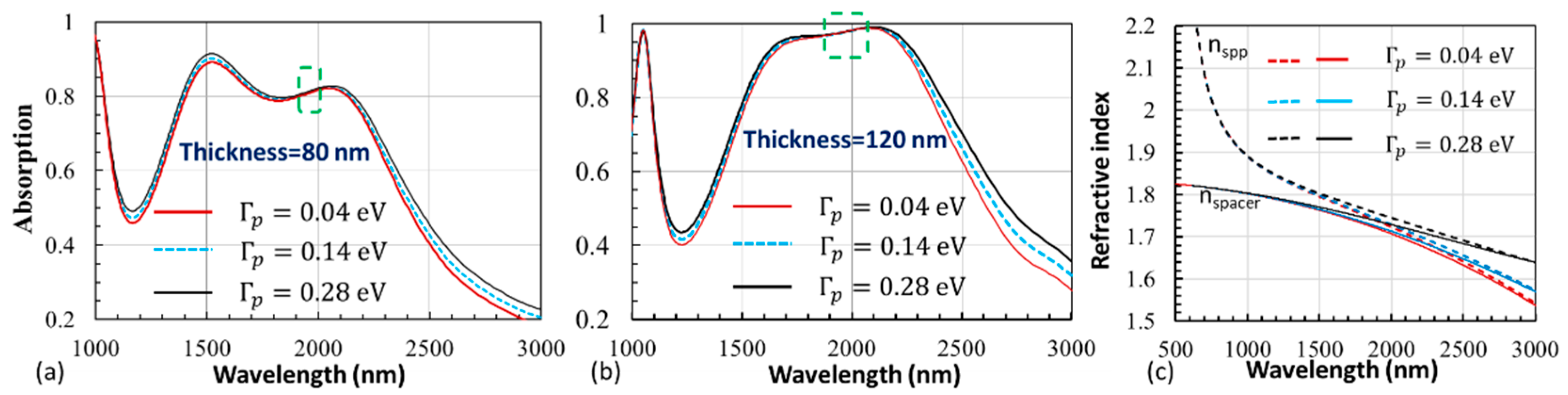
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, J.; Wang, Y.; Zhu, Y.; Zhang, W.; Yu, Y. Lithography-free flexible perfect broadband absorber in visible light based on an all-dielectric multilayer structure. Opt. Lett. 2020, 45, 5464–5467. [Google Scholar] [CrossRef]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef]
- Cao, J.; Sun, T.; Grattan, K.T.V. Gold nanorod-based localized surface plasmon resonance biosensors: A review. Sens. Actuators B Chem. 2014, 95, 332–351. [Google Scholar] [CrossRef]
- Chong, Y.D.; Cao, L.; Ge, H.; Stone, A.D. Coherent perfect absorbers: Time-reversed lasers. Phys. Rev. Lett. 2010, 105, 053901. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Zhen, Y.R.; Fan, L.; Zhu, X.; Nordlander, P. Tunable wide-angle plasmonic perfect absorber at visible frequencies. Phys. Rev. B 2012, 85, 245401. [Google Scholar] [CrossRef]
- Nielsen, M.G.; Pors, A.; Albrektsen, O.; Bozhevolnyi, S.I. Efficient absorption of visible radiation by gap plasmon resonators. Opt. Express 2012, 20, 13311–13319. [Google Scholar] [CrossRef] [PubMed]
- Luk, T.S.; Fofang, N.T.; Cruz-Campa, J.L.; Frank, I.; Campione, S. Surface Plasmon polariton enhanced ultrathin nano-structured CdTe solar cell. Opt. Express 2014, 22, A1372–A1379. [Google Scholar] [CrossRef] [PubMed]
- Chen, H. Interference theory of metamaterial perfect absorbers. Opt. Express 2012, 20, 7165–7172. [Google Scholar] [CrossRef]
- Aydin, K.; Ferry, E.V.; Briggs, M.R.; Atwater, H.A. Broadband polarization-independent resonant light absorption using ultrathin plasmonic super absorbers. Nat. Commun. 2011, 2, 517. [Google Scholar] [CrossRef]
- Sun, T.; Guo, C.F.; Cao, E.M.; Akinoglu, Y.; Wang, M.; Giersig, Z.R.; Kempa, K. A broadband solar absorber with 12 nm thick ultrathin a-Si layer by using random metallic nanomeshes. Appl. Phys. Lett. 2014, 104, 251119. [Google Scholar] [CrossRef]
- Sturmberg, B.C.P.; Chong, T.K.; Choi, D.Y.; White, T.P.; Botten, L.C.; Dossou, K.B.; Poulton, C.G.; Catchpole, K.R.; McPhedran, R.C.; de Sterke, C.M. Total absorption of visible light in ultrathin weakly absorbing semiconductor gratings. Optica 2016, 3, 556–562. [Google Scholar] [CrossRef]
- Ghobadi, A.; Hajian, H.; Rashed, A.R.; Butun, B.; Ozbay, E. Tuning the metal filling fraction in metal-insulator-metal ultra-broadband perfect absorbers to maximize the absorption bandwidth. Photon. Res. 2018, 6, 168–176. [Google Scholar] [CrossRef]
- Kats, M.A.; Blanchard, R.; Genevet, P.; Capasso, F. Nanometer optical coatings based on strong interference effects in highly absorbing media. Nat. Mater. 2013, 12, 20–24. [Google Scholar] [CrossRef]
- Kats, M.A.; Byrnes, S.J.; Blanchard, R.; Kolle, M.; Genevet, P.; Aizenberg, J.; Capasso, F. Enhancement of absorption and color contrast in ultra-thin highly absorbing optical coatings. Appl. Phys. Lett. 2013, 103, 101104. [Google Scholar] [CrossRef]
- Yongbing, L.; Runmei, S.; Qiwen, W.; Liang, S.; Bowen, L.; Wenhao, Z. Deducing critical coupling condition to achieve perfect absorption for thin-film absorbers and identifying key characteristics of absorbing materials needed for perfect Absorption. Appl. Phys. Lett. 2014, 104, 091109. [Google Scholar]
- Ding, B.; Qiu, M.; Blaikie, R.J. Manipulating light absorption in dye-doped dielectric films on reflecting surfaces. Opt. Express 2014, 22, 25965–25975. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Guo, L.; Liu, Z.; Liu, K.; Zeng, D.J.; Zhang, N.; Hu, H.; Jiang, S.; Gan, Q. Nanocavity enhancement for ultra-thin film optical absorber. Adv. Mater. 2014, 26, 2737–2743. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Butun, S.; Aydin, K. Large-area lithography-free super absorbers and color filters at visible frequencies using ultrathin metallic films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]
- Li, Z.; Palacios, E.; Butun, S.; Kocer, H.; Aydin, K. Omnidirectional broadband light absorption using large- area ultrathin lossy metallic film coatings. Sci. Rep. 2015, 5, 15137. [Google Scholar] [CrossRef]
- Lee, K.T.; Seo, S.; Lee, J.Y.; Guo, L.J. Strong resonance effect in a lossy medium-based optical cavity for angle robust spectrum filters. Adv. Mater. 2014, 26, 6324–6328. [Google Scholar] [CrossRef]
- Streyer, W.; Law, S.; Rooney, G.; Jacobs, T.; Wasserman, D. Strong absorption and selective emission from engineered metals with dielectric coatings. Opt. Express 2013, 21, 9113–9122. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.T.; Ji, C.; Guo, L.J. Wide-angle, polarization-independent ultrathin broadband visible absorbers. Appl. Phys. Lett. 2016, 108, 031107. [Google Scholar] [CrossRef]
- Kocer, H.; Butun, S.; Li, Z.; Aydin, K. Reduced near-infrared absorption using ultra-thin lossy metals in Fabry-Perot cavities. Sci. Rep. 2015, 5, 8157. [Google Scholar] [CrossRef] [PubMed]
- Mirshafieyan, S.S.; Luk, T.S.; Guo, J. Zeroth order Fabry-Perot resonance enabled ultra-thin perfect light absorber using percolation aluminum and silicon nanofilms. Opt. Mater. Express 2016, 6, 1032–1042. [Google Scholar] [CrossRef]
- Zhang, B.; Hendrickson, J.; Guo, J. Multispectral near perfect metamaterial absorbers using spatially multiplexed plasmon resonance metal square structures. J. Opt. Soc. Am. B 2013, 30, 656–662. [Google Scholar] [CrossRef]
- Hendrickson, J.; Guo, J.B.; Zhang, W.B.; Soref, R. Wideband perfect light absorber at midwave infrared using multiplexed metal structures. Opt. Lett. 2012, 37, 371–373. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Wang, C.; Lou, Y.; Cao, B.; Li, X. Near-perfect absorber with ultrawide bandwidth in infrared region using a periodically chirped structure. Opt. Commun. 2013, 305, 212. [Google Scholar] [CrossRef]
- Palanchoke, U.; Boutami, S.; Pocas, S.; Rochat, N.; Goudon, V.; Rabaud, W. Influence of dimensional variation of metal-insulator-metal stack in spectral response. Opt. Mater. Express 2018, 8, 2494–2509. [Google Scholar] [CrossRef]
- Nagarajan, A.; Vivek, K.; Shah, M.; Achanta, V.G.; Gerini, G. A Broadband Plasmonic Metasurface Superabsorber at Optical Frequencies: Analytical Design Framework and Demonstration. Adv. Opt. Mater. 2018, 6, 1800253. [Google Scholar] [CrossRef]
- Azad, A.K.; Kort-Kamp, W.J.M.; Sykora, M.; Weisse-Bernstein, N.R.; Luk, T.S.; Taylor, A.J.; Dalvit, D.A.R.; Chen, H. Metasurface Broadband Solar Absorber. Sci. Rep. 2016, 6, 20347. [Google Scholar] [CrossRef]
- Pors, A.; Albrektsen, O.; Radko, I.R.; Bozhevolnyi, S.I. Gap plasmon-based metasurfaces for total control of reflected light. Sci. Rep. 2013, 3, 2155. [Google Scholar] [CrossRef]
- Lowell, D.; Lutkenhaus, J.; George, D.; Philipose, U.; Chen, B.; Lin, Y. Simultaneous direct holographic fabrication of photonic cavity and graded photonic lattice with dual periodicity, dual basis, and dual symmetry. Opt. Express 2017, 25, 14444–14452. [Google Scholar] [CrossRef]
- Lowell, D.; Hassan, S.; Adewole, M.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-crystals using an integrated spatial light modulator and reflective optical element laser projection system. Appl. Opt. 2017, 56, 9888. [Google Scholar] [CrossRef]
- Lowell, D.; Hassan, S.; Sale, O.; Adewole, M.; Hurley, N.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-quasi-crystal with multiple level gradients. Appl. Opt. 2018, 57, 6598. [Google Scholar] [CrossRef]
- Hassan, S.; Sale, O.; Lowell, D.; Hurley, N.; Lin, Y. Holographic fabrication and optical property of graded photonic super-crystals with a rectangular unit super-cell. Photonics 2018, 5, 34. [Google Scholar] [CrossRef]
- Sale, O.; Hassan, S.; Hurley, N.; Alnasser, K.; Philipose, U.; Zhang, H.; Lin, Y. Holographic fabrication of octagon graded photonic super-crystal and potential applications in topological photonics. Front. Optoelectron. 2020, 13, 12–17. [Google Scholar] [CrossRef]
- Hassan, S.; Lowell, D.; Lin, Y. High light extraction efficiency into glass substrate in organic light-emitting diodes by patterning the cathode in graded superlattice with dual periodicity and dual basis. J. Appl. Phys. 2017, 121, 233104. [Google Scholar] [CrossRef]
- Hassan, S.; Alnasser, K.; Lowell, D.; Lin, Y. Effects of Photonic Band Structure and Unit Super-Cell Size in Graded Photonic Super-Crystal on Broadband Light Absorption in Silicon. Photonics 2019, 6, 50. [Google Scholar] [CrossRef]
- Hassan, S.; Sale, O.; Alnasser, K.; Hurley, N.; Zhang, H.; Philipose, U.; Lin, Y. Broadband light-matter interaction due to resonance cavities in graded photonic super-crystals. OSA Contin. 2019, 2, 3272–3280. [Google Scholar] [CrossRef]
- Hassan, S.; Lowell, D.; Adewole, M.; George, D.; Zhang, H.; Lin, Y. Extraordinary light trapping enhancement in silicon solar cell patterned with graded photonic super-crystal. Photonics 2017, 4, 50. [Google Scholar] [CrossRef]
- Alnasser, K.; Hassan, S.; Kamau, S.; Zhang, H.; Lin, Y. Enhanced light extraction from organic light emitting diodes by reducing plasmonic loss through graded photonic super-crystals. J. Opt. Soc. Am. B 2020, 37, 1283. [Google Scholar] [CrossRef]
- Hassan, S.; Jiang, Y.; Alnasser, K.; Hurley, N.; Zhang, H.; Philipose, U.; Lin, Y. Generation of over 1000 Diffraction Spots from 2D Graded Photonic Super-Crystals. Photonics 2020, 7, 27. [Google Scholar] [CrossRef]
- Rakic, A.; Djurisic, A.; Elazar, J.; Majewski, M. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271. [Google Scholar] [CrossRef] [PubMed]
- Oskooi, F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687. [Google Scholar] [CrossRef]
- Pors, A.; Bozhevolnyi, S.I. Plasmonic metasurfaces for efficient phase control in reflection. Opt. Express 2013, 21, 27438–27451. [Google Scholar] [CrossRef] [PubMed]
- Maradudin, A.A.; Sambles, J.R.; Barnes, W.L. Handbook of Surface Science Volume 4: Modern Plamnonics; Elsevier: Oxford, UK, 2014. [Google Scholar]
- Koechlin, C.; Bouchon, P.; Pardo, F.; Pelouard, J.-L.; Haïdar, R. Analytical description of subwavelength plasmonic MIM resonators and of their combination. Opt. Express 2013, 21, 7025–7032. [Google Scholar] [CrossRef]
- Toudert, J.; Serna, R.; Pardo, M.G.; Ramos, N.; Peláez, R.J.; Maté, B. Mid-to-far infrared tunable perfect absorption by a sub-λ/100 nanofilm in a fractal phasor resonant cavity. Opt. Express 2018, 26, 34043–34059. [Google Scholar] [CrossRef] [PubMed]
- Yu, P.; Besteiro, L.V.; Huang, Y.; Wu, J.; Fu, L.; Tan, H.H.; Jagadish, C.; Wiederrecht, G.P.; Govorov, A.O.; Wang, Z. Broadband metamaterial absorbers. Adv. Opt. Mater. 2019, 7, 1800995. [Google Scholar] [CrossRef]
- George, D.; Li, L.; Jiang, Y.; Lowell, D.; Mao, M.; Hassan, S.; Ding, J.; Cui, J.; Zhang, H.; Philipose, U.; et al. Localized Surface Plasmon Polariton Resonance in Holographically Structured Al-doped ZnO. J. Appl. Phys. 2016, 120, 043109. [Google Scholar] [CrossRef]
- Park, J.J.; Kang, X.; Liu, M.L. Brongersma. Electrically tunable Epsilon-NearZero (ENZ) metafilm absorbers. Sci. Rep. 2015, 5, 15754. [Google Scholar] [CrossRef] [PubMed]
- Evans, R.N.; Calhoun, S.R.; Brescia, J.R.; Cleary, J.W.; Smith, E.M.; Peale, R.E. Far-infrared bands in plasmonic metal-insulator-metal absorbers optimized for long-wave infrared. MRS Adv. 2019, 4, 667–674. [Google Scholar] [CrossRef]
- George, D.; Adewole, M.; Hassan, S.; Lowell, D.; Cui, J.; Zhang, H.; Philipose, U.; Lin, Y. Coupling of Surface Plasmon Polariton in Al-Doped ZnO with Fabry-Pérot Resonance for Total Light Absorption. Photonics 2017, 4, 35. [Google Scholar] [CrossRef]
- Nath, J.; Modak, S.; Rezadad, I.; Panjwani, D.; Rezaie, F.; Cleary, J.W.; Peale, R.E. Far-infrared absorber based on standing-wave resonances in metal-dielectric-metal cavity. Opt. Express 2015, 23, 20366–20380. [Google Scholar] [CrossRef]
- Cui, Y.; He, Y.; Jin, Y.; Ding, F.; Yang, L.; Ye, Y.; Zhong, S.; Lin, Y.; He, S. Plasmonic and Metamaterial Structures as Electromagnetic Absorbers. Laser Photonics Rev. 2014, 8, 495–520. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamau, S.; Hassan, S.; Alnasser, K.; Zhang, H.; Cui, J.; Lin, Y. Broadband Absorption in Patterned Metal/Weakly-Absorbing-Spacer/Metal with Graded Photonic Super-Crystal. Photonics 2021, 8, 114. https://doi.org/10.3390/photonics8040114
Kamau S, Hassan S, Alnasser K, Zhang H, Cui J, Lin Y. Broadband Absorption in Patterned Metal/Weakly-Absorbing-Spacer/Metal with Graded Photonic Super-Crystal. Photonics. 2021; 8(4):114. https://doi.org/10.3390/photonics8040114
Chicago/Turabian StyleKamau, Steve, Safaa Hassan, Khadijah Alnasser, Hualiang Zhang, Jingbiao Cui, and Yuankun Lin. 2021. "Broadband Absorption in Patterned Metal/Weakly-Absorbing-Spacer/Metal with Graded Photonic Super-Crystal" Photonics 8, no. 4: 114. https://doi.org/10.3390/photonics8040114
APA StyleKamau, S., Hassan, S., Alnasser, K., Zhang, H., Cui, J., & Lin, Y. (2021). Broadband Absorption in Patterned Metal/Weakly-Absorbing-Spacer/Metal with Graded Photonic Super-Crystal. Photonics, 8(4), 114. https://doi.org/10.3390/photonics8040114






