Correlation and Power Distribution of Intercore Crosstalk Field Components of Polarization-Coupled Weakly Coupled Single-Mode Multicore Fibres
Abstract
1. Introduction
2. ICXT Model and Computation of Mean ICXT Power in Single-Mode WC-MCFs
2.1. Evolution of Interfering and Interfered Fields in a Single-Mode WC-MCF
2.2. Computation of the Mean ICXT Power in a WC-MCF
3. Description of the Numerical Simulator and Assessment of the Number of Samples Required to Obtain Stabilized Estimates of the Mean ICXT Power
3.1. Brief Description about the Simulator Implementation
3.2. Dependence of Estimates of Mean ICXT Power on the Number of Samples
4. Parameters Used to Characterize the Statistical Properties of the ICXT Field Components
5. Numerical Results
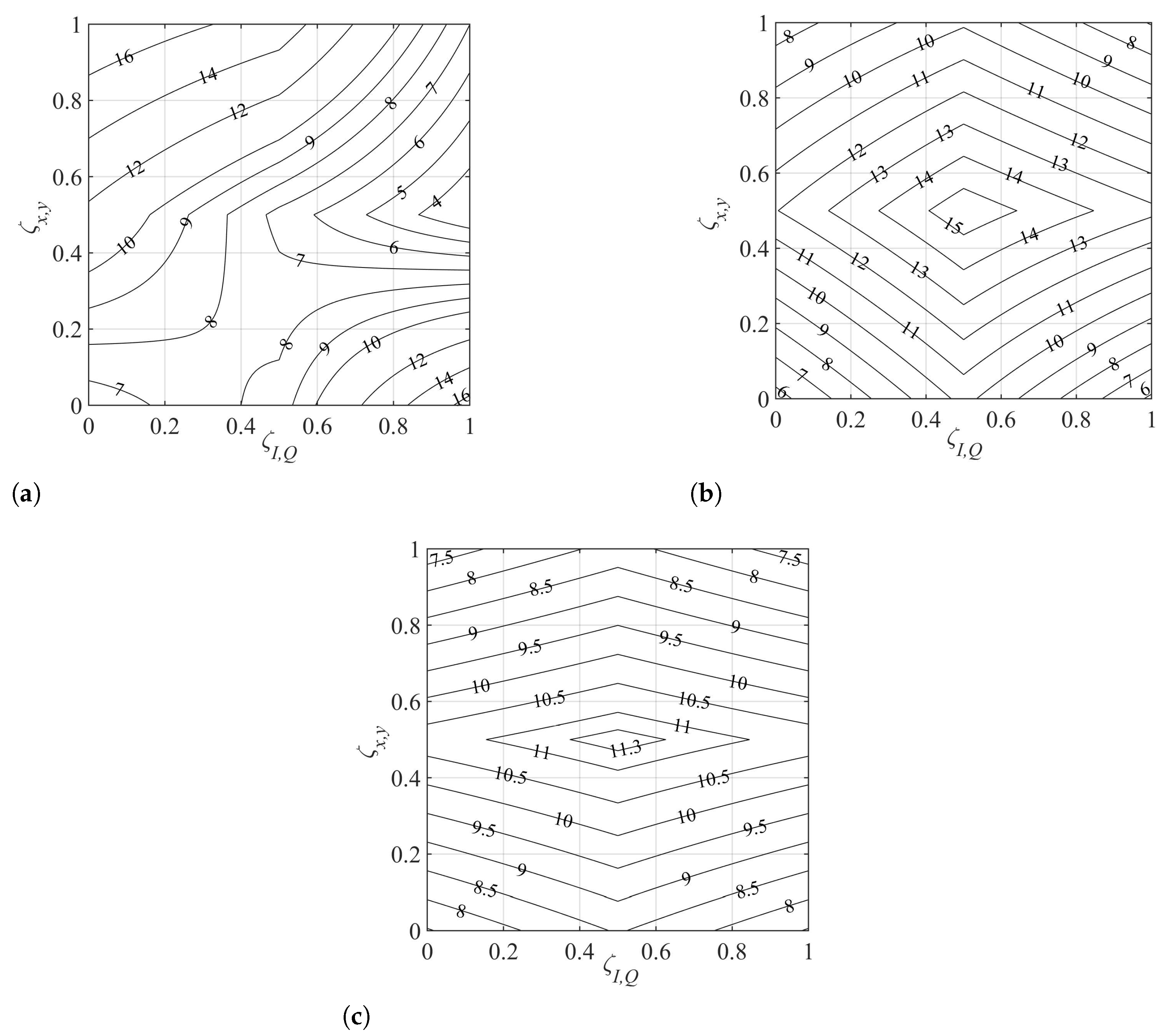
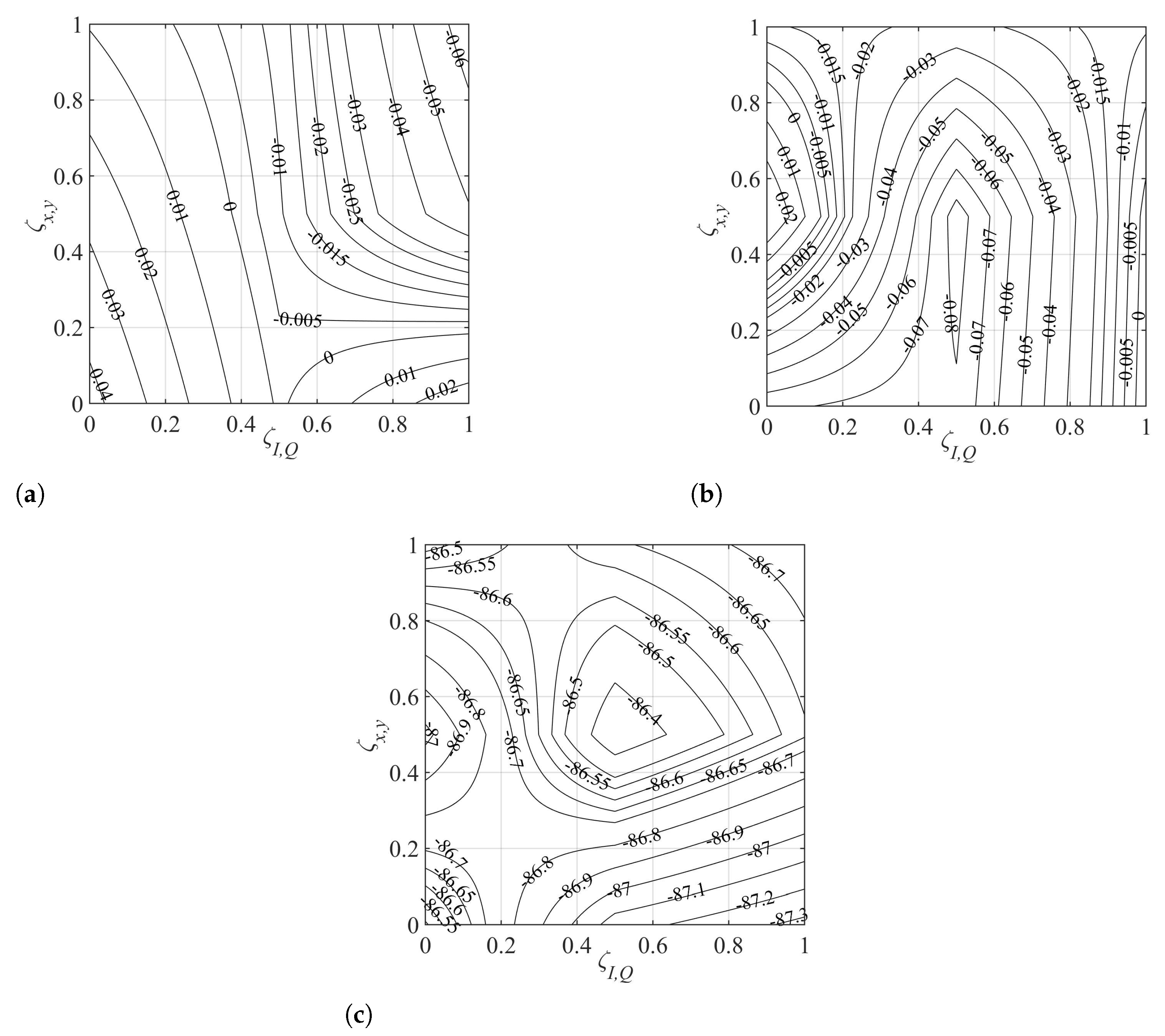
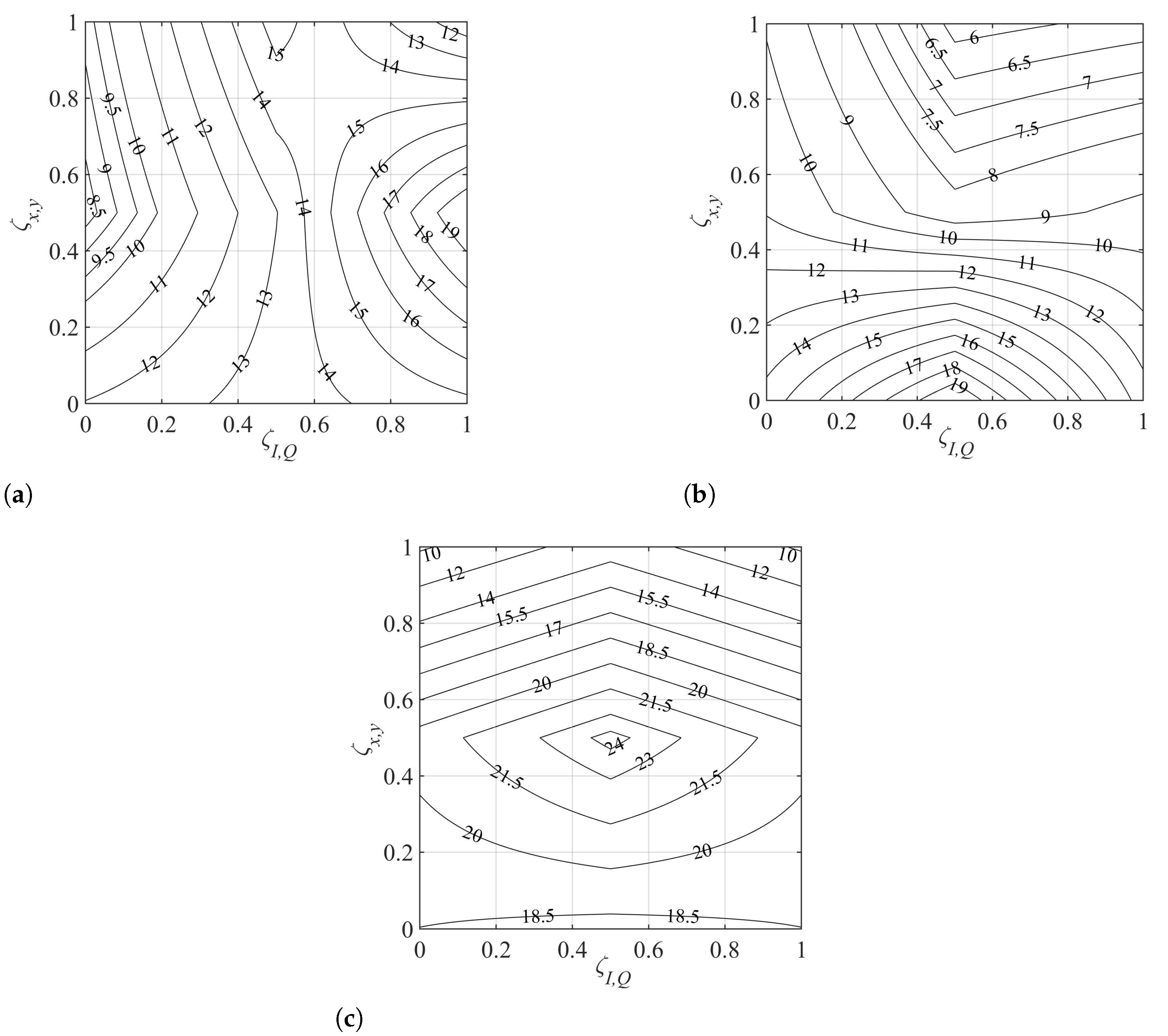
5.1. Results for Single-Mode Homogeneous WC-MCF
5.2. Results for Quasi-Homogeneous Single-Mode WC-MCF
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| CME | Coupled mode equations |
| CPU | Central processing unit |
| ICXT | Intercore crosstalk |
| MCF | Multicore fiber |
| OCS | Optical communication systems |
| PC | Personal computer |
| Probability density function | |
| RAM | Random access memory |
| RMM | Random modulus model |
| WC | Weakly coupled |
References
- Sano, A.; Takara, H.; Kobayashi, T.; Miyamoto, Y. Crosstalk-managed high capacity long haul multicore fiber transmission with propagation-direction interleaving. J. Lightw. Technol. 2014, 32, 2771–2779. [Google Scholar] [CrossRef]
- Sakaguchi, J.; Puttnam, B.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T.; Imamura, K.; Inaba, H.; Mukasa, K.; et al. 305 Tb/s space division multiple transmission using homogeneous 19-core fiber. J. Lightw. Technol. 2013, 31, 7554–7562. [Google Scholar] [CrossRef]
- Puttnam, B.; Luís, R.; Agrell, E.; Rademacher, G.; Sakaguchi, J.; Klaus, W.; Saridis, G.; Awaji, Y.; Wada, N. High capacity transmission systems using homogeneous multi-core fibers. J. Lightw. Technol. 2017, 35, 1157–1167. [Google Scholar] [CrossRef]
- Klaus, W.; Puttnam, B.J.; Luis, R.S.; Sakaguchi, J.; Mendinueta, J.D.; Awaji, Y.; Wada, N. Advanced space division multiplexing technologies for optical networks. IEEE/OSA J. Opt. Commun. Netw. 2017, 9, C1–C11. [Google Scholar] [CrossRef]
- Li, M.J.; Hayashi, T. Chapter 1—Advances in low-loss, large-area, and multicore fibers. In Optical Fiber Telecommunications VII; Willner, A.E., Ed.; Academic Press: Kolkata, India, 2020; pp. 3–50. [Google Scholar] [CrossRef]
- Tsuritani, T.; Soma, D.; Wakayama, Y.; Miyagawa, Y.; Takahashi, M.; Morita, I.; Maeda, K.; Kawasaki, K.; Matsuura, T.; Tsukamoto, M.; et al. Field test of installed high-density optical fiber cable with multi-core fibers toward practical deployment. In Optical Fiber Communication Conference (OFC) 2019; Optical Society of America: San Diego, CA, USA, 3–7 March 2019; p. M3J.4. [Google Scholar] [CrossRef]
- Hayashi, T.; Nagashima, T.; Muramoto, T.; Sato, F.; Nakanishi, T. Spatial mode dispersion suppressed randomly-coupled multi-core fiber in straightened loose-tube cable. In Optical Fiber Communication Conference Postdeadline Papers 2019; Optical Society of America: San Diego, CA, USA, 3–7 March 2019; p. Th4A.2. [Google Scholar] [CrossRef]
- Hayashi, T.; Nagashima, T.; Nakanishi, T.; Morishima, T.; Kawawada, R.; Mecozzi, A.; Antonelli, C. Field-deployed multi-core fiber testbed. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Fini, J.; Zhu, B.; Taunay, T.; Yan, M. Statistics of crosstalk in bent multicore fibers. Opt. Express 2010, 18, 15122–15129. [Google Scholar] [CrossRef]
- Takenaga, K.; Arakawa, Y.; Tanigawa, S.; Guan, N.; Matsuo, S.; Saitoh, K.; Koshiba, M. An investigation on crosstalk in multi-core fibers by introducing random fluctuation along longitudinal direction. IEICE Trans. Commun. 2011, 94-B, 409–416. [Google Scholar] [CrossRef]
- Hayashi, T.; Taru, T.; Shimakawa, O.; Sasaki, T.; Sasaoka, E. Design and fabrication of ultra-low crosstalk and low-loss multi-core fiber. Opt. Express 2011, 19, 16576–16592. [Google Scholar] [CrossRef]
- Koshiba, M.; Saitoh, K.; Takenaga, K.; Matsuo, S. Multi-core fiber design and analysis: Coupled-mode theory and coupled-power theory. Opt. Express 2011, 19, B102–B111. [Google Scholar] [CrossRef]
- Koshiba, M.; Saitoh, K.; Takenaga, K.; Matsuo, S. Analytical expression of average power-coupling coefficients for estimating intercore crosstalk in multicore fibers. IEEE Photonics J. 2012, 4, 1987–1995. [Google Scholar] [CrossRef]
- Hayashi, T.; Chen, H.; Fontaine, N.; Nagashima, T.; Ryf, R.; Essiambre, R.; Taru, T. Effects of core count/layout and twisting condition on spatial mode dispersion in coupled multi-core fibers. In Proceedings of the 42nd European Conference on Optical Communication, ECOC 2016, Düsseldorf, Germany, 18–22 September 2016; pp. 1–3. [Google Scholar]
- Fujisawa, T.; Amma, Y.; Sasaki, Y.; Matsuo, S.; Aikawa, K.; Saitoh, K.; Koshiba, M. Crosstalk analysis of heterogeneous multicore fibers using coupled-mode theory. IEEE Photonics J. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Cartaxo, A.; Alves, T. Discrete changes model of inter-core crosstalk of real homogeneous multi-core fibers. J. Lightw. Technol. 2017, 35, 2398–2408. [Google Scholar] [CrossRef]
- Soeiro, R.; Alves, T.; Cartaxo, A. Dual polarization discrete changes model of inter-core crosstalk in multi-core fibers. IEEE Photonics Technol. Lett. 2017, 29, 1395–1398. [Google Scholar] [CrossRef]
- Cartaxo, A.; Morgado, J. New expression for evaluating the mean crosstalk power in weakly-coupled multi-core fibers. J. Lightw. Technol. 2021, 39, 1830–1842. [Google Scholar] [CrossRef]
- Alves, T.; Soeiro, R.; Cartaxo, A. Probability distribution of intercore crosstalk in weakly coupled MCFs with multiple interferers. IEEE Photonics Technol. Lett. 2019, 31, 651–654. [Google Scholar] [CrossRef]
- Alves, T.; Cartaxo, A.; Rebola, J. Stochastic properties and outage in crosstalk-impaired OOK-DD weakly-coupled MCF applications with low and high skew×bit-rate. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–8. [Google Scholar] [CrossRef]
- Rebola, J.; Alves, T.; Cartaxo, A. Outage probability due to intercore crosstalk from multiple cores in short-reach networks. IEEE Photonics Technol. Lett. 2021, 33, 281–284. [Google Scholar] [CrossRef]
- Pinheiro, B.; Rebola, J.; Cartaxo, A. Analysis of inter-core crosstalk in weakly-coupled multi-core fiber coherent systems. J. Lightw. Technol. 2021, 39, 42–54. [Google Scholar] [CrossRef]
- Antonelli, C.; Riccardi, G.; Hayashi, T.; Mecozzi, A. Role of polarization-mode coupling in the crosstalk between cores of weakly-coupled multi-core fibers. Opt. Express 2020, 28, 12847–12861. [Google Scholar] [CrossRef]
- Antonelli, C.; Mecozzi, A.; Shtaif, M.; Winzer, P. Random coupling between groups of degenerate fiber modes in mode multiplexed transmission. Opt. Express 2013, 21, 9484–9490. [Google Scholar] [CrossRef]
- Macho, A.; Garcia-Meca, C.; Fraile-Peláez, F.; Morant, M.; Llorente, R. Birefringence effects in multi-core fiber: Coupled local-mode theory. Opt. Express 2016, 24, 21415–21434. [Google Scholar] [CrossRef]
- Antonelli, C.; Hayashi, T.; Mecozzi, A. Random polarization-mode coupling explains inter-core crosstalk in uncoupled multi-core fibers. In Proceedings of the 2020 European Conference on Optical Communications (ECOC), Brussels, Belgium, 6–10 December 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Luís, R.; Puttnam, B.; Cartaxo, A.; Klaus, W.; Delgado-Mendinueta, J.; Awaji, Y.; Wada, N.; Nakanishi, T.; Hayashi, T.; Sasaki, T. Time and modulation frequency dependence of crosstalk in homogeneous multi-core fibers. J. Lightw. Technol. 2016, 34, 441–447. [Google Scholar] [CrossRef]
- Soeiro, R.; Alves, T.; Cartaxo, A. Inter-core crosstalk in weakly coupled MCFs with arbitrary core layout and the effect of bending and twisting on the coupling coefficient. Opt. Express 2019, 27, 74–91. [Google Scholar] [CrossRef] [PubMed]
- Amma, Y.; Sasaki, Y.; Takenaga, K.; Matsuo, S.; Tu, J.; Saitoh, K.; Koshiba, M.; Morioka, T.; Miyamoto, Y. High-density multicore fiber with heterogeneous core arrangement. In Proceedings of the 2015 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 22–26 March 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Tu, J.; Saitoh, K.; Koshiba, M.; Takenaga, K.; Matsuo, S. Design and analysis of large-effective-area heterogeneous trench-assisted multi-core fiber. Opt. Express 2012, 20, 15157–15170. [Google Scholar] [CrossRef] [PubMed]
- Matsui, T.; Sagae, Y.; Sakamoto, T.; Nakajima, K. Design and applicability of multi-core fibers with standard cladding diameter. J. Lightw. Technol. 2020, 38, 6065–6070. [Google Scholar] [CrossRef]
- Puttnam, B.; Luís, R.; Klaus, W.; Sakaguchi, J.; Mendinueta, J.D.; Awaji, Y.; Wada, N.; Tamura, Y.; Tetsuya, H.; Hirano, M.; et al. 2.15 Pb/s transmission using a 22 core homogeneous single-mode multi-core fiber and wideband optical comb. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Hayashi, T.; Sasaki, T.; Sasaoka, E.; Saitoh, K.; Koshiba, M. Physical interpretation of intercore crosstalk in multicore fiber: Effects of macrobend, structure fluctuation, and microbend. Opt. Express 2013, 21, 5401–5412. [Google Scholar] [CrossRef] [PubMed]
- Gordon, J.P.; Kogelnik, H. PMD fundamentals: Polarization mode dispersion in optical fibers. Proc. Natl. Acad. Sci. USA 2000, 97, 4541–4550. [Google Scholar] [CrossRef]
- Galtarrossa, A.; Griggio, P.; Palmieri, L.; Pizzinat, A. Low-PMD spun fibers. In Polarization Mode Dispersion; Menyuk, C., Galtarrossa, A., Eds.; Optical and Fiber Communications Reports (OFCR); Springer Science+Business Media, Inc.: New York, NY, USA, 2005; pp. 246–276. [Google Scholar] [CrossRef]
- Wai, P.K.A.; Menyuk, C.R. Polarization decorrelation in optical fibers with randomly varying birefringence. Opt. Lett. 1994, 19, 1517–1519. [Google Scholar] [CrossRef]
- Galtarossa, A.; Palmieri, L.; Schiano, M.; Tambosso, T. Measurement of birefringence correlation length in long, single-mode fibers. Opt. Lett. 2001, 26, 962–964. [Google Scholar] [CrossRef]
- Galtarrossa, A.; Palmieri, L.; Pizzinat, A.; Marks, S.; Menyuk, C. An analytical formula for the mean differential group delay of randomly birefringent spun fibers. J. Lightw. Technol. 2003, 21, 1635–1643. [Google Scholar] [CrossRef]
- Greenside, H.; Helfand, E. Numerical integration of stochastic differential equations-II. Bell Syst. Technol. J. 1981, 60, 1927–1940. [Google Scholar] [CrossRef]
- Franz, J.; Jain, V. Optical Communications. In Components and Systems; Narosa Publishing House: Calcuta, India, 2000. [Google Scholar]
- Galtarossa, A.; Palmieri, L.; Schiano, M.; Tambosso, T. Measurements of beat length and perturbation length in long single-mode fibers. Opt. Lett. 2000, 25, 384–386. [Google Scholar] [CrossRef] [PubMed]
- Nelson, L.; Jopson, R. Introduction to polarization mode dispersion in optical systems. In Polarization Mode Dispersion; Menyuk, C., Galtarrossa, A., Eds.; Optical and Fiber Communications Reports (OFCR); Springer Science+Business Media, Inc.: New York, NY, USA, 2005; pp. 1–33. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables, and Stochastic Processes; Communications and Signal Processing; McGraw-Hill: Singapore, 1991. [Google Scholar]

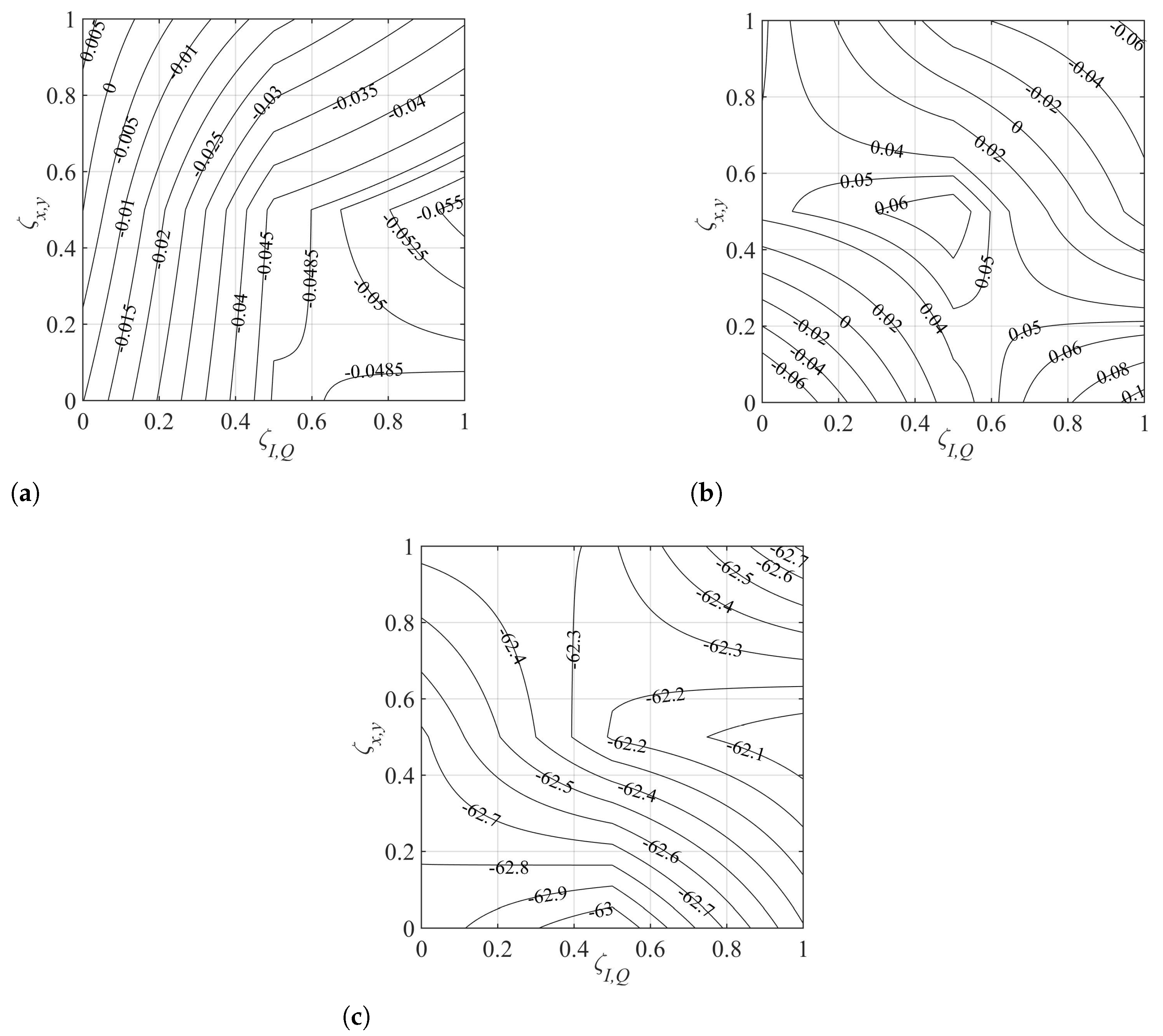
 ): 〈XTx,I〉; mark (
): 〈XTx,I〉; mark ( ): 〈XTx,Q〉; mark (
): 〈XTx,Q〉; mark ( ): 〈XTy,I〉; and mark (
): 〈XTy,I〉; and mark ( ): 〈XTy,Q〉.
): 〈XTy,Q〉.
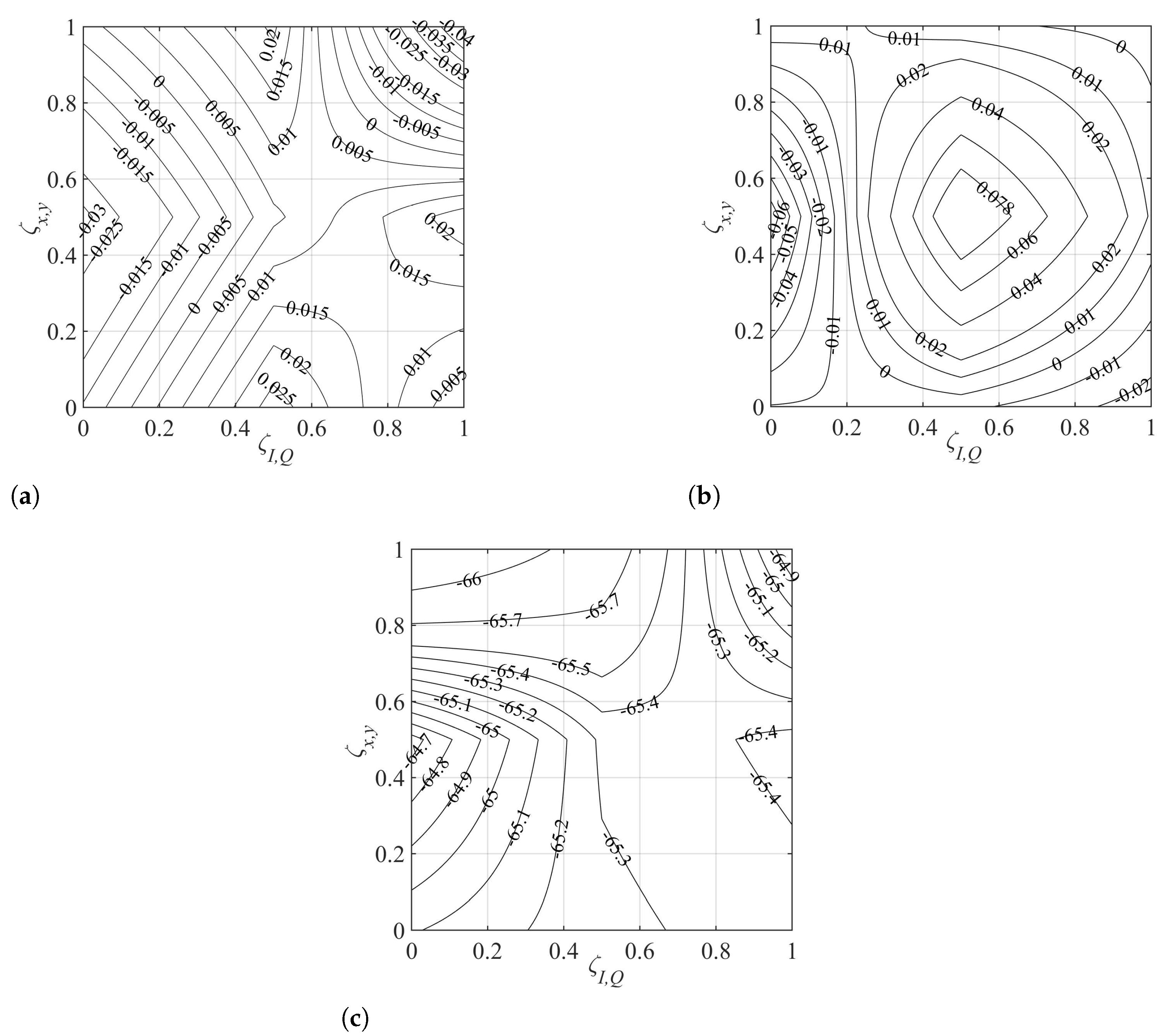
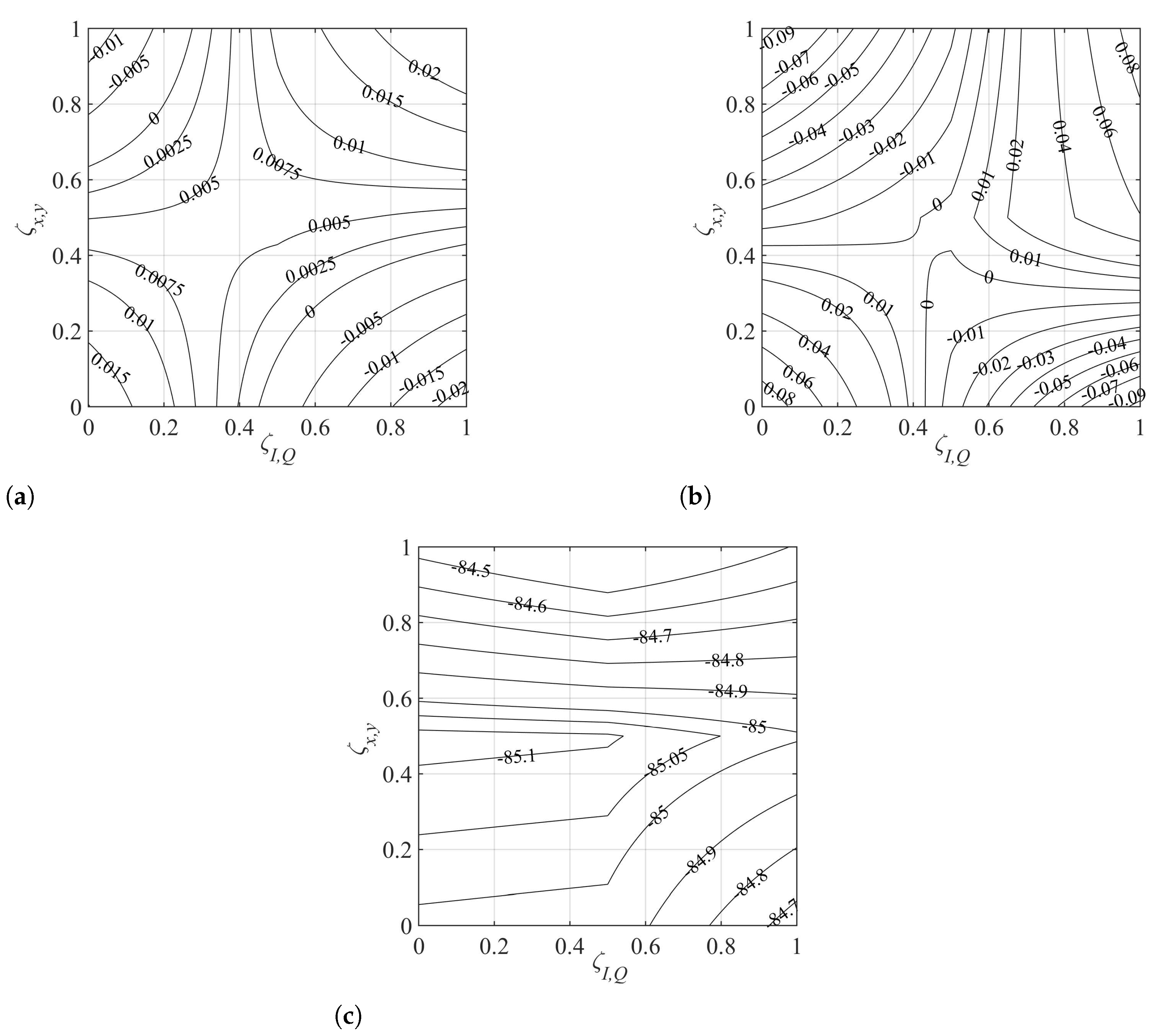
 ): 〈XTx,I〉; mark (
): 〈XTx,I〉; mark ( ): 〈XTx,Q〉; mark (
): 〈XTx,Q〉; mark ( ): 〈XTy,I〉; and mark (
): 〈XTy,I〉; and mark ( ): 〈XTy,Q〉.
): 〈XTy,Q〉.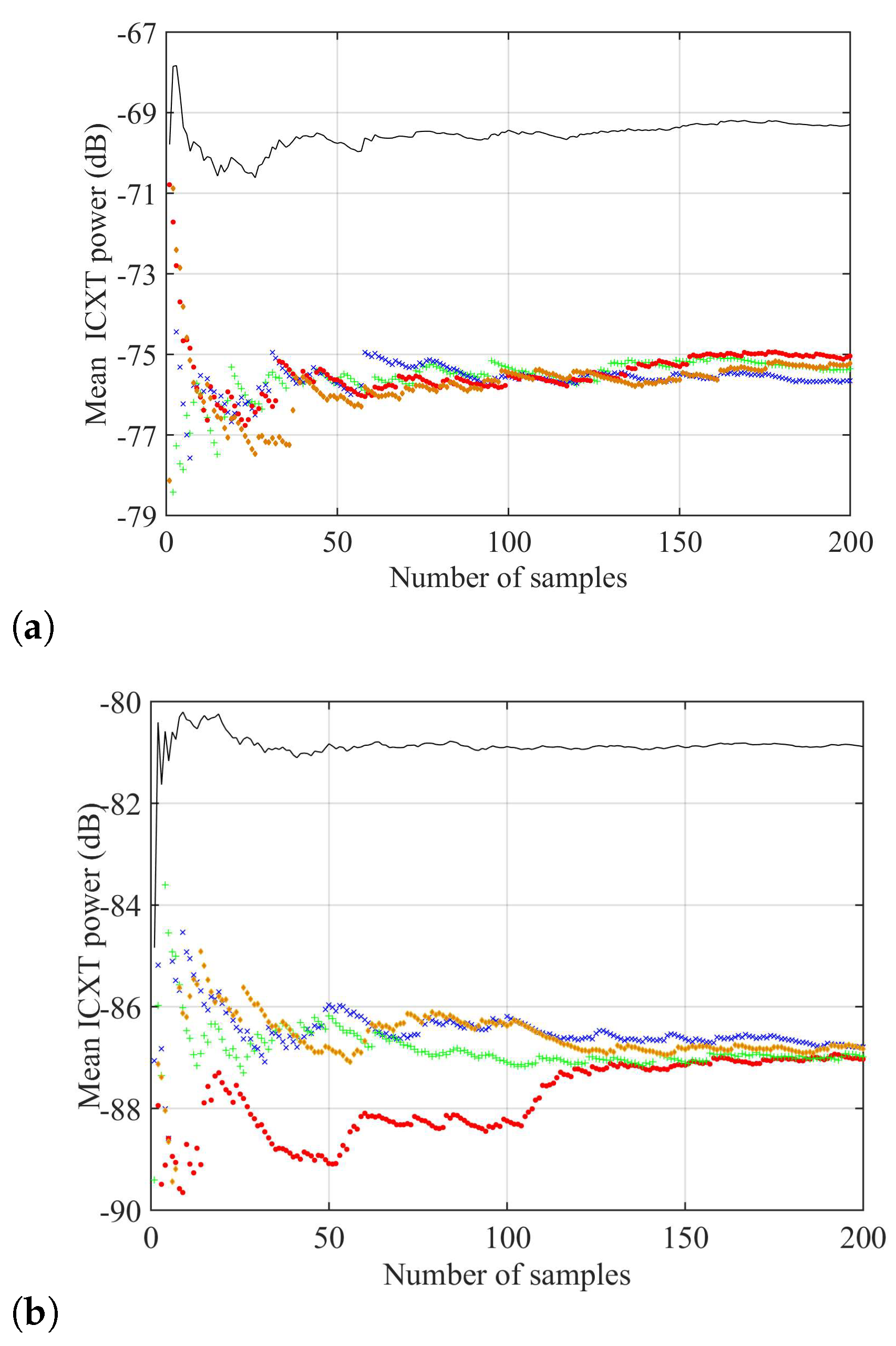
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morgado, J.A.P.; Cartaxo, A.V.T. Correlation and Power Distribution of Intercore Crosstalk Field Components of Polarization-Coupled Weakly Coupled Single-Mode Multicore Fibres. Photonics 2021, 8, 191. https://doi.org/10.3390/photonics8060191
Morgado JAP, Cartaxo AVT. Correlation and Power Distribution of Intercore Crosstalk Field Components of Polarization-Coupled Weakly Coupled Single-Mode Multicore Fibres. Photonics. 2021; 8(6):191. https://doi.org/10.3390/photonics8060191
Chicago/Turabian StyleMorgado, José A. P., and Adolfo V. T. Cartaxo. 2021. "Correlation and Power Distribution of Intercore Crosstalk Field Components of Polarization-Coupled Weakly Coupled Single-Mode Multicore Fibres" Photonics 8, no. 6: 191. https://doi.org/10.3390/photonics8060191
APA StyleMorgado, J. A. P., & Cartaxo, A. V. T. (2021). Correlation and Power Distribution of Intercore Crosstalk Field Components of Polarization-Coupled Weakly Coupled Single-Mode Multicore Fibres. Photonics, 8(6), 191. https://doi.org/10.3390/photonics8060191





