Nonlinear Dynamics of Two-State Quantum Dot Lasers under Optical Feedback
Abstract
:1. Introduction
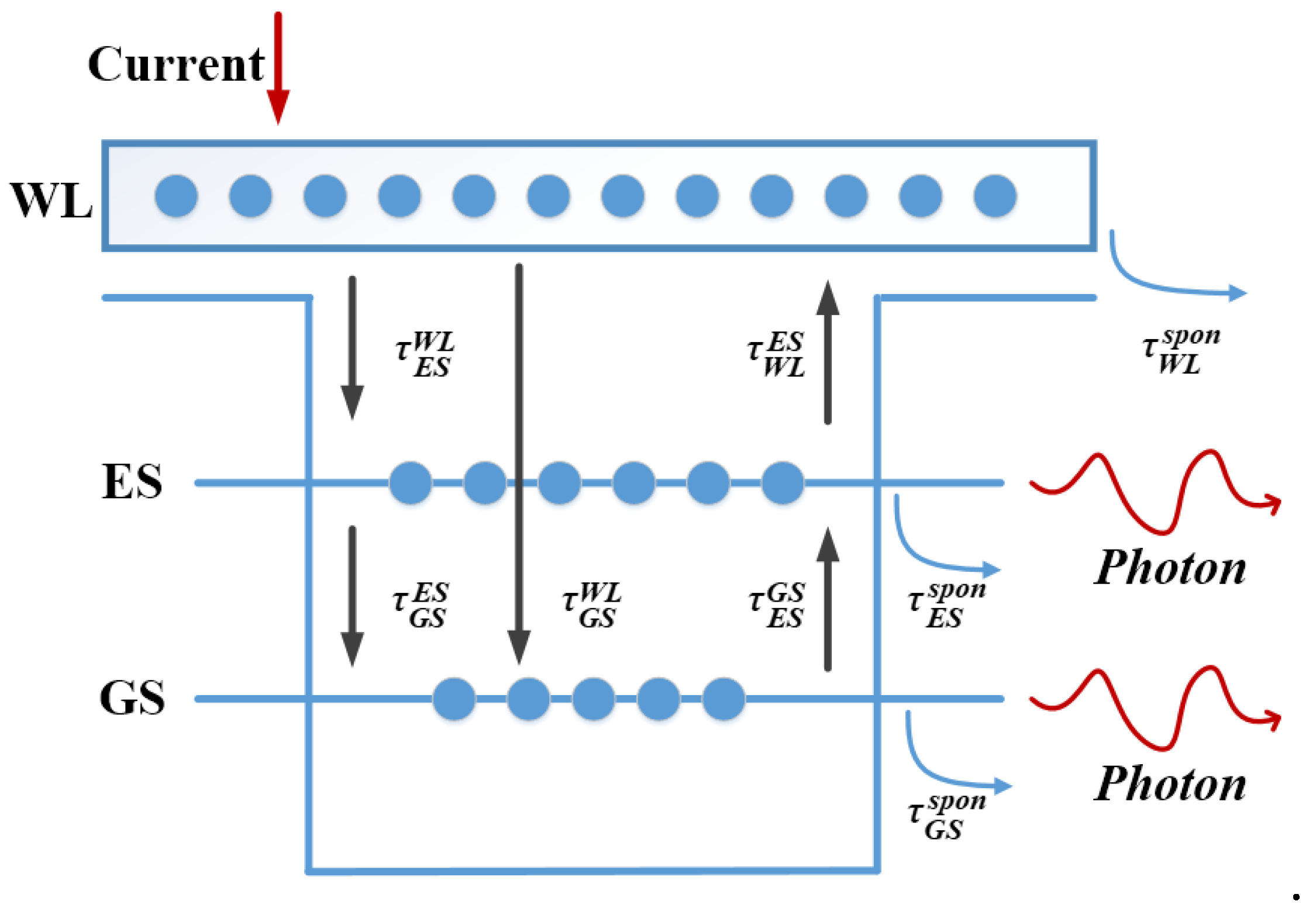
2. Rate Equation Model
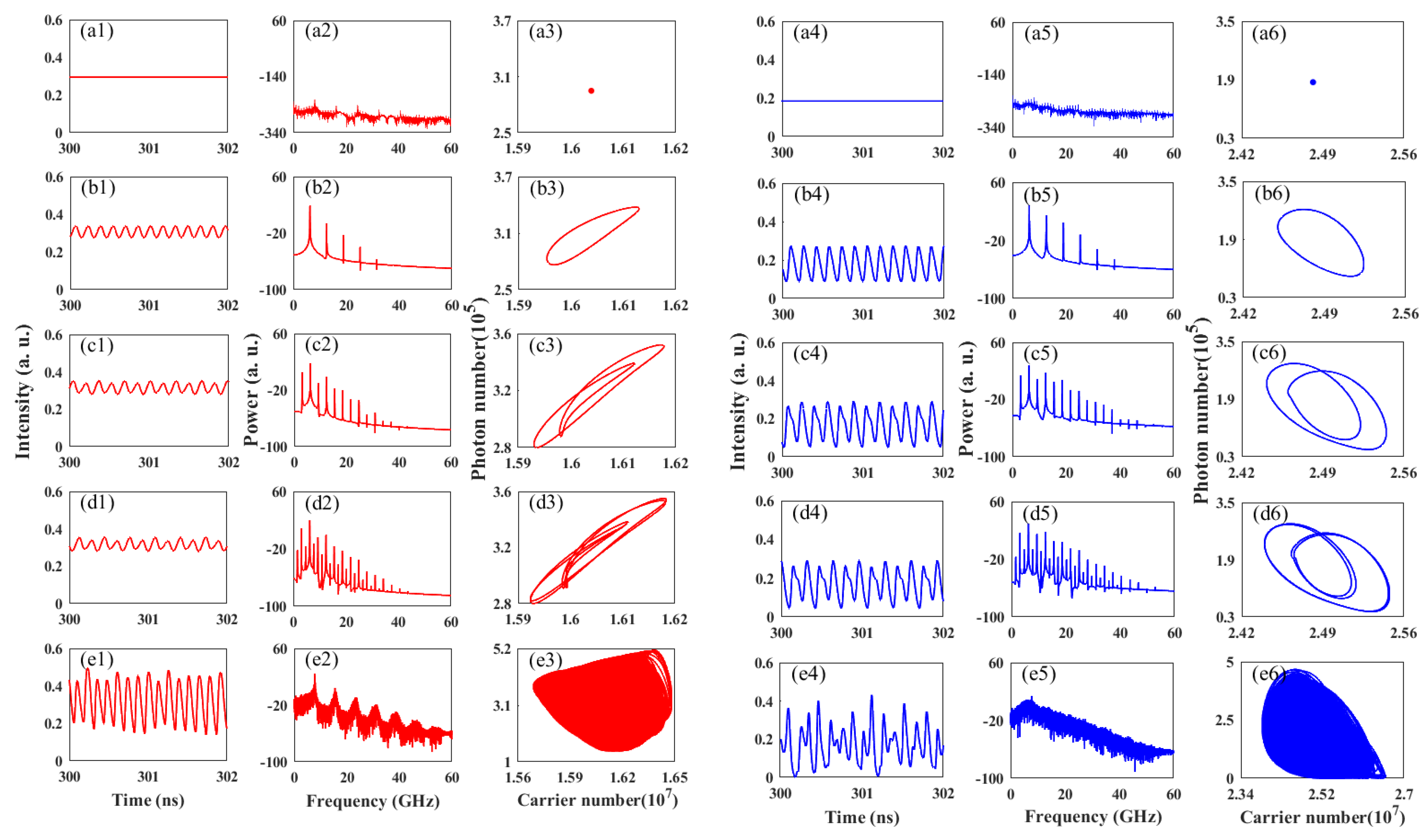
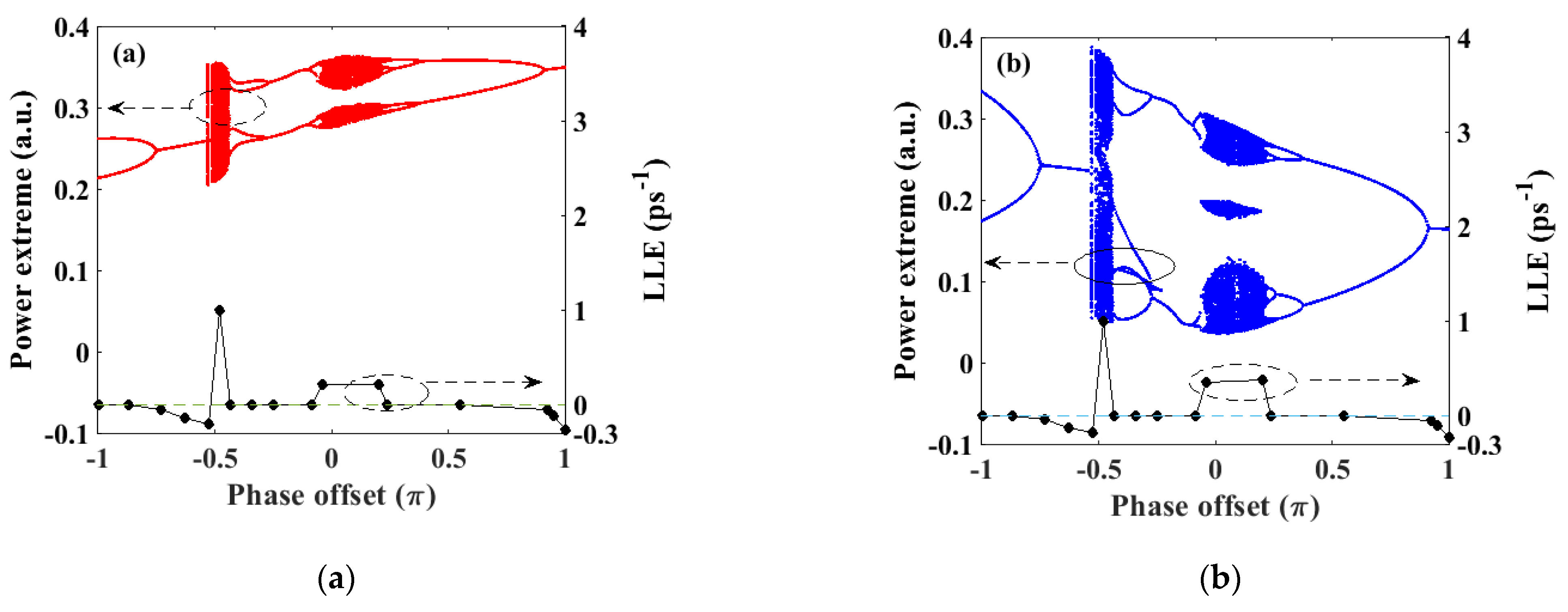
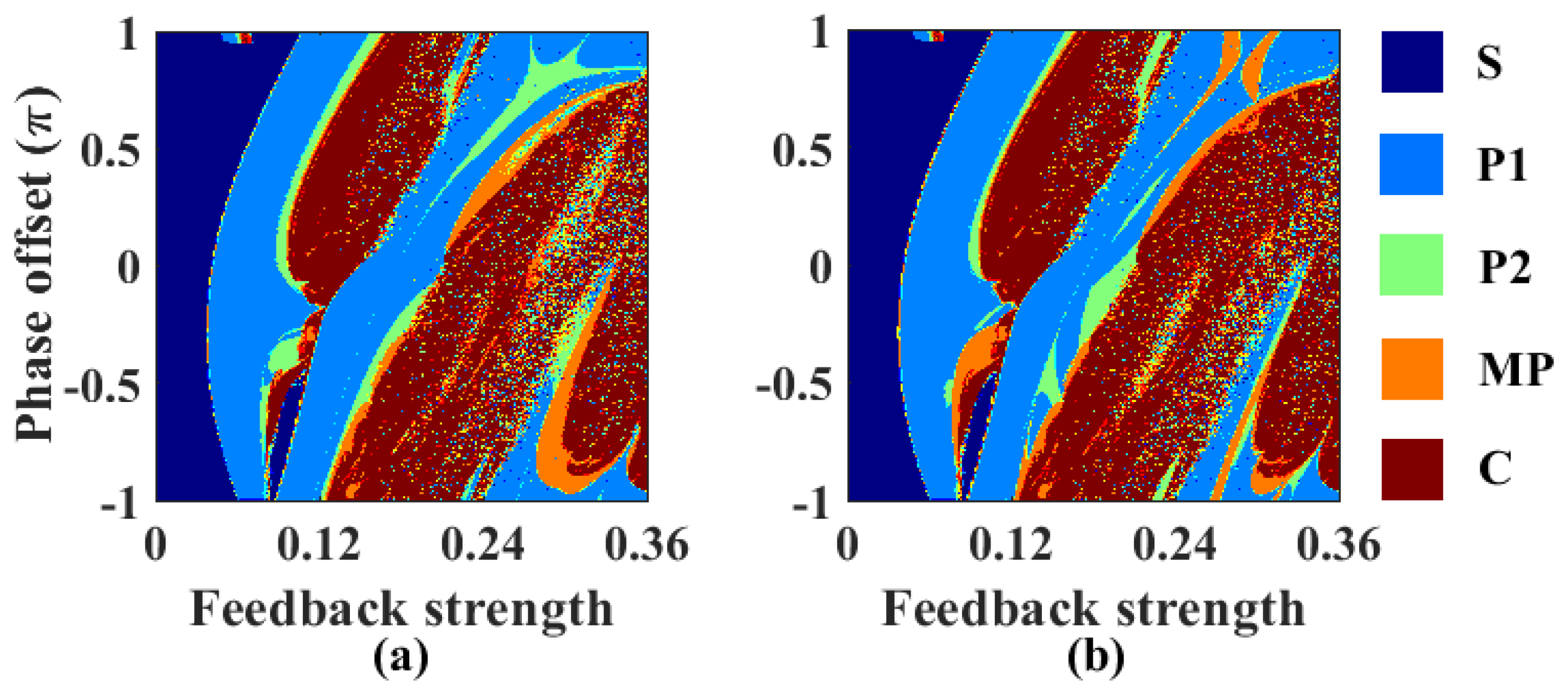
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, F.Y.; Tu, S.Y.; Huang, C.C.; Chang, S.M. Nonlinear dynamics of semiconductor lasers under repetitive optical pulse injection. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 604–611. [Google Scholar] [CrossRef]
- Yuan, G.H.; Yu, S.Y. Bistability and switching properties of semiconductor ring lasers with external optical injection. IEEE J. Quantum Electron. 2008, 44, 41–48. [Google Scholar] [CrossRef]
- Kawaguchi, Y.; Okuma, T.; Kanno, K.; Uchida, A. Entropy rate of chaos in an optically injected semiconductor laser for physical random number generation. Opt. Express 2021, 29, 2442–2457. [Google Scholar] [CrossRef] [PubMed]
- Jiang, N.; Xue, C.P.; Lv, Y.X.; Qiu, K. Physically enhanced secure wavelength division multiplexing chaos communication using multimode semiconductor lasers. Nonlinear Dyn. 2016, 86, 1937–1949. [Google Scholar] [CrossRef]
- Li, N.Q.; Pan, W.; Xiang, S.Y.; Yan, L.S.; Luo, B.; Zou, X.H.; Zhang, L.Y.; Mu, P.H. Photonic generation of wideband time-delay-signature-eliminated chaotic signals utilizing an optically injected semiconductor laser. IEEE J. Quantum Electron. 2012, 48, 1339–1345. [Google Scholar] [CrossRef]
- Salvide, M.F.; Masoller, C.; Torre, M.S. All-optical stochastic logic gate based on a VCSEL with tunable optical injection. IEEE J. Quantum Electron. 2013, 49, 886–893. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.X.; Xiang, S.Y.; Zhang, Y.H.; Lin, L.; Wen, A.J.; Hao, Y. Polarization multiplexing reservoir computing based on a VCSEL with polarized optical feedback. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1700109. [Google Scholar] [CrossRef]
- Liu, G.T.; Stintz, A.; Li, H.; Malloy, K.J.; Lester, L.F. Extremely low room-temperature threshold current density diode lasers using InAs dots in In0.15Ga0.85As quantum well. Electron. Lett. 1999, 35, 1163–1165. [Google Scholar] [CrossRef] [Green Version]
- Mikhrin, S.S.; Kovsh, A.R.; Krestnikov, I.L.; Kozhukhov, A.V.; Livshits, D.A.; Ledentsov, N.N.; Shernyakov, Y.M.; Novikov, I.I.; Maximov, M.V.; Ustinov, V.M.; et al. High power temperature-insensitive 1.3 μm InAs/InGaAs/GaAs quantum dot lasers. Semicond. Sci. Technol. 2005, 20, 340–342. [Google Scholar] [CrossRef]
- Saito, H.; Nishi, K.; Kamei, A.; Sugou, S. Low chirp observed in directly modulated quantum dot lasers. IEEE Photonics Technol. Lett. 2000, 12, 1298–1300. [Google Scholar] [CrossRef]
- Kuntz, M.; Fiol, G.; Lammlin, M.; Schubert, C.; Kovsh, A.R.; Jacob, A.; Umbach, A.; Bimberg, D. 10Gb/s data modulation using 1.3 μm InGaAs quantum dot lasers. Electron. Lett. 2005, 41, 244–245. [Google Scholar] [CrossRef]
- Norman, J.C.; Jung, D.; Zhang, Z.Y.; Wan, Y.T.; Liu, S.T.; Shang, C.; Herrick, R.W.; Chow, W.W.; Gossard, A.C.; Bowers, J.E. A review of high-performance quantum dot lasers on silicon. IEEE J. Quantum Electron. 2019, 55, 2000511. [Google Scholar] [CrossRef]
- Norman, J.C.; Jung, D.; Wan, Y.T.; Bowers, J.E. Perspective: The future of quantum dot photonic integrated circuits. APL Photonics 2018, 3, 030901. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, A.E.; Kovsh, A.R. Quantum dot diode lasers for optical communication systems. Quantum Electron. 2008, 38, 409–423. [Google Scholar] [CrossRef]
- Wang, C.; Raghunathan, R.; Schires, K.; Chan, S.C.; Lester, L.F.; Grillot, F. Optically injected InAs/GaAs quantum dot laser for tunable photonic microwave generation. Opt. Lett. 2016, 41, 1153–1156. [Google Scholar] [CrossRef]
- Jiang, Z.F.; Wu, Z.M.; Yang, W.Y.; Hu, C.X.; Lin, X.D.; Jin, Y.H.; Dai, M.; Cui, B.; Yue, D.Z.; Xia, G.Q. Numerical simulations on narrow-linewidth photonic microwave generation based on a QD laser simultaneously subject to optical injection and optical feedback. Appl. Opt. 2020, 59, 2935–2941. [Google Scholar] [CrossRef]
- Viktorov, E.A.; Mandel, P.; Tanguy, Y.; Houlihan, J.; Huyet, G. Electron-hole asymmetry and two-state lasing in quantum dot lasers. Appl. Phys. Lett. 2005, 87, 053113. [Google Scholar] [CrossRef] [Green Version]
- Meinecke, S.; Lingnau, B.; Rohm, A.; Ludge, K. Stability of optically injected two-state quantum-dot lasers. Ann. Phys. 2017, 529, 1600279. [Google Scholar] [CrossRef]
- Li, Q.Z.; Wang, X.; Zhang, Z.Y.; Chen, H.M.; Huang, Y.Q.; Hou, C.C.; Wang, J.; Zhang, R.Y.; Ning, J.Q.; Min, J.H.; et al. Development of modulation p-doped 1310 nm InAs/GaAs quantum dot laser materials and ultrashort cavity Fabry-Perot and distributed-feedback laser diodes. ACS Photonics 2018, 5, 1084–1093. [Google Scholar] [CrossRef]
- Grillot, F.; Norman, J.C.; Duan, J.; Zhang, Z.; Dong, B.; Huang, H.; Chow, W.W.; Bowers, J.E. Physics and applications of quantum dot lasers for silicon photonics. J. Nanophotonics 2020, 9, 1271–1286. [Google Scholar] [CrossRef]
- O’Brien, D.; Hegarty, S.P.; Huyet, G.; McInerney, J.G.; Kettler, T.; Laemmlin, M.; Bimberg, D.; Ustinov, V.M.; Zhukov, A.E.; Mikhrin, S.S.; et al. Feedback sensitivity of 1.3 mu m InAs/GaAs quantum dot lasers. Electron. Lett. 2003, 39, 1819–1820. [Google Scholar] [CrossRef]
- Huyet, G.; O’Brien, D.; Hegarty, S.P.; McInerney, J.G.; Uskov, A.V.; Bimberg, D.; Ribbat, C.; Ustinov, V.M.; Zhukov, A.E.; Mikhrin, S.S.; et al. Quantum dot semiconductor lasers with optical feedback. Phys. Status Solidi A 2003, 201, 345–352. [Google Scholar] [CrossRef]
- Stevens, B.J.; Childs, D.T.D.; Shahid, H.; Hogg, R.A. Direct modulation of excited state quantum dot lasers. Appl. Phys. Lett. 2009, 95, 061101. [Google Scholar] [CrossRef]
- Lee, C.S.; Bhattacharya, P.; Frost, T.; Guo, W. Characteristics of a high speed 1.22μm tunnel injection p-doped quantum dot excited state laser. Appl. Phys. Lett. 2011, 98, 011103. [Google Scholar] [CrossRef] [Green Version]
- Lin, L.C.; Chen, C.Y.; Huang, H.M.; Arsenijevic, D.; Bimberg, D.; Grillot, F.; Lin, F.Y. Comparison of optical feedback dynamics of InAs/GaAs quantum-dot lasers emitting solely on ground or excited states. Opt. Lett. 2018, 43, 210–213. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.F.; Wu, Z.M.; Jayaprasath, E.; Yang, W.Y.; Hu, C.X.; Xia, G.Q. Nonlinear dynamics of exclusive excited-state emission quantum dot lasers under optical injection. Photonics 2019, 6, 58. [Google Scholar] [CrossRef] [Green Version]
- Xu, P.F.; Yang, T.; Ji, H.M.; Cao, Y.L.; Gu, Y.X.; Liu, Y.; Ma, W.Q.; Wang, Z.G. Temperature-dependent modulation characteristics for 1.3 μm InAs/GaAs quantum dot lasers. J. Appl. Phys. 2010, 107, 013102. [Google Scholar]
- Pawlus, R.; Columbo, L.L.; Bardella, P.; Breuer, S.; Gioannini, M. Intensity noise behavior of an InAs/InGaAs quantum dot laser emitting on ground states and excited states. Opt. Lett. 2018, 43, 867–870. [Google Scholar] [CrossRef] [PubMed]
- Naderi, N.A.; Grillot, F.; Yang, K.; Wright, J.B.; Gin, A.; Lester, L.F. Two-color multi-section quantum dot distributed feedback laser. Opt. Express 2010, 18, 27028–27035. [Google Scholar] [CrossRef] [PubMed]
- Cataluna, M.A.; Nikitichev, D.I.; Mikroulis, S.; Simos, H.; Simos, C.; Mesaritakis, C.; Syvridis, D.; Krestnikov, I.; Livshits, D.; Rafailov, E.U. Dual-wavelength mode-locked quantum-dot laser, via ground and excited state transitions: Experimental and theoretical investigation. Opt. Express 2012, 18, 12832–12838. [Google Scholar] [CrossRef] [Green Version]
- Breuer, S.; Rossetti, M.; Drzewietzki, L.; Bardella, P.; Montrosset, I.; Elsasser, W. Joint experimental and theoretical investigations of two state mode locking in a strongly chirped reverse biased monolithic quantum dot laser. IEEE J. Quantum Electron. 2011, 47, 1320–1329. [Google Scholar] [CrossRef]
- Mesaritakis, C.; Kapsalis, A.; Bogris, A.; Syvridis, D. Artificial neuron based on integrated semiconductor quantum dot mode-locked lasers. Sci. Rep. 2016, 6, 39317. [Google Scholar] [CrossRef] [PubMed]
- Tykalewicz, B.; Goulding, D.; Hegarty, S.P.; Huyet, G.; Byrne, D.; Phelan, R.; Kelleher, B. All-optical switching with a dual-state, single-section quantum dot laser via optical injection. Opt. Lett. 2014, 39, 4607–4610. [Google Scholar] [CrossRef]
- Viktorov, E.A.; Dubinkin, I.; Fedorov, N.; Erneux, T.; Tykalewicz, B.; Hegarty, S.P.; Huyet, G.; Goulding, D.; Kelleher, B. Injection-induced, tunable, all-optical gating in a two-state quantum dot laser. Opt. Lett. 2016, 41, 3555–3558. [Google Scholar] [CrossRef] [Green Version]
- Tykalewicz, B.; Goulding, D.; Hegarty, S.P.; Huyet, G.; Dubinkin, I.; Fedorov, N.; Erneux, T.; Viktorov, E.A.; Kelleher, B. Optically induced hysteresis in a two-state quantum dot laser. Opt. Lett. 2016, 41, 1034–1037. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.F.; Wu, Z.M.; Jayaprasath, E.; Yang, W.Y.; Hu, C.X.; Cui, B.; Xia, G.Q. Power-induced lasing state switching and bistability in a two-state quantum dot laser subject to optical injection. Opt. Appl. 2020, 50, 257–269. [Google Scholar]
- Virte, M.; Breuer, S.; Sciamanna, M.; Panajotov, K. Switching between ground and excited states by optical feedback in a quantum dot laser diode. Appl. Phys. Lett. 2014, 105, 121109. [Google Scholar] [CrossRef]
- Virte, M.; Panajotov, K.; Sciamanna, M. Mode competition induced by optical feedback in two-color quantum dot lasers. IEEE J. Quantum Electron. 2013, 49, 578–585. [Google Scholar] [CrossRef]
- Virte, M.; Pawlus, R.; Sciamanna, M.; Panajotov, K.; Breuer, S. Energy exchange between modes in a multimode two-color quantum dot laser with optical feedback. Opt. Lett. 2016, 41, 3205–3208. [Google Scholar] [CrossRef]
- Meinecke, S.; Kluge, L.; Hausen, J.; Lingnau, B.; Ludge, K. Optical feedback induced oscillation bursts in two-state quantum-dot lasers. Opt. Express 2020, 28, 3361–3377. [Google Scholar] [CrossRef]
- Viktorov, E.A.; Mandel, P.; O’Driscoll, I.; Carroll, O.; Huyet, G.; Houlihan, J.; Tanguy, Y. Low-frequency fluctuations in two-state quantum dot lasers. Opt. Lett. 2006, 31, 2302–2304. [Google Scholar] [CrossRef]
- Zhou, Y.G.; Duan, J.N.; Grillot, F.; Wang, C. Optical noise of dual-state lasing quantum dot lasers. IEEE J. Quantum Electron. 2020, 56, 2001207. [Google Scholar] [CrossRef]
- Veselinov, K.; Grillot, F.; Cornet, C.; Even, J.; Bekiarski, A.; Gioannini, M.; Loualiche, S. Analysis of the double laser emission occurring in 1.55-mu m InAs-InP (113) B quantum-dot lasers. IEEE J. Quantum Electron. 2007, 43, 810–816. [Google Scholar] [CrossRef] [Green Version]
- Dehghaninejad, A.; Sheikhey, M.M.; Baghban, H. Dynamic behavior of injection-locked two-state quantum dot lasers. J. Opt. Soc. Am. B 2019, 36, 1518–1524. [Google Scholar] [CrossRef]
- Wang, C.; Grillot, F.; Even, J. Impacts of wetting layer and excited state on the modulation response of quantum-dot lasers. IEEE J. Quantum Electron. 2012, 48, 1144–1150. [Google Scholar] [CrossRef] [Green Version]
- Ohnesorge, B.; Albrecht, M.; Oshinowo, J.; Forchel, A.; Arakawa, Y. Rapid carrier relaxation in self-assembled InxGa1-xAs/GaAs quantum dots. Phys. Rev. B 1996, 54, 11532–11538. [Google Scholar] [CrossRef]
- Ignatiev, I.V.; Kozin, I.E.; Nair, S.V.; Ren, H.W.; Sugou, S.; Masumoto, Y. Carrier relaxation dynamics in InP quantum dots studied by artificial control of nonradiative losses. Phys. Rev. B 2000, 61, 15633–15636. [Google Scholar] [CrossRef] [Green Version]
- Grillot, F.; Wang, C.; Nederi, N.A.; Even, J. Modulation Properties of Self-Injected Quantum-Dot Semiconductor Diode Lasers. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1900812. [Google Scholar] [CrossRef]
- Chen, H.; Lei, T.F.; Lu, S.; Dai, W.P.; Qiu, L.J.; Zhong, L. Dynamics and Complexity Analysis of Fractional-Order Chaotic Systems with Line Equilibrium Based on Adomian Decomposition. Complexity 2020, 2020, 5710765. [Google Scholar] [CrossRef]
- AL-Hosiny, N.M. Effect of linewidth enhancement factor on the stability map of optically injected distributed feedback laser. Opt. Rev. 2014, 21, 261–264. [Google Scholar] [CrossRef]
- Abdulrhmann, S.; Yamada, M.; Ahmed, M. Numerical modeling of the output and operations of semiconductor lasers subject to strong optical feedback and its dependence on the linewidth-enhancement factor. Int. J. Numer. Model. Electron. Netw. Devices Fields 2011, 24, 218–229. [Google Scholar] [CrossRef]



| Symbol | Parameter | Value |
|---|---|---|
| Capture time from WL to ES | 12.6 ps | |
| Capture time from ES to GS | 8 ps | |
| Relaxation time from WL to GS | 15 ps | |
| Escape time from GS to ES | 10.4 ps | |
| Escape time from ES to WL | 5.4 ns | |
| Spontaneous emission time from WL | 0.5 ns | |
| Spontaneous emission time from ES | 0.5 ns | |
| Spontaneous emission time from GS | 1.2 ps | |
| Photon lifetime | 4.1 ps | |
| NB | Total number of QD | 1.0 × 107 |
| Γp | Optical confinement factor | 0.06 |
| nr | Refractive index | 3.5 |
| τin | Round-trip time | 10 ps |
| aGS | Differential gain from GS | 5.0 × 10−15 cm2 |
| aES | Differential gain from ES | 10.0 × 10−15 cm2 |
| ξGS | Gain compression factor from GS | 1.0 × 10−16 cm3 |
| ξES | Gain compression factor from ES | 8.0 × 10−16 cm3 |
| βsp | Spontaneous emission factor | 5.0 × 10−6 |
| ωGS | Angular frequency from GS | 1.446 × 1015 rad/s |
| ωES | Angular frequency from ES | 1.529 × 1015 rad/s |
| VB | Active region volume | 5.0 × 10−11 cm3 |
| VS | Resonant cavity volume | 0.833 × 10−15 cm3 |
| η | Injection efficiency | 0.25 |
| q | Elementary charge | 1.6 × 10−19 C |
| τ | Feedback delay time | 100 ps |
| α | Linewidth enhancement factor | 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.-H.; Wu, Z.-M.; Jiang, Z.-F.; Xia, G.-Q. Nonlinear Dynamics of Two-State Quantum Dot Lasers under Optical Feedback. Photonics 2021, 8, 300. https://doi.org/10.3390/photonics8080300
Wang X-H, Wu Z-M, Jiang Z-F, Xia G-Q. Nonlinear Dynamics of Two-State Quantum Dot Lasers under Optical Feedback. Photonics. 2021; 8(8):300. https://doi.org/10.3390/photonics8080300
Chicago/Turabian StyleWang, Xiang-Hui, Zheng-Mao Wu, Zai-Fu Jiang, and Guang-Qiong Xia. 2021. "Nonlinear Dynamics of Two-State Quantum Dot Lasers under Optical Feedback" Photonics 8, no. 8: 300. https://doi.org/10.3390/photonics8080300
APA StyleWang, X.-H., Wu, Z.-M., Jiang, Z.-F., & Xia, G.-Q. (2021). Nonlinear Dynamics of Two-State Quantum Dot Lasers under Optical Feedback. Photonics, 8(8), 300. https://doi.org/10.3390/photonics8080300





