Efficient Fourier Single-Pixel Imaging with Gaussian Random Sampling
Abstract
:1. Introduction
2. Principle
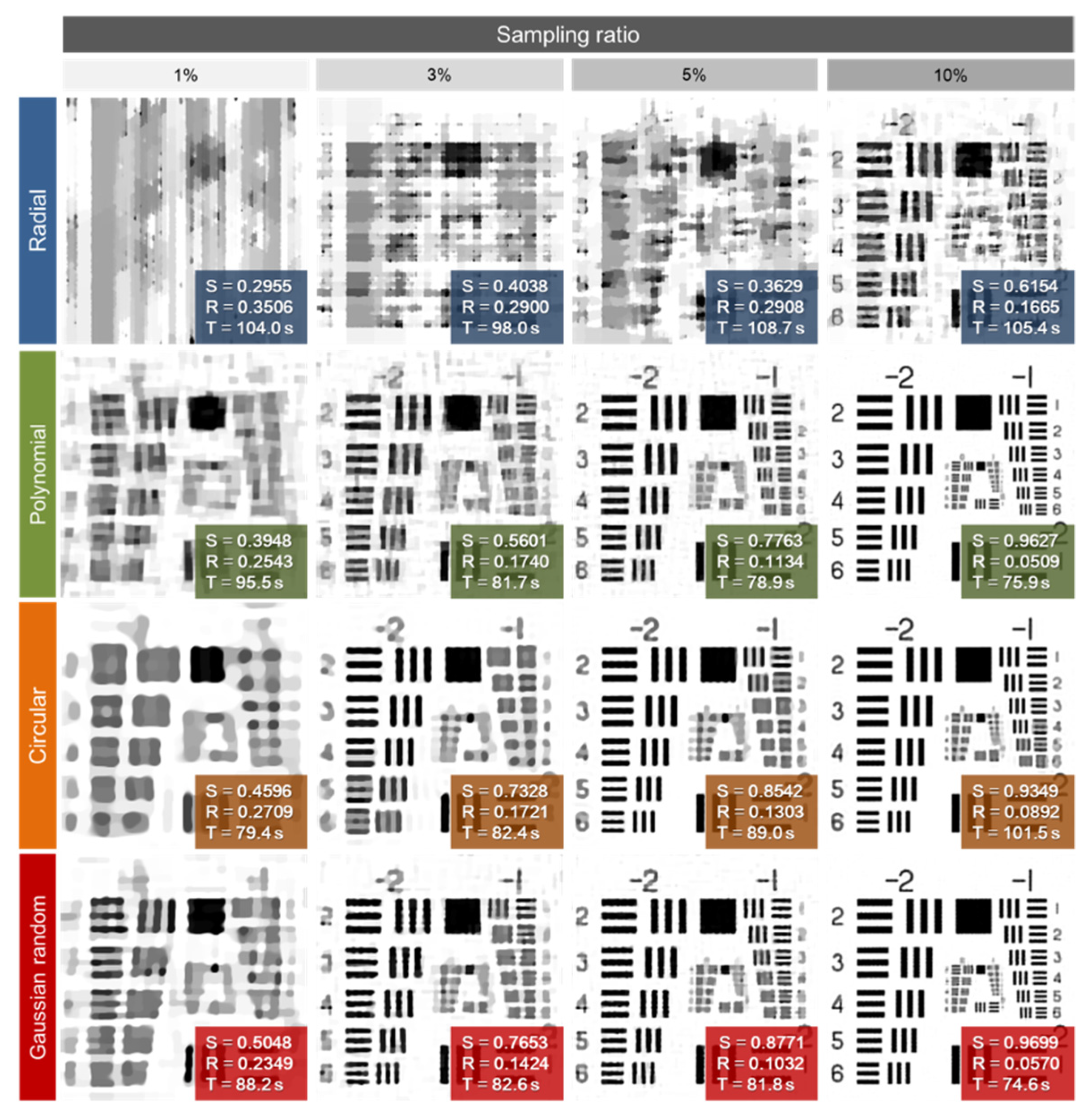
3. Simulation
4. Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Decker, J.A. Hadamard-Transform Image Scanning. Appl. Opt. 1970, 9, 1392–1395. [Google Scholar] [CrossRef]
- Edgar, M.; Gibson, G.; Padgett, M. Principles and prospects for single-pixel imaging. Nat. Photonics 2019, 13, 13–20. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, J. Single-pixel imaging and its application in three-dimensional reconstruction: A brief review. Sensors 2019, 19, 732. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gibson, G.; Johnson, S.; Padgett, M. Single-pixel imaging 12 years on: A review. Opt. Express 2020, 28, 28190–28208. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.J.; Edgar, M.P.; Gibson, G.M.; Sun, B.Q.; Radwell, N.; Lamb, R.; Padgett, M.J. Single-pixel three-dimensional imaging with time-based depth resolution. Nat. Commun. 2016, 7, 12010. [Google Scholar] [CrossRef] [PubMed]
- Phillips, D.B.; Sun, M.J.; Taylor, J.M.; Edgar, M.P.; Barnett, S.M.; Gibson, G.M.; Padgett, M.J. Adaptive foveated single-pixel imaging with dynamic supersampling. Sci. Adv. 2017, 3, e1601782. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.J.; Edgar, M.P.; Phillips, D.B.; Gibson, G.M.; Padgett, M.J. Improving the signal-to-noise ratio of single-pixel imaging using digital microscanning. Opt. Express 2016, 24, 10476–10485. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.H.; Chen, W.; Penuelas, J.; Padgett, M.; Sun, M.J. 1000 fps computational ghost imaging using LED-based structured illumination. Opt. Express 2018, 26, 2427–2434. [Google Scholar] [CrossRef] [Green Version]
- Greenberg, J.; Krishnamurthy, K.; Brady, D. Compressive single-pixel snapshot x-ray diffraction imaging. Opt. Lett. 2014, 39, 111–114. [Google Scholar] [CrossRef]
- Yu, H.; Lu, R.; Han, S.; Xie, H.; Du, G.; Xiao, T.; Zhu, D. Fourier-transform ghost imaging with hard X rays. Phys. Rev. Lett. 2016, 117, 113901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, A.; He, Y.; Wu, L.; Chen, L.; Wang, B. Tabletop x-ray ghost imaging with ultra-low radiation. Optica 2018, 5, 374–377. [Google Scholar] [CrossRef] [Green Version]
- Chan, W.; Charan, K.; Takhar, D.; Kelly, K.; Baraniuk, R.; Mittleman, D. A single-pixel terahertz imaging system based on compressed sensing. Appl. Phys. Lett. 2008, 93, 121105. [Google Scholar] [CrossRef] [Green Version]
- Shrekenhamer, D.; Watts, C.; Padilla, W. Terahertz single pixel imaging with an optically controlled dynamic spatial light modulator. Opt. Express 2013, 21, 12507–12518. [Google Scholar] [CrossRef]
- Hornett, S.; Stantchev, R.; Vardaki, M.; Beckerleg, C.; Hendry, E. Subwavelength terahertz imaging of graphene photoconductivity. Nano Lett. 2016, 16, 7019–7024. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Liu, X.; Yao, X.; Wang, C.; Zhai, Y.; Zhai, G. Complementary compressive imaging for the telescopic system. Sci. Rep. 2015, 4, 5834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Studer, V.; Bobin, J.; Chahid, M.; Mousavi, H.; Candes, E.; Dahan, M. Compressive fluorescence microscopy for biological and hyperspectral imaging. Proc. Natl. Acad. Sci. USA 2012, 109, E1679–E1687. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Ma, X.; Zhong, J. Single-pixel imaging by means of Fourier spectrum acquisition. Nat. Commun. 2015, 6, 6225. [Google Scholar] [CrossRef] [Green Version]
- Bian, L.; Suo, J.; Hu, X.; Chen, F.; Dai, Q. Efficient single pixel imaging in Fourier space. J. Opt.-UK 2016, 18, 085704. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Zhu, S.; Zhao, H.; Xu, B.; Li, X. Adaptive regional single-pixel imaging based on the Fourier slice theorem. Opt. Express 2017, 25, 15118–15130. [Google Scholar] [CrossRef]
- Huang, J.; Shi, D.; Yuan, K.; Hu, S.; Wang, Y. Computational-weighted Fourier single-pixel imaging via binary illumination. Opt. Express 2018, 26, 16547–16559. [Google Scholar] [CrossRef]
- Xu, B.; Jiang, H.; Zhao, H.; Li, X.; Zhu, S. Projector-defocusing rectification for Fourier single-pixel imaging. Opt. Express 2018, 26, 5005–5017. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.; Peng, J.; Yao, M.; Zheng, G.; Zhong, J. Simultaneous spatial, spectral, and 3D compressive imaging via efficient Fourier single-pixel measurements. Optica 2018, 5, 315–319. [Google Scholar] [CrossRef]
- Sun, M.; Meng, L.; Edgar, M.; Padgett, M.; Radwell, N. A Russian dolls ordering of the Hadamard basis for compressive single-pixel imaging. Sci. Rep. 2017, 7, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Yu, W. Super sub-Nyquist single-pixel imaging by means of cake-cutting Hadamard basis sort. Sensors 2019, 19, 4122. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Liu, Y. Single-pixel imaging with origami pattern construction. Sensors 2019, 19, 5135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, X.; Stantchev, R.; Yang, F.; Pickwell-MacPherson, E. Super sub-Nyquist single-pixel imaging by total variation ascending ordering of the Hadamard basis. Sci. Rep. 2020, 10, 9338. [Google Scholar] [CrossRef]
- Vaz, P.; Amaral, D.; Requicha Ferreira, L.; Morgado, M.; Cardoso, J. Image quality of compressive single-pixel imaging using different Hadamard orderings. Opt. Express 2020, 28, 11666–11681. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Yang, Z.; Liu, X.; Wu, L. Coloured computational imaging with single-pixel detectors based on a 2D discrete cosine transform. J. Mod. Opt. 2017, 64, 259–264. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wang, X.; Zheng, G.; Zhong, J. Fast Fourier single-pixel imaging via binary illumination. Sci. Rep. 2017, 7, 12029. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Gong, L.; Xu, X.; Hai, P.; Shen, Y.; Suzuki, Y.; Wang, L. Motionless volumetric photoacoustic microscopy with spatially invariant resolution. Nat. Commun. 2017, 8, 780. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Zheng, G.; Zhong, J. Hadamard single-pixel imaging versus Fourier single-pixel imaging. Opt. Express 2017, 25, 19619–19639. [Google Scholar] [CrossRef] [PubMed]
- Meng, W.; Shi, D.; Huang, J.; Yuan, K.; Wang, Y.; Fan, C. Sparse Fourier single-pixel imaging. Opt. Express 2019, 7, 31490–31503. [Google Scholar]
- Floyd, R.; Steinberg, L. An adaptive algorithm for spatial grey. Proc. Soc. Inf. Disp. 1976, 17, 75–77. [Google Scholar]
- Agustsson, E.; Timofte, R. NTIRE 2017 Challenge on Single Image Super-Resolution: Dataset and Study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 126–135. [Google Scholar]
- Candès, E.; Romberg, J. l1-magic: Recovery of Sparse Signals via Convex Programming. Available online: https://statweb.stanford.edu/~candes/software/l1magic/downloads/l1magic.pdf (accessed on 1 June 2021).
- Candès, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inform. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2014, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Jiang, P.; Jiang, M.; Xu, L.; Wu, L.; Yang, X.; Zhang, W.; Zhang, J.; Zhang, Y. High imaging quality of Fourier single pixel imaging based on generative adversarial networks at low sampling rate. Opt. Lasers Eng. 2021, 140, 106533. [Google Scholar] [CrossRef]
- Higham, C.; Murray-Smith, R.; Padgett, M.; Edgar, M. Deep learning for real-time single-pixel video. Sci. Rep. 2018, 8, 2369. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Li, X.; Peng, X.; Sun, B. Imaging high-speed moving targets with a single-pixel detector. Opt. Express 2020, 28, 7889–7897. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Zhao, M.; Tian, Z.; Willomitzer, F.; Cossairt, O. Compressive ghost imaging through scattering media with deep learning. Opt. Express 2020, 28, 17395–17408. [Google Scholar] [CrossRef] [PubMed]
- Rizvi, S.; Cao, J.; Hao, Q. Deep learning based projector defocus compensation in single-pixel imaging. Opt. Express 2020, 28, 25134–25148. [Google Scholar] [CrossRef]
- Rizvi, S.; Cao, J.; Zhang, K.; Hao, Q. DeepGhost: Real-time computational ghost imaging via deep learning. Sci. Rep. 2020, 10, 11400. [Google Scholar] [CrossRef] [PubMed]
- Rizvi, S.; Cao, J.; Zhang, K.; Hao, Q. Improving imaging quality of real-time Fourier single-pixel imaging via deep learning. Sensors 2019, 19, 4190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radwell, N.; Johnson, S.; Edgar, M.; Higham, C.; Murray-Smith, R.; Padgett, M. Deep learning optimized single-pixel LiDAR. Appl. Phys. Lett. 2019, 115, 231101. [Google Scholar] [CrossRef] [Green Version]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Z.; Guo, X.; Lu, T.; Qi, P.; Zhang, Z.; Zhong, J. Efficient Fourier Single-Pixel Imaging with Gaussian Random Sampling. Photonics 2021, 8, 319. https://doi.org/10.3390/photonics8080319
Qiu Z, Guo X, Lu T, Qi P, Zhang Z, Zhong J. Efficient Fourier Single-Pixel Imaging with Gaussian Random Sampling. Photonics. 2021; 8(8):319. https://doi.org/10.3390/photonics8080319
Chicago/Turabian StyleQiu, Ziheng, Xinyi Guo, Tian’ao Lu, Pan Qi, Zibang Zhang, and Jingang Zhong. 2021. "Efficient Fourier Single-Pixel Imaging with Gaussian Random Sampling" Photonics 8, no. 8: 319. https://doi.org/10.3390/photonics8080319
APA StyleQiu, Z., Guo, X., Lu, T., Qi, P., Zhang, Z., & Zhong, J. (2021). Efficient Fourier Single-Pixel Imaging with Gaussian Random Sampling. Photonics, 8(8), 319. https://doi.org/10.3390/photonics8080319




