Spatiotemporal Evolutions of Similariton Pulses in Multimode Fibers with Raman Amplification

Abstract

This paper aims to pave the way towards the demonstration of spatiotemporal similariton pulses’ evolution in passive multimode fibers with Raman amplification. We numerically present this issue in graded-index and step-index multimode fibers and provide a first look at the complex spatiotemporal dynamics of similariton pulses. The results showed that the similariton pulses could be generated in both multimode fibers. The temporal and spectral evolution of the pulses can be characterized as parabolic shapes with linear chirp and kW peak power. By compressing these, high-energy femtoseconds pulses can be obtained, starting initial picosecond pulses. A spatial beam profile could be preserved in both multimode fibers with the most energy coupled to the fundamental mode. Specifically, the similariton pulses’ generation with Raman amplification in a graded-index multimode fiber improves the spatial beam self-cleaning process under the different initial modes’ excitation. The observation of a new beam self-cleaning process is another attractor feature of propagation in graded-index multimode fibers.

1. Introduction

In recent years, there has been increased interest in nonlinear wave propagation in multimode optical fibers (MM-Fibers). The traditional view of MM-Fibers as undesirable for nonlinear applications is gradually changing since MM-Fibers support a variety of new spatiotemporal phenomena, such as multimode solitons, supercontinuum generation, the multiple filamentation process, and wave condensation [1]. The formation of multimode solitons is limited by different group delays associated with different propagating modes and nonlinear coupling terms, as was reported by early workers [2]. On the other hand, graded-index multimode fibers (GRIN-Fs) reduce the complexity due to the self-imaging effect resulting from the equal spacing of the modal wave with low intermodal dispersion. The theory of multimode light propagation in GRIN-Fs was established in the early 1970s [3]; very recently, the studies of the complex nonlinear spatiotemporal effects in these MM-Fibers have been investigated [4]. Spatiotemporal optical solitons [5], supercontinuum generation [6], spatiotemporal instability [7], and self-similar fiber lasers [8] are already reported. The above-mentioned numerical studies and experimental observations are remarkable examples showing the complex nonlinear pulse dynamics in MM-Fibers. Motivated by these works and the others, one may thus naturally wonder whether similariton pulses may also occur in MM-Fibers.

Similariton pulses are shape-preserving waves that appear due to the interaction of nonlinearity, normal dispersion, and gain in optical fibers. This causes the shape of an arbitrary input pulse to converge to a parabolic pulse shape and evolves in a self-similar manner. Temporal similaritons have been studied extensively in the context of single-mode optical fibers (SMFs) with different amplification processes (Raman, Erbium, and Ytterbium amplification) [9,10,11,12]. These studies have already demonstrated the interesting properties of amplifiers’ similaritons pulses in conventional SMFs. The platform based on MM-Fibers could be a good candidate for the amplification process as well and the question of whether spatiotemporal similariton pulses could be formed inside the MM-Fibers.

In this paper, we propose a new configuration to demonstrate the existence of the spatiotemporal similariton pulses in two different passive MM-Fiber types (GRIN-F and Step-Index Fiber (STEP-F)) with Raman amplification. For our numerical studies, we used the generalized multimode nonlinear Schrödinger equation (GMMNLSE) considering the interaction of nonlinearity, normal dispersions, gain, and modal interactions represented by mode coupling. The gain is generated by Raman amplification owing to their advantages. It may occur at any passive fiber type and exists at any wavelength as long as an appropriate pump laser is available. The results showed that the characteristics of the similariton pulses generated in both MM-Fibers present similar behavior, as obtained in SMFs with the most energy coupled to the fundamental mode. High energy similariton pulses have temporal and spectral parabolic shapes with a linear chirp. The pulses generated in both cases can also be compressible down to a femtosecond pulse duration with ~100 kW of peak power. However, the spatiotemporal dynamics, as well as the spatial beam profiles under different initial modes’ excitation in both MM-Fibers, are very different. A new type of beam self-cleaning process based on similariton pulse generation with Raman amplification in GRIN-F could be observed.

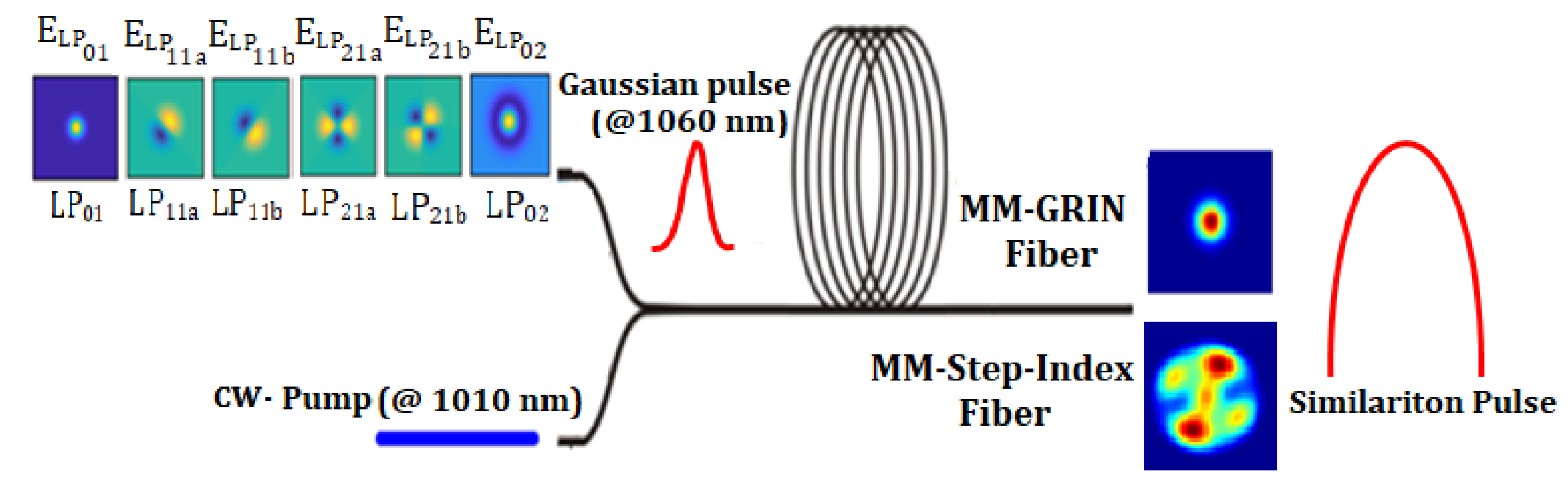
2. Numerical Setup and Results

To investigate the spatiotemporal evolutions of similariton pulses in MM-Fibers with Raman amplification, we used the platform presented in Figure 1. The MM-Fibers used in our numerical studies have parabolic and step refractive index profiles in the GRIN-F and the STEP-F with an identical core radius of 25 µm and an index contrast of Δ = 0.0068, where NA = 0.17, respectively. To reduce the computational time, we considered the first six linearly polarized modes (LP_mn), as shown in Figure 1.

We calculated the dispersions, the nonlinear, and the coupling coefficients using codes introduced by Wright et al. [13]. The MM-Fibers characterized by the dispersions coefficients β₂ for the six modes are as follows: 16.76 ps²/km (LP₀₁), 16.75 ps²/km (LP_11a and LP_11b), and 16.74 ps²/km (LP_21a, LP_21b, and LP₀₂) for the GRIN-F and 16.49 ps²/km (LP₀₁), 16.06 ps²/km (LP_11a and LP_11b), 15.50 ps²/km (LP_21a and LP_21b), and 15.31 ps²/km (LP₀₂) for the STEP-F at 1060 nm. The effective areas, A_eff, and the nonlinear coefficients, γ, of the GRIN-F and the STEP-F are 155.09 μm² and 1.22 W⁻¹ km⁻¹, and 966.43 μm² and 0.2 W⁻¹ km⁻¹, respectively. As the effective area of the fundamental mode in the MM-Fibers is scaled as the core radius, the effective nonlinearity of the MM-Fibers is comparable with SMFs [4]. These features make both MM-Fibers suitable for Raman amplification.

Numerical simulations for the spatiotemporal nonlinear dynamics of similariton pulses are conducted using the GMMNLSE [14] and solved using the split-step Fourier method [15]. The GMM-NLSE (1) is including the effects of stimulated Raman scattering, higher-order dispersion, self-steepening, and intermodal effects.

$$\begin{gathered} {\partial }_z{A}_p=i\left({\beta }_0^{\left(p\right)}-\Re \left[{\beta }_0^{\left(0\right)}\right]\right)A_p-\left({\beta }_1^{\left(p\right)}-\Re \left[{\beta }_1^{\left(0\right)}\right]\right)\frac{\partial A_P}{\partial t}+i{{\displaystyle \sum }}_{n\ge 2}\frac{{\beta }_n^{\left(p\right)}}{n!}{\left(i\frac{\partial }{\partial t}\right)}^n{A}_p+ \\ i\frac{n_{2{\omega }_0}}{c}\left(1+\frac{i}{{\omega }_0}\partial t\right){{\displaystyle \sum }}_{l,m,n}\left\{\left(1-f_R\right)S_{plmn}^k{A}_l{A}_m{A}_n^{*}+f_R{A}_l{S}_{plmn}^R{{\displaystyle \int }}_{-\infty }^{t}d\tau A_m\left(z,t-\tau \right)A_n^{*}\left(z,t-\tau \right)h_R\left(\tau \right)\right\} \end{gathered}$$

(1)

where Ap(z,t) is the electric field temporal envelope for spatial mode p; and the first, the second, and the third term on the right-hand side indicate the propagation constant mismatch responsible for multimode interference or mode beating, the modal dispersion or modal walk-off and the higher-order dispersion coefficients, respectively. In the fourth term, n₂ represents the nonlinear refractive index (n₂ = 3.2 × 10⁻²⁰ m²W⁻¹), f_R is the fractional contribution of the Raman effect (f_R = 0.18), $S_{plmn}^k$ and $S_{plmn}^R$ represent the nonlinear coupling coefficients for the Raman and Kerr effect, respectively, h_R is the delayed Raman response function, and shock terms are neglected.

The gain can be added into the GMMNLSE by an additional term, g_pA_p, where g_p is the small-signal gain for the electric field in mode p. For short pulses, g_p is defined as g_p = g₀/(1 + E_p/E_sat), where g₀ is the initial gain, E_p is the energy of mode p, and E_sat is the saturation energy. E_sat, for both MM-Fibers, is estimated to be about 1.2 nJ. In our numerical studies, we selected the CW-pump source operating at 1010 nm for Raman gain. A Gaussian-shaped input pulse operating at 1060 nm with a pulse duration of 2 ps, pulse energy of 0.4 nJ, peak power of 200 W, and spectral bandwidth of 0.8 nm is used. The shift of 13.2 THz (corresponding to 50 nm) between the pump and the signal is selected for optimum Raman gain in the silica fibers. The fiber length of 130 m is chosen to ensure sufficient Raman gain.

In MM-Fibers with gain, the different modes receive gain and usually compete since they overlap with the same gain medium. In our case, the competition between the pump and signal modes could not be considered due to the CW-pump used for Raman gain. The Raman gain for each mode is defined as G_{p (dB)} = exp (g_R P₀ L_eff/A_eff) [16], where L_eff is the effective fiber length, P₀ is the CW-pump power, and g_R is the Raman gain coefficient at the CW-pump wavelength. Note that the modal gain can be controlled by the effective area of modes, A_eff, and the Raman gain coefficient (considering the CW-pump power is fixed). Consequently, the variation of the Raman gain for each spatial mode as a function of the proposed MM-Fiber’s length is evaluated in Figure 2a,b for the GRIN-F and the STEP-F, respectively, considering the overfilling nature of the CW-pump and the power is 100 W. We also calculated on the two plots in Figure 2c, the effective area of modes in the proposed MM-Fibers confirm that the effective area of modes in the STEP-F is larger than in the GRIN-F of the same radius [14].

From Figure 2a,b, we note that the distribution of gain inside both MM-Fibers is different due to the difference in the structures and the mechanism of the propagations between them. In the GRIN-F, the fundamental mode, LP₀₁, received the largest gain compared to the higher-order modes (HOMs). Primarily, because the LP₀₁ mode is more confined in the higher gain region, since the relatively high GeO₂ dopants in the center of the GRIN-F core result in a higher peak Raman gain coefficient. The peak value of the Raman gain coefficient is estimated as g_R = 7 × 10⁻¹³ m/W (at a 1060-nanometer wavelength and considering the GeO2 doping). Second, since the modal gain is inversely proportional to the effective modal area, the latter being higher for the LP₀₁ mode with the smaller effective area, as shown in Figure 2c (upper figure). The overlap between other HOMs and the pump results in a smaller gain. The modal gain at the fiber length of 130 m is equal to 20, 2, 1.5, and 0.5 dB for the LP₀₁, LP_11a−b, LP_21a−ba, and LP₀₂ mode, respectively. In the case of STEP-F, the different modes could receive the same gain since the Raman gain is flat and uniformly distributed along with the STEP-F core. Note, however, that the LP₀₁ and LP₀₂ modes have the larger and the smaller effective areas (Figure 2c), respectively, confirming that the effective area of the LP_0n modes decreases with the mode order in the STEP-F [13]. The effective areas of the other modes, LP_11a, LP_11b, LP_21a, and LP_21b, are nearly equal. As a result, the overlap between the CW-pump and all the modes under consideration leads to modal gain variations, as shown in Figure 2b. The gain of the LP₀₁ mode is equal to 20 dB and that of the LP₀₂ mode is 25 dB, where the gain of LP_11a-b and LP_21a-b is 21.3 and 21.5 dB, respectively.

To study the dynamics of similariton pulses in both MM-Fibers, and to present their characteristics and behaviors compared to those generated in SMFs, we first started by exciting only the fundamental mode, LP₀₁. We assume the Gaussian-shaped input pulse with a pulse duration of 2 ps and energy of 0.4 nJ propagates through 130 m of the proposed MM-Fibers and under the Raman amplification effect. We set the pulse energy, mostly coupled in the LP₀₁ mode, as 99%. We consider the weak excitation of the other modes, which could be the case in an experiment. The temporal and the spectral forms of all the modes at the MM-Fibers’ output can be obtained, as shown in Figure 3a–e, which is presented in uniform and normalized scales. These results show that only the LP₀₁ mode evolves towards a parabolic form and, subsequently, develops a wide temporal and spectral expansion. As expected for all the other modes, only the LP₀₁ mode is strongly amplified and its energy increased exponentially with the fiber length to reach a value of 37.8 nJ, as shown in Figure 3c,f, which validates the amplifier similariton pulse formation of the LP₀₁ mode, while the other HOMs did not converge to the similariton pulses. As the similaritons depend only on the pulse energy and on the gain of the amplifier, the most initial pulse energy coupling into the LP₀₁ mode results in a higher nonlinearity compared with the other HOMs. Therefore, even with the same amount of gain distributed among all the modes, as in the case of the STEP-F, only the LP₀₁ mode transforms into the parabolic shape and gains energy. The other HOMs did not transform into the parabolic shape and then lost their energy, which is also the result of the inadequate nonlinear phase accumulation. It can be understood as follows: The interplay of nonlinearity, normal dispersion, and gain is important for reshaping and maintaining the parabolic pulse shape during propagation in the fiber.

It should be noticed that the energy exchange is observed between the HOMs in the GRIN-F (Figure 3a,b) because the intermodal group delays are smaller inside this type of fiber. However, the energy level of HOMs (0.072 nJ) is extremely low compared with that of the LP₀₁ mode and, thus, any perturbation on the similariton pulse evolution did not occur during its propagation in the GRIN-F. On the other hand, the energy coupling to the HOMs is not observed in the STEP-F (Figure 3d,e) and each of them evolve as in a single-mode case.

Figure 4 shows the formation of the similariton pulses of the LP₀₁ mode in temporal and spectral domains inside the proposed MM-Fibers. Figure 4a,c are highlighting the reshaping of the pulse during its propagation inside the GRIN-F, followed by its self-similar evolution that appeared according to two parts of separate regimes. The first part is corresponding to the restructuring and the reshaping of the LP₀₁ mode and the appearance of characteristics of the parabolic pulse profile. A typical parabolic shape is obtained at 30 m of pulse propagation inside the GRIN-F, which is defined as the characteristic length Z_c = (3/2g₀) ln (Ng₀/6γP_c) [10], calculated for N~100. In the second part, beyond Z_C, the LP₀₁ mode has the characteristics of similariton and evolves in a self-similar manner with an increase in its wide temporal and spectral expansion. We note the absence of any pulse deformation or oscillation caused by wave breaking, and modulation instability sidebands did not occur in the generated spectrum. At the output of the GRIN-F, the input Gaussian pulse is now transformed into a parabolic shape with a linear chirp (Figure 4d). The pulse duration is 32 ps and the pulse energy is about 37.8 nJ. The spectrum generated by the self-similar amplification regime also has a parabolic form (Figure 4b) with a bandwidth of 16 nm. The small ripples seen in the middle of the spectrum are the result of the limited bandwidth by the finite spectral bandwidth of Raman gain (about 23 nm according to [17]). At the same time, Figure 4e–h show the self-similar regime and similariton formation for 130 m of pulse propagation inside the STEP-F, although the mechanism of the propagations is different. Specifically, the time duration and the energy of the output pulse are 15.5 ps and 37.8 nJ, respectively (Figure 4h). Here, the input pulse has evolved as a parabolic shape beyond 55 m of propagation, which is just a transient state of the pulse evolution in the fiber and under amplification (Figure 4e,g). The ratio between the nonlinearity coefficient (γ) and the dispersion (β₂) is high in the GRIN-F compared to that in the STEP-F. Therefore, we observed that the input pulse converges to a parabolic shape rapidly in the GRIN-F (30 m) than in the STEP-F (55 m). Likewise, the decrease in the nonlinearity coefficient caused less spectral broadening (about 9 nm) for the STEP-F (Figure 4f). The above results imply that the output pulses have a parabolic pulse shape with a linear chirp and a high-energy amplification. These pulses generated in the GRIN-F and the STEP-F can be compressed down to 255 and 340 fs, respectively (inset Figure 4d,h). The compressed pulses’ peak power is ~100 KW and that, when compared to the original input pulse (pulse duration of 2 ps and peak power of 200 W), represents a factor of ~8 and ~6 temporal compressions, and an amplification factor of 500 could be achieved in both cases. It should be noted here that the pedestals on the compressed pulses are being observed. However, their energy is extremely low compared to that of the main lobes. We have estimated 70 and 90% of the total energy is contained in the main lobes of the compressed pulses, while 30 and 10% is in the pedestals by comparing the energies of the similariton pulses (37.8 nJ) with those of the compressed pulses (25.5 and 34 nJ), in the case of the GRIN-F and the STEP-F, respectively. We can mention that the pedestals could be observed as the features of the other HOMs. Thus, the pedestals on the compressed pulses are more relevant in the case of the GRIN-F, because the walk-off of the modes is smaller inside this type of fiber (Figure 3a,b), and thereby the generated temporal profile of the compressed pulse is more affected by the presence of the other HOMs.

The output spatial profiles of the total field containing all the modes during the pulse propagation inside the GRIN-F and the STEP-F are presented in the inset of Figure 3c,f. The excitation of the LP₀₁ mode with the most energy results in the Gaussian intensity distributions being preserved along the both MM-Fibers. Due to the different mode field diameter behavior of the LP₀₁ mode for both MM-Fibers, we also observed the different beam sizes.

Later we consider the effect of different launch conditions on the spatiotemporal pulse evolution. In this part, the simulations are performed to investigate the effect of the initial input energy distribution between the modes. To create a significant change, we consider the first six modes with equal initial energy distributions (total peak power of 200 W among all the modes). Indeed, such a configuration can be achieved using a spatial light modulator (SLM) [18]. We considered the same GRIN–F and STEP–F parameters. For a propagation length of 130 m, we noticed that the initial pulse is converged to a similariton pulse in the GRIN-F for the LP₀₁ mode only, and it is significantly amplified compared to the HOMs, as shown in Figure 5a–c. While the HOMs did not gain energy, even they have the same amount of initial energy. It can be explained that the similariton pulse formation in the GRIN-F significantly depends on the Raman gain of modes, which favors the LP₀₁ mode since it is received the largest gain compared to HOMs (Figure 2a). On the other hand, in the STEP-F, the pulse is broken up into sub-pulses, presented by different modes, whose separation grows linearly with the fiber length owing to the large walk-off between modes, because the modes have rather different group velocities, and each of them travels with their group velocity as in a single-mode case. Therefore, all the modes evolved towards the respective similariton forms, and they are amplified with a different modal gain coefficient (Figure 5d–f). The greater walk-off of the modes in the STEP-F means that the coupling between HOMs may be less efficient. However, when the energy of the modes increased during the similaritons’ formation process, the coupling between the degenerate modes, which travel at the same group velocity, seems very relevant in the case of LP_21a and LP_21b, as shown in Figure 5f, in which the energy oscillations between this pair of modes is observed.

We also simulated the spatial profiles’ evolution of the total field containing all the modes equally exciting inside the GRIN-F and the STEP-F. Due to the similariton pulse generation that occurred only on the LP₀₁ mode, an initial spatial beam profile, even composed by the LP₀₁ and HOMs, is progressively cleaned to a centered beam profile beyond 50 m of propagation, as shown in Figure 6a. The centered beam has Gaussian-like intensity distributions of the fundamental mode called a bell-shape beam [19]. On the other hand, the spatial beam evolution in the STEP-F presented in Figure 6b shows that the spatial profile containing all the modes did not converge to a Gaussian-like intensity distribution in this case, and the spatial energy transfer between pairs of modes LP_21a and LP_21b are visible. As a result, the spatiotemporal nonlinear dynamics and the output spatial beam profiles are very different. The similariton generation with Raman amplification in the GRIN-F occurred only on the LP₀₁, improving the spatial beam self-cleaning and using very low energetic input pulses, unlike the cases using the stimulated Raman scattering (SRS) effect [20]. It is important to underline that the beam self-cleaning reported in this work is fundamentally different from that observed in [20], which is induced via the SRS process in MM-Fibers. The signal used to be strong enough to induce a Raman conversion, and the cleaned beam appears at the Stokes’ wavelength. The modal gain competition between the Stokes’ modes is considered, where only red-shift wavelengths have been carried by the LP₀₁ mode. In contrast, here, the beam self-cleaning appears without any wavelength conversion. The modal gain competition and the walk-off between pump and signal could not be considered due to the strong CW-pump used for Raman gain. In addition, the initial pulse energy used in this work (0.4 nJ) is not strong enough to generate mode stokes for the SRS process.

3. Discussions

The present study reveals that the spatiotemporal similariton pulse evolutions in MM-Fibers with the Raman amplification process and its new fundamental spatiotemporal nonlinear dynamics is an open question for investigation. Several aspects of spatiotemporal similariton pulse evolution were studied, such as whether spatiotemporal similariton in different kinds of MM-Fibers (GRIN-F and STEP-F) can exist, how they propagate under various initial conditions, and the impact of the multimode propagation regime on its spatial behavior. We first started with the case where most of the initial energy (0.4 nJ) is coupled on the fundamental LP₀₁ mode. In that case, the energy transfer from the LP₀₁ mode into the other HOMs is limited, and the other HOMs being decoupled since the coupling effect is mainly limited to energy-dependent effects [14], and thereby, the MM-Fibers behave as single-mode fibers and observe an attraction towards similariton pulses presented by the LP₀₁ mode only. The other HOMs did not converge to the similariton pulses with a very low initial energy; even they have nearly the same amount of gain in the STEP-F. The LP₀₁ mode evolved into a linearly chirped pulse with a parabolic intensity shape, and its energy is significantly increased to 37.8 nJ after 130 m of propagation in both MM-Fibers with Raman amplification. The similariton pulse duration (FWHM) and spectral bandwidth are 32 ps and 16 nm, respectively in the case of the GRIN-F, and 15.5 ps and 8 nm in the case of the STEP-F, respectively. These results allow for efficient pulse compression since the similariton experienced spectral broadening and high pulse energies. The resulting linear chirp makes it relatively easy to obtain high peak power pulses after compression in a subsequent dispersive optical element. The original input pulses after shaping into similaritons are then compressed using an anomalous dispersion fiber. After a certain propagation distance, a strongly compressed pulse can be obtained. The similariton pulses are compressed to 255 and 340 fs; a factor of ~8 and ~6 temporal compressions are achieved in the case of the GRIN-F and the STEP-F, respectively. The compressed pulses peak power is ~100 KW, and an amplification factor of 500 could be achieved in both cases.

Our second attention is notably in the spatiotemporal behavior of similariton pulses under the condition of the equal energy distributed among all the modes. In that case, the results were different between the GRIN-F and the STEP-F. The main reason is that the distribution of the gain inside each MM-Fiber is different. In the case of the GRIN-F, the Raman gain is higher in the center of the GRIN-F core due to the relatively high GeO₂ content and high nonlinearity. Therefore, the LP₀₁ mode has a larger gain and is strongly amplified compared to HOMs due to its greater overlap with the higher gain. As a result, only the LP₀₁ mode transformed to a similariton pulse and it became dominant. The energy exchange is observed between the HOMs because the walk-off of the modes, which is calculated by $∆{\beta }_1^{\left(p\right)}$ of modes 2–6, is smaller (0.013 ps/m) inside this type of fiber. However, the energy of HOMs is too weak and does not affect the similariton formation process. Moreover, an efficient spatial conversion of a multimode (speckled pattern) beam into a single-mode beam of near-Gaussian shape (bell-shape beam), resembling that of the LP₀₁ mode, which results in beam quality enhancement (called beam clean-up), occurred. The beam clean-up is accompanied by similariton pulses at an output energy of 5.5 nJ that results in a brightness enhancement for the Raman amplification based on GRIN-F, while in the STEP-F, because the gain is nearly flat and distributed uniformly in the core of the fiber, all the modes transformed to the similariton forms, and the spatial beam clean-up does not occur. The modal walk-off ($∆{\beta }_1^{\left(p\right)}$ of modes 2–6 are 0.38, 0.38, 0.89, 0.89, and 1.07 ps/m, respectively) leads the modes to separate temporally, and spatial energy oscillations between the degenerate modes.

We can note the significance of these results by the fact that the similariton generation with Raman amplification in the GRIN-F occurred only on the LP₀₁, improving the spatial beam self-cleaning and using very low energetic input pulses, unlike cases that used rare Yb-doped MM-Fibers, where spatial beam self-cleaning has also been reported, even in the case of a non-parabolic refractive-index profile [19]. In addition, the usage of tapered Yb-doped GRIN-F [21] also enhances the nonlinear effect and improves the spatial Kerr self-cleaning and the decrease in the core-diameter accelerating self-image, and therefore, the nonlinear interaction between the modes is accelerated when injecting a beam into the large core side. However, the power threshold for self-induced spatial cleaning via the Kerr beam self-cleaning is increased (500 W and more), and the amount of power transferred to the cleaning mode is reduced. Note also that Kerr beam self-cleaning may be accompanied by a complex temporal pulse break-up and significant temporal reshaping, as well as a shortening of the input pulses [22].

In summary, we have introduced new results for the control of nonlinear beam reshaping in the spatial, temporal, and spectral domains. Combining similariton pulse and beam self-cleaning in GRIN-F permits obtaining not only high brightness but also high beam quality pulses.

We anticipate that our results will be of general fundamental interest because they provide the first example of spatiotemporal similariton generation in MM-Fibers with Raman amplification. We can furthermore expect a particular interest in the development of higher pulse energy and short-pulse sources for high-power spatiotemporal multimode fiber lasers [23]. MM-Fibers allow for a considerably higher pulse energy than single-mode fibers and spatiotemporal similariton may have higher energy than those generated in single-mode fibers as well.

4. Conclusions

In conclusion, we numerically provided a first look at the spatiotemporal similariton pulses’ evolution in passive MM-Fibers with Raman amplification. We presented these issues in a GRIN-F and STEP-F using the same configuration. Under the condition of fundamental mode excitation with the most initial energy, the similariton pulses have a temporal and spectral parabolic shape with a linear chirp and high energy in both MM-Fibers, although the mechanisms of the propagations between them are different. Compressions of the output amplified pulses lead to the generation of 255 and 340 fs pulses in the case of the GRIN-F and the STEP-F, respectively. This approach has the potential in a generation of ultra-short pulses with ~100 kW of peak power corresponding to an amplification factor of ~500. The transverse distribution intensity of the beams retains a Gaussian-like profile along both the MM-Fibers. However, the spatiotemporal evolutions, as well as the spatial beam profiles, are very different when the initial pulse energy is equally distributed among all the modes. We have found that in both MM-Fibers, similariton-like solutions exist, but they differ in their nature. In the case of the GRIN-F, the propagation is essentially single-mode since the amplification of the fundamental mode is much higher than the amplification of higher-order modes. The initial spatial beam profile is progressively cleaned into a bell-shaped beam, resembling that of the fundamental mode. These features can be useful for the new beam self-cleaning process in the GRIN-F using a spatiotemporal similariton evolution. In the case of the STEP-F, all the modes considered in the simulations have nearly similar amplification coefficients and the interplay between them along the propagation distance determines the spatial and temporal structure of the generated pulses. Moreover, we can also use this platform for the similariton generation for all the modes. From these results, we expect that similariton pulses generated in MM-Fibers will open new directions in studies of nonlinear wave propagation and can offer a new route to mode-area scaling for different applications with controllable spatiotemporal properties.