Phase-Shifting Projected Fringe Profilometry Using Binary-Encoded Patterns
Abstract
:1. Introduction
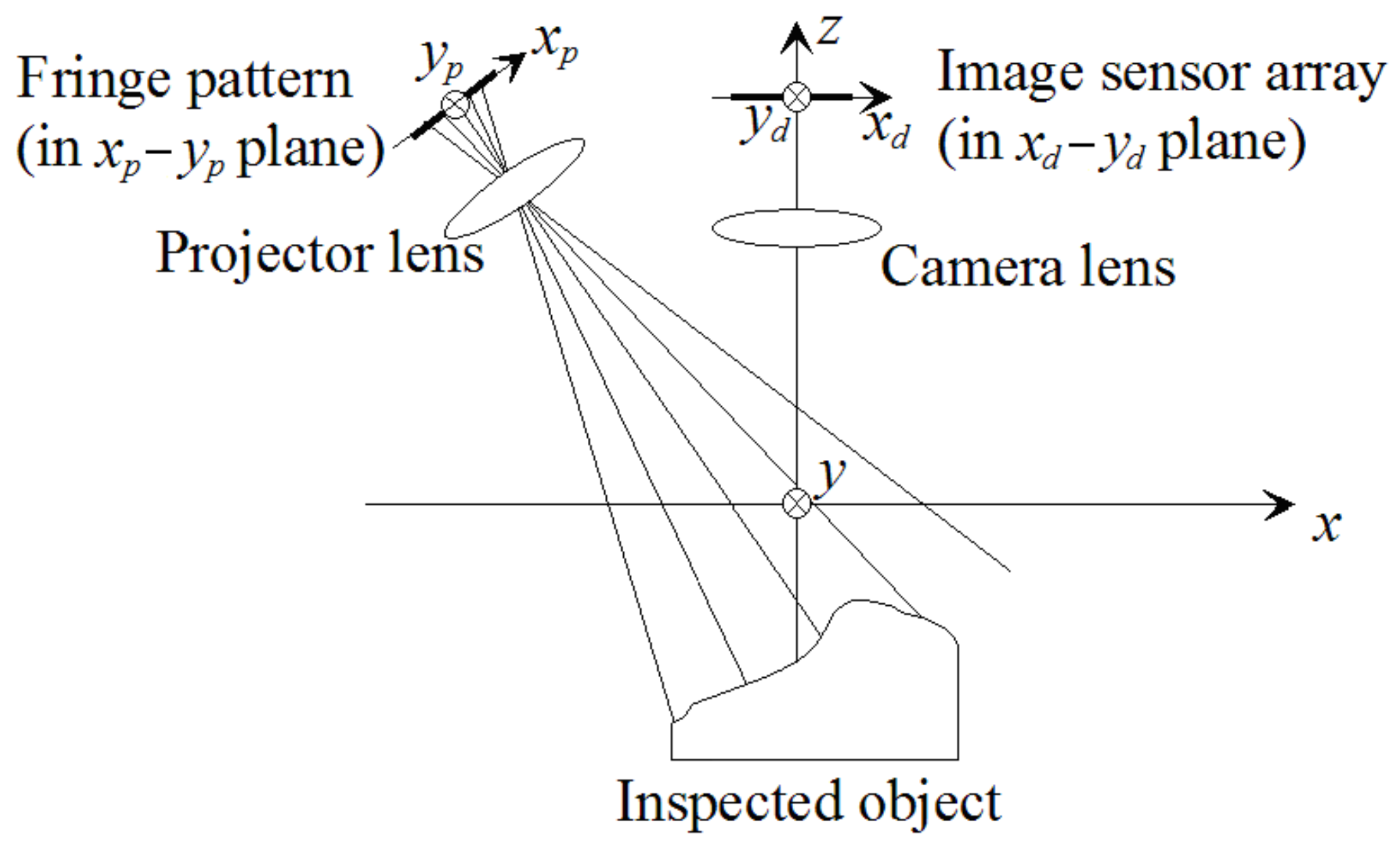
2. Materials and Methods
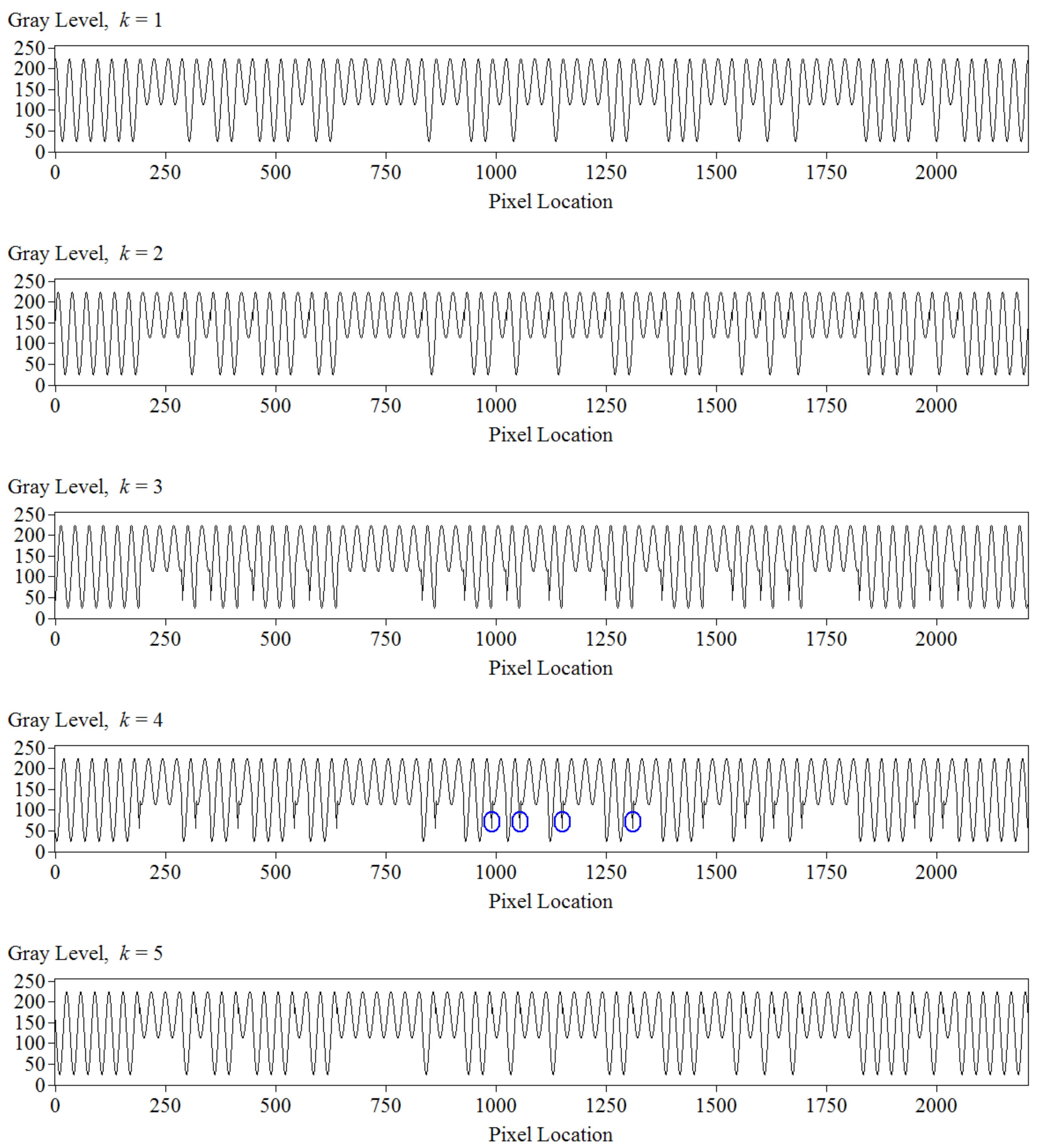
2.1. Fringe Encodingfor Phase-Shifting Projected Fringe Profilometry
2.2. Relationships between the Input and Observed Gray Levels
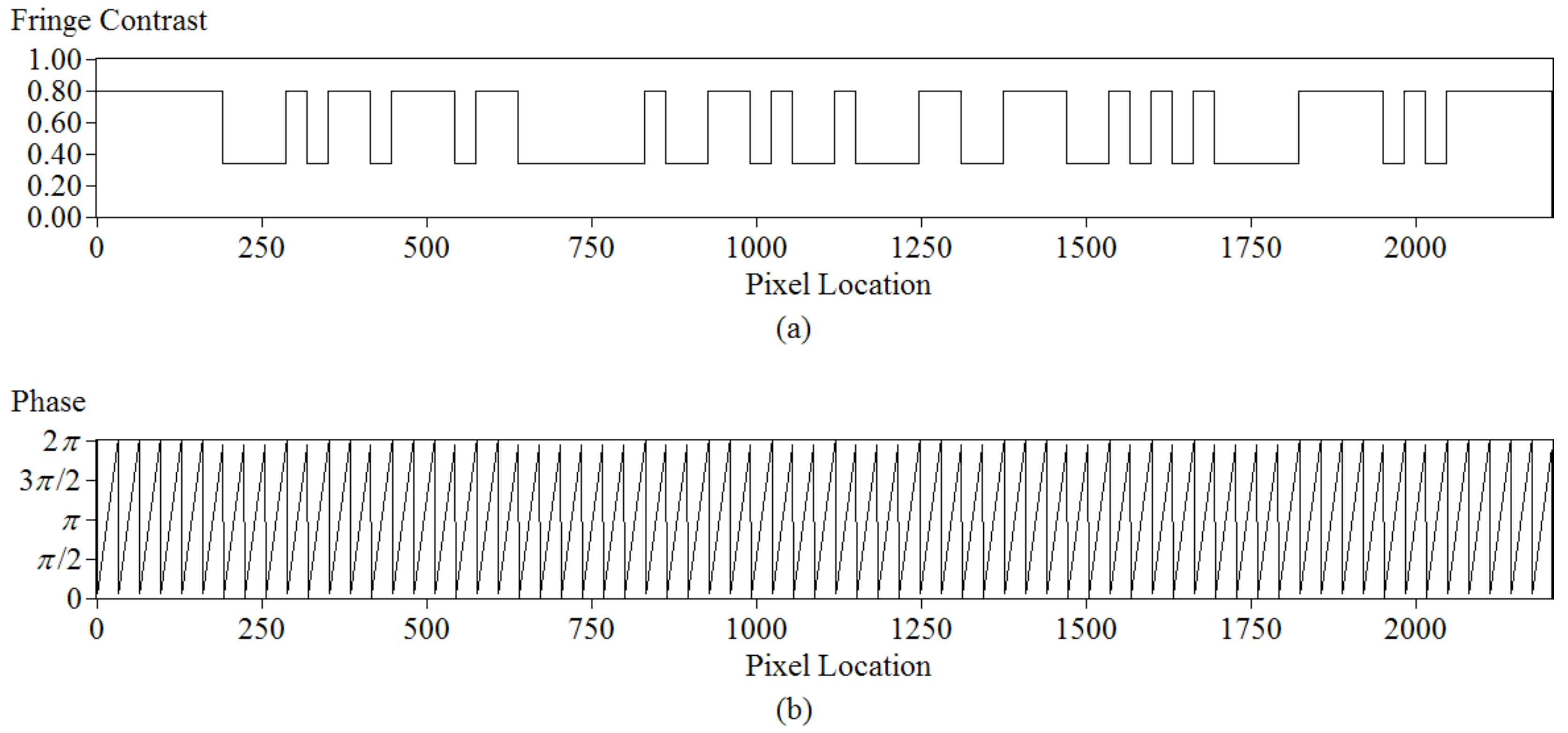
2.3. The Method Used forFringe Decodingand Unwrapping
2.4. Correspondences between the Absolute Phase Map and the Surface Profile
3. Results
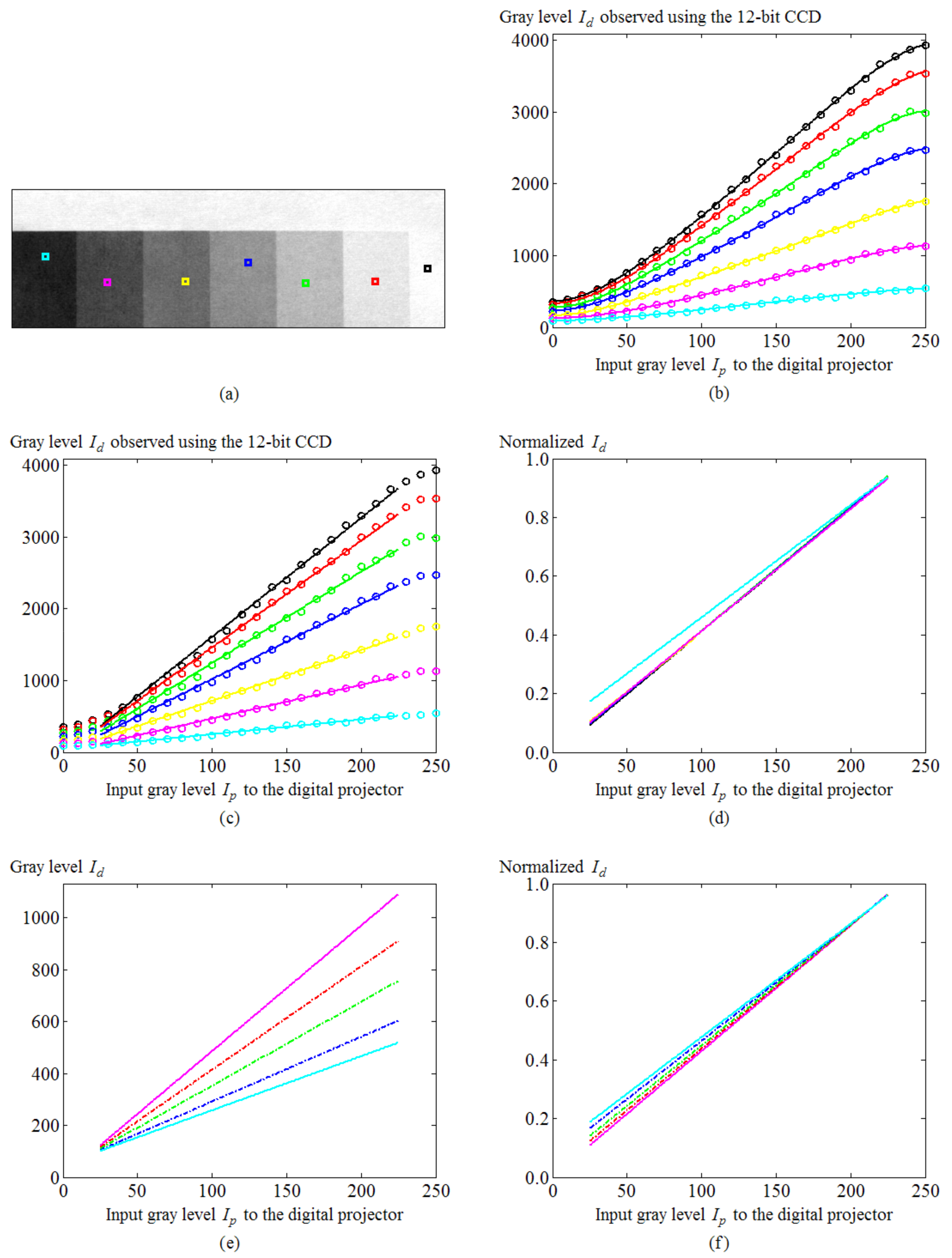
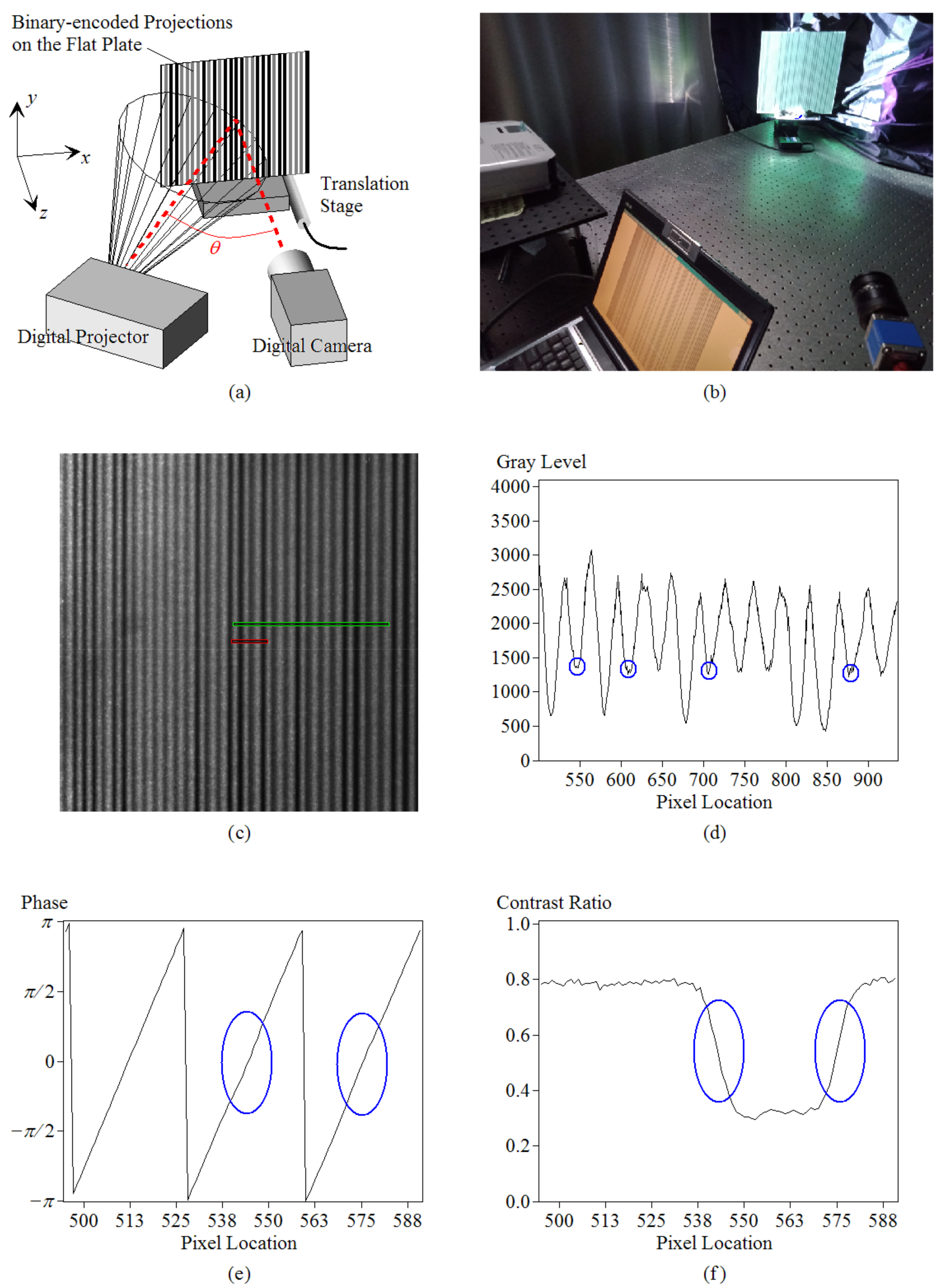
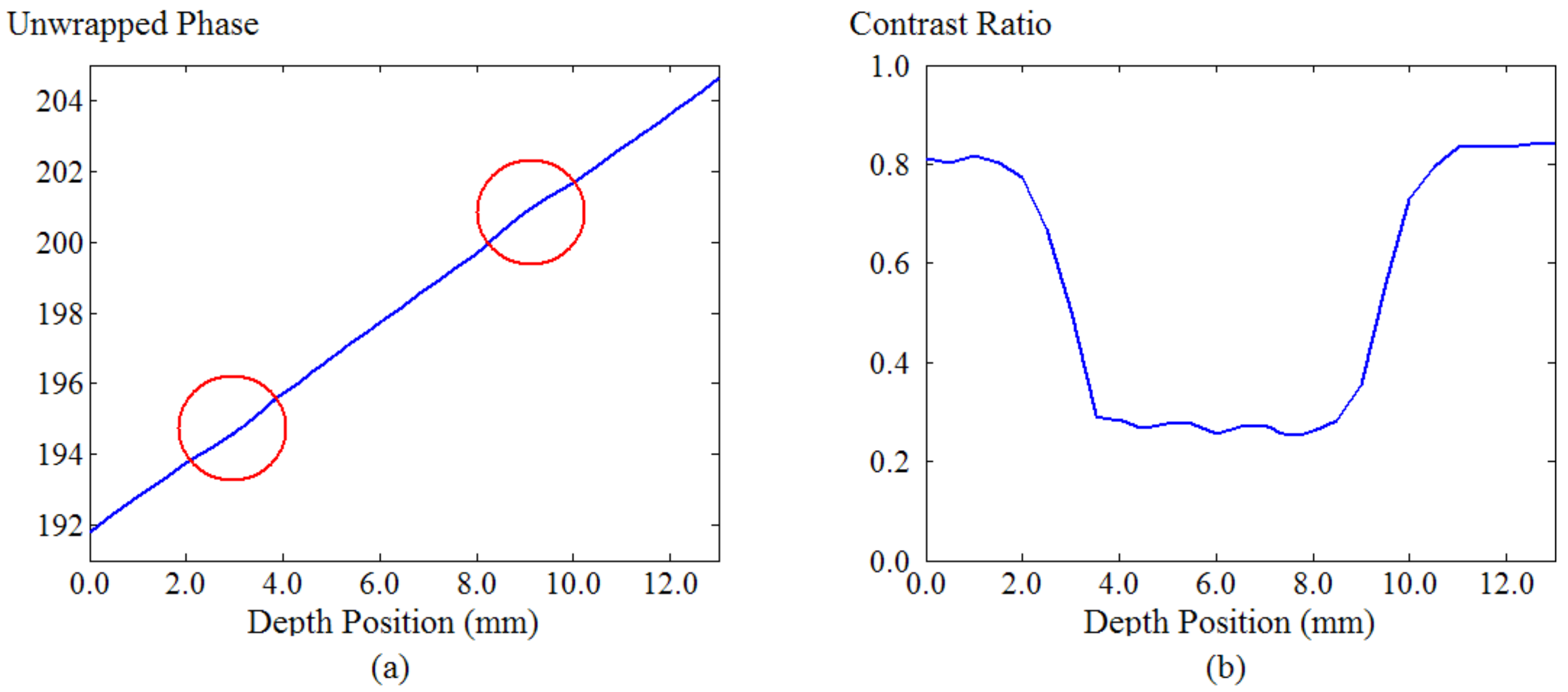
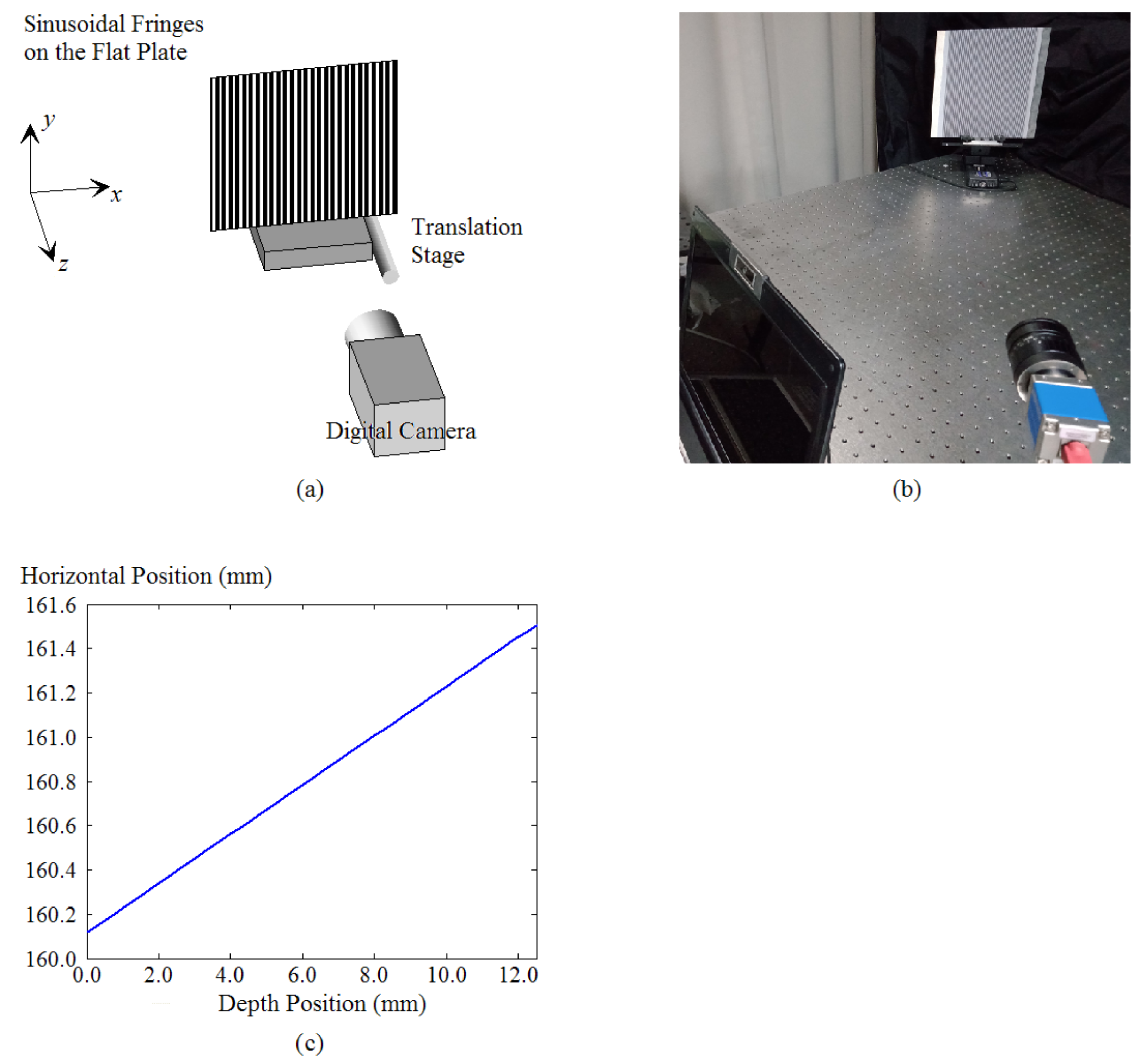
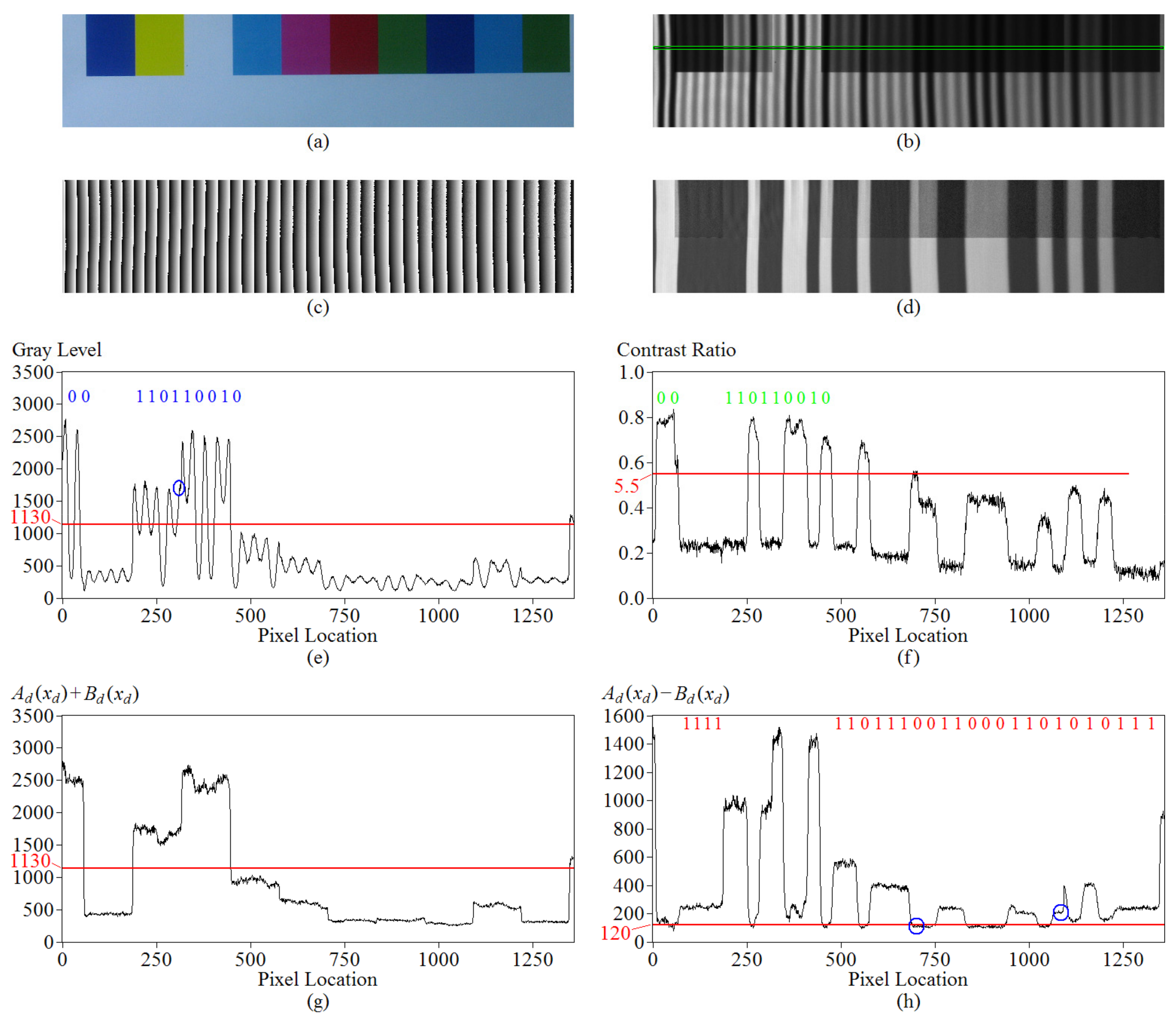
3.1. Calibrations
3.2. Systematic Accuracy
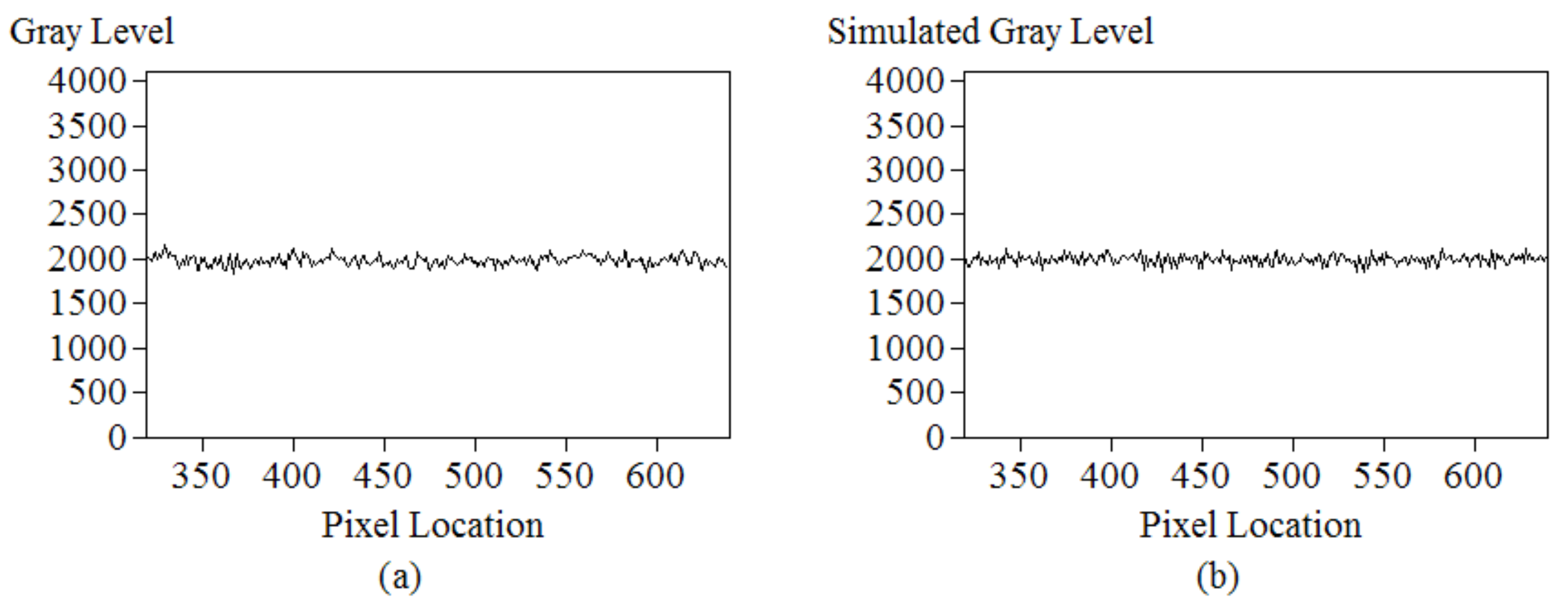
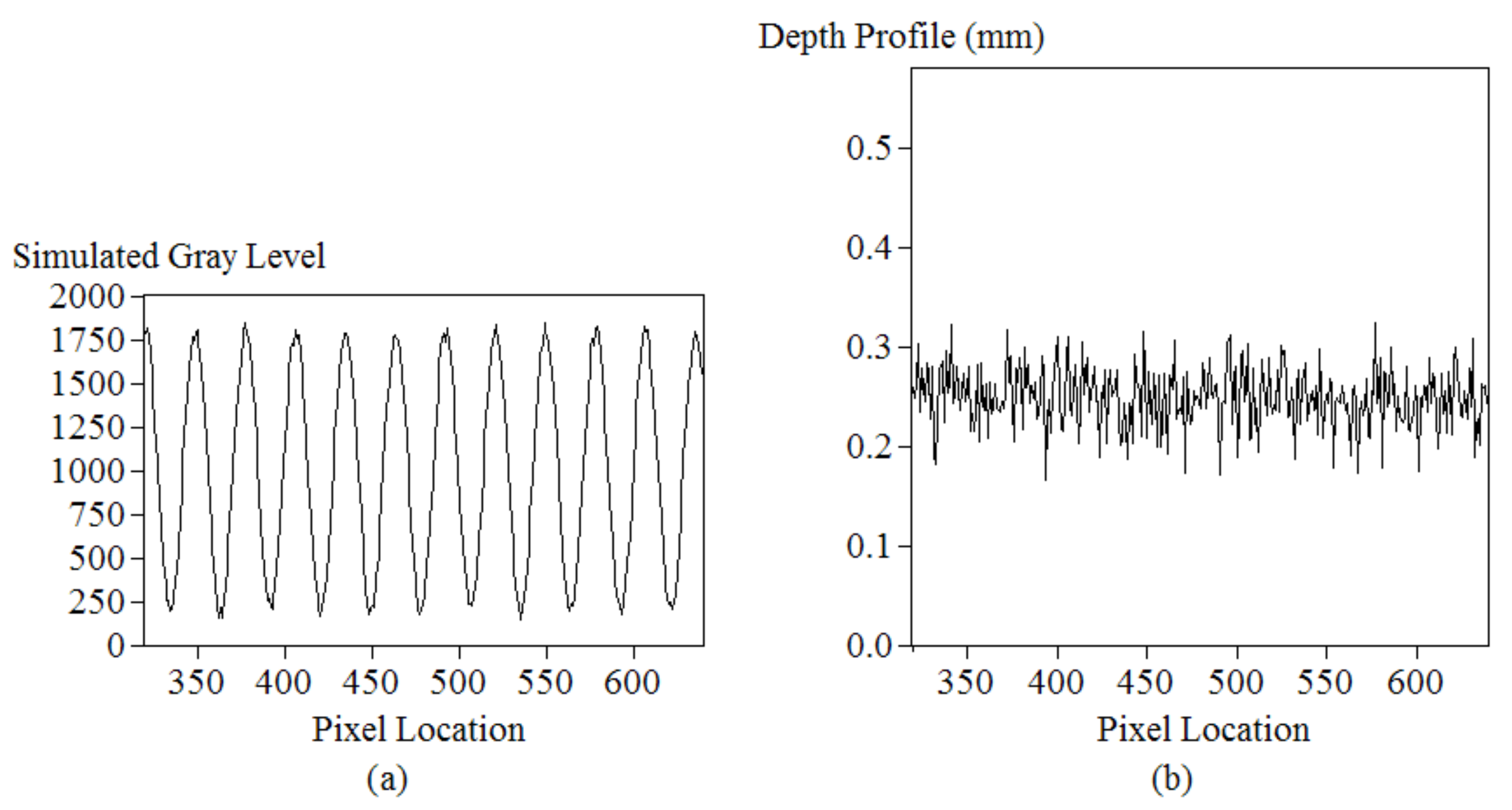
3.3. Simulations for Errors Caused by Reducing Fringe Contrasts
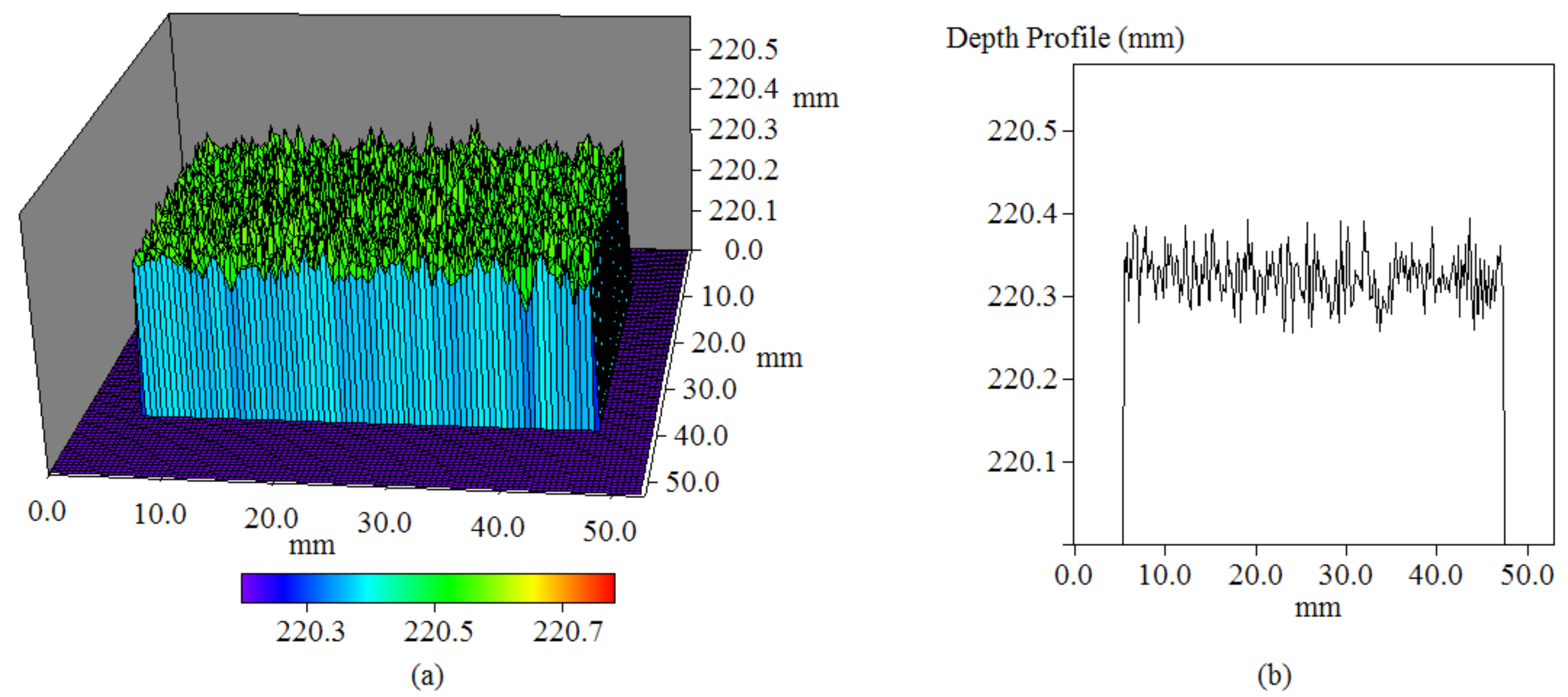
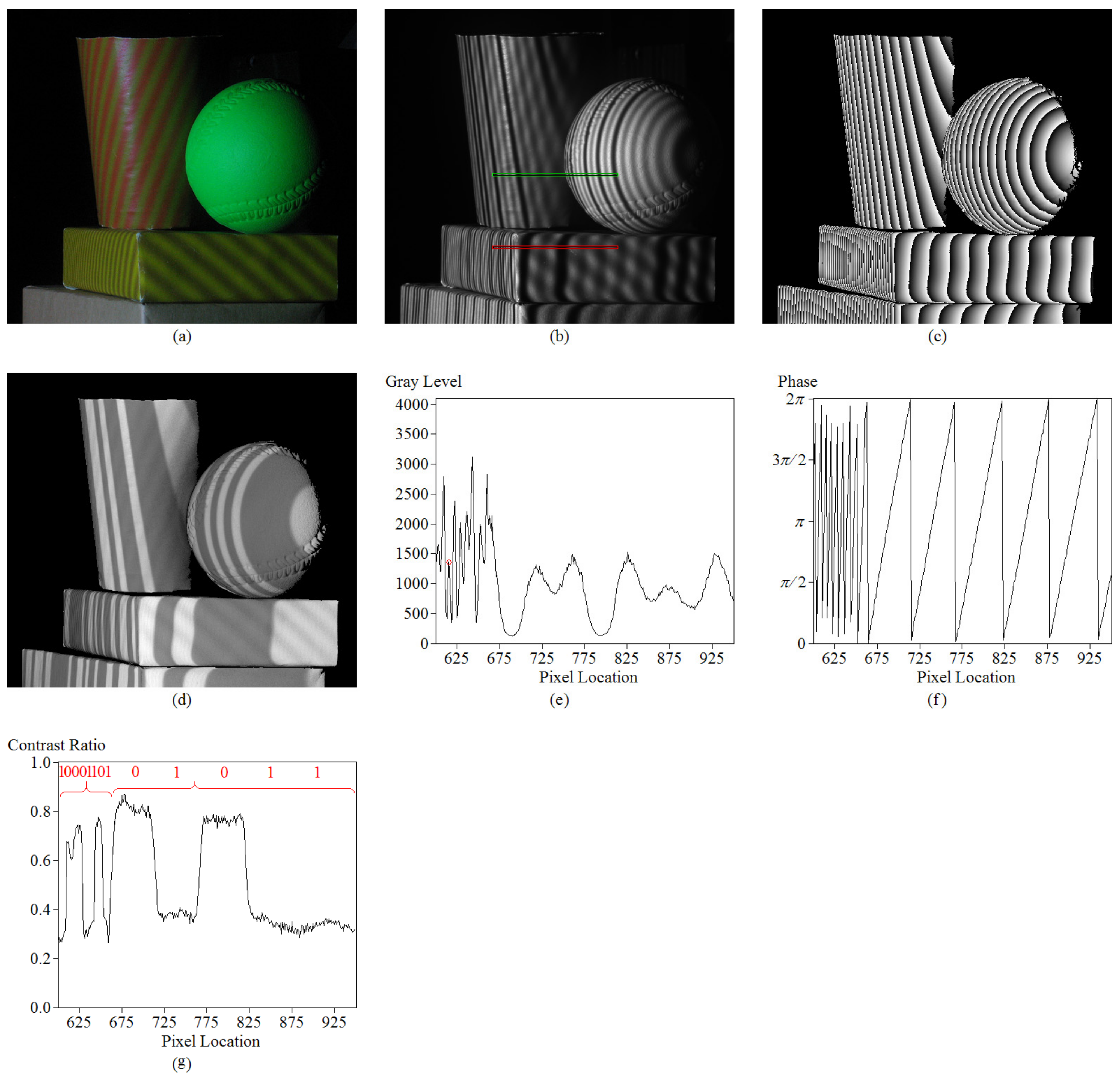
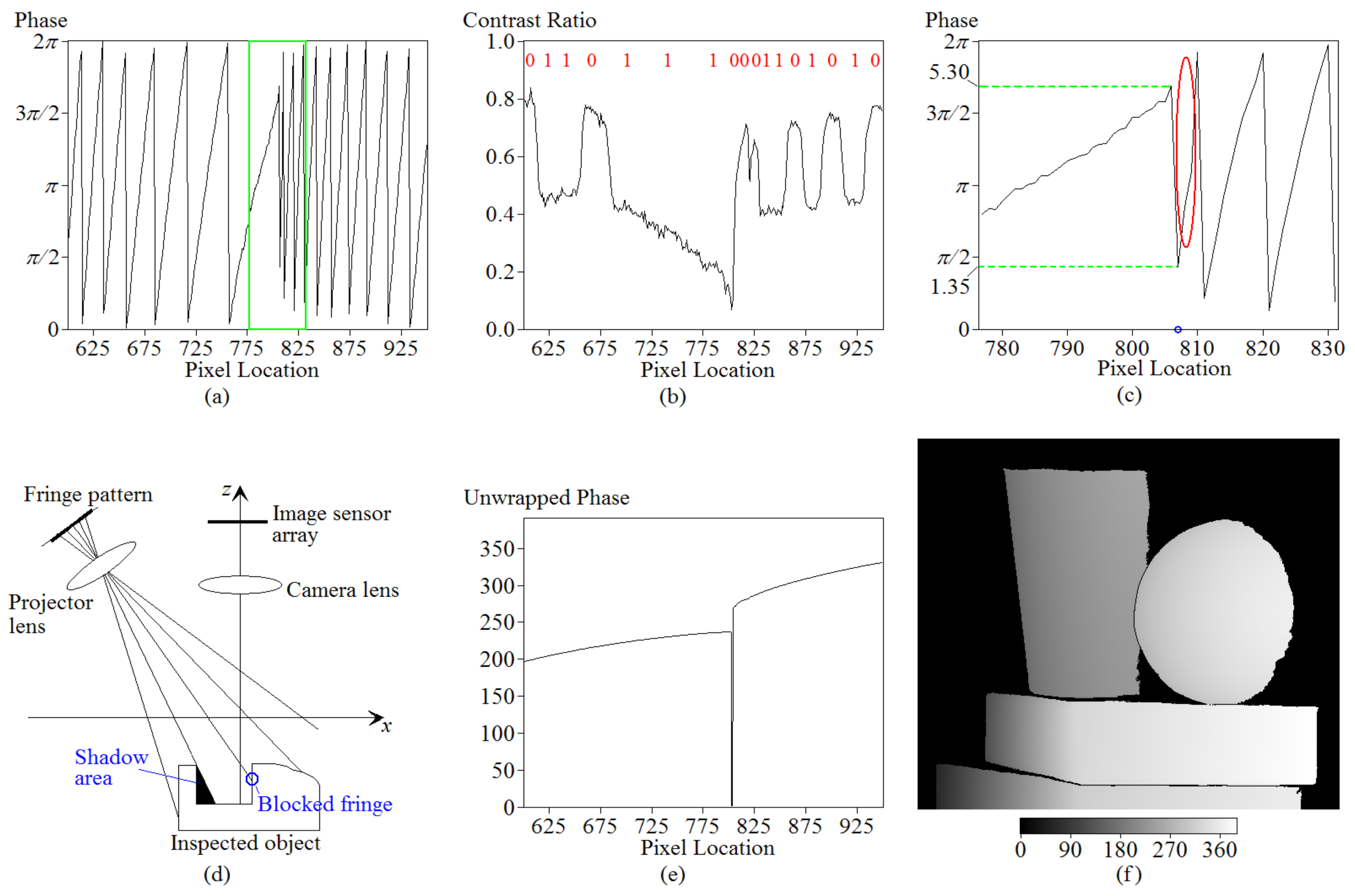
3.4. Profile Measurements for Surfaces with Depth Discontinuities and Periodic Textures
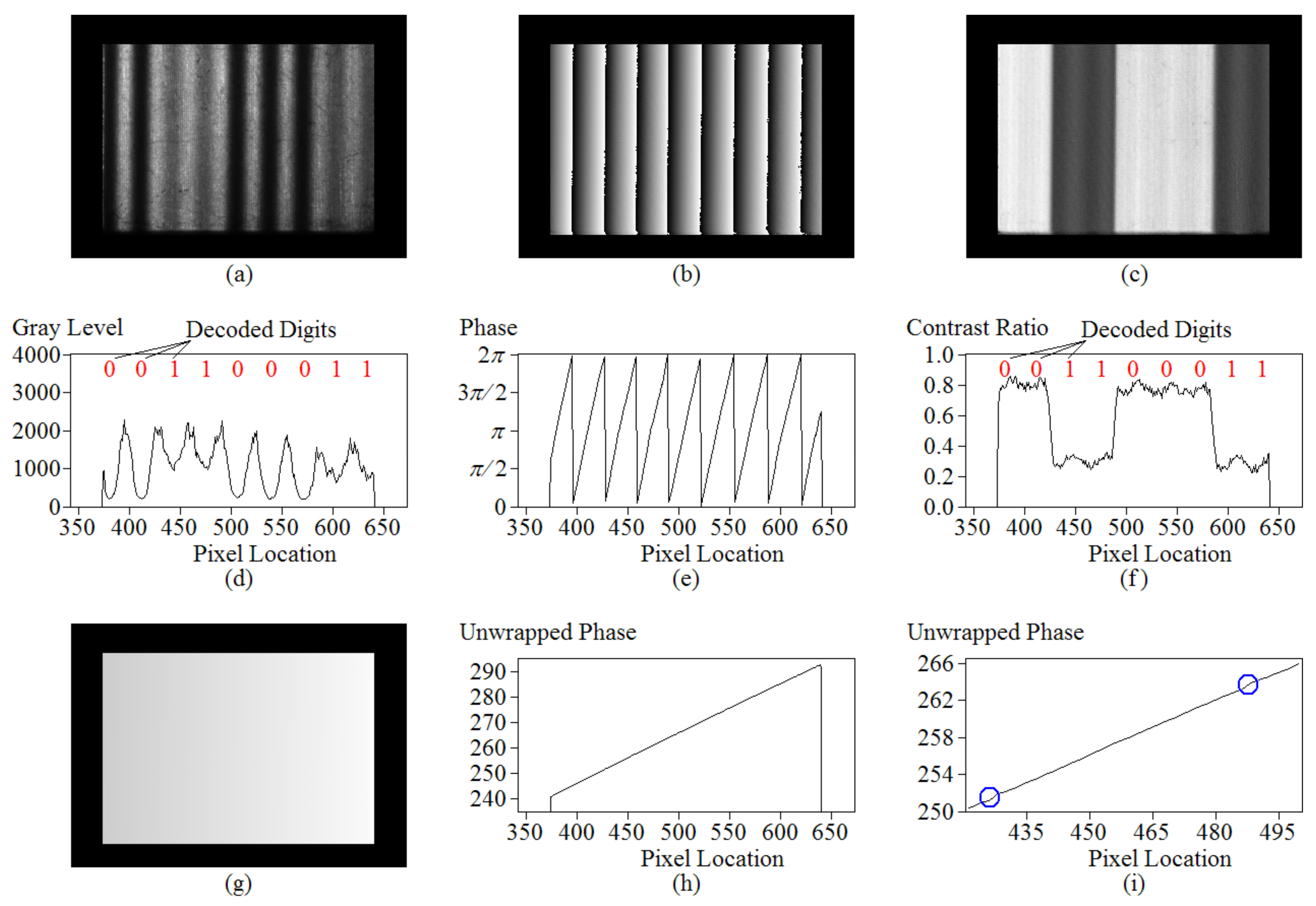
3.5. Fringe Decoding for Reflectance-Discontinuous Surfacesor Surfaces with Low Reflectance Coefficients
4. Discussion
- The reduced contrast produced more noise in the depth profile. A simulated relationship between the standard deviation of the depth profile and the contrast ratio of the input pattern is shown in Figure 15.
- Although the phase and contrast were extracted from the temporal projections, the fringe order was discerned based on spatial encoding schemes. Consequently, it suffered the same challenge as one-shot methods [23]: fringe orders cannot be known when the surface size is so small that the projected fringes cannot form a codeword.
- The measurement system was sensitive to light pollution. Before the profile measurement, calibrations for the relationship between the input gray level and the observed gray level were performed. Such calibrations included identifying the area of linearity illustrated in Figure 5c, defining the gray-level threshold to categorize the surfaces into two cases (i.e., the high reflectance and the low reflectance case), and finding the observed minimum gray level shown in Figure 5e. Then, the profile measurement was performed in the same circumstance, with the same exposure time of the CCD camera and the same size of the lens aperture. Consequently, it was sensitive to light pollution. Unwanted light pollution increased the DC gray level and reduced the contrast ratio. It caused the contrast threshold of 5.5 and the gray-level threshold of 1130 to no longer be available.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl. Opt. 1984, 23, 3105–3108. [Google Scholar] [CrossRef] [PubMed]
- Larkin, K.G.; Oreb, B.F. Design and assessment of symmetrical phase-shifting algorithms. J. Opt. Soc. Am. A 1992, 9, 1740–1748. [Google Scholar] [CrossRef] [Green Version]
- Su, X.-Y.; Von Bally, G.; Vukicevic, D. Phase-stepping grating profilometry: Utilization of intensity modulation analysis in complex objects evaluation. Opt. Commun. 1993, 98, 141–150. [Google Scholar] [CrossRef]
- Liu, H.; Su, W.-H.; Reichard, K.; Yin, S. Calibration-based phase-shifting projected fringe profilometry for accurate absolute 3D surface profile measurement. Opt. Commun. 2003, 216, 65–80. [Google Scholar] [CrossRef]
- Su, W.H.; Liu, H.; Reichard, K.; Yin, S.; Yu, F.T.S. Fabrication of digital sinusoidal gratings and precisely conytolled diffusive flats and their application to highly accurate projected fringe profilometry. Opt. Eng. 2003, 42, 1730–1740. [Google Scholar] [CrossRef]
- Creath, K. Step height measurement using two-wavelength phase-shifting interferometry. Appl. Opt. 1987, 26, 2810–2816. [Google Scholar] [CrossRef]
- Huntley, J.M.; Saldner, H.O. Temporal phase-unwrapping algorithm for automated inteferogram analysis. Appl. Opt. 1993, 32, 3047–3052. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, W.; Tan, Y. Phase-unwrapping algorithm for the measurement of three-dimensional object shapes. Appl. Opt. 1994, 33, 4497–4500. [Google Scholar] [CrossRef]
- Saldner, H.O.; Huntley, J.M. Temporal phase unwrapping: Application to surface profiling of discontinuous objects. Appl. Opt. 1997, 36, 2770–2775. [Google Scholar] [CrossRef]
- Hao, Y.; Zhao, Y.; Li, D. Multifrequency grating projection profilometry based on the nonlinear excess fraction method. Appl. Opt. 1999, 38, 4106–4110. [Google Scholar] [CrossRef]
- Li, E.B.; Peng, X.; Xi, J.; Chicharo, J.F.; Yao, J.Q.; Zhang, D.W. Multi-frequency and multiple phase-shift sinusoidal fringe projection for 3D profilometry. Opt. Express 2005, 13, 1561–1569. [Google Scholar] [CrossRef]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photon. 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Minou, M.; Kanade, T.; Sakai, T. A method of time-coded parallel planes of light for depth measurement. Trans. IECE Jpn. 1981, 64, 521–528. [Google Scholar]
- Sansoni, G.; Corini, S.; Lazzari, S.; Rodella, R.; Docchio, F. Three-dimensional imaging based on Gray-code light projection: Characterization of the measuring algorithm and development of a measuring system for industrial applications. Appl. Opt. 1997, 36, 4463–4472. [Google Scholar] [CrossRef] [Green Version]
- Brenner, C.; Boehm, J.; Guehring, J. Photogrammetric calibration and accuracy evaluation of a cross-pattern stripe projector. Proc. SPIE 1998, 3641, 164–172. [Google Scholar] [CrossRef]
- Sansoni, G.; Carocci, M.; Rodella, R. Three-dimensional vision based on a combination of gray-code and phase-shift light pro-jection: Analysis and compensation of the systematic errors. Appl. Opt. 1999, 38, 6565–6573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Zhang, S. Novel phase-coding method for absolute phase retrieval. Opt. Lett. 2012, 37, 2067–2069. [Google Scholar] [CrossRef]
- Zheng, D.; Da, F. Phase coding method for absolute phase retrieval with a large number of codewords. Opt. Express 2012, 20, 24139–24150. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Wang, Y.; Wang, Y.; Ma, M.; Zeng, C. Quantized phase coding and connected region labeling for absolute phase retrieval. Opt. Express 2016, 24, 28613–28624. [Google Scholar] [CrossRef]
- Boyer, K.L.; Kak, A.C. Color-Encoded Structured Light for Rapid Active Ranging. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 14–28. [Google Scholar] [CrossRef]
- Su, W.-H. Color-encoded fringe projection for 3D shape measurements. Opt. Express 2007, 15, 13167–13181. [Google Scholar] [CrossRef]
- Su, W.-H. Projected fringe profilometry using the area-encoded algorithm for spatially isolated and dynamic objects. Opt. Express 2008, 16, 2590–2596. [Google Scholar] [CrossRef]
- Su, W.-H.; Chen, S.-Y. One-shot profile inspection for surfaces with depth, color and reflectivity discontinuities. Opt. Express 2017, 25, 9999. [Google Scholar] [CrossRef]
- Guo, H.; He, H.; Chen, M. Gamma correction for digital fringe projection profilometry. Appl. Opt. 2004, 43, 2906–2914. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y.; Lau, D.L.; Hao, Q.; Hassebrook, L.G. Gamma model and its analysis for phase measuring profilometry. J. Opt. Soc. Am. A 2010, 27, 553–562. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.F. Gamma-distorted fringe image modeling and accurate gamma correction for fast phase measuring profilometry. Opt. Lett. 2011, 36, 154–156. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts & Company: Englewood, CO, USA, 2005; pp. 138–140. [Google Scholar]
- Zappa, E.; Busca, G. Comparison of eight unwrapping algorithms applied to Fourier-transform profilometry. Opt. Lasers Eng. 2008, 46, 106–116. [Google Scholar] [CrossRef]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 1983, 22, 3977–3982. [Google Scholar] [CrossRef]
- Brophy, C.P. Effect of intensity error correlation on the computed phase of phase-shifting interferometry. J. Opt. Soc. Am. A 1990, 7, 537–541. [Google Scholar] [CrossRef]
- Fischer, M.; Petz, M.; Tutsch, R. Statistical characterization of evaluation strategies for fringe projection systems by means of a model-based noise prediction. J. Sens. Sens. Syst. 2017, 6, 145–153. [Google Scholar] [CrossRef] [Green Version]



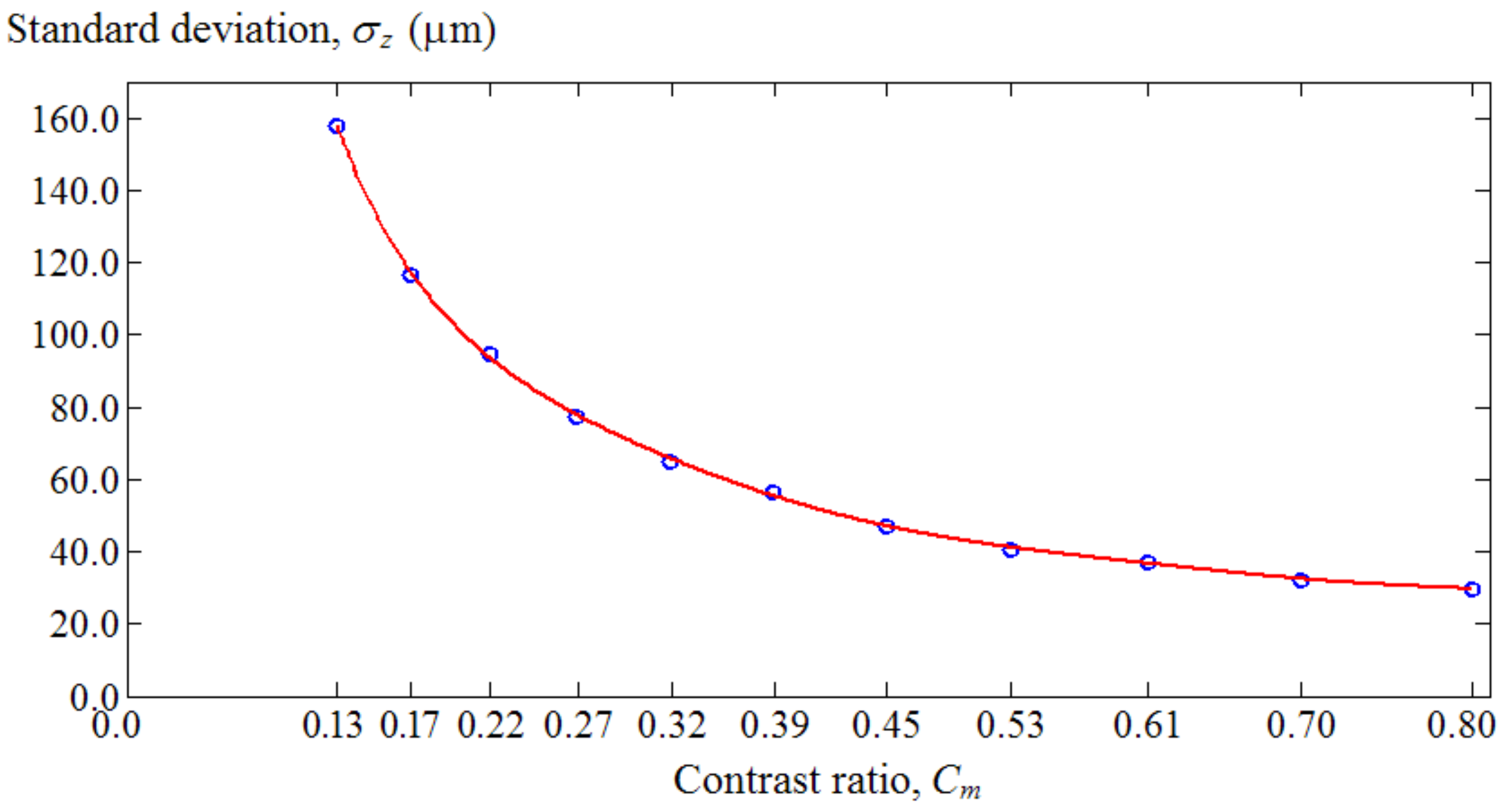

| Standard Deviation of the Depth Profile, σz (µm) | 158.0 | 116.4 | 94.9 | 77.3 | 64.7 | 56.4 | 47.0 | 40.6 | 37.0 | 32.3 | 29.6 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fringe amplitude in Ip(k), Bm | 25 | 32.5 | 40 | 47.5 | 55 | 62.5 | 70 | 77.5 | 85 | 92.5 | 100 |
| DC gray level in Ip(k), Am | 200 | 192.5 | 185 | 177.5 | 170 | 162.5 | 155 | 147.5 | 140 | 132.5 | 125 |
| Minimum gray level in Ip(k), Am − Bm | 175 | 160 | 145 | 130 | 115 | 100 | 85 | 70 | 55 | 40 | 25 |
| Contrast ratio, Cm = Bm/Am | 0.13 | 0.17 | 0.22 | 0.27 | 0.32 | 0.39 | 0.45 | 0.53 | 0.61 | 0.70 | 0.80 |
| Product of σz and Cm | 19.75 | 19.67 | 20.50 | 20.72 | 20.96 | 21.71 | 21.24 | 21.32 | 22.46 | 22.55 | 23.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, N.-J.; Su, W.-H. Phase-Shifting Projected Fringe Profilometry Using Binary-Encoded Patterns. Photonics 2021, 8, 362. https://doi.org/10.3390/photonics8090362
Cheng N-J, Su W-H. Phase-Shifting Projected Fringe Profilometry Using Binary-Encoded Patterns. Photonics. 2021; 8(9):362. https://doi.org/10.3390/photonics8090362
Chicago/Turabian StyleCheng, Nai-Jen, and Wei-Hung Su. 2021. "Phase-Shifting Projected Fringe Profilometry Using Binary-Encoded Patterns" Photonics 8, no. 9: 362. https://doi.org/10.3390/photonics8090362
APA StyleCheng, N.-J., & Su, W.-H. (2021). Phase-Shifting Projected Fringe Profilometry Using Binary-Encoded Patterns. Photonics, 8(9), 362. https://doi.org/10.3390/photonics8090362





