SP-ILC: Concurrent Single-Pixel Imaging, Object Location, and Classification by Deep Learning
Abstract
:1. Introduction
- SP-ILC is the first image recognition system (to the best of our knowledge) to accurately locate and classify individual or multiple different-sized objects in a scene, even when objects overlap, using a single-pixel camera. Current state-of-the-art single-pixel classification systems with deep learning are able to identify and classify only a single object in a scene;
- SP-ILC is an end-to-end system based on multitask learning that concurrently detects images, locates objects, and classifies objects in a single process. In contrast to techniques that detect images and identify objects in separate processes, SP-ILC has a compact structure, uses shared feature maps, and has increased generalizability;
- We have made the code and dataset associated with this study available to other researchers as open source [45].
2. Methods
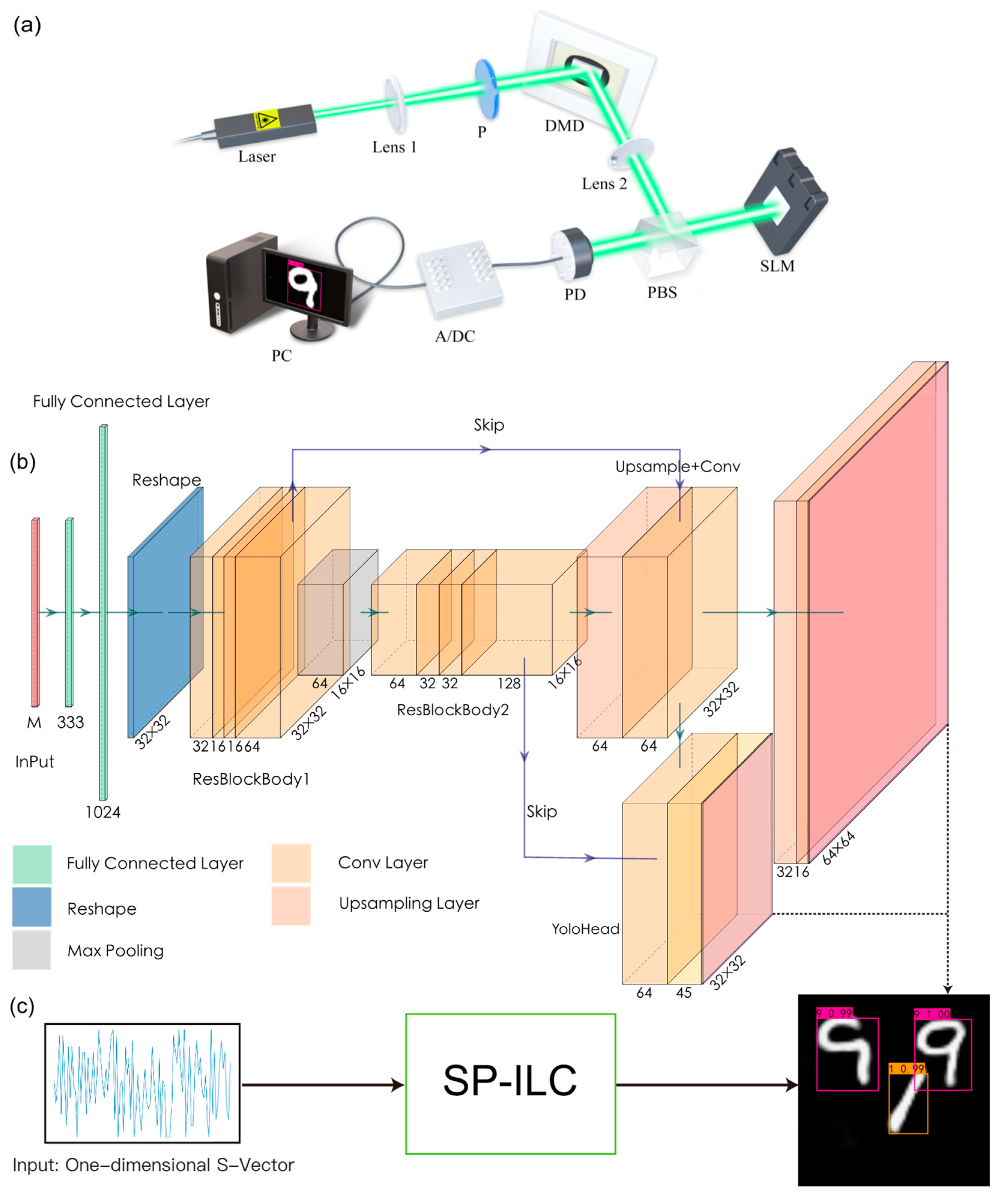
2.1. Experimental Setup and Structure of the Deep Neural Network
2.2. Loss Function
2.3. Dataset
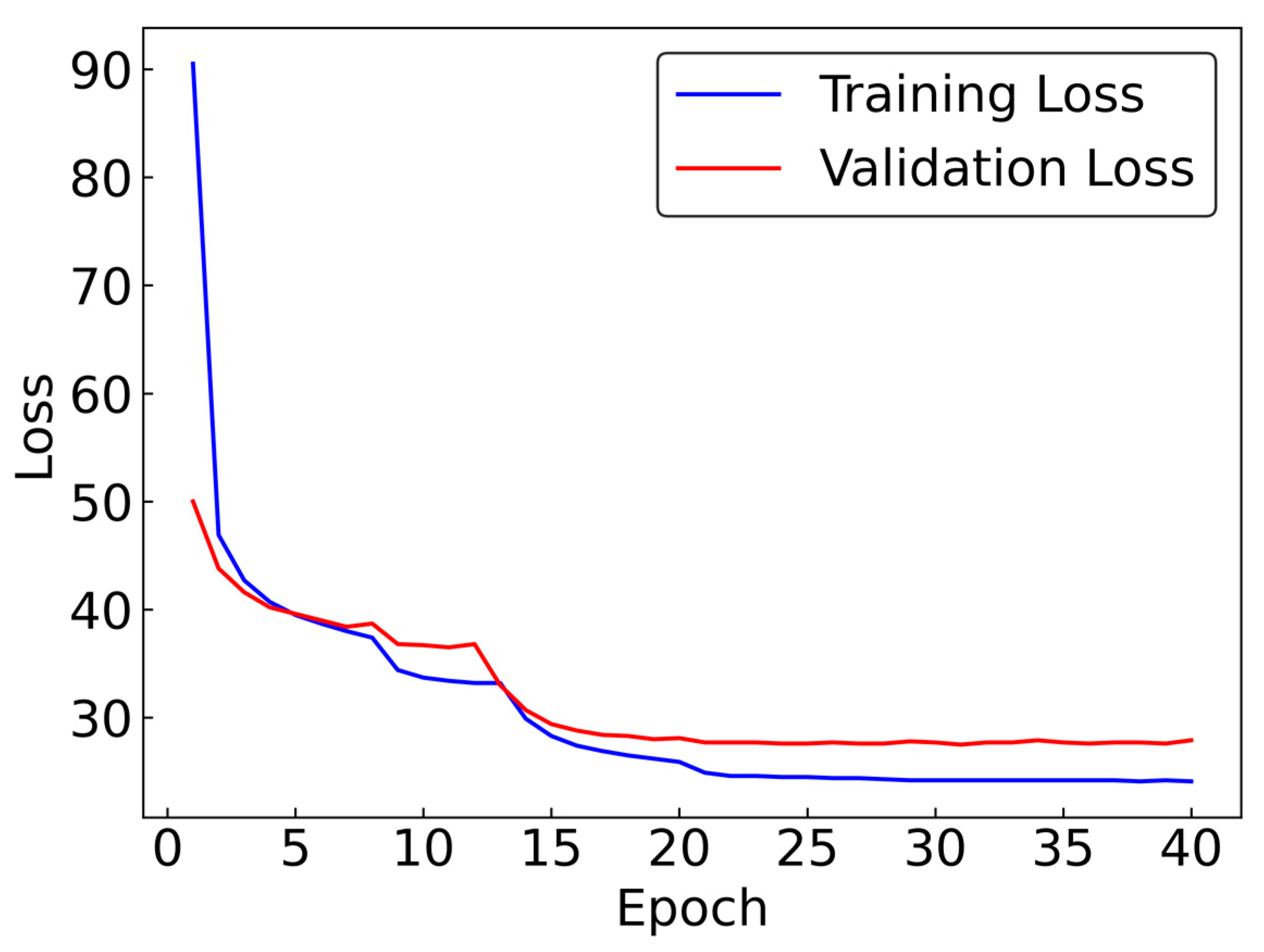
2.4. Training Parameters
2.5. Other Activities
3. Experimental Results and Analysis
3.1. Concurrent Imaging, Location, and Classification
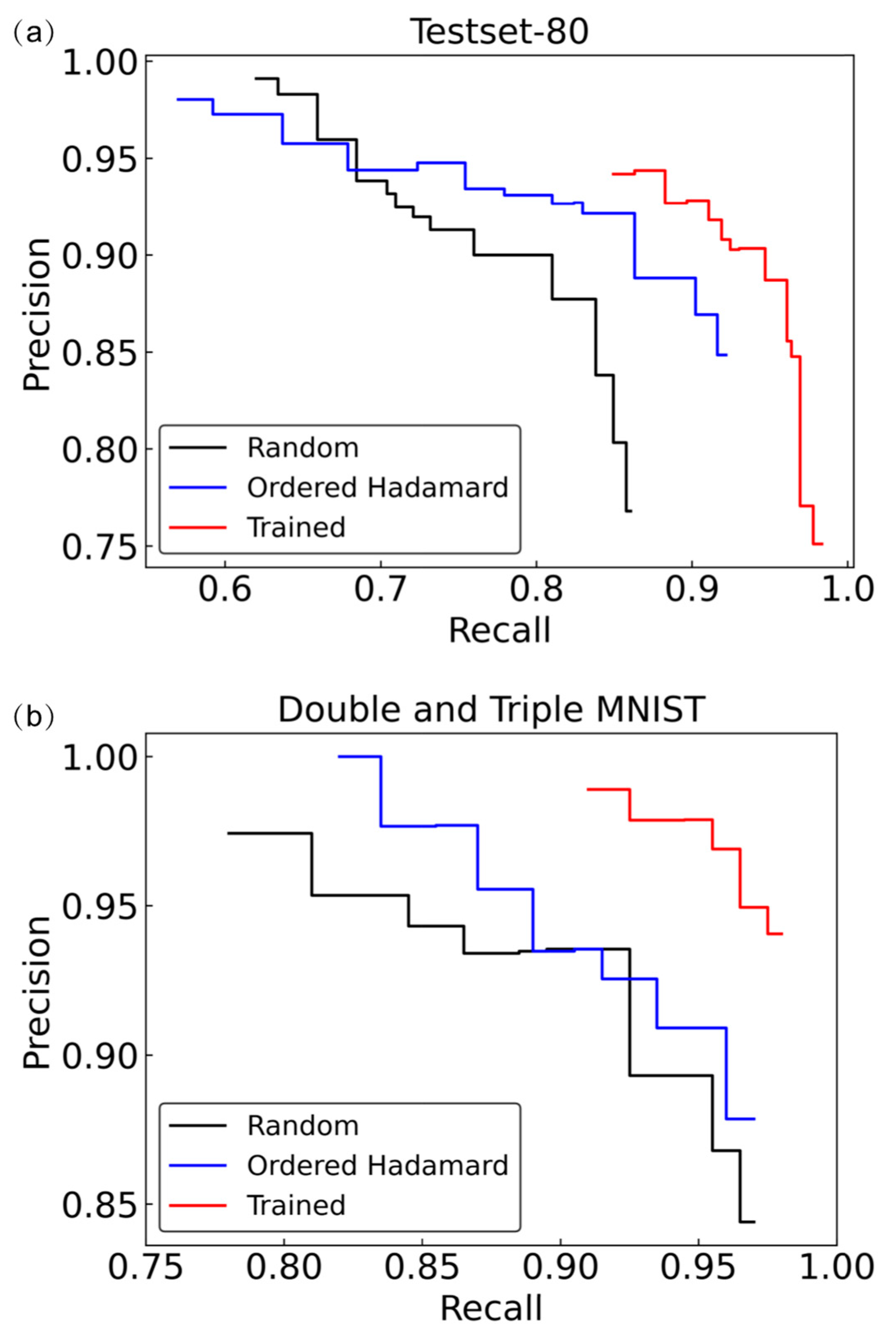
3.2. Precision–Recall Curve
3.3. Generalizaiton Ability
3.4. Optimal Patterns
3.5. Fashion MNIST
4. Discussions and Conclusions
4.1. Analysis of Imaging Ability
4.2. Analysis of Classification Ability
4.3. The Test Time for One Image
4.4. The End-to-End Multitask Learning System
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, M.J.; Zhang, J.M. Single-Pixel Imaging and Its Application in Three-Dimensional Reconstruction: A Brief Review. Sensors 2019, 19, 732. [Google Scholar] [CrossRef] [Green Version]
- Gibson, G.M.; Johnson, S.D.; Padgett, M. Single-pixel imaging 12 years on: A review. Opt. Express 2020, 28, 28190–28208. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Yiwen, E.; Williams, K.; Zhang, X.C.; Boyd, R. Spatial sampling of terahertz fields with sub-wavelength accuracy via probe beam encoding. Light Sci. Appl. 2019, 8, 55. [Google Scholar] [CrossRef] [Green Version]
- Radwell, N.; Mitchell, K.J.; Gibson, G.M.; Edgar, M.P.; Bowman, R.; Padgett, M.J. Single-pixel infrared and visible microscope. Optica 2014, 1, 285–289. [Google Scholar] [CrossRef]
- Zhang, A.X.; He, Y.H.; Wu, L.A.; Chen, L.M.; Wang, B.B. Tabletop X-ray ghost imaging with ultra-low radiation. Optica 2018, 5, 374–377. [Google Scholar] [CrossRef] [Green Version]
- Pittman, T.B.; Shih, Y.H.; Strekalov, D.V.; Sergienko, A.V. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429–R3432. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Katz, O.; Yaron, B.; Silberberg, Y. Compressive ghost imaging. Appl. Phys. Lett. 2009, 95, 131110. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Mathai, A.; Xu, X.; Wang, X. A Study into the Effects of Factors Influencing an Underwater, Single-Pixel Imaging System’s Performance. Photonics 2019, 6, 123. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.M.; Sun, M.J.; Chen, W.; Li, L.J. Illumination Calibration for Computational Ghost Imaging. Photonics 2021, 8, 59. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, W.X.; Liu, Y.P.; Ruan, D.; Li, J.L. Instant ghost imaging: Algorithm and on-chip Implementation. Opt. Express 2020, 28, 3607–3618. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Liu, J.; Zhang, W.X.; Ruan, D.; Li, J.L. Instant single-pixel imaging: On-chip real-time implementation based on the instant ghost imaging algorithm. OSA Contin. 2020, 3, 629–636. [Google Scholar] [CrossRef]
- Shang, R.; Hoffer-Hawlik, K.; Wang, F.; Situ, G.; Luke, G. Two-step training deep learning framework for computational imaging without physics priors. Opt. Express 2021, 29, 15239–15254. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.J.; Edgar, M.P.; Gibson, G.M.; Sun, B.; Radwell, N.; Lamb, R.; Padgett, M.J. Single-pixel three-dimensional imaging with time-based depth resolution. Nat. Commun. 2016, 7, 12010. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Bian, L.; Zhang, J. Depth acquisition in single-pixel imaging with multiplexed illumination. Opt. Express 2021, 29, 4866–4874. [Google Scholar] [CrossRef] [PubMed]
- Gong, W.; Zhao, C.; Yu, H.; Chen, M.; Xu, W.; Han, S. Three-dimensional ghost imaging lidar via sparsity constraint. Sci. Rep. 2016, 6, 26133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Chen, H.; Jiang, W.; Li, X.; Chen, X.; Meng, X.; Tian, P.; Sun, B. Optical encryption for visible light communication based on temporal ghost imaging with a micro-LED. Opt. Lasers Eng. 2020, 134, 106290. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Shrestha, A.; Mahmood, A. Review of Deep Learning Algorithms and Architectures. IEEE Access 2019, 7, 53040–53065. [Google Scholar] [CrossRef]
- Zoran, D.; Chrzanowski, M.; Huang, P.S.; Gowal, S.; Kohli, P. Towards Robust Image Classification Using Sequential Attention Models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9483–9492. [Google Scholar]
- Xiao, Y.; Tian, Z.; Yu, J.; Zhang, Y.; Liu, S.; Du, S.; Lan, X. A review of object detection based on deep learning. Multimed. Tools Appl. 2020, 79, 23729–23791. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Li, X.S.; Yue, T.Z.; Huang, X.P.; Yang, Z.; Xu, G. BAGS: An automatic homework grading system using the pictures taken by smart phones. arXiv 2019, arXiv:1906.03767. [Google Scholar]
- Xu, G.; Song, Z.G.; Sun, Z.; Ku, C.; Yang, Z.; Liu, C.C.; Wang, S.H.; Ma, J.P.; Xu, W. Camel: A weakly supervised learning framework for histopathology image segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019; pp. 10682–10691. [Google Scholar]
- Goda, K.; Jalali, B.; Lei, C.; Situ, G.; Westbrook, P. AI boosts photonics and vice versa. APL Photonics 2020, 5, 070401. [Google Scholar] [CrossRef]
- Bian, T.; Yi, Y.; Hu, J.; Zhang, Y.; Gao, L. A residual-based deep learning approach for ghost imaging. Sci. Rep. 2020, 10, 12149. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wang, R.; Zhao, G.; Xiao, H.; Zhang, X. Sub-nyquist computational ghost imaging with deep learning. Opt. Express 2020, 28, 3846–3853. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.; Chen, M.; Cheng, L.; Xiao, H.; Xu, L.; Wang, D.; Liang, J.; Xu, Y. Hybrid neural network-based adaptive computational ghost imaging. Opt. Lasers Eng. 2021, 140, 106529. [Google Scholar] [CrossRef]
- Wu, H.; Wang, R.; Zhao, G.; Xiao, H.; Liang, J.; Wang, D.; Tian, X.; Cheng, L.; Zhang, X. Deep-learning denoising computational ghost imaging. Opt. Lasers Eng. 2020, 134, 106183. [Google Scholar] [CrossRef]
- Latorre-Carmona, P.; Traver, V.J.; Sánchez, J.S.; Tajahuerce, E. Online reconstruction-free single-pixel image classification. Image Vis. Comput. 2019, 86, 28–37. [Google Scholar] [CrossRef]
- Ducros, N.; Mur, A.L.; Peyrin, F. A completion network for reconstruction from compressed acquisition. In Proceedings of the 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; pp. 619–623. [Google Scholar]
- Mur, A.; Leclerc, P.; Peyrin, F.; Ducros, N. Single-pixel image reconstruction from experimental data using neural networks. Opt. Express 2021, 29, 17097–17110. [Google Scholar] [CrossRef] [PubMed]
- Lyu, M.; Wang, W.; Wang, H.; Wang, H.; Li, G.; Chen, N.; Situ, G. Deep-learning-based ghost imaging. Sci. Rep. 2017, 7, 1–6. [Google Scholar] [CrossRef]
- Jiao, S. Fast object classification in single-pixel imaging. In Proceedings of the Sixth International Conference on Optical and Photonic Engineering (icOPEN), Shanghai, China, 8–11 May 2018; p. 108271O. [Google Scholar]
- Higham, C.F.; Murray-Smith, R.; Padgett, M.J.; Edgar, M.P. Deep learning for real-time single-pixel video. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, F.; Wang, H.; Wang, H.; Li, G.; Situ, G. Learning from simulation: An end-to-end deep-learning approach for computational ghost imaging. Opt. Express 2019, 27, 25560–25572. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Li, X.; Zheng, S.; Yao, M.; Zheng, G.; Zhong, J. Image-free classification of fast-moving objects using “learned” structured illumination and single-pixel detection. Opt. Express 2020, 28, 13269–13278. [Google Scholar] [CrossRef] [PubMed]
- Shimobaba, T.; Endo, Y.; Nishitsuji, T.; Takahashi, T.; Nagahama, Y.; Hasegawa, S.; Sano, M.; Hirayama, R.; Kakue, T.; Shiraki, A.; et al. Computational ghost imaging using deep learning. Opt. Commun. 2018, 413, 147–151. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Wang, G.; Dong, G.; Zhu, S.; Chen, H.; Zhang, A.; Xu, Z. Ghost imaging based on deep learning. Sci. Rep. 2018, 8, 6469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radwell, N.; Johnson, S.D.; Edgar, M.P.; Higham, C.F.; Murray-Smith, R.; Padgett, M.J. Deep learning optimized single-pixel lidar. Appl. Phys. Lett. 2019, 115, 231101. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- SP-ILC: Concurrent Single-Pixel Imaging, Object Location, and Classification by Deep Learning. Available online: https://github.com/Polarbeartnt/SP-ILC (accessed on 14 September 2021).
- Wang, L.; Zhao, S. Fast reconstructed and high-quality ghost imaging with fast Walsh–Hadamard transform. Photon. Res. 2016, 4, 240–244. [Google Scholar] [CrossRef]
- Iqbal, H. HarisIqbal88/PlotNeuralNet v1.0.0 (Version v1.0.0). Zenodo, 2018. [Google Scholar] [CrossRef]
- Le Cun, Y.; Cortes, C.; Burges, C.J.C. The MNIST Database of Handwritten Digits. 1998. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 15 October 2020).
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1–4. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Zhu, R.; Yu, H.; Tan, Z.; Lu, R.; Han, S.; Huang, Z.; Wang, J. Ghost imaging based on Y-net: A dynamic coding and decoding approach. Opt. Express 2020, 28, 17556–17569. [Google Scholar] [CrossRef]
- Buckland, M.; Gey, F. The relationship between recall and precision. J. Am. Soc. Inf. Sci. 1994, 45, 12–19. [Google Scholar] [CrossRef]
- Torgo, L.; Ribeiro, R. Precision and recall for regression. In Proceedings of the International Conference on Discovery Science, Porto, Portugal, 3–5 October 2009; pp. 332–346. [Google Scholar]
- Yu, W.K. Super sub-nyquist single-pixel imaging by means of cake-cutting hadamard basis sort. Sensors 2019, 19, 4122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Hoshi, I.; Shimobaba, T.; Kakue, T.; Ito, T. Single-pixel imaging using a recurrent neural network combined with convolutional layers. Opt. Express 2020, 28, 34069–34078. [Google Scholar] [CrossRef] [PubMed]
- Metz, C.E. Basic principles of ROC analysis. Semin. Nucl. Med. 1978, 8, 283–298. [Google Scholar] [CrossRef]
- Padilla, R.; Netto, S.L.; da Silva, E.A.B. A Survey on Performance Metrics for Object-Detection Algorithms. In Proceedings of the 2020 International Conference on Systems, Signals and Image Processing, Niteroi, Brazil, 1–3 July 2020; pp. 237–242. [Google Scholar]
- Caruana, R. Multitask learning. Mach. Learn 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 1440–1448. [Google Scholar]





| PSNR [dB] | SSIM | Precision | Recall | |
|---|---|---|---|---|
| Single object | 22.910 | 0.948 | 0.930 | 1.000 |
| Multiple objects | 16.487 | 0.820 | 0.808 | 0.799 |
| PSNR [dB] | SSIM | Precision | Recall | |
|---|---|---|---|---|
| Double MNIST | 20.798 | 0.915 | 0.925 | 0.950 |
| Triple MNIST | 19.443 | 0.876 | 0.943 | 0.867 |
| Pattern Name | Metrics of Image Quality | Single Object | Multiple Objects | Double MNIST | Triple MNIST |
|---|---|---|---|---|---|
| Random | PSNR [dB] | 24.815 | 17.320 | 20.798 | 19.443 |
| SSIM | 0.960 | 0.843 | 0.915 | 0.876 | |
| Ordered Hadamard | PSNR [dB] | 24.725 | 18.606 | 20.899 | 19.936 |
| SSIM | 0.968 | 0.901 | 0.936 | 0.920 | |
| Trained | PSNR [dB] | 29.247 | 22.145 | 25.158 | 22.908 |
| SSIM | 0.988 | 0.959 | 0.979 | 0.964 |
| Pattern Name | Single or Multiple Objects | PSNR [dB] | SSIM | Precision | Recall |
|---|---|---|---|---|---|
| Random | Single | 19.841 | 0.717 | 0.810 | 0.930 |
| Multiple | 19.927 | 0.805 | 0.791 | 0.812 | |
| Trained | Single | 20.793 | 0.755 | 0.847 | 0.930 |
| Multiple | 21.052 | 0.844 | 0.739 | 0.905 |
| Pattern Name | Metrics | CNN-Based | RNN-Based | SP-ILC |
|---|---|---|---|---|
| Random | PSNR [dB] | 9.283 | 15.274 | 19.841 |
| SSIM | 0.060 | 0.282 | 0.717 | |
| Trained | PSNR [dB] | 19.687 | 20.454 | 20.793 |
| SSIM | 0.490 | 0.498 | 0.755 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Bai, Y.-M.; Sun, L.-D.; Huang, K.-X.; Liu, J.; Ruan, D.; Li, J.-L. SP-ILC: Concurrent Single-Pixel Imaging, Object Location, and Classification by Deep Learning. Photonics 2021, 8, 400. https://doi.org/10.3390/photonics8090400
Yang Z, Bai Y-M, Sun L-D, Huang K-X, Liu J, Ruan D, Li J-L. SP-ILC: Concurrent Single-Pixel Imaging, Object Location, and Classification by Deep Learning. Photonics. 2021; 8(9):400. https://doi.org/10.3390/photonics8090400
Chicago/Turabian StyleYang, Zhe, Yu-Ming Bai, Li-Da Sun, Ke-Xin Huang, Jun Liu, Dong Ruan, and Jun-Lin Li. 2021. "SP-ILC: Concurrent Single-Pixel Imaging, Object Location, and Classification by Deep Learning" Photonics 8, no. 9: 400. https://doi.org/10.3390/photonics8090400
APA StyleYang, Z., Bai, Y.-M., Sun, L.-D., Huang, K.-X., Liu, J., Ruan, D., & Li, J.-L. (2021). SP-ILC: Concurrent Single-Pixel Imaging, Object Location, and Classification by Deep Learning. Photonics, 8(9), 400. https://doi.org/10.3390/photonics8090400





