A Method of Range Walk Error Correction in SiPM LiDAR with Photon Threshold Detection
Abstract
:1. Introduction
2. Theoretical Analysis
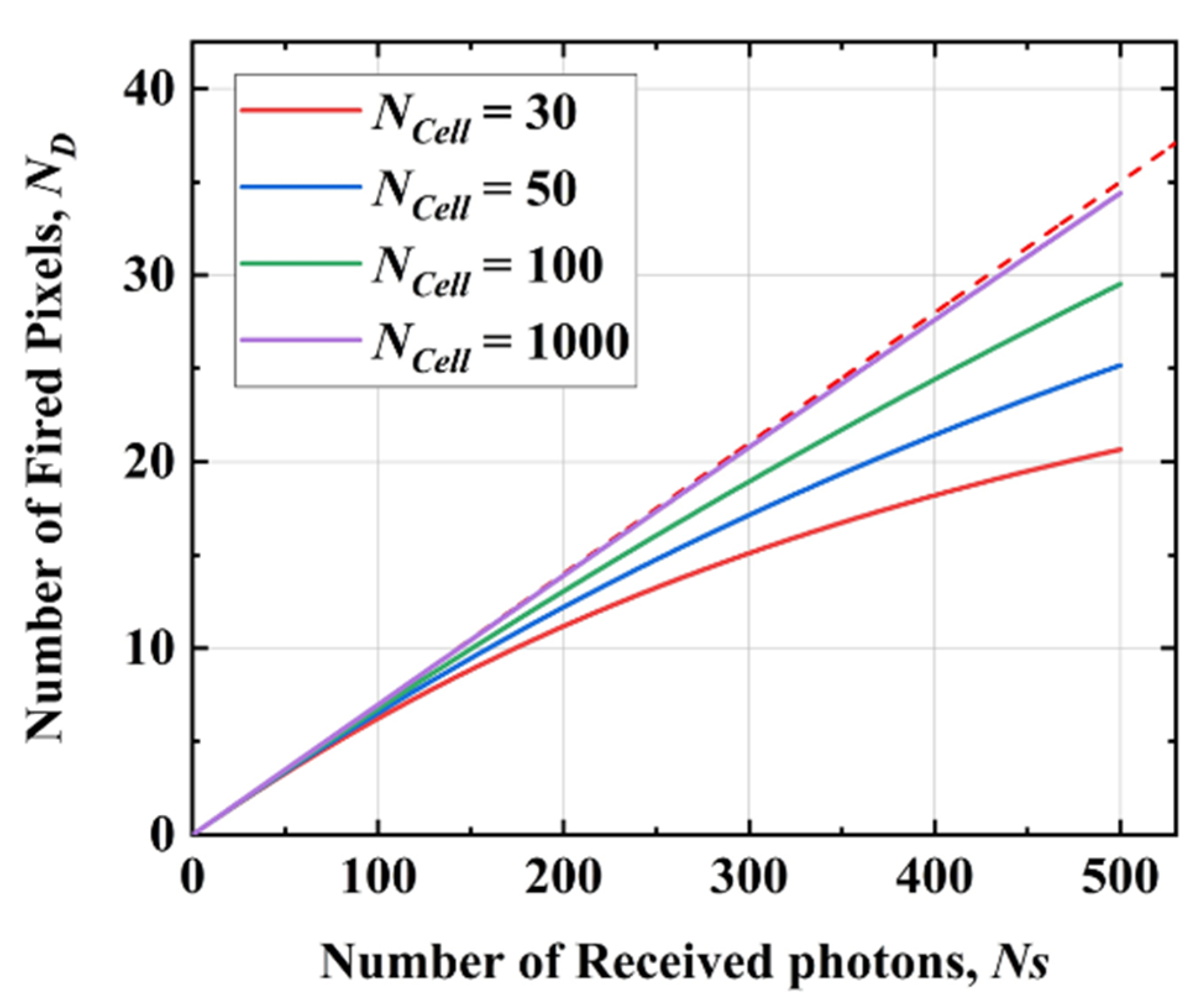
2.1. Laser Propagation Equation
2.2. SiPM Response Model
3. Experiments and Analysis
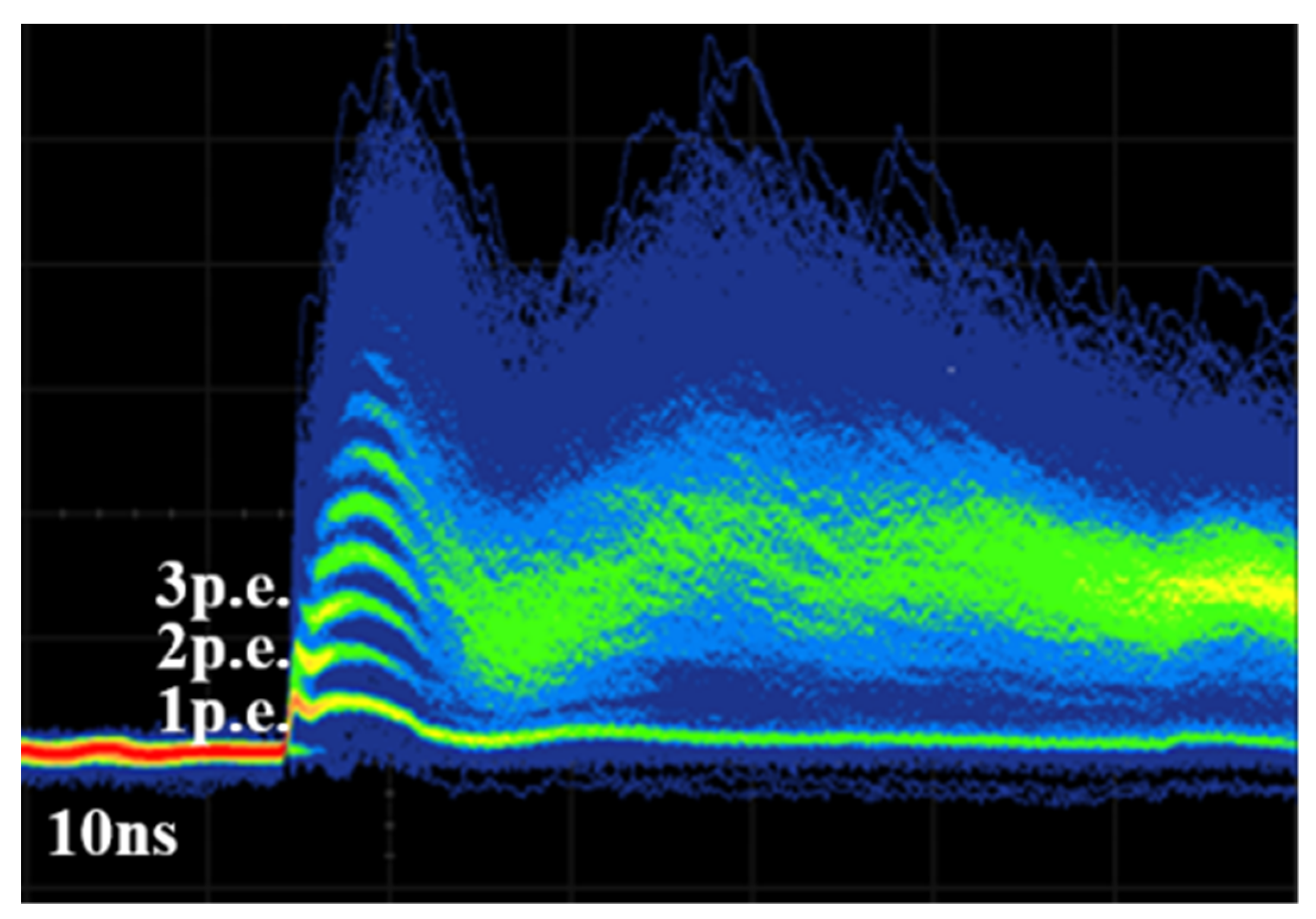
3.1. SiPM Response Measurement
3.2. Background Noise Measurement
3.3. TOF Measurement
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
TOF Measurement with 9% PDE (Photon Detection Efficiency) SiPM
| Parameter | S15639-1325PS | S13720-1325CS |
| PDE (905 nm) | 9% | 7% |
| Dark count rate | 0.7 MHz | 0.5 MHz |
| Crosstalk probability | 6% | 6% |
| Rise time | 500 ps | 500 ps |
| Gain | 1.7 × 106 | 1.1 × 106 |
| Number of microcells | 2120 | 2668 |

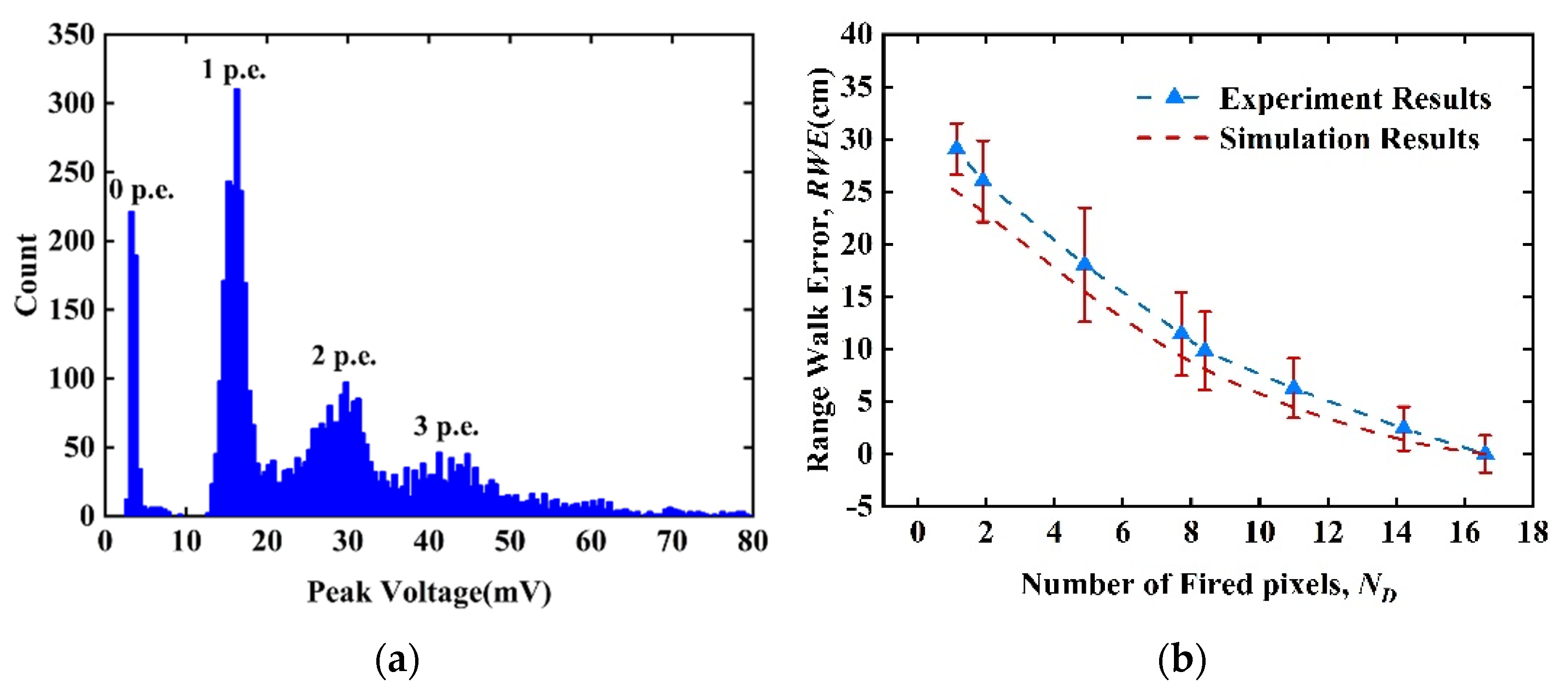
| ND | 1.13 | 1.91 | 4.88 | 7.72 | 8.40 | 11.00 | 14.22 |
| ETH (cm) | 29.07 | 26.00 | 18.03 | 11.43 | 9.81 | 6.26 | 2.42 |
| ETHC (cm) | 4.07 | 2.86 | 2.54 | 2.15 | 1.84 | 1.75 | 1.08 |
References
- Albota, M.A.; Heinrichs, R.M.; Kocher, D.G.; Fouche, D.G.; Player, B.E.; O’Brien, M.E.; Aull, B.F.; Zayhowski, J.J.; Mooney, J.; Willard, B.C.; et al. Three-dimensional imaging laser radar with a photon-counting avalanche photodiode array and microchip laser. Appl. Opt. 2002, 41, 7671–7678. [Google Scholar] [CrossRef] [Green Version]
- Tachella, J.; Altmann, Y.; Mellado, N.; McCarthy, A.; Tobin, R.; Buller, G.S.; Tourneret, J.-Y.; McLaughlin, S. Real-time 3D reconstruction from single-photon lidar data using plug-and-play point cloud denoisers. Nat. Commun. 2019, 10, 4984. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.P.; Ye, J.T.; Huang, X.; Jiang, P.Y.; Cao, Y.; Hong, Y.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.Z. Single-photon imaging over 200 km. Optica 2021, 8, 344. [Google Scholar] [CrossRef]
- Johnson, S.; Gatt, P.; Nichols, T. Analysis of Geiger-mode APD laser radars. In Proceedings of the Laser Radar Technology and Applications VIII, Orlando, FL, USA, 21 August 2003. [Google Scholar]
- Liang, Y.; Huang, J.; Ren, M.; Feng, B.; Chen, X.; Wu, E.; Wu, G.; Zeng, H. 1550-nm time-of-flight ranging system employing laser with multiple repetition rates for reducing the range ambiguity. Opt. Express 2014, 22, 4662–4670. [Google Scholar] [CrossRef] [Green Version]
- Massa, J.S.; Buller, G.S.; Walker, A.C.; Cova, S.; Umasuthan, M.; Wallace, A.M. Time-of-flight optical ranging system based on time-correlated single-photon counting. Appl. Opt. 1998, 37, 7298–7304. [Google Scholar] [CrossRef] [Green Version]
- Buller, G.; Wallace, A. Ranging and Three-Dimensional Imaging Using Time-Correlated Single-Photon Counting and Point-by-Point Acquisition. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 1006–1015. [Google Scholar] [CrossRef] [Green Version]
- Bao, Z.; Liang, Y.; Wang, Z.; Li, Z.; Wu, E.; Wu, G.; Zeng, H. Laser ranging at few-photon level by photon-number-resolving detection. Appl. Opt. 2014, 53, 3908–3912. [Google Scholar] [CrossRef]
- Buzhan, P.; Dolgoshein, B.; Filatov, L.; Ilyin, A.; Kantzerov, V.; Kaplin, V.; Karakash, A.; Kayumov, F.; Klemin, S.; Popova, E.; et al. Silicon photomultiplier and its possible applications. Nucl. Instrum. Methods Phys. Res. A 2003, 504, 48–52. [Google Scholar] [CrossRef]
- Collazuol, G.; Ambrosi, G.; Boscardin, M.; Corsi, F.; Betta, G.; Guerra, A.D.; Dinu, N.; Galimberti, M.; Giulietti, D.; Gizzi, L.A. Single photon timing resolution and detection efficiency of the IRST silicon photo-multipliers. Nucl. Instrum. Methods Phys. Res. A 2007, 581, 461–464. [Google Scholar] [CrossRef]
- Villa, F.; Severini, F.; Madonini, F.; Zappa, F. SPADs and SiPMs Arrays for Long-Range High-Speed Light Detection and Ranging (LiDAR). Sensors 2021, 21, 3839. [Google Scholar] [CrossRef]
- Haemisch, Y.; Frach, T.; Degenhardt, C.; Thon, A. Fully Digital Arrays of Silicon Photomultipliers (dSiPM)—A Scalable Alternative to Vacuum Photomultiplier Tubes (PMT). Phys. Procedia 2012, 37, 1546–1560. [Google Scholar] [CrossRef] [Green Version]
- Cohen, L.; Matekole, E.S.; Sher, Y.; Istrati, D.; Eisenberg, H.S.; Dowling, J.P. Thresholded quantum LIDAR: Exploiting photon-number-resolving detection. Phys. Rev. Lett. 2019, 123, 203601. [Google Scholar] [CrossRef] [Green Version]
- Yue, M.; Song, L.; Zhang, W.; Zhang, Z.; Liu, R.; Hua, W.X. Theoretical ranging performance model and range walk error correction for photon-counting lidars with multiple detectors. Opt. Express 2018, 26, 15924. [Google Scholar]
- Xu, L.; Zhang, Y.; Zhang, Y.; Yang, C.; Yang, X.; Zhao, Y. Restraint of range walk error in a Geiger-mode avalanche photodiode lidar to acquire high-precision depth and intensity information. Appl. Opt. 2016, 55, 1683–1687. [Google Scholar] [CrossRef]
- He, W.; Sima, B.; Chen, Y.; Dai, H.; Chen, Q.; Gu, G. A correction method for range walk error in photon counting 3D imaging LIDAR. Opt. Commun. 2013, 308, 211–217. [Google Scholar] [CrossRef]
- Min, S.O.; Hong, J.K.; Kim, T.H.; Hong, K.H.; Kim, B.W. Reduction of range walk error in direct detection laser radar using a Geiger mode avalanche photodiode. Opt. Commun. 2010, 283, 304–308. [Google Scholar]
- Chen, Z.; Li, X.; Li, X.; Ye, G.; Zhou, Z.; Lu, L.; Sun, T.; Fan, R.; Chen, D. A correction method for range walk error in time-correlated single-photon counting using photomultiplier tube. Opt. Commun. 2019, 434, 7–11. [Google Scholar] [CrossRef]
- Kilpel, A.; Ylitalo, J.; Mtt, K.; Kostamovaara, J. Timing discriminator for pulsed time-of-flight laser rangefinding measurements. Rev. Sci. Instrum. 1998, 69, 1978–1984. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Schmall, J.P.; Judenhofer, M.S.; Di, K.; Cherry, S.R. A Time-Walk Correction Method for PET Detectors Based on Leading Edge Discriminators. IEEE Trans. Radiat. Plasma Med. Sci. 2017, 1, 385. [Google Scholar] [CrossRef]
- Li, X.; Yang, B.; Xie, X.; Li, D.; Xu, L. Influence of waveform characteristics on LiDAR ranging accuracy and precision. Sensors 2018, 18, 1156. [Google Scholar] [CrossRef] [Green Version]
- Johnson, E.S. Effect of target surface orientation on the range precision of laser detection and ranging systems. J. Appl. Remote Sens. 2009, 3, 2527–2532. [Google Scholar] [CrossRef]
- Lim, H.C.; Zhang, Z.P.; Sung, K.P.; Park, J.U.; Choi, M. Modeling and Analysis of an Echo Laser Pulse Waveform for the Orientation Determination of Space Debris. Remote Sens. 2020, 12, 1659. [Google Scholar] [CrossRef]
- Kostamovaara, J.; Huikari, J.; Hallman, L.; Nissinen, I.; Nissinen, J.; Rapakko, H.; Avrutin, E.; Ryvkin, B. On Laser Ranging Based on High-Speed/Energy Laser Diode Pulses and Single-Photon Detection Techniques. IEEE Photonics J. 2015, 7, 1–15. [Google Scholar] [CrossRef]
- Daniel, G.F. Detection and false-alarm probabilities for laser radars that use Geiger-mode detectors. Appl. Opt. 2003, 42, 5388–5398. [Google Scholar]
- Renker, D.; Lorenz, E. Advances in solid state photon detectors. J. Instrum. 2009, 4, P04004. [Google Scholar] [CrossRef]
- Chen, L.H. On the convergence of Poisson binomial to Poisson distributions. Ann. Probab. 1974, 2, 178–180. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, R.; Qiu, J.; Liu, K. Wide dynamic laser ranging based on diode laser and photon-counting techniques. Appl. Opt. 2021, 60, 2716–2721. [Google Scholar] [CrossRef]
- Keysight Infiniium Oscilloscopes Programmer’s Guide. Available online: https://www.etesttool.com/downloads/pdf/Keysight/Keysight-DSAZ634A/Infiniium_prog_guide.pdf (accessed on 23 December 2021).

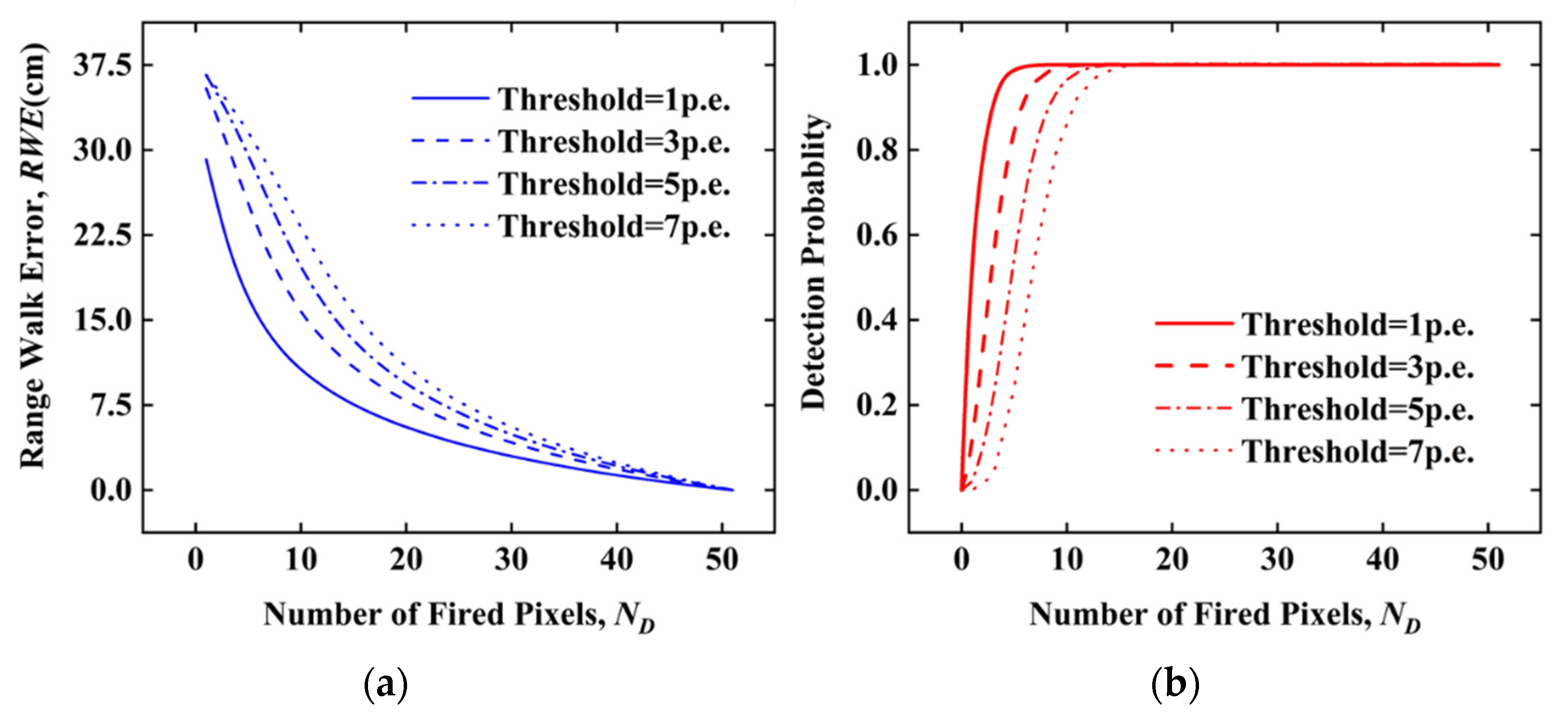


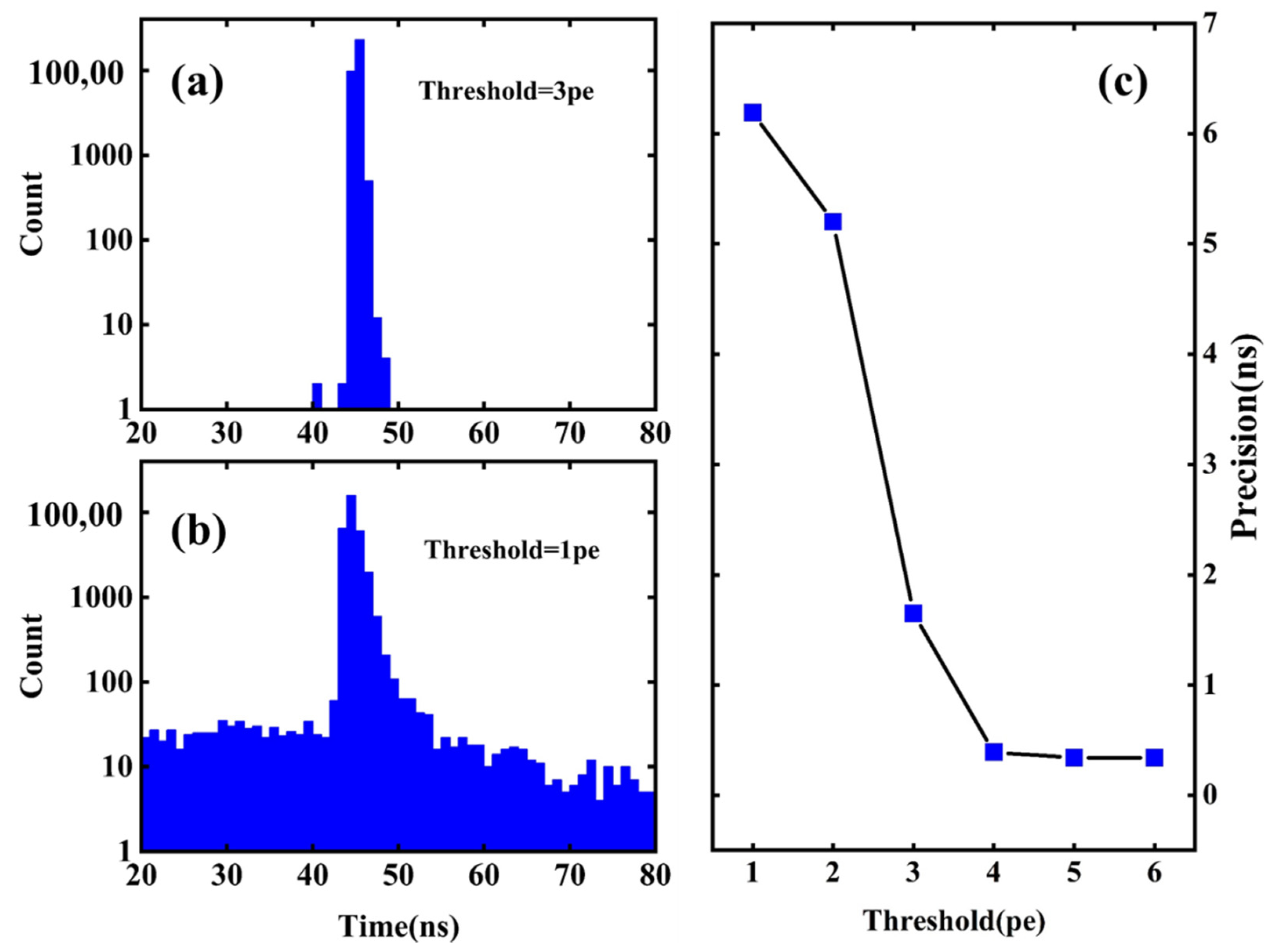
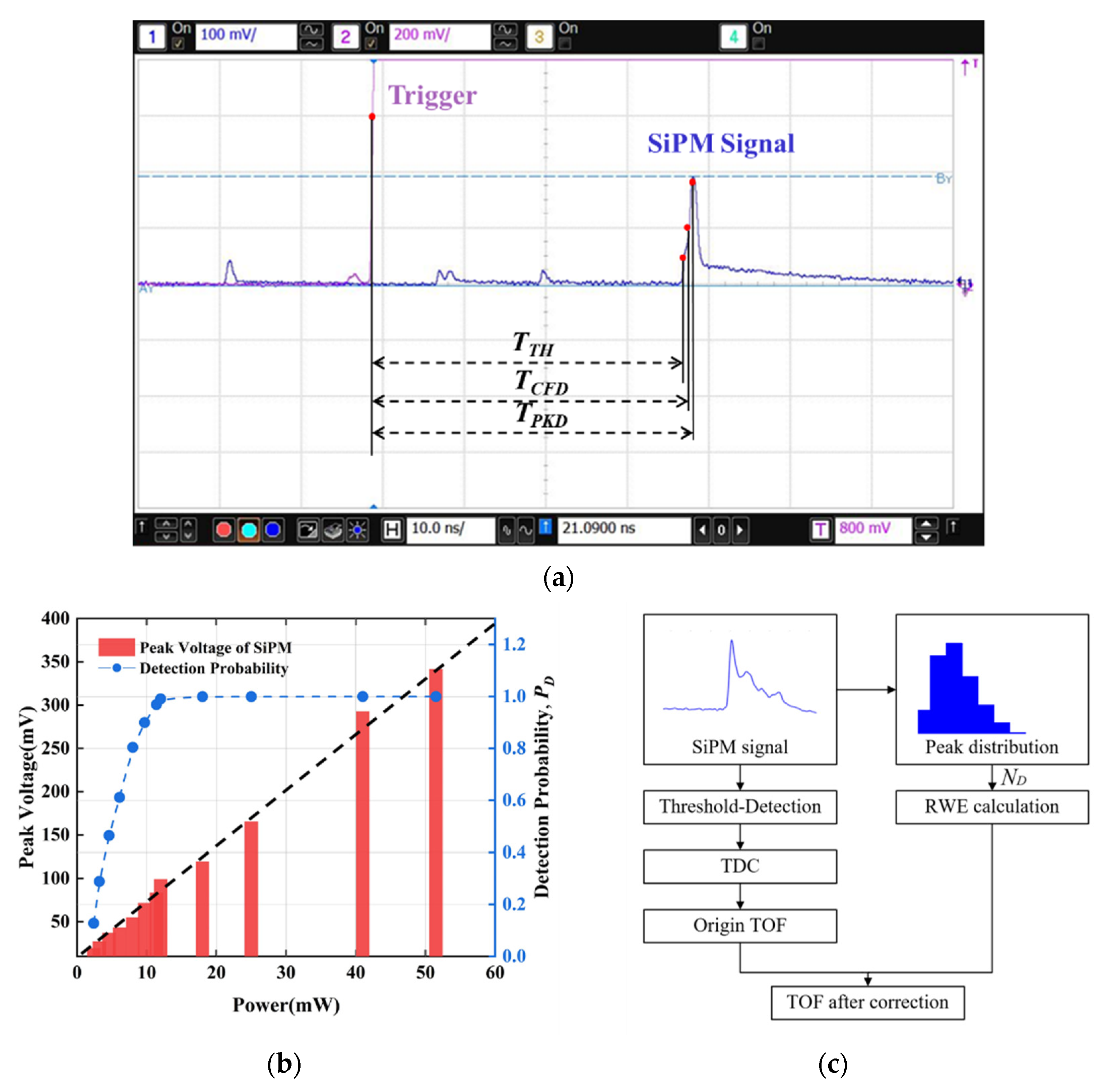
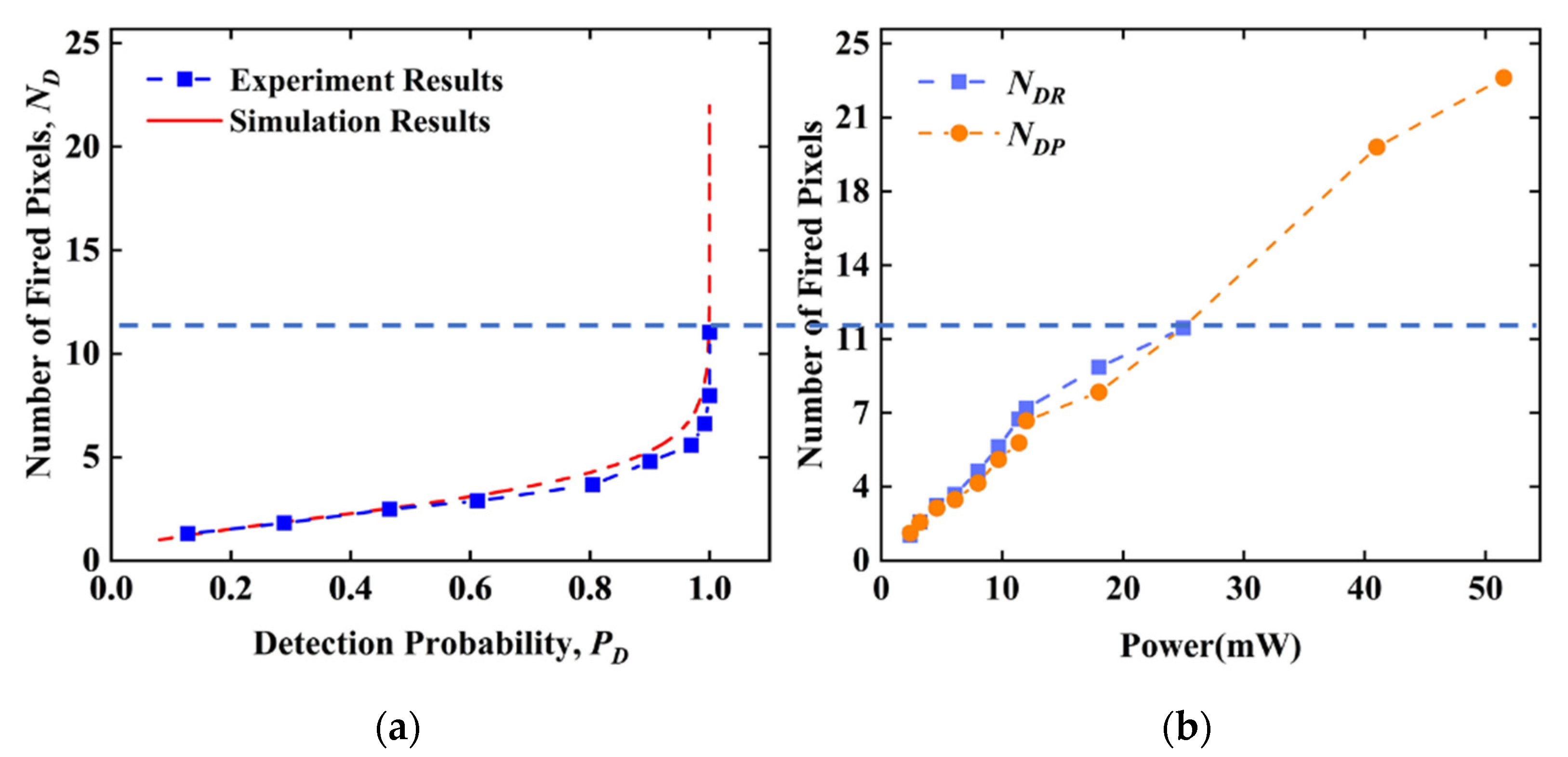
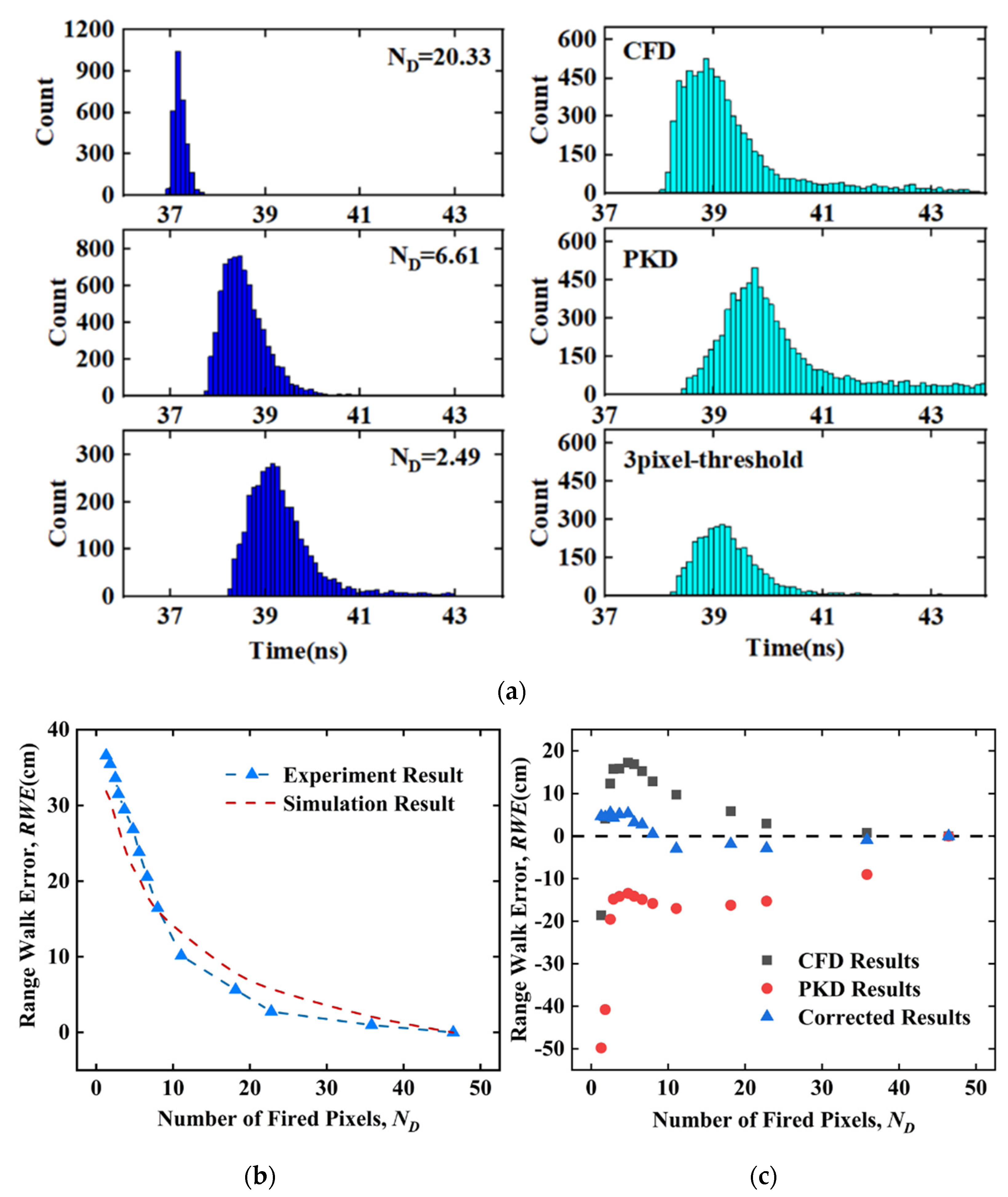
| ND | 2.88 | 4.79 | 7.98 | 18.14 | 33.65 |
| ETH (cm) | 31.52 | 26.86 | 16.45 | 5.65 | 0.97 |
| ECFD (cm) | 15.74 | 17.21 | 12.80 | 5.83 | 0.79 |
| EPKD (cm) | −19.54 | −13.44 | −15.83 | −16.23 | −9.02 |
| ETHC (cm) | 4.34 | 5.30 | 0.51 | −1.85 | −0.91 |
| Precision (cm) | 1.19 | 1.11 | 1.31 | 0.27 | 0.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Tang, Y.; Fu, Z.; Qiu, J.; Liu, K. A Method of Range Walk Error Correction in SiPM LiDAR with Photon Threshold Detection. Photonics 2022, 9, 24. https://doi.org/10.3390/photonics9010024
Yang R, Tang Y, Fu Z, Qiu J, Liu K. A Method of Range Walk Error Correction in SiPM LiDAR with Photon Threshold Detection. Photonics. 2022; 9(1):24. https://doi.org/10.3390/photonics9010024
Chicago/Turabian StyleYang, Runze, Yumei Tang, Zeyu Fu, Jian Qiu, and Kefu Liu. 2022. "A Method of Range Walk Error Correction in SiPM LiDAR with Photon Threshold Detection" Photonics 9, no. 1: 24. https://doi.org/10.3390/photonics9010024
APA StyleYang, R., Tang, Y., Fu, Z., Qiu, J., & Liu, K. (2022). A Method of Range Walk Error Correction in SiPM LiDAR with Photon Threshold Detection. Photonics, 9(1), 24. https://doi.org/10.3390/photonics9010024








