Nonlinear Dynamics of a Single-Mode Semiconductor Laser with Long Delayed Optical Feedback: A Modern Experimental Characterization Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
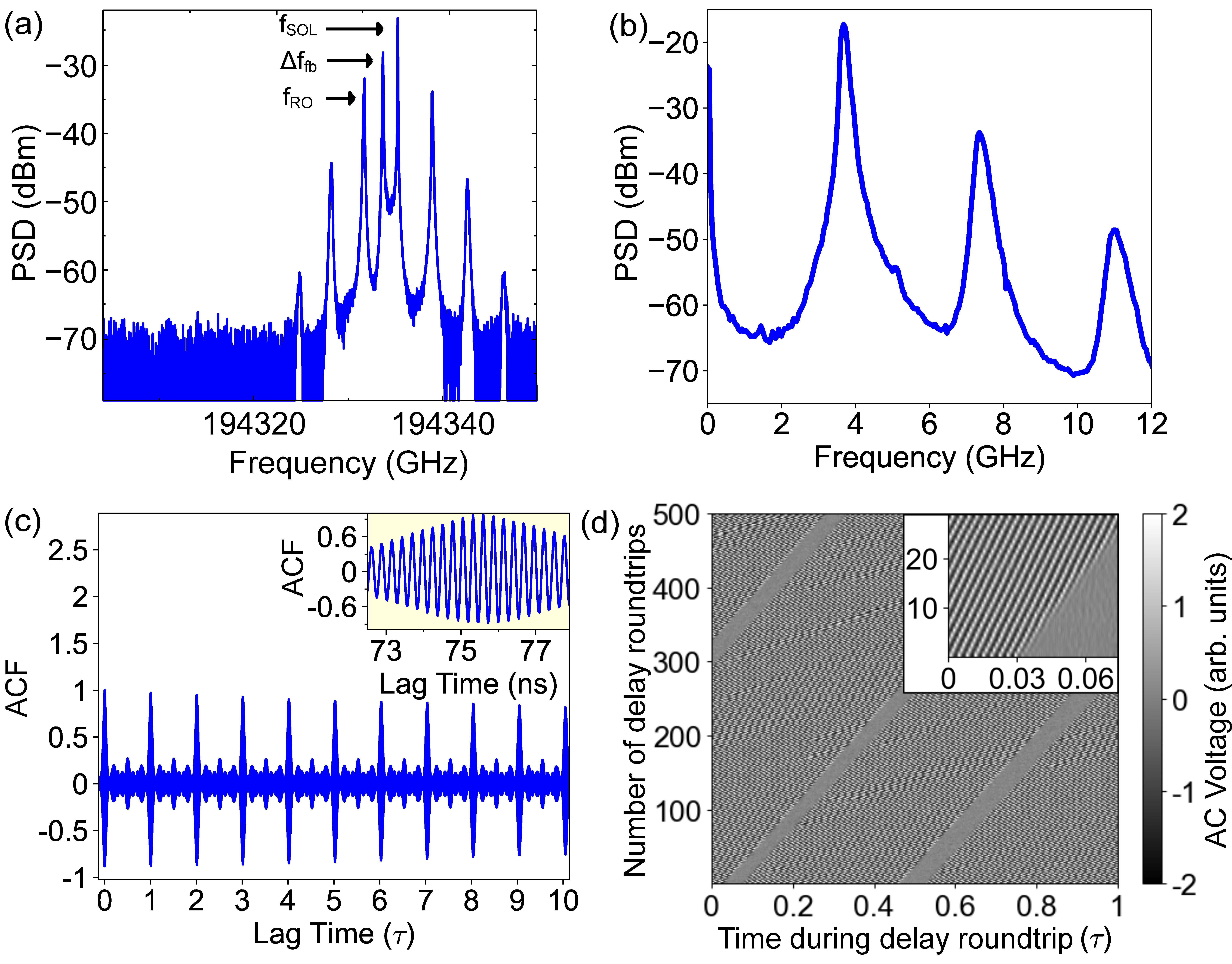
2.2. Spectral Characterization of Feedback-Induced Dynamics
2.3. Temporal Characterization of Feedback-Induced Dynamics
2.4. Theoretical Background
2.4.1. External Cavity Modes
3. Experimental Results: Dynamical Regimes
3.1. Low Feedback Rate
3.2. Intermediate Feedback Rate
3.3. High Feedback Rate
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| ACF | Autocorrelation Function |
| ECM | External Cavity Mode |
| LFF | Low Frequency Fluctuations |
| PSD | Power Spectral Density |
| RF | Radio-Frequency |
| SL | Semiconductor Laser |
References
- Hall, R.; Fenner, G.; Kingsley, J.; Soltys, T.; Carlson, R. Coherent Light Emission From GaAs Junctions. Phys. Rev. Lett. 1962, 9, 366–368. [Google Scholar] [CrossRef]
- Nathan, M.I.; Dumke, W.P.; Burns, G.; Dill, F.H.; Lasher, G. Stimulated Emission of Radiation from GaAs p-n Junctions. Appl. Phys. Lett. 1962, 1, 62. [Google Scholar] [CrossRef]
- Quist, T.M.; Rediker, R.H.; Keyes, R.J.; Krag, W.E.; Lax, B.; McWhorter, A.L.; Zeigler, H.J. Semiconductor Maser of GaAs. Appl. Phys. Lett. 1962, 1, 91. [Google Scholar] [CrossRef]
- Coleman, J.J. The development of the semiconductor laser diode after the first demonstration in 1962. Semicond. Sci. Technol. 2012, 27, 090207. [Google Scholar] [CrossRef]
- Broom, R. Self modulation at gigahertz frequencies of a diode laser coupled to an external cavity. Electron. Lett. 1969, 5, 571. [Google Scholar] [CrossRef]
- Broom, R.; Mohn, E.; Risch, C.; Salathe, R. Microwave self-modulation of a diode laser coupled to an external cavity. IEEE J. Quantum Electron. 1970, 6, 328–334. [Google Scholar] [CrossRef]
- Risch, C.; Voumard, C. Self-pulsation in the output intensity and spectrum of GaAs-AlGaAs cw diode lasers coupled to a frequency-selective external optical cavity. J. Appl. Phys. 1977, 48, 2083. [Google Scholar] [CrossRef]
- Lenstra, D.; Verbeek, B.; den Boef, A. Coherence collapse in single-mode semiconductor lasers due to optical feedback. IEEE J. Quantum Electron. 1985, 21, 674–679. [Google Scholar] [CrossRef]
- Tkach, R.; Chraplyvy, A. Regimes of feedback effects in 1.5-um distributed feedback lasers. J. Light. Technol. 1986, 4, 1655–1661. [Google Scholar] [CrossRef]
- Mørk, J.; Tromborg, B.; Mark, J. Chaos in semiconductor lasers with optical feedback: Theory and experiment. IEEE J. Quantum Electron. 1992, 28, 93–108. [Google Scholar] [CrossRef]
- Heil, T.; Fischer, I.; Elsäßer, W. Stabilization of feedback-induced instabilities in semiconductor lasers. J. Opt. B Quantum Semiclassical Opt. 2000, 2, 413–420. [Google Scholar] [CrossRef] [Green Version]
- Ahlers, V.; Parlitz, U.; Lauterborn, W. Hyperchaotic dynamics and synchronization of external-cavity semiconductor lasers. Phys. Rev. E 1998, 58, 7208. [Google Scholar] [CrossRef] [Green Version]
- Vicente, R.; Daudén, J.; Colet, P.; Toral, R. Analysis and characterization of the hyperchaos generated by a semiconductor laser subject to a delayed feedback loop. IEEE J. Quantum Electron. 2005, 41, 541–548. [Google Scholar] [CrossRef] [Green Version]
- Heil, T.; Fischer, I.; Elsässer, W.; Mulet, J.; Mirasso, C. Chaos Synchronization and Spontaneous Symmetry-Breaking in Symmetrically Delay-Coupled Semiconductor Lasers. Phys. Rev. Lett. 2001, 86, 795–798. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Locquet, A.; Masoller, C.; Mirasso, C.R. Synchronization regimes of optical-feedback-induced chaos in unidirectionally coupled semiconductor lasers. Phys. Rev. E 2002, 65, 056205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Argyris, A.; Syvridis, D.; Larger, L.; Annovazzi-Lodi, V.; Colet, P.; Fischer, I.; García-Ojalvo, J.; Mirasso, C.R.; Pesquera, L.; Shore, K.A. Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 2005, 438, 343–346. [Google Scholar] [CrossRef]
- Uchida, A.; Amano, K.; Inoue, M.; Hirano, K.; Naito, S.; Someya, H.; Oowada, I.; Kurashige, T.; Shiki, M.; Yoshimori, S.; et al. Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photonics 2008, 2, 728–732. [Google Scholar] [CrossRef]
- Peil, M.; Fischer, I.; Elsäßer, W.; Bakić, S.; Damaschke, N.; Tropea, C.; Stry, S.; Sacher, J. Rainbow refractometry with a tailored incoherent semiconductor laser source. Appl. Phys. Lett. 2006, 89, 091106. [Google Scholar] [CrossRef] [Green Version]
- Lin, F.-Y.; Liu, J.-M. Chaotic LIDAR. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 991–997. [Google Scholar] [CrossRef]
- Brunner, D.; Soriano, M.C.; Mirasso, C.R.; Fischer, I. Parallel photonic information processing at gigabyte per second data rates using transient states. Nat. Commun. 2013, 4, 1364. [Google Scholar] [CrossRef] [Green Version]
- Pyragas, K. Continuous control of chaos by self-controlling feedback. Phys. Lett. A 1992, 170, 421–428. [Google Scholar] [CrossRef]
- Stepan, G. Delay effects in brain dynamics. Introduction. Philos. Trans. Ser. Math. Phys. Eng. 2009, 367, 1059–1062. [Google Scholar]
- Orosz, G.; Wilson, R.E.; Szalai, R.; Stépán, G. Exciting traffic jams: Nonlinear phenomena behind traffic jam formation on highways. Phys. Rev. E 2009, 80, 046205. [Google Scholar] [CrossRef] [PubMed]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Elowitz, M.B.; Leibler, S. A synthetic oscillatory network of transcriptional regulators. Nature 2000, 403, 335–338. [Google Scholar] [CrossRef]
- Chen, L.; Aihara, K. Stability of genetic regulatory networks with time delay. IEEE Trans. Circuits Syst. Fundam. Appl. 2002, 49, 602–608. [Google Scholar] [CrossRef]
- Yeung, M.; Strogatz, S. Time Delay in the Kuramoto Model of Coupled Oscillators. Phys. Rev. Lett. 1999, 82, 648–651. [Google Scholar] [CrossRef] [Green Version]
- Keuninckx, L.; Soriano, M.C.; Fischer, I.; Mirasso, C.R.; Nguimdo, R.M.; van der Sande, G. Encryption key distribution via chaos synchronization. Sci. Rep. 2017, 7, 43428. [Google Scholar] [CrossRef] [Green Version]
- Soriano, M.C.; García-Ojalvo, J.; Mirasso, C.R.; Fischer, I. Complex photonics: Dynamics and applications of delay-coupled semiconductors lasers. Rev. Mod. Phys. 2013, 85, 421–470. [Google Scholar] [CrossRef] [Green Version]
- Kelly, B.; Phelan, R.; Jones, D.; Herbert, C.; O’Carroll, J.; Rensing, M.; Wendelboe, J.; Watts, C.; Kaszubowska-Anandarajah, A.; Guignard, C.; et al. Discrete mode laser diodes with very narrow linewidth emission. Electron. Lett. 2007, 43, 1282. [Google Scholar] [CrossRef] [Green Version]
- Brunner, D.; Luna, R.; Latorre, A.D.i.; Porte, X.; Fischer, I. Semiconductor laser linewidth reduction by six orders of magnitude via delayed optical feedback. Opt. Lett. 2017, 42, 163–166. [Google Scholar] [CrossRef]
- Baili, G.; Alouini, M.; Malherbe, T.; Dolfi, D.; Sagnes, I.; Bretenaker, F. Direct observation of the class-B to class-A transition in the dynamical behavior of a semiconductor laser. Europhys. Lett. 2009, 87, 44005. [Google Scholar] [CrossRef] [Green Version]
- Porte, X.; D’Huys, O.; Jüngling, T.; Brunner, D.; Soriano, M.C.; Fischer, I. Autocorrelation properties of chaotic delay dynamical systems: A study on semiconductor lasers. Phys. Rev. E 2014, 90, 052911. [Google Scholar] [CrossRef] [Green Version]
- Henry, C. Theory of the linewidth of semiconductor lasers. IEEE J. Quantum Electron. 1982, 18, 259–264. [Google Scholar] [CrossRef]
- Fischer, I.; van Tartwijk, G.; Levine, A.; Elsässer, W.; Göbel, E.; Lenstra, D. Fast Pulsing and Chaotic Itinerancy with a Drift in the Coherence Collapse of Semiconductor Lasers. Phys. Rev. Lett. 1996, 76, 220–223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arecchi, F.; Giacomelli, G.; Lapucci, A.; Meucci, R. Two-dimensional representation of a delayed dynamical system. Phys. Rev. A 1992, 45, R4225–R4228. [Google Scholar] [CrossRef]
- Masoller, C. Spatiotemporal dynamics in the coherence collapsed regime of semiconductor lasers with optical feedback. Chaos 1997, 7, 455–462. [Google Scholar] [CrossRef] [PubMed]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Petermann, K. External optical feedback phenomena in semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 1995, 1, 480–489. [Google Scholar] [CrossRef]
- Sano, T. Antimode dynamics and chaotic itinerancy in the coherence collapse of semiconductor lasers with optical feedback. Phys. Rev. A 1994, 50, 2719–2726. [Google Scholar] [CrossRef] [PubMed]
- Henry, C.; Kazarinov, R. Instability of semiconductor lasers due to optical feedback from distant reflectors. IEEE J. Quantum Electron. 1986, 22, 294–301. [Google Scholar] [CrossRef]
- Porte, X.; Soriano, M.C.; Fischer, I. Similarity properties in the dynamics of delayed-feedback semiconductor lasers. Phys. Rev. A 2014, 89, 023822. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.; Li, N.; Locquet, A.; Citrin, D.S. Experimental bifurcation-cascade diagram of an external-cavity semiconductor laser. Opt. Express 2014, 22, 2348–2357. [Google Scholar] [CrossRef]
- Mørk, J.; Mark, J.; Tromborg, B. Route to chaos and competition between relaxation oscillations for a semiconductor laser with optical feedback. Phys. Rev. Lett. 1990, 65, 1999–2002. [Google Scholar] [CrossRef] [PubMed]
- Masoller, C.; Abraham, N.B. Stability and dynamical properties of the coexisting attractors of an external-cavity semiconductor laser. Phys. Rev. A 1998, 57, 1313–1322. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.X.; Ruan, J.; Zhang, L.; Zhuang, J.P.; Chan, S.C. Stable-unstable switching dynamics in semiconductor lasers with external cavities. Phys. Rev. A 2021, 103, 053524. [Google Scholar] [CrossRef]
- Heiligenthal, S.; Dahms, T.; Yanchuk, S.; Jüngling, T.; Flunkert, V.; Kanter, I.; Schöll, E.; Kinzel, W. Strong and Weak Chaos in Nonlinear Networks with Time-Delayed Couplings. Phys. Rev. Lett. 2011, 107, 234102. [Google Scholar] [CrossRef]
- Heiligenthal, S.; Jüngling, T.; D’Huys, O.; Arroyo-Almanza, D.A.; Soriano, M.C.; Fischer, I.; Kanter, I.; Kinzel, W. Strong and weak chaos in networks of semiconductor lasers with time-delayed couplings. Phys. Rev. E 2013, 88, 012902. [Google Scholar] [CrossRef] [Green Version]
- Mørk, J.; Tromborg, B.; Christiansen, P.L. Bistability and low-frequency fluctuations in semiconductor lasers with optical feedback: A theoretical analysis. IEEE J. Quantum Electron. 1988, 24, 123–133. [Google Scholar] [CrossRef] [Green Version]
- Sukow, D.W.; Gardner, J.R.; Gauthier, D.J. Statistics of power-dropout events in semiconductor lasers with time-delayed optical feedback. Phys. Rev. A 1997, 56, R3370. [Google Scholar] [CrossRef]
- Heil, T.; Fischer, I.; Elsäßer, W. Coexistence of low-frequency fluctuations and stable emission on a single high-gain mode in semiconductor lasers with external optical feedback. Phys. Rev. A 1998, 58, R2672–R2675. [Google Scholar] [CrossRef] [Green Version]
- Brunner, D.; Porte, X.; Soriano, M.C.; Fischer, I. Real-time frequency dynamics and high-resolution spectra of a semiconductor laser with delayed feedback. Sci. Rep. 2012, 2, 732. [Google Scholar] [CrossRef] [Green Version]
- Brunner, D.; Soriano, M.C.; Porte, X.; Fischer, I. Experimental Phase-Space Tomography of Semiconductor Laser Dynamics. Phys. Rev. Lett. 2015, 115, 053901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martínez-Llinàs, J.; Porte, X.; Soriano, M.C.; Colet, P.; Fischer, I. Dynamical properties induced by state-dependent delays in photonic systems. Nat. Commun. 2015, 6, 7425. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yanchuk, S.; Giacomelli, G. Pattern formation in systems with multiple delayed feedbacks. Phys. Rev. Lett. 2014, 112, 174103. [Google Scholar] [CrossRef] [Green Version]
- Van der Sande, G.; Brunner, D.; Soriano, M.C. Advances in photonic reservoir computing. Nanophotonics 2017, 6, 561–576. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porte, X.; Brunner, D.; Fischer, I.; Soriano, M.C. Nonlinear Dynamics of a Single-Mode Semiconductor Laser with Long Delayed Optical Feedback: A Modern Experimental Characterization Approach. Photonics 2022, 9, 47. https://doi.org/10.3390/photonics9010047
Porte X, Brunner D, Fischer I, Soriano MC. Nonlinear Dynamics of a Single-Mode Semiconductor Laser with Long Delayed Optical Feedback: A Modern Experimental Characterization Approach. Photonics. 2022; 9(1):47. https://doi.org/10.3390/photonics9010047
Chicago/Turabian StylePorte, Xavier, Daniel Brunner, Ingo Fischer, and Miguel C. Soriano. 2022. "Nonlinear Dynamics of a Single-Mode Semiconductor Laser with Long Delayed Optical Feedback: A Modern Experimental Characterization Approach" Photonics 9, no. 1: 47. https://doi.org/10.3390/photonics9010047
APA StylePorte, X., Brunner, D., Fischer, I., & Soriano, M. C. (2022). Nonlinear Dynamics of a Single-Mode Semiconductor Laser with Long Delayed Optical Feedback: A Modern Experimental Characterization Approach. Photonics, 9(1), 47. https://doi.org/10.3390/photonics9010047





