Measurement of the Attenuation Coefficient in Fresh Water Using the Adjacent Frame Difference Method
Abstract
:1. Introduction
2. Methods
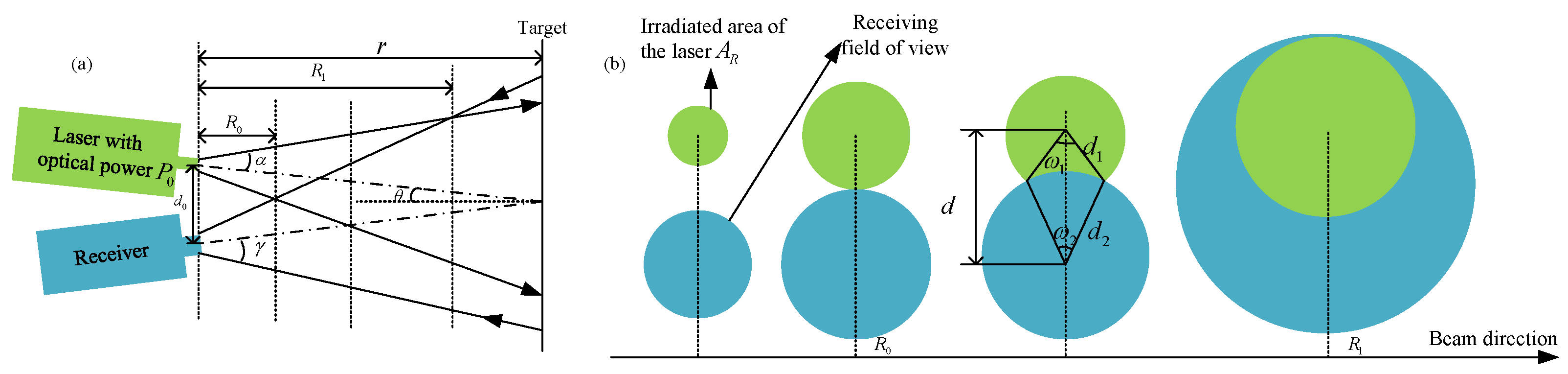
2.1. Backscattering Model in the Water
2.2. Obtaining the Backscattering Intensity by the AFD Method
3. Experiments
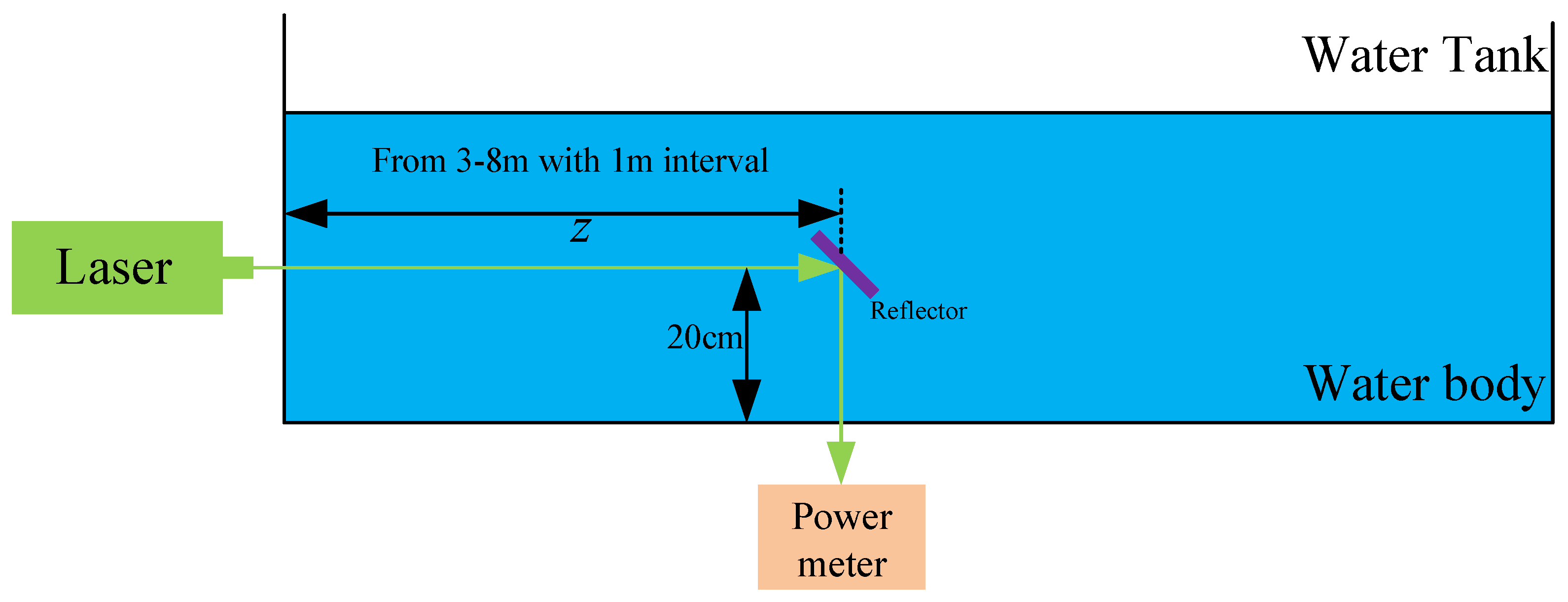
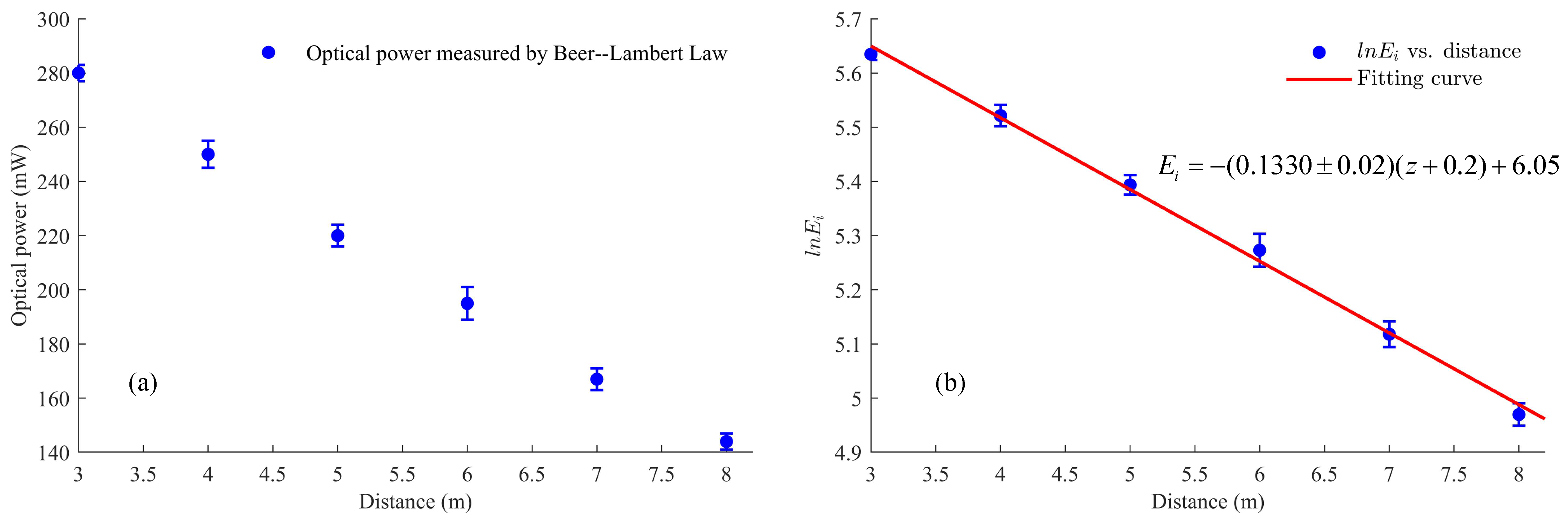
3.1. Measurement of the Water Attenuation Coefficient by the Beer–Lambert Law
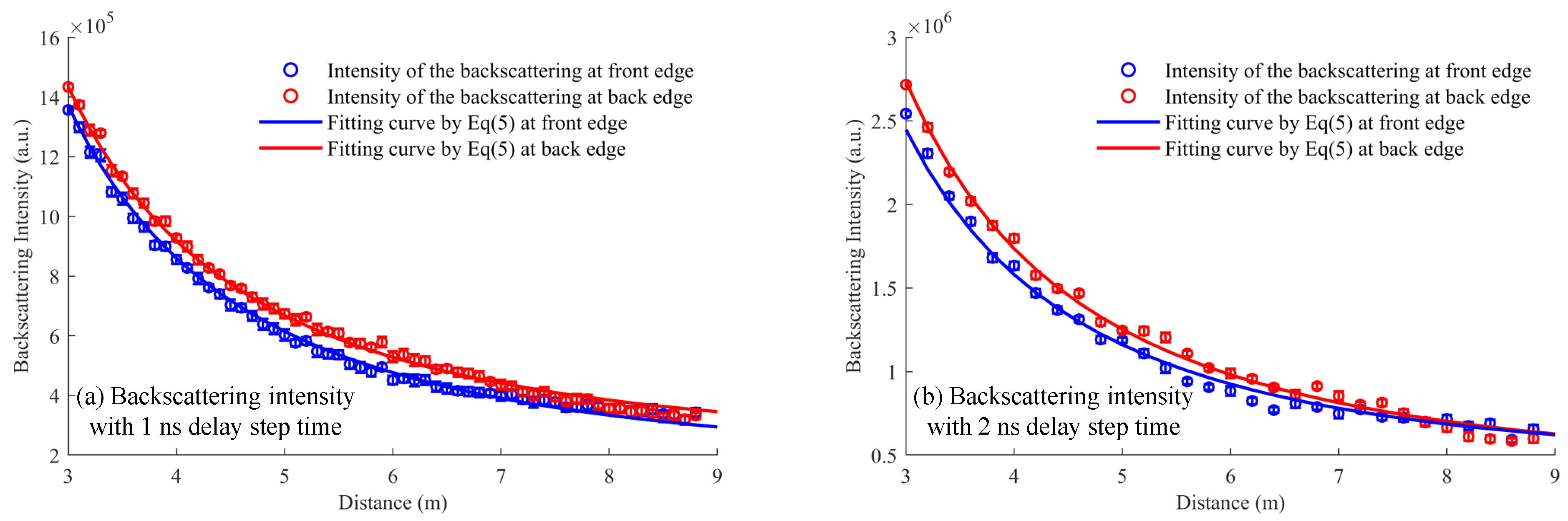
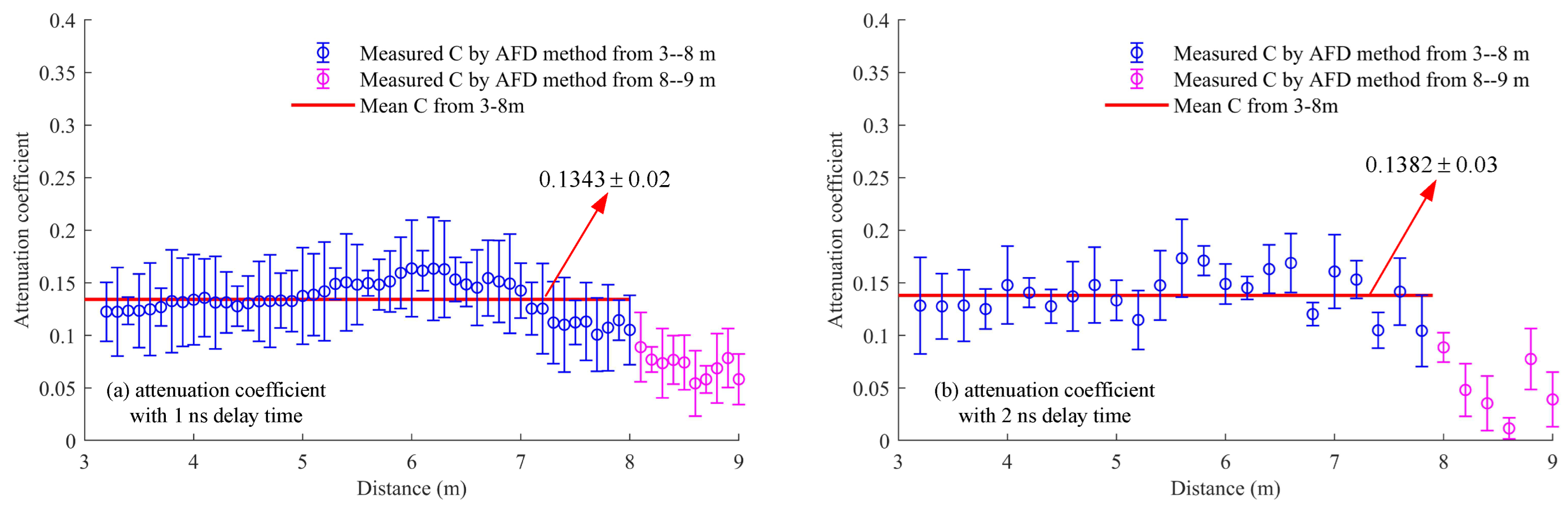
3.2. Experimental Measurement of Water Attenuation Coefficient by AFD Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFD | Adjacent frame difference |
| 3D | Three-dimensional |
| ICCD | Intensified-charge-coupled device |
| SNR | Signal-to-noise ratio |
References
- Babin, M.; Roesler, C.S.; Cullen, J.J. Real-Time Coastal Observing Systems for Marine Ecosystem Dynamics and Harmful Algal Blooms: Theory, Instrumentation and Modelling; Unesco: London, UK, 2008. [Google Scholar]
- Ingles, J.; Louw, T.M.; Booysen, M. Water quality assessment using a portable UV optical absorbance nitrate sensor with a scintillator and smartphone camera. Water SA 2021, 47, 135–140. [Google Scholar]
- Min, R.; Liu, Z.; Pereira, L.; Yang, C.; Sui, Q.; Marques, C. Optical fiber sensing for marine environment and marine structural health monitoring: A review. Opt. Laser Technol. 2021, 140, 107082. [Google Scholar] [CrossRef]
- Gasowski, R.A.; Pawlak, B. Light attenuation in waters of the Oder River and Pomeranian Bay. In Proceedings of the 13th Polish-Czech-Slovak Conference on Wave and Quantum Aspects of Contemporary Optics. International Society for Optics and Photonics, Krzyżowa, Poland, 9–13 September 2002; Volume 5259, pp. 372–378. [Google Scholar]
- Sullivan, J.M.; Donaghay, P.L.; Rines, J.E. Coastal thin layer dynamics: Consequences to biology and optics. Cont. Shelf Res. 2010, 30, 50–65. [Google Scholar] [CrossRef]
- Chang, N.; Luo, L.; Wang, X.C.; Song, J.; Han, J.; Ao, D. A novel index for assessing the water quality of urban landscape lakes based on water transparency. Sci. Total Environ. 2020, 735, 139351. [Google Scholar] [CrossRef]
- Bardaji, R.; Sánchez, A.M.; Simon, C.; Wernand, M.R.; Piera, J. Estimating the underwater diffuse attenuation coefficient with a low-cost instrument: The KdUINO DIY buoy. Sensors 2016, 16, 373. [Google Scholar] [CrossRef]
- Ata, Y.; Korotkova, O. Absorption, scattering, and optical turbulence in natural waters. Appl. Opt. 2022, 61, 4404–4411. [Google Scholar] [CrossRef]
- Wang, F.; Umehara, A.; Nakai, S.; Nishijima, W. Distribution of region-specific background Secchi depth in Tokyo Bay and Ise Bay, Japan. Ecol. Indic. 2019, 98, 397–408. [Google Scholar] [CrossRef]
- Weiskerger, C.J.; Rowe, M.D.; Stow, C.A.; Stuart, D.; Johengen, T. Application of the Beer–Lambert model to attenuation of photosynthetically active radiation in a shallow, eutrophic lake. Water Resour. Res. 2018, 54, 8952–8962. [Google Scholar] [CrossRef]
- Bazzani, M.; Cecchi, G.; Pantani, L.; Raimondi, V. Lidar measurement of light attenuation in water. In Proceedings of the Earth Surface Remote Sensing II. SPIE, Barcelona, Spain, 21–24 September 1998; Volume 3496, pp. 223–227. [Google Scholar]
- Oellker, J.; Richter, A.; Dinter, T.; Rozanov, V.V. Global diffuse attenuation coefficient derived from vibrational Raman scattering detected in hyperspectral backscattered satellite spectra. Opt. Express 2019, 27, A829–A855. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, M.; Shi, J.; Zhao, L.; Chen, X.; Jing, H.; Liu, D. Real time measurement of the attenuation coefficient of water in open ocean based on stimulated Brillouin scattering. Appl. Phys. B 2008, 91, 381–385. [Google Scholar] [CrossRef]
- Shi, J.; Xu, J.; Guo, Y.; Luo, N.; Li, S.; He, X. Dependence of stimulated Brillouin scattering in water on temperature, pressure, and attenuation coefficient. Phys. Rev. Appl. 2021, 15, 054024. [Google Scholar] [CrossRef]
- Hu, Y.; Behrenfeld, M.; Hostetler, C.; Pelon, J.; Trepte, C.; Hair, J.; Slade, W.; Cetinic, I.; Vaughan, M.; Lu, X.; et al. Ocean lidar measurements of beam attenuation and a roadmap to accurate phytoplankton biomass estimates. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2016; Volume 119, p. 22003. [Google Scholar]
- Montes-Hugo, M.A.; Vuorenkoski, A.K.; Dalgleish, F.R.; Ouyang, B. Weibull approximation of LiDAR waveforms for estimating the beam attenuation coefficient. Opt. Express 2016, 24, 22670–22681. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Lee, Z.; Ondrusek, M.; Liu, X. Hyperspectral absorption and backscattering coefficients of bulk water retrieved from a combination of remote-sensing reflectance and attenuation coefficient. Opt. Express 2018, 26, A157–A177. [Google Scholar] [CrossRef] [PubMed]
- Maffione, R.A.; Dana, D.R. Instruments and methods for measuring the backward-scattering coefficient of ocean waters. Appl. Opt. 1997, 36, 6057–6067. [Google Scholar] [CrossRef] [PubMed]
- Kirk, J.T. The vertical attenuation of irradiance as a function of the optical properties of the water. Limnol. Oceanogr. 2003, 48, 9–17. [Google Scholar] [CrossRef]
- Green, R.E.; Sosik, H.M. Analysis of apparent optical properties and ocean color models using measurements of seawater constituents in New England continental shelf surface waters. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Maciel, D.A.; Barbosa, C.C.F.; de Moraes Novo, E.M.L.; Cherukuru, N.; Martins, V.S.; Flores Júnior, R.; Jorge, D.S.; Sander de Carvalho, L.A.; Carlos, F.M. Mapping of diffuse attenuation coefficient in optically complex waters of amazon floodplain lakes. ISPRS J. Photogramm. Remote Sens. 2020, 170, 72–87. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, J.Y.; An, K.G. Trophic responses of the Asian reservoir to long-term seasonal and interannual dynamic monsoon. Water 2020, 12, 2066. [Google Scholar] [CrossRef]
- Tian, Z.; Yang, G.; Zhang, Y.; Cui, Z.; Bi, Z. A range-gated imaging flash Lidar based on the adjacent frame difference method. Opt. Lasers Eng. 2021, 141, 106558. [Google Scholar] [CrossRef]
- Harsdorf, S.; Reuter, R. Laser remote sensing in highly turbid waters: Validity of the lidar equation. In Proceedings of the Environmental Sensing and Applications, Munich, Germany, 14–17 June 1999; Volume 3821, pp. 369–377. [Google Scholar]
- Katsev, I.L.; Zege, E.P.; Prikhach, A.S.; Polonsky, I.N. Efficient technique to determine backscattered light power for various atmospheric and oceanic sounding and imaging systems. JOSA A 1997, 14, 1338–1346. [Google Scholar] [CrossRef]
- Maffione, R.A.; Dana, D.R.; Honey, R.C. Instrument for underwater measurement of optical backscatter. In Proceedings of the Underwater Imaging, Photography, and Visibility, San Diego, CA, USA, 23 July 1991; Volume 1537, pp. 173–184. [Google Scholar]
- Mishra, R.; Pillai, A.; Sheshadri, M.; Sarma, C.S. Airborne electro-optical sensor: Performance predictions and design considerations. In Proceedings of the Acquisition, Tracking, and Pointing V, Orlando, FL, USA, 3–5 April 1991; Volume 1482, pp. 138–145. [Google Scholar]


| 20 cm | 1 m | 1.5 m | 30 ns | 20 ns |
| Distance (m) | Beer–Lambert law | AFD Method | ||
|---|---|---|---|---|
| C | Relative Error | C | Relative Error | |
| 3 to 4 | 0.1133 | 0.1278 | ||
| 3 to 5 | 0.1206 | 0.1303 | ||
| 3 to 6 | 0.1152 | 0.1376 | ||
| 3 to 7 | 0.1262 | 0.1406 | ||
| 3 to 8 | 0.1330 | 0.1343 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Tian, Z.; Bi, Z.; Cui, Z.; Sun, F.; Liu, Q. Measurement of the Attenuation Coefficient in Fresh Water Using the Adjacent Frame Difference Method. Photonics 2022, 9, 713. https://doi.org/10.3390/photonics9100713
Yang G, Tian Z, Bi Z, Cui Z, Sun F, Liu Q. Measurement of the Attenuation Coefficient in Fresh Water Using the Adjacent Frame Difference Method. Photonics. 2022; 9(10):713. https://doi.org/10.3390/photonics9100713
Chicago/Turabian StyleYang, Gang, Zhaoshuo Tian, Zongjie Bi, Zihao Cui, Fenghao Sun, and Qingcao Liu. 2022. "Measurement of the Attenuation Coefficient in Fresh Water Using the Adjacent Frame Difference Method" Photonics 9, no. 10: 713. https://doi.org/10.3390/photonics9100713
APA StyleYang, G., Tian, Z., Bi, Z., Cui, Z., Sun, F., & Liu, Q. (2022). Measurement of the Attenuation Coefficient in Fresh Water Using the Adjacent Frame Difference Method. Photonics, 9(10), 713. https://doi.org/10.3390/photonics9100713






