Optical-Frequency-Comb Generation Based on Single-Tone Modulation and Four-Wave Mixing Effect in One Single Semiconductor Optical Amplifier
Abstract
1. Introduction
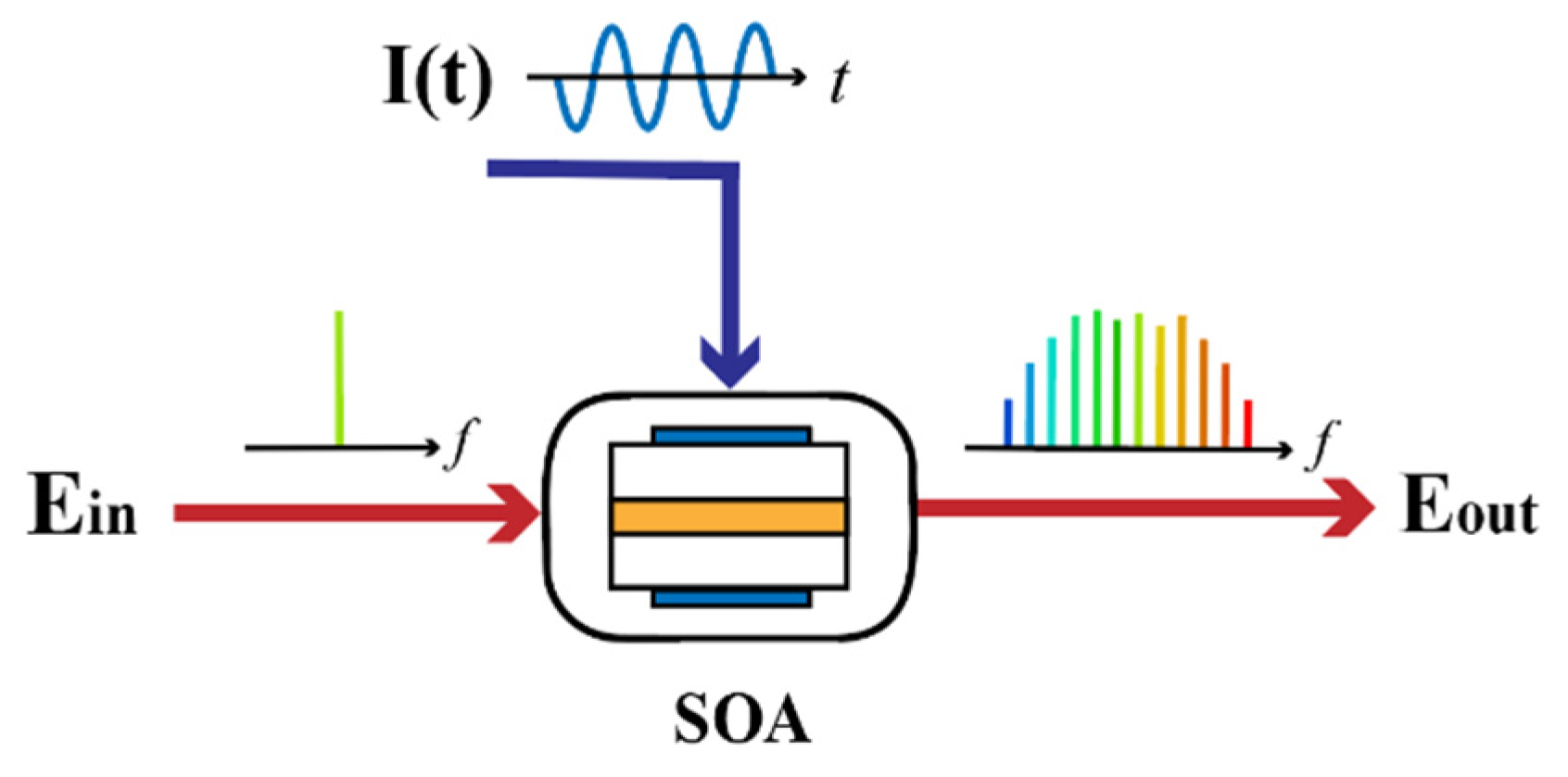
2. Operation Principle
3. Broad-Band Dynamic Model
- A.
- The traveling-wave equations.
- B.
- The traveling-wave equations for the ASE spectrum.
- C.
- The carrier-density-rate equation.
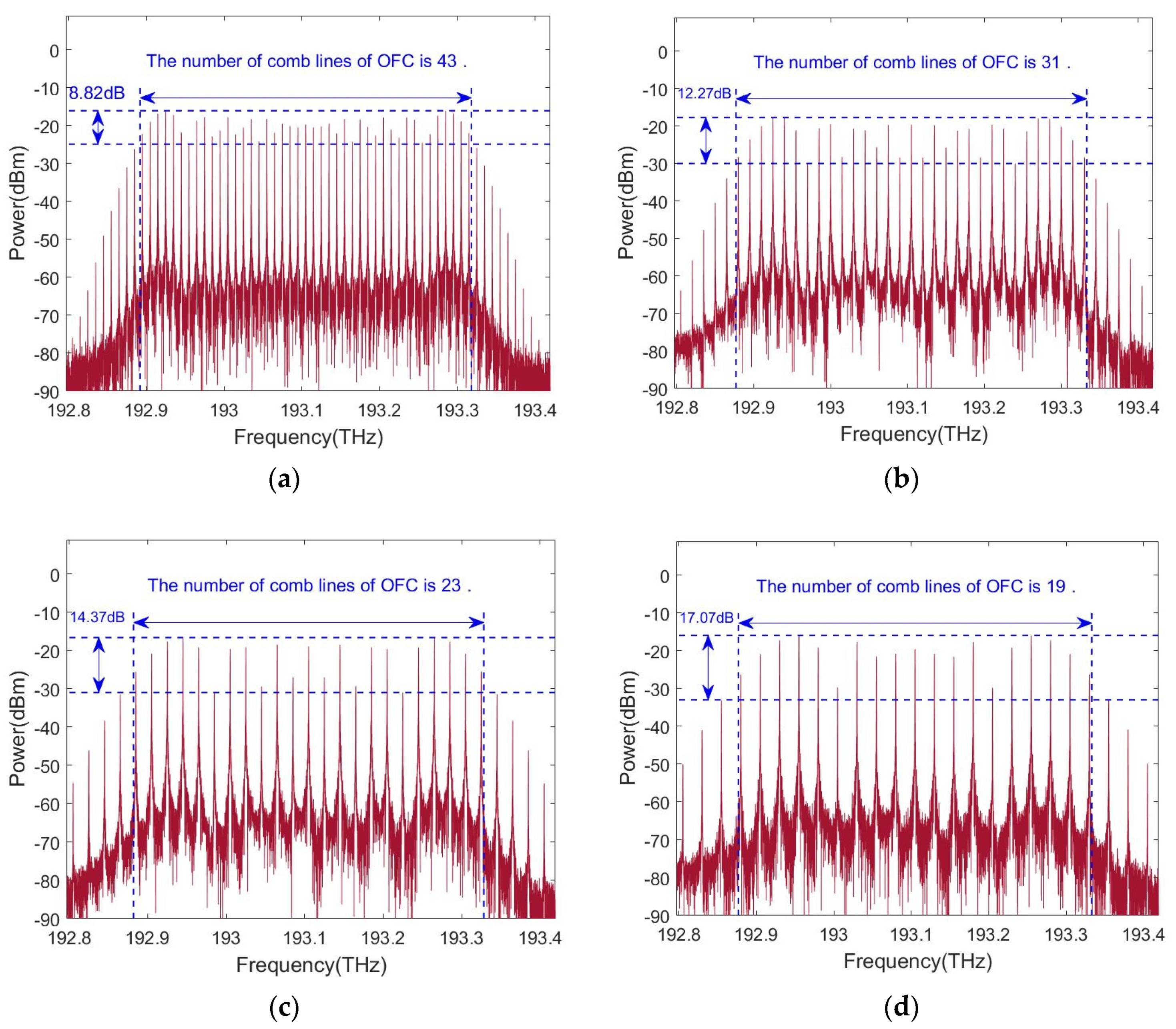
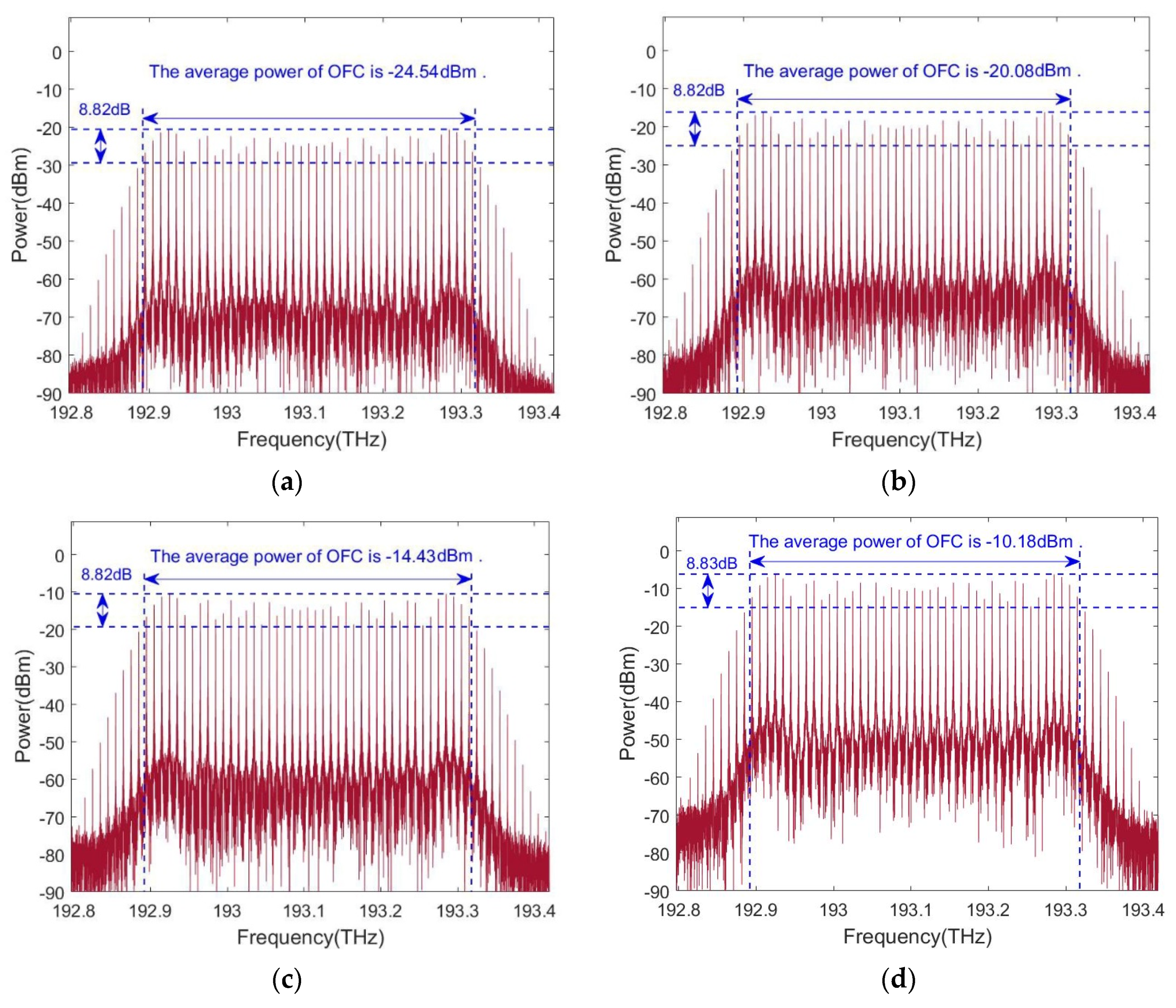
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rutkowski, L.; Masłowski, P.; Johansson, A.C.; Khodabakhsh, A.; Foltynowicz, A. Optical frequency comb Fourier transform spectroscopy with sub-nominal resolution and precision beyond the Voigt profile. J. Quant. Spectrosc. Radiat. Transf. 2018, 204, 63–73. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, H.; Chen, Y.; Li, P. Full-duplex WDM-RoF system based on OFC with dual frequency microwave signal generation and wavelength reuse. Opt. Fiber Technol. 2020, 58, 102252. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, P.; Chen, L.; Huang, C.; Liu, D.; Jiang, S. Optical fiber strain sensor using fiber resonator based on frequency comb Vernier spectroscopy. Opt. Lett. 2012, 37, 2622–2624. [Google Scholar] [CrossRef] [PubMed]
- Alshaykh, M.S.; McKinney, J.D.; Weiner, A.M. Radio-Frequency Signal Processing Using Optical Frequency Combs. IEEE Photon- Technol. Lett. 2019, 31, 1874–1877. [Google Scholar] [CrossRef]
- He, X.; Zhang, P.; Zhang, Y.; Lin, Q.; Guo, H.; Hou, L.; Wang, K. Wavelength-Tunable Ultra-Stable Optical Frequency Comb Based on All-Polarization-Maintaining Fiber Laser. Front. Phys. 2020, 8, 226. [Google Scholar] [CrossRef]
- Sharma, V.; Singh, S.; Lovkesh; Anashkina, E.A.; Andrianov, A.V. Demonstration of optical frequency comb generation using four-wave mixing in highly nonlinear fiber. Optik 2021, 241, 166948. [Google Scholar] [CrossRef]
- Amiune, N.; Puzyrev, D.N.; Pankratov, V.V.; Skryabin, D.V.; Buse, K.; Breunig, I. Optical-parametric-oscillation-based χ(2) frequency comb in a lithium niobate microresonator. Opt. Express 2021, 29, 41378. [Google Scholar] [CrossRef]
- Puzyrev, D.N.; Pankratov, V.V.; Villois, A.; Skryabin, D.V. Bright soliton frequency combs and dressed states in χ(2) microresonators. Phys. Rev. A 2021, 104, 013520. [Google Scholar] [CrossRef]
- Stefszky, M.; Ulvila, V.; Abdallah, Z.; Silberhorn, C.; Vainio, M. Towards optical-frequency-comb generation in continuous-wave-pumped titanium-indiffused lithium-niobate waveguide resonators. Phys. Rev. A 2018, 98, 053850. [Google Scholar] [CrossRef]
- Ullah, R.; Ullah, S.; Khan, G.Z.; Dai, Y.; Yin, F.; Zhou, Y.; Li, J.; Xu, K. Ultrawide and tunable self-oscillating optical frequency comb generator based on an optoelectronic oscillator. Results Phys. 2021, 22, 103849. [Google Scholar] [CrossRef]
- Francis, H.; Zhang, X.-D.; Chen, S.; Yu, J.-W.; Che, K.-J.; Hopkinson, M.; Jin, C.-Y. Optical Frequency Comb Generation via Cascaded Intensity and Phase Photonic Crystal Modulators. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1–9. [Google Scholar] [CrossRef]
- Yu, Y.; Huang, L.; Xiong, M.; Tian, P.; Huang, D. Enhancement of gain recovery rate and cross-gain modulation bandwidth using two-electrode quantum-dot semiconductor optical amplifier. J. Opt. Soc. Am. B 2010, 27, 2211–2217. [Google Scholar]
- Huang, L.; Huang, D.; Chen, J.; Liu, D.; Zhang, X. Analysis of a semiconductor optical amplifier with polarization-insensitive gain and polarization-insensitive phase modulation. Semicond. Sci. Technol. 2006, 21, 1643–1650. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, X.; Fu, S.; Xu, J.; Shum, P.; Huang, D. Ultrafast All-Optical Signal Processing Based on Single Semiconductor Optical Amplifier and Optical Filtering. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 770–778. [Google Scholar] [CrossRef]
- Simos, H.; Bogris, A.; Syvridis, D. Investigation of a 2R All-Optical Regenerator Based on Four-Wave Mixing in a Semiconductor Optical Amplifier. J. Light. Technol. 2004, 22, 595–604. [Google Scholar] [CrossRef]
- Lakshmijayasimha, P.D.; Kaszubowska-Anandarajah, A.; Martin, E.P.; Landais, P.; Anandarajah, P.M. Expansion and phase correlation of a wavelength tunable gain-switched optical frequency comb. Opt. Express 2019, 27, 16560–16570. [Google Scholar] [CrossRef]
- Wei, J.L.; Hamié, A.; Gidding, R.P.; Hugues-Salas, E.; Zheng, X.; Mansoor, S.; Tang, J.M. Adaptively modulated optical OFDM modems utilizing RSOAs as intensity modulators in IMDD SMF transmission systems. Opt. Express 2010, 18, 8556. [Google Scholar] [CrossRef]
- Thomas, E.; Rizouu, Z.V. Semiconductor optical amplifier direct modulation with double-stage birefringent fiber loop. Appl. Phys. B 2016, 122, 158. [Google Scholar]
- Connelly, M. Wideband semiconductor optical amplifier steady-state numerical model. IEEE J. Quantum Electron. 2001, 37, 439–447. [Google Scholar] [CrossRef]
- Pei, L.; Huang, D.-X.; Zhang, X.-L.; Chen, J.; Huang, L.-R. Theoretical analysis of tunable wavelength conversion based on FWM in a semiconductor fiber ring laser. IEEE J. Quantum Electron. 2005, 41, 581–588. [Google Scholar] [CrossRef]
- Talli, G.; Adams, M.J. Amplified spontaneous emission in semiconductor optical amplifiers: Modeling and experiments. Opt. Commun. 2003, 218, 161–166. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Z.; Huang, L. Optical-Frequency-Comb Generation Based on Single-Tone Modulation and Four-Wave Mixing Effect in One Single Semiconductor Optical Amplifier. Photonics 2022, 9, 746. https://doi.org/10.3390/photonics9100746
Tan Z, Huang L. Optical-Frequency-Comb Generation Based on Single-Tone Modulation and Four-Wave Mixing Effect in One Single Semiconductor Optical Amplifier. Photonics. 2022; 9(10):746. https://doi.org/10.3390/photonics9100746
Chicago/Turabian StyleTan, Zeyu, and Lirong Huang. 2022. "Optical-Frequency-Comb Generation Based on Single-Tone Modulation and Four-Wave Mixing Effect in One Single Semiconductor Optical Amplifier" Photonics 9, no. 10: 746. https://doi.org/10.3390/photonics9100746
APA StyleTan, Z., & Huang, L. (2022). Optical-Frequency-Comb Generation Based on Single-Tone Modulation and Four-Wave Mixing Effect in One Single Semiconductor Optical Amplifier. Photonics, 9(10), 746. https://doi.org/10.3390/photonics9100746



