Theoretical Development of Polymer-Based Integrated Lossy-Mode Resonance Sensor for Photonic Integrated Circuits
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials Fabrication and Characterization
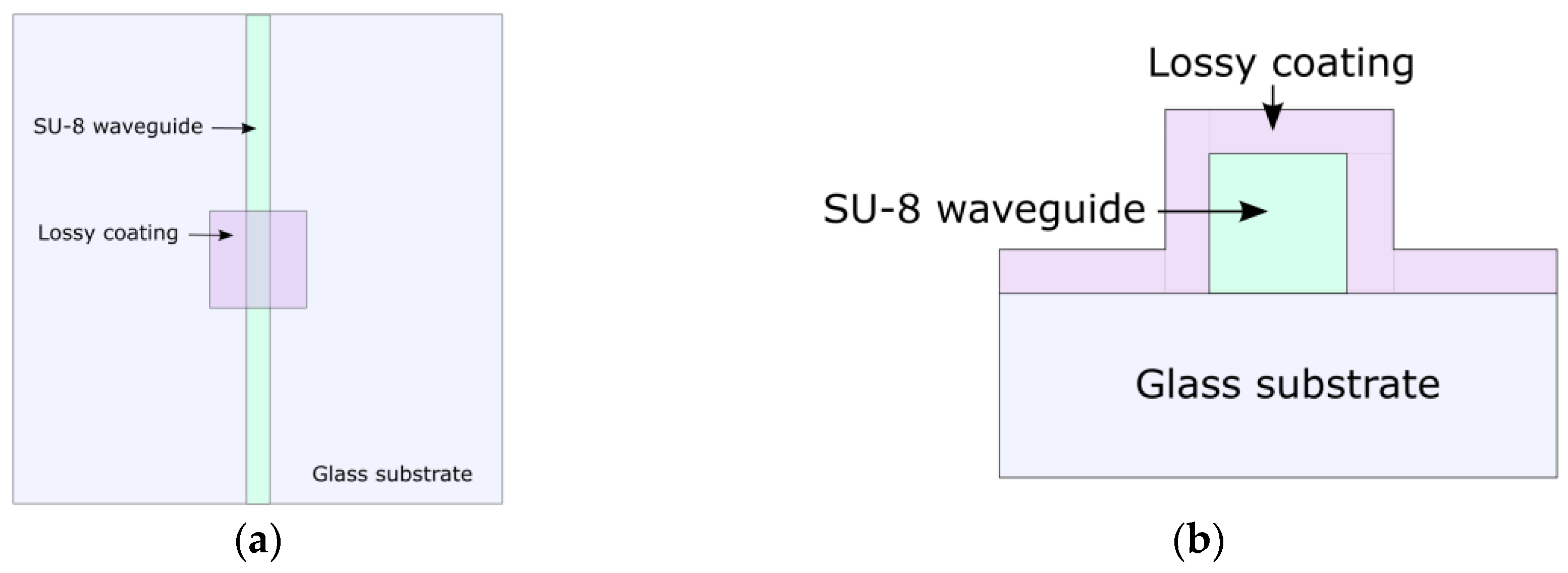
2.2. LMR Device Simulations
2.3. LMR Device Fabrication Guidelines
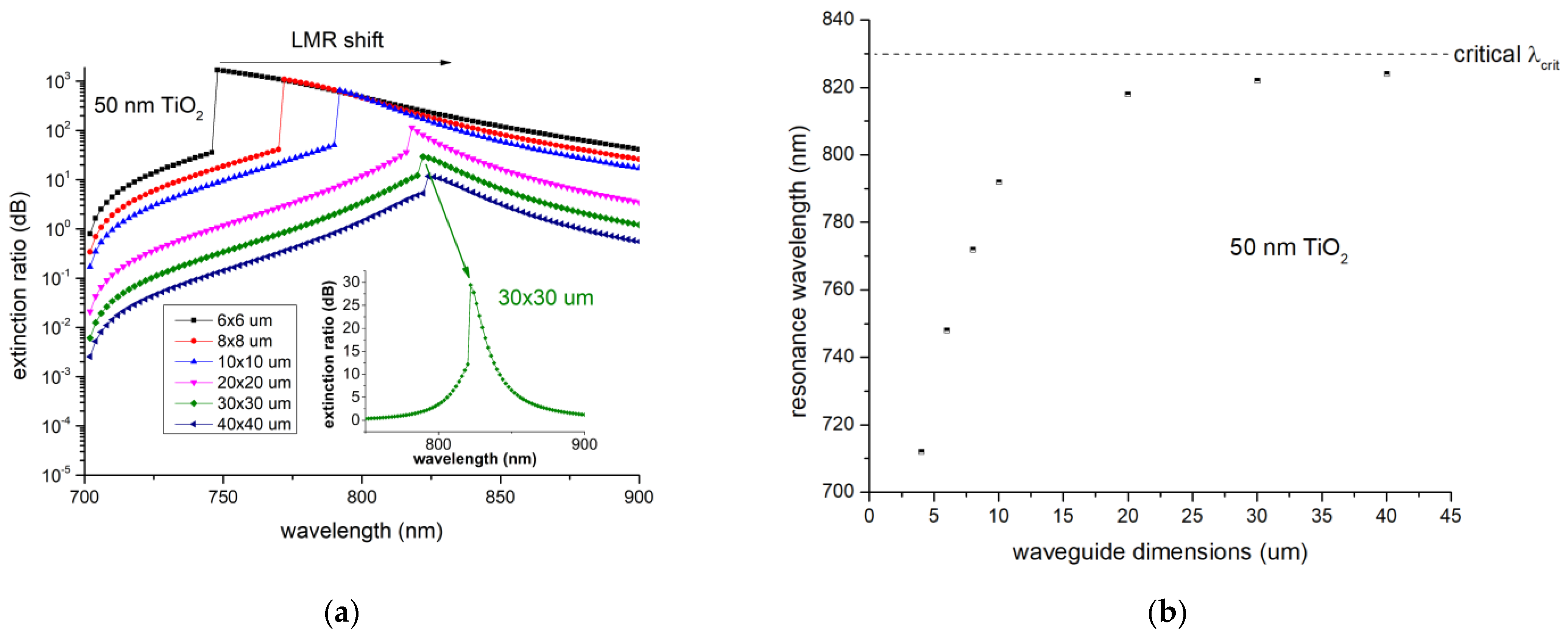
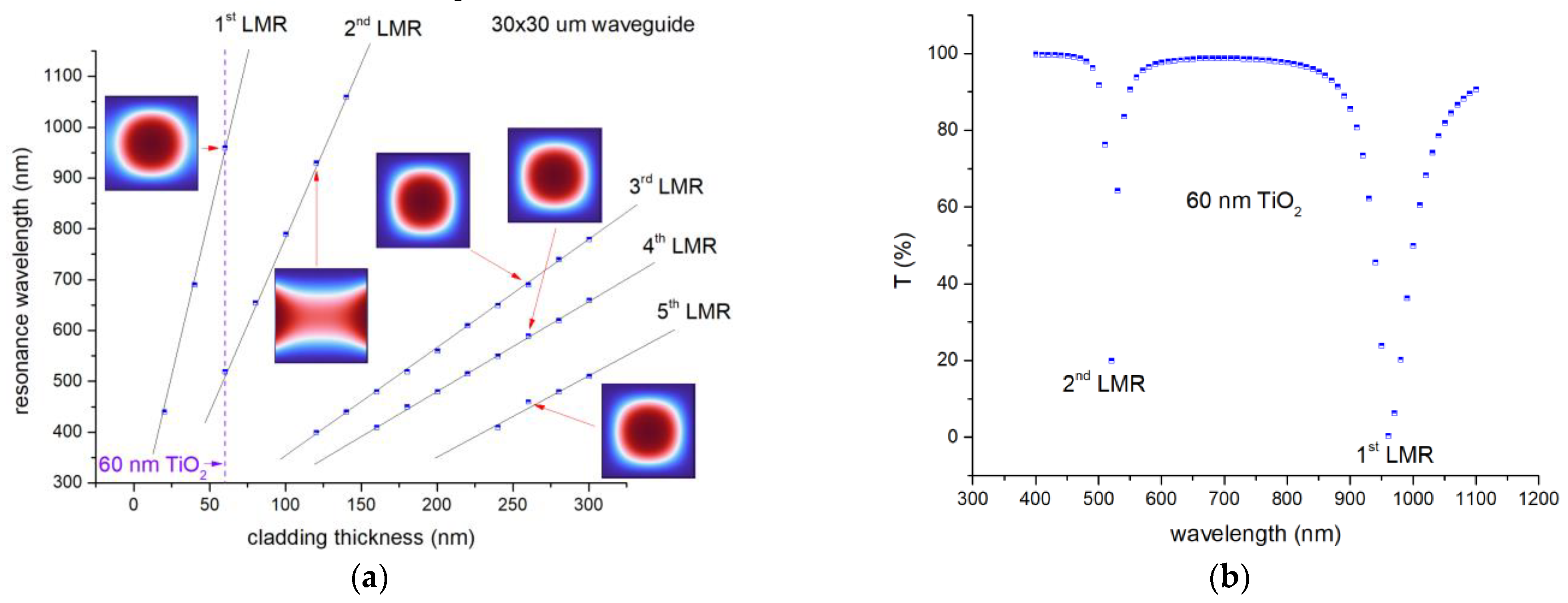
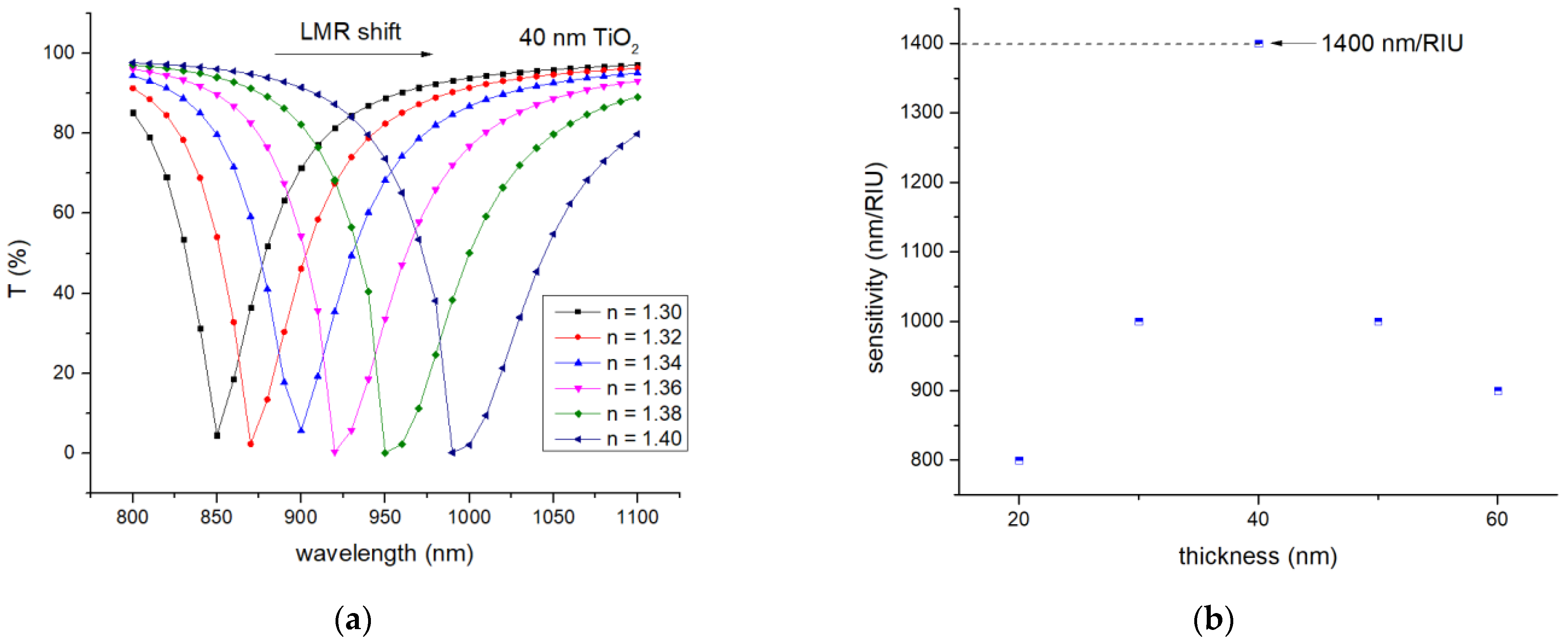
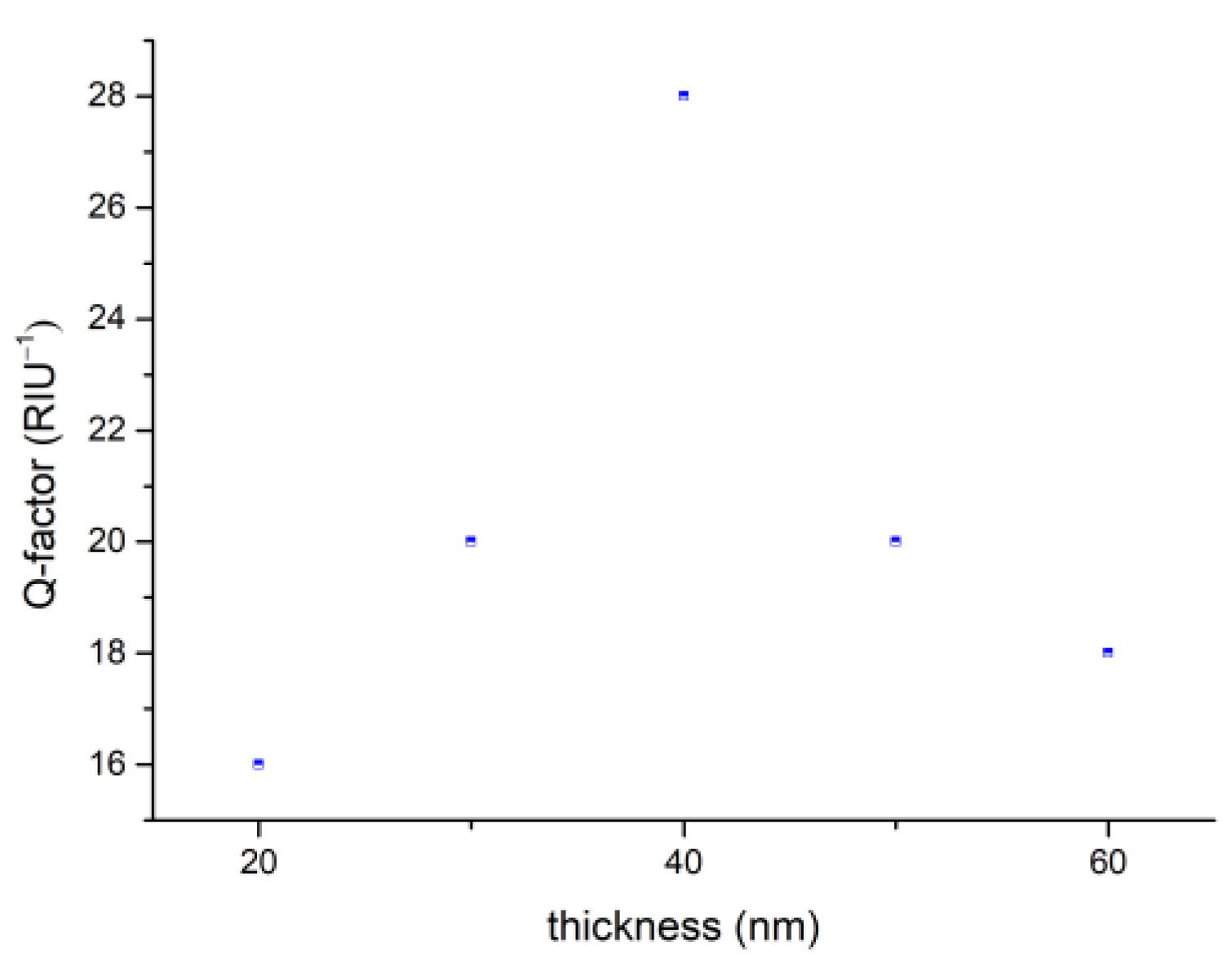
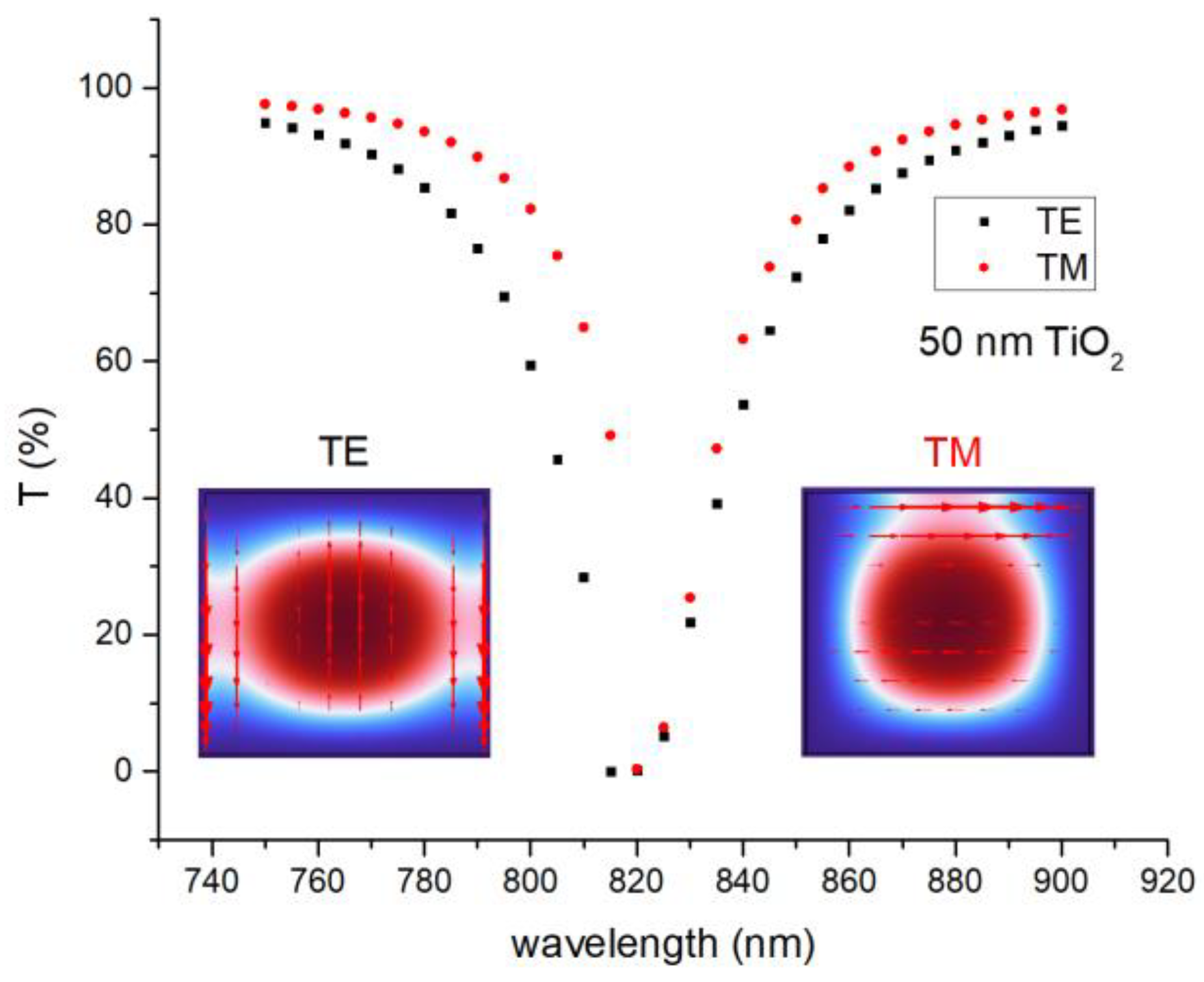
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ali, L.; Mohammed, M.U.; Khan, M.; Yousuf, A.H.B.; Chowdhury, M.H. High-Quality Optical Ring Resonator Based Biosensor for Cancer Detection. IEEE Sens. J. 2019, 20, 1867–1875. [Google Scholar] [CrossRef]
- Inan, H.; Poyraz, M.; Inci, F.; Lifson, M.A.; Baday, M.; Cunningham, B.T.; Demirci, U. Photonic crystals: Emerging biosensors and them Soc irev promise for point-of-care applications. Chem. Soc. Rev. 2016, 46, 366–388. [Google Scholar] [CrossRef] [PubMed]
- Fuentes, O.; Del Villar, I.; Corres, J.M.; Matias, I.R. Lossy Mode Resonance Sensors Based on Lateral Light Incidence in Nanocoated Planar Waveguides. Sci. Rep. 2019, 9, 8882. [Google Scholar] [CrossRef]
- Del Villar, I.; Arregui, F.J.; Zamarreño, C.R.; Corres, J.M.; Bariain, C.; Goicoechea, J.; Elosua, C.; Hernaez, M.; Rivero, P.J.; Socorro, A.B.; et al. Optical Sensors Based on Lossy-Mode Resonances. Sens. Actuators B Chem. 2017, 240, 174–185. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, W.M. A Comprehensive Review of Lossy Mode Resonance-Based Fiber Optic Sensors. Opt. Lasers Eng. 2018, 100, 47–60. [Google Scholar] [CrossRef]
- Zamarreño, C.R.; Hernáez, M.; Del Villar, I.; Matías, I.R.; Arregui, F.J. Optical Fiber PH Sensor Based on Lossy-Mode Resonances by Means of Thin Polymeric Coatings. Sensors Actuators B Chem. 2011, 155, 290–297. [Google Scholar] [CrossRef]
- Zamarreño, C.R.; Hernaez, M.; Del Villar, I.; Matias, I.R.; Arregui, F.J. Tunable Humidity Sensor Based on ITO-Coated Optical Fiber. Sens. Actuators B Chem. 2010, 146, 414–417. [Google Scholar] [CrossRef]
- Fuentes, O.; Goicoechea, J.; Corres, J.M.; Del Villar, I.; Ozcariz, A.; Matias, I.R. Generation of Lossy Mode Resonances with Different Nanocoatings Deposited on Coverslips. Opt. Express 2020, 28, 288. [Google Scholar] [CrossRef]
- Arregui, F.J.; Del Villar, I.; Corres, J.M.; Goicoechea, J.; Carlos, R.; Elosua, C.; Hernaez, M.; Rivero, P.J.; Socorro, A.B.; Sanchez, P.; et al. Fiber-Optic Lossy Mode Resonance Sensors. Procedia Eng. 2014, 87, 3–8. [Google Scholar] [CrossRef]
- Sudas, D.P.; Zakharov, L.Y.; Jitov, V.A.; Golant, K.M. Silicon Oxynitride Thin Film Coating to Lossy Mode Resonance Fiber-Optic Refractometer. Sensors 2022, 22, 3665. [Google Scholar] [CrossRef]
- Eldada, L.; Shacklette, L. Advances in polymer integrated optics. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 54–68. [Google Scholar] [CrossRef]
- Paquet, C.; Kumacheva, E. Nano Structured Polymers for Photonics. Mater. Today 2008, 11, 48–56. [Google Scholar] [CrossRef]
- Lorenz, H.; Despont, M.; Fahrni, N.; LaBianca, N.; Renaud, P.; Vettiger, P. SU-8: A Low-Cost Negative Resist For MEMS. J. Micormech. Microeng. 1997, 7, 121. [Google Scholar] [CrossRef]
- Usha, S.P.; Gupta, B.D. Performance Analysis of Zinc Oxide-Implemented Lossy Mode Resonance-Based Optical Fiber Refractive Index Sensor Utilizing Thin Film/Nanostructure. Appl. Opt. 2017, 56, 5716. [Google Scholar] [CrossRef] [PubMed]
- Nezar, S.; Saoula, N.; Sali, S.; Faiz, M.; Mekki, M.; Laoufi, N.A.; Tabet, N. Properties of TiO 2 Thin Films Deposited by Rf Reactive Magnetron Sputtering on Biased Substrates. Appl. Surf. Sci. 2017, 395, 172–179. [Google Scholar] [CrossRef]
- Chung, H.K.; Won, S.O.; Park, Y.; Kim, J.S.; Park, T.J.; Kim, S.K. Atomic-Layer Deposition of TiO2 Thin Films with a Thermally Stable (CpMe5)Ti(OMe)3 Precursor. Appl. Surf. Sci. 2021, 550, 149381. [Google Scholar] [CrossRef]
- Benítez, M.; Zubiate, P.; Del Villar, I.; Socorro-Leránoz, A.B.; Matías, I.R. Lossy Mode Resonance Based Microfluidic Platform Developed on Planar Waveguide for Biosensing Applications. Biosensors 2022, 12, 403. [Google Scholar] [CrossRef] [PubMed]
- Kadhim, R.A.; Yuan, L.; Xu, H.; Wu, J.; Wang, Z. Highly Sensitive D-Shaped Optical Fiber Surface Plasmon Resonance Refractive Index Sensor Based on Ag-α-Fe2O3 Grating. IEEE Sens. J. 2020, 20, 9816–9824. [Google Scholar] [CrossRef]
- Shahzadi, R.; Shahzad, A.; Qamar, F.; Shahzadi, R.; Ali, M. Effective Refractive Index and V-Parameter Characterization for Guided Modes in Multilmode. Nano and Three Layer Optical Fibers. Int. J. Inf. Technol. Electr. Eng. 2018, 7, 20–27. [Google Scholar]
- Del Villar, I.; Hernaez, M.; Zamarreño, C.R.; Sánchez, P.; Fernández-valdivielso, C.; Arregui, F.J.; Matias, I.R. Design Rules for Lossy Mode Resonance Based Sensors. Appl. Opt. 2012, 51, 4298–4307. [Google Scholar] [CrossRef]
- Tien, C.-L.; Mao, T.-L.; Li, C.-Y. Lossy Mode Resonance Sensors Fabricated by RF Magnetron Sputtering GZO Thin Film and D-Shaped Fibers. Coatings 2020, 10, 29. [Google Scholar] [CrossRef]
- Burnat, D.; Koba, M.; Wachnicki, Ł.; Gierałtowska, S.; Godlewski, M.; Śmietana, M. Refractive Index Sensitivity of Optical Fiber Lossy-Mode Resonance Sensors Based on Atomic Layer Deposited TiO x Thin Overlay. In Proceedings of the Sixth European Workshop on Optical Fibre Sensors (EWOFS’2016), Limerick, Ireland, 30 May 2016; Volume 9916, p. 99161G. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, P.; Zhao, M.; Xu, D.; Wang, J.; Li, Z.; Tang, T.; Shen, J.; Li, C. A High Sensitivity Lossy Mode Resonance Refractive Index Sensor Based on SBS Structure. Results Phys. 2022, 36, 105454. [Google Scholar] [CrossRef]
- Ciminelli, C.; Innone, F.; Brunetti, G.; Conteduca, D.; Dell’Olio, F.; Tatoli, T.; Armenise, M.N. Rigorous model for the design of ultra-high Q-factor resonant cavities. In Proceedings of the 18th International Conference on Transparent Optical Networks 2016, Trento, Italy, 10–14 July 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Madani, A.; Kleinert, M.; Stolarek, D.; Zimmermann, L.; Ma, L.; Schmidt, O.G. Vertical Optical Ring Resonators Fully Integrated with Nanophotonic Waveguides on Silicon-on-Insulator Substrates. Opt. Lett. 2015, 40, 3826. [Google Scholar] [CrossRef] [PubMed]
- Madani, A.; Harazim, S.M.; Quiñones, V.A.B.; Kleinert, M.; Finn, A.; Naz, E.S.G.; Ma, L.; Schmidt, O.G. Optical microtube cavities monolithically integrated on photonic chips for optofluidic sensing. Opt. Lett. 2017, 42, 486–489. [Google Scholar] [CrossRef]
- Saha, N.; Brunetti, G.; Kumar, A.; Armenise, M.N.; Ciminelli, C. Highly Sensitive Refractive Index Sensor Based on Polymer Bragg Grating: A Case Study on Extracellular Vesicles Detection. Biosensors 2022, 12, 415. [Google Scholar] [CrossRef] [PubMed]

| Process Steps | Equipment and Materials Used | Critical Parameters |
|---|---|---|
| Spin coating | Laurell WS650, Gersteltec GM1060 photoresist |
|
| Soft bake | Unitemp high-precision hot plates |
|
| Exposure | Mask aligner Suss MA6 |
|
| Post bake | Unitemp high-precision hot plates |
|
| Development | mr-Dev 600 |
|
| Hard bake | Unitemp high-precision hot plates |
|
| Material | Equation Used | Fitted Parameters |
|---|---|---|
| SU-8 | (1) | |
| SiO2 | (1) | |
| TiO2 | (2) | , . |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Letko, E.; Bundulis, A.; Mozolevskis, G. Theoretical Development of Polymer-Based Integrated Lossy-Mode Resonance Sensor for Photonic Integrated Circuits. Photonics 2022, 9, 764. https://doi.org/10.3390/photonics9100764
Letko E, Bundulis A, Mozolevskis G. Theoretical Development of Polymer-Based Integrated Lossy-Mode Resonance Sensor for Photonic Integrated Circuits. Photonics. 2022; 9(10):764. https://doi.org/10.3390/photonics9100764
Chicago/Turabian StyleLetko, Edvins, Arturs Bundulis, and Gatis Mozolevskis. 2022. "Theoretical Development of Polymer-Based Integrated Lossy-Mode Resonance Sensor for Photonic Integrated Circuits" Photonics 9, no. 10: 764. https://doi.org/10.3390/photonics9100764
APA StyleLetko, E., Bundulis, A., & Mozolevskis, G. (2022). Theoretical Development of Polymer-Based Integrated Lossy-Mode Resonance Sensor for Photonic Integrated Circuits. Photonics, 9(10), 764. https://doi.org/10.3390/photonics9100764





