1. Introduction
With the proliferation of various electronic appliances, the electromagnetic environment has become congested and complex. The operating frequency and bandwidth of communication and radar are becoming higher and larger. This poses great challenges to the comprehensive reconnaissance and receipt of electromagnetic signals in electronic warfare (EW). Consequently, the establishment of receiving systems with low SWaP (Size, Weight and Power) and large dynamic range has attracted tremendous attention. Traditional electronic receivers are limited by the electronic bottleneck of the sampling rate from analog-to-digital (ADC), which makes it difficult to directly receive and digitize wideband electromagnetic signals. Generally, wideband signals can be sampled by low-speed ADCs through serial [
1] and parallel processing [
2]. Alternatively, an electrical sub-Nyquist receiver folds the broadband RF input prior to direct digitization by a narrowband ADC [
3,
4,
5], which enables information recovery with low computational complexity algorithms, based on compressive sensing (CS) principles [
6]. However, the efficiency of the electrical down conversion is unsatisfactory, due to the high timing jitter [
7]. Besides, electronic cables exhibit the deficiencies of high transmission loss and low electromagnetic emission capacity.
The microwave photonic technique has been investigated as a promising option for characterizing and processing wideband RF signals [
8]. It has the dramatic optical merits of wide bandwidth, low loss, immunity to electromagnetic interference, and long-distance transmission [
9]. Contemporary microwave photonic receivers with wide instantaneous bandwidths can be roughly classified into photonic channelization receivers [
10,
11] and sub-Nyquist photonic receivers [
12]. Compared to the channelization system, the Sub-Nyquist photonic receivers employ a single low-speed ADC [
13], which obviates redundant hardware setups, and saves power consumption [
14,
15].
The architecture of sub-Nyquist photonic receivers [
16] originates from the sampled (pulse-based) analog photonic link [
17]. The sampled analog photonic link is applied in wideband radio frequency (RF) signal receivers with carrier frequencies of up to 40 GHz and a bandwidth of 20 MHz [
18]. Nevertheless, the sinusoidal-like transfer response of the electro-optic modulator (EOM) inherently leads to nonlinear distortions [
19,
20]. In addition, the low noise amplifiers (LNAs) for RF signals also induce unexpected nonlinear distortions and inevitable noise. Besides, the harmonic distortions (HD) and intermodulation distortions (IMD) are folded into the first Nyquist zone (NZ) of the sampled analog photonic link. The spurious harmonics of signals with large frequency intervals may produce new aliasing and intermodulation components. In addition, the sampled analog photonic link down-converts the thermal noise and shot noise from all Nyquist zones to the first Nyquist zone. These put immense pressure on the back-end signal processing and seriously deteriorate the working bandwidth, reconnaissance distance, signal-to-noise ratio (SNR), and signal bit error rate (BER). Hence, the intricate spurious distortions and noises of the sampled analog link place restrictions on its practical application in wideband receivers.
There are considerable publications focusing on the linearization of the sampled analog photonic link with nonlinear distortions introduced by EOM. Clark et al. achieved the suppression of third-order intermodulation distortions by 25 dB with an instantaneous bandwidth of 500 MHz [
21]. Urick V. J. et al. applied pre-distortion linearization to improve the spur-free dynamic range (SFDR) of an externally modulated, long-haul analog fiber-optic link by 6 dB in the band range of 6–12 GHz, which may have brought about significant imperfections at the same time [
22]. Besides, R. Duan et al. proposed a digital processing compensation method that realized the suppression of the third-order intermodulation distortion (IMD3) by more than 20 dB [
20]. X. Liang et al. published digital post-compensation methods for a photonic sampling link that realized the suppression of the cross-modulation distortion (XMD) and IMD3 by 33 dB and 25 dB, respectively, which could perform poorly under large dispersion after long-distance transmission [
23]. D. Lam et al. proposed a digital postprocessing linearization technique to efficiently suppress dynamic distortions added to a wideband signal in an analog optical link, which achieved suppression of the IMD by up to 35 dB over multiple octaves of signal bandwidth [
24]. Y. Dai et al. proposed a digital linearization by directly acquiring the output third-order intercept point from the system hardware, which improved the SFDR by using a high-performance pre- and post-amplifier [
25].
These linearization schemes generally required construction of a well-designed distortion-matched hardware path with careful synchronization between the distortion and compensation signals [
26], or the addition of further optical devices [
27]. Moreover, most of them could only eliminate the nonlinearities caused by the EOM. The nonlinear distortions caused by other devices (like amplifiers), and the noise interferences are rarely coped with simultaneously. Therefore, it is still a great challenge to automatically suppress the nonlinearity and noise of various sources in sub-Nyquist photonic receivers for wideband signals.
In recent years, deep learning (DL) has made remarkable achievements in image denoising [
28,
29], speech enhancement [
30,
31], optical image reconstruction [
32,
33] and other related fields [
34,
35]. Applying deep neural networks to photonics processing that are difficult to realize by traditional processing algorithms exhibits tremendous attractive perspectives. Deep neural networks can automatically extract the characteristics of signals and analyze the extracted features by establishing the mapping relationship between inputs and outputs in a regression task. By training the models in a way of approaching the minimum value of the loss function with adequate datasets, the deep neural models could adaptively convert the untrained input to the expected target output and dispense with the complicated mathematical operation.
Recent developments in applying deep learning to photonic links have attracted much attention. Wan et al. proposed an artificial neural network (ANN) equalizer to mainly mitigate the nonlinear impairments of optical fibers [
36]. Zhou et al. proposed a microwave photonic instantaneous frequency measurement scanning receiver, in which deep neural network frequency estimation was used to deal with system defects and improve accuracy [
37]. Xu et al. proposed two deep neural networks to recover the nonlinear effect and channel mismatch for a two-channel photonic ADC, which improved the effective number of bits (ENOB) of the single-tone signals with an input frequency of 23.332 GHz [
38]. Furthermore, they applied the modified photonic ADC in real scenarios with complicated signals utilizing the same setup, which improved the SFDR by ~18 dB [
39]. Subsequently, Yi et al. proposed a transfer-learning network in a 20 GS/s photonic system for denoising multiband signals [
40]. Besides, Zou et al. investigated a simplified convolutional recurrent autoencoder (CRAE) network for the mismatch compensation of a channel-interleaved photonic analog-to-digital converter (PADC), which improved both the frame rate and the dynamic range [
41].
In this paper, we applied a deep residual network (Resnet) in a sub-Nyquist photonic receiver to realize the adaptive linearization and lower the noise floor at the same time. Compared to the conventional linearization methods, the deep learning method requires no complicated hardware setups or miscellaneous digital processing steps, and it is suitable for dealing with multi-source nonlinear spurious distortions. To our knowledge, this is the first attempt that realizes adaptive linearization for a sub-Nyquist photonic receiver with RF signals ranging up to 40 GHz, which are available to single-tone signals, multi-carrier signals, wireless communication signals, and linear frequency modulation (LFM) signals. More importantly, due to the characteristics of adaptive intelligence, the deep learning method is more suitable for non-cooperative communication scenarios and applicable to the time-varying electromagnetic environment.
2. Materials and Methods
A proof-of-concept experimental setup based on the sub-Nyquist photonic receiving system is illustrated in
Figure 1. The optical source was a self-developed mode-locked fiber (MLL) laser, based on a semiconductor saturable absorption mirror with long-term stability. The optical pulse width was 247 fs and the spectral width was 10.10 nm. The MLL was amplified by an erbium-doped fiber amplifier (EDFA) (Accelink, EDFA array series, Wuhan, China) with an output power of 20 dBm. The RF signals modulated the MLL through a Mach–Zehnder intensity modulator (MZM) (iXblue, MXLN-40, Paris, France), and the frequency modulation range of the RF signal was up to 40 GHz. Subsequently, the photoelectric conversion process was carried out by an encapsulated high-speed positive –intrinsic–negative (PIN) photodetector (PD) (Bonphot Optoelectronics, PD03, Suzhou, China). The output down-converted RF signals were amplified by a tailor-made wideband low-noise amplifier (YQAMP01040, LNA), and then the high-frequency components were filtered out by a low-pass filter (LPF). The receiving signals were sampled and observed by a 20 GS/s Oscilloscope (Rohde & Schwarz, RTO2044, Muenchen, Germany). After the analog-to-digital process, the digital signals were processed by digital signal processing (DSP), and then fed into the deep learning (DL) module, where the signals polluted by multi-source distortions could be automatically linearized.
The down-conversion principle of receiving signals with deep learning-assisted linearization is shown in
Figure 1 as well. In the frequency domain, the mode-locked laser was performed as an optical frequency comb (OFCs) with a repetition rate of ~1030 MHz. The Nyquist zone was expressed from 1 to N with a frequency width of 515 MHz. To maximize the down-conversion efficiency, the RF signals were copied to every optical frequency comb through the MZM with dual-sideband modulation mode. After the propagation through optical fibers, the loaded RF signals beat with the near combs in the photoelectric conversion process. The copies of down-converted RF signals, harmonic distortions, and intermodulation distortions emerged via direct detection through PD. Subsequently, the high-frequency components were filtered by the low-pass filter, and all the frequency components falling into the first Nyquist zone could be sampled by a low-speed ADC. Ultimately, the harmonics and intermodulation distortions were suppressed by the deep learning method.
As deep learning is a data-driven approach, the appropriate dataset generation provided for training and testing is essential. The datasets were derived from the down-converted duplicates of single-tone sinusoidal signals, dual-tone sinusoidal signals, wireless communication signals, and linear frequency modulation (LFM) radar signals. The single-tone and dual-tone sinusoidal signals were generated by a microwave analog signal generator (Sinolink Technologies, SLFS-440D, Beijing, China) with various frequencies (0–40 GHz) and amplitudes (0 dbm–20 dbm). The wireless communication signals were generated and transmitted from a universal software radio peripheral (USRP) (National Instruments, USRP-2794, Austin, TX, USA) with multiple modulation formats and carrier frequencies (0–6 GHz). The LFM signals were generated by an Arbitrary Waveform Generator (Tektronix, AWG5202, Tokyo, Japan).
To produce the training targets (reference data) for the deep neural network, the acquired receiving raw digital signals were preprocessed using digital signal processing (DSP) filtering algorithms in the time domain. Afterward, every processed reference signal and the raw signal were dominated as a pair of reference/raw data. All the reference/raw data pairs constructed the total datasets. As shown in
Figure 2, the deep learning module was divided into two processes: training and testing. Correspondingly, the datasets were randomly split into training datasets and testing datasets, with a ratio of 0.2 without overlap (169 samples for training and 47 samples for testing). In brief, the testing datasets were set as validation datasets to monitor the fitting states of the network. The deep learning layers and training process were implemented by the Keras framework from TensorFlow on the Nvidia TITAN RTX GPU.
In this work, we designated a deep residual network (Resnet) that was inspired by the field of computer vision (CV). It is supposed that a deeper network can extract more complex feature patterns by increasing the number of network layers. However, this may raise problems of gradient disappearance or gradient explosion, which make the deep learning model difficult to train. The Resnet solves the gradient degradation problem of the deep network through residual learning, so as to realize the training of a deeper network [
42]. From a mathematical point of view, the residual unit can be expressed as:
Among the Equations (1) and (2),
and
represent the input and output of the
residual unit, respectively. The residual function is represented by
, which represents the learned residual. The identity mapping is represented by
, and
is the activation function. Based on the above formulas, the learned characteristics of the units from
to
are as follows:
Using the chain rule, the reverse gradient can be obtained by Equation (4). The first factor () of the gradient in Equation (4) represents the gradient of the loss function reaching . The residual mechanism can propagate the gradient lossless, while another residual gradient needs to pass through the layer with weights, and the gradient is not transmitted directly.
Figure 2 presents the schematic diagram of the designated deep Resnet, which was constructed with 20 residual blocks. Every residual block was formed with two cascaded 1D convolutional layers, and each 1D convolutional layer was constituted by 32 filters. The kernel size of each 1D convolutional layer was set to 16. In the residual learning schemes, the output of every block was summed with the input data. To ensure the same scale of input and output, the final 1D convolutional layer with 1 filter was added. Specifically, since the signals have both positive and negative amplitude values, to avoid the gradient disappearance, the leaky rectified linear units (
) function was employed as the activation layer at the end of every 1D convolutional layer. The loss function of the
is depicted in Equation (5), where
is a constant.
During the training process, we conducted the supervised learning scheme of the deep neural network by minimizing the Mean Absolute Error (
) loss function between the rectified data (output) and raw data (input). The loss function is shown in Equation (6). In detail, as shown in
Figure 2, the input of the deep Resnet was the raw time-domain signal waveform, and the training target was the reference time-domain signal waveform. In the testing process, the untrained raw data was fed into the trained model, while the output of the model was the linearized time-domain signal waveform data.
The hyperparameter settings are shown in
Table 1. The length of the input signal data was intercepted to 49,900 before being fed into the Resnet. Furthermore, Adam was adopted as the optimizer, and the initial learning rate was set to 0.001. To ensure adequate learning capacity, the initial quantities of epochs were set to 10,000. Meanwhile, the early stopping mechanism was introduced to prevent overfitting, in which the training was stopped when the loss function did not change after 150 epochs. In addition, we applied the adaptive learning rate reduction mechanism (ReduceLROnPlateau), in which the learning rate was reduced by 1% when the loss function of the validation set was no longer reduced after 50 epochs.
3. Results and Discussion
To ensure reasonable learning capacity during the training process, the loss functions of the training dataset and validation dataset were monitored.
Figure 3a depicts the training and validation loss curves of the Resnet model. The training loss and validation loss were calculated by the absolute error between the network output and the reference data on the training set and validation set, respectively. Essentially, due to the early stopping scheme, which remedied the overfitting and saved the training time, the training process experienced 5535 epochs. The training loss was reduced from 14.450 to 0.0560, while the validation loss was stable at 0.0604. The training loss showed the same convergence trend as the validation loss. Furthermore,
Figure 3a also elucidates the curve of the learning rate, in which the optimal model was obtained when the learning rate was reduced to 10
−6. From the convergence of the two loss functions of the Resnet model, the learning mode was explicitly correct where there was no abnormal state of overfitting or underfitting.
Figure 3b,c depicts the distribution of the samples on the training set and testing set in different loss values, respectively. This ensured that the sample distribution of the training set and testing set was basically the same, and most samples were concentrated between 0.005–0.020. The training process took about 71,244.4 s.
In the sampled analog photonic link, all the high-frequency components were supposed to be down-converted within the first Nyquist zone (0–515 MHz). Hence, it was sufficient to set the frequency observation window, which just accommodated the first Nyquist zone. According to the down-conversion principle of the sampled analog photonic link, the mapping relationship of the input frequency to the output frequency is described by Equation (7), where
is the comb of the optical frequency comb, which is the nearest comb to the signal, and
is the repetition frequency of the OFC.
Figure 4 displays the effects of the deep learning-assisted spurious elimination spectrum of the single-tone sinusoidal signals formed by splicing the spectrums of several representative frequency bands from 0–40 GHz. All the input frequency components were down-converted to the first Nyquist zone (0–515 MHz) after being received by the sub-Nyquist photonic link. It should be noted that when the power of the input signal is high, the harmonic and intermodulation distortions will also fall into the first Nyquist zone. As shown in
Figure 4, with the aid of deep learning linearization, intricate distortions like the down-converted second-order harmonics and third-order harmonics were automatically suppressed under the condition of unknown signal frequency information. Significantly, the deep learning method also reduced the noise floor (NF) to improve the
in all covered frequency bands.
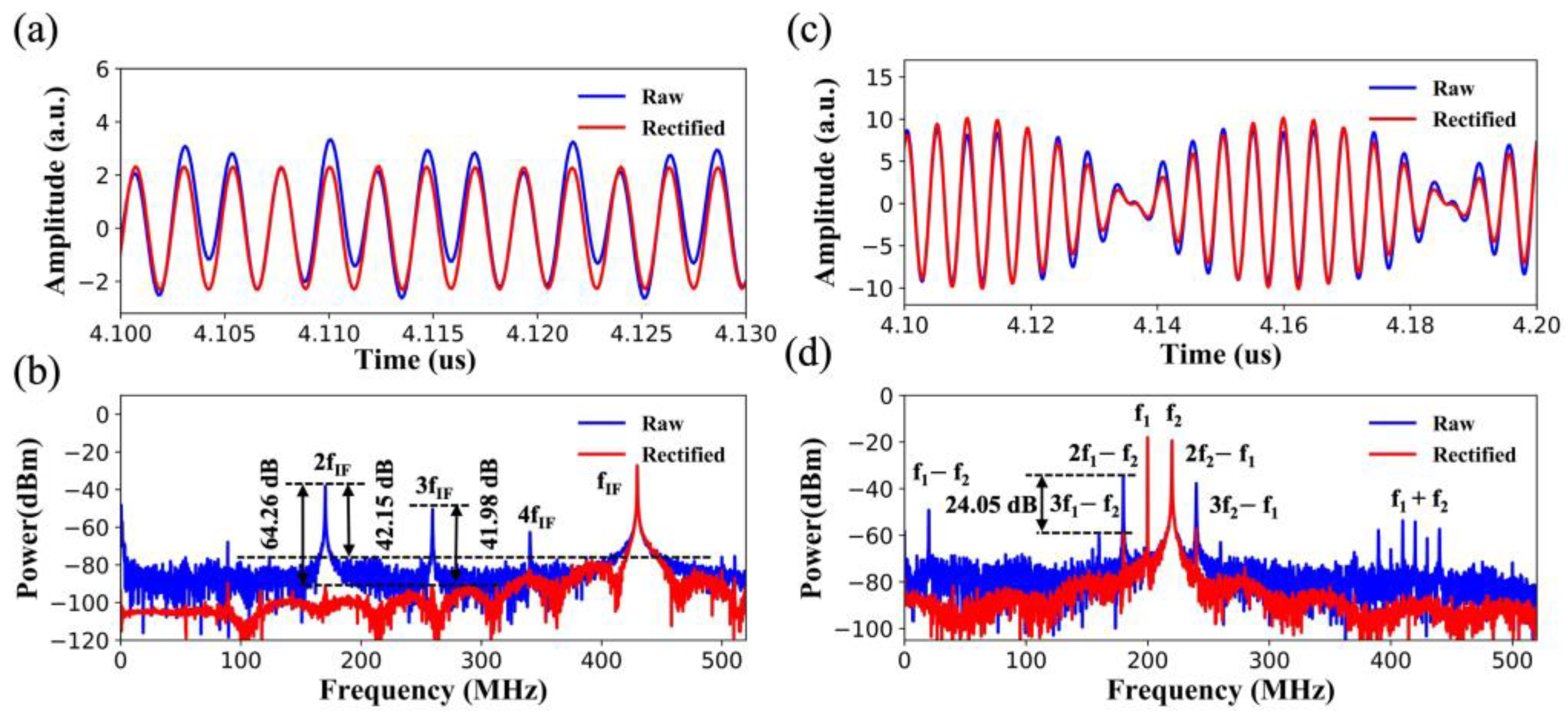
Figure 5a,b show the intuitive effects of eliminating spurs of a single-tone sinusoidal signal in the perspectives of the time domain and frequency domain. The frequency of the input signal was 0.60 GHz and was folded to 430 MHz by the sub-Nyquist photonic link. Simultaneously, the down-converted second harmonic (170 MHz), third harmonic (260 MHz), and fourth harmonic (340 MHz) occurred due to the nonlinearity of the MZM and LNA. As shown in
Figure 5a, the signal rectified by the Resnet model was more inclined to a standard sinusoidal signal, as a result of dispelling the intricate spurious distortions and noise floor of the raw signal data.
As depicted in Equation (8), the spurious suppression ratio
of the sampled analog photonic link can be equivalently defined as the ratio of the power of the signal to the power of the largest harmonic or distortion, which can be calculated from the spectra. The
could be calculated as the power of the signal to the power of the noise, as depicted in Equation (9). From the perspective of the frequency domain in
Figure 5b, the
improved by about 42.15 dB, owing to the deep learning method. Specifically, the second harmonic was suppressed by about 64.26 dB, and the third harmonic was suppressed by about 41.98 dB. Simultaneously, the noise floor in the first NZ declined from about −80 dBm to −95 dBm on average.
In addition, the intermodulation distortions in multi-carrier scenarios can be effectively suppressed by using the proposed deep learning method. In the proof-of-concept experiments, the input multi-carrier RF signals were emulated by dual-tone sinusoidal signals at frequencies of 200 MHz and 220 MHz, as shown in
Figure 5c,d. The input powers of the dual-tone signals were 16 dBm. Correspondingly, the third-order intermodulation distortions (IMD3) were located at 180 MHz and 240 MHz, respectively.
Figure 5c shows a comparison of the measured waveform of the raw dual-tone signals with sophisticated spurs and the rectified waveform after the deep learning linearization.
Figure 5d depicts the spurious suppression effects of the deep learning method in the frequency domain. The
of the first Nyquist zone was optimized from 16.93 dB to 40.98 dB, and increased by 24.05 dB. The IMD3 with a frequency of 180 MHz was suppressed from −35.06 dBm to −59.20 dBm. Interestingly, for the second harmonics (400 MHz and 440 MHz), the products of the frequency separation of the two signals (20 MHz), and the fifth-order intermodulation distortions (IMD5,160 MHz and 260 MHz) were suppressed.
Figure 6a displays the measured powers of the folded third-order intermodulation distortion (IMD3), the fifth-order intermodulation distortion (IMD5), and the sum-frequency sidebands as a function of the input RF powers, with and without deep learning-assisted signal linearization. Owing to the deep learning method, the suppression of the IMD3 could be realized up to 28.9 dB, and the suppression of the IMD5 could be realized up to 21.3 dB. Meanwhile, the suppression of the sum frequency (420 MHz) could be realized up to 44.1 dB. It was demonstrated that the Resnet could automatically recognize the dual-tone signals and suppress the stray components, except for signals at one time without any prior knowledge.
The third-order-spurious-free dynamic range (
) is generally an essential evaluation criterion of the photonic link, which can be calculated in the format distributed in Equation (10). The
is the output cut-off point of the third-order nonlinear distortion component, and
N0 is the output noise of the link normalized in 1 Hz.
By varying the input RF powers, both the powers of the target intermediate frequency (IF) and IMD3 sidebands were monitored and dominated the major powers.
Figure 6b depicts the comparison of the
with and without the deep learning method. The slope for the third-order-inter-modulation component was 3. The measured raw noise floor was −133 dBm/Hz, which was reduced to −148 dBm/Hz after the deep learning processing. The
was improved from 96.92
to 115.08
, which indicated that the
enhancement was 18.16
. It should be noted that the current
was also restricted by the quantization noise of the electrical ADC, which cost a lot in hardware upgrade.
Figure 7a,b show the effects of signal linearization testing on wireless communication quadrature phase-shift keying (QPSK) signals. The carrier frequency of the testing example of the QPSK signal was 0.14 GHz. It was confirmed that the deep Resnet model delineated the compelling generalizing capacity on wideband wireless communication signals. In detail, it is observed that the burr noises were eliminated in the time domain waveforms in
Figure 7a. In
Figure 7b, the
was improved from 25.67 dB to 65.46 dB on wideband communication QPSK signals, realizing an improvement of 39.86 dB. Specifically, the second harmonics (280 MHz) and third harmonics (420 MHz) were almost eliminated. The noise floor dropped by about 15 dB, which improved the
without any loss of the intensity of the signals.
Besides, LFM radar signals with wide bandwidth were also exploited to validate the proposed model. The testing LFM signal was centered at 50 MHz with a bandwidth of 80 MHz. As with the other kinds of signals, it is observed that the burr noises were eliminated in the time domain waveforms in
Figure 7c. In
Figure 7d, the
was improved by about 25.39 dB. At the same time, the noise floor dropped by about 15 dB.
4. Conclusions
In conclusion, it is inevitable that inherent hardware imperfections cause the transmitted signal to deviate from its ideal representation in sampled analog photonic links. Particularly, the HD and IMD distortions introduced by MZMs and LNAs severely deteriorate the quality of the received signals. To solve these problems, a deep Resnet was designated to adaptively mitigate the multifactorial spurious distortions and noises, while simultaneously maintaining the rare patterns of signals.
The experimental results validated that the deep learning linearization method could automatically suppress spurious distortions with frequencies of 0–40 GHz. It was available for different types of signal generators and signal modulation types, including single-tone signals, dual-tone signals, wireless modulated communication signals, and LFM wideband signals. The proposed method could improve the and by 42.15 dB and ~15 dB, respectively.
In contrast to the previous linearization methods, the deep learning method could synchronously handle the multi-source induced spurious distortions and noise interference that are intractable for traditional digital signal processing techniques. Meanwhile, it could save miscellaneous hardware resources, and is expected to lower the SWaP of the receiver. The capabilities shown in the high-frequency and multi-carrier signals processing are also promising for ultra-wideband (UWB) microwave signal processing.
In the future, the proposed deep learning algorithms could be ported to embedded applications, such as field-programmable gate arrays (FPGA), for real-time signal processing. Besides, we could explore the possibility of applying the deep learning linearization method to other photonic links as well.