Ultra-Wideband Polarization Insensitive Angle Filter Based on ENZ Characteristics and Dynamic Antireflection Structures

Abstract

Bandwidth expansion has always been an important dimension in investigating angle filters (AFs) and is critical for optical communication and radar detection. In this paper, the AF with strong selectivity is realized by using the epsilon-near-zero (ENZ) jump characteristic of YaBa₂Cu₃O₇ material. At the same time, for both the TE and the TM waves in the range of 237~1000 THz, the transmissivity of the AF is stronger than 0.9 by using dynamic antireflection structures (AFSs). The transfer matrix method is suitable for theoretical calculation, and the impedance matching theory is introduced to analyze the features of the AF. The increment of the thickness of superconductor material can effectively enhance the selectivity of the AF structure, and the consequence is the attenuation of transmission performances. If the temperature is covered from 0 K to 85 K, the filtering performance higher than 0.9 can still be maintained for two polarization waves. For these explicit performances, the proposed design may provide a new idea for widening the frequency bandwidth of the AF.

1. Introduction

Frequency, propagation direction, and polarization are three basic properties of the monochromatic plane wave. Among them, studies on frequency and polarization are quite common, and the technologies are relatively mature, while the exploration of angle selectivity has been a huge challenge [1,2,3]. Compared with the other two dimensions, scientific development is quite slow. In fact, highly selective propagation direction plays an irreplaceable role [4,5,6] in optical communication, solar energy absorption, radar detection, imaging systems, and other fields, so it is of indelible significance to overcome the challenges in the angle domain. Many efforts have been made to promote the development of angle filters (AFs), including the diffraction effect of photonic crystals [7,8,9], gratings [10,11], Brewster angle [12,13,14,15], Fabry Perot resonance [16,17,18,19,20], and so on. However, they can only support narrowband selectivity or are limited by the polarization mode, which greatly limits the practical application of AFs.

In 2014 [14], Shen et al. designed a wide-band AF for the TM wave by using the Brewster angle mode, while for the TE wave, there exists no angle selection function. The medium with a permeability not equal to 1 is adopted, which is difficult to realize in practical application. At the same time, the author arranges the structures in the way of a function stack, which brings great trouble to the process of manufacturing. Although there are several optimization works in this paper, the idea of realizing AFs based on the layered structure points out the direction that can be followed by future generations, which has a guiding role in the development of AFs. In 2016, Iizuka et al. [21] proposed a polarization-independent AF structure in theory by using the diffraction effect of photonic crystals and verified the reliability of the theory through experiments two years later, and the angle window has a strong selectivity with a high rectangular coefficient. Unfortunately, due to the resonant characteristics of photonic crystals, the frequency bandwidth is wispy, and theoretically, the application of AFs should have a wide bandwidth. In 2018, Qu et al. [22] constructed a system composed of anisotropic photonic crystal stacks and half-wave plate materials based on the structure used by Shen et al. to achieve a polarization-independent broadband AF structure. However, the rectangular coefficient of this structure is slightly inferior. In 2021, Wan et al. [8] put forward a nonreciprocal and polarization separation angle selection based on asymmetric arrangement mode. On the premise of maintaining high absorption and a strong rectangular coefficient, a quasi-periodic method was used to broaden the frequency bandwidth, but it is still a narrow band category. It can be seen that predecessors have made many attempts to break through the broadband high-performance AF structures that do not depend on polarization, but there is still great room for improvement.

In this paper, by virtue of the low loss and ENZ characteristics of YaBa₂Cu₃O₇ superconducting materials [23], AF properties with productive selectivity are used, and the angular selectivity can be conspicuously improved by the extension of the thickness of YaBa₂Cu₃O₇. For the sake of optimizing transmission performance, dynamic antireflection structures (AFSs) are added on both sides of the host YaBa₂Cu₃O₇ layer, which are composed of YaBa₂Cu₃O₇ and air layers. This makes the impedance of the host structure and the AFSs drift at the same time when the external conditions convert to achieve the effect of dynamic balance. Compared with the fixed refractive index of the medium with the AFSs, the dynamic AFSs greatly highlight the advantages of frequency bandwidth. The proposed design concept avoids the influence of polarization waves, and the transmissivity is higher than 0.9 in the super bandwidth of 237~1000 THz. The rise of temperature can regulate the filtering angle, and the filtering performance is always superior in this process.

2. Materials and Methods

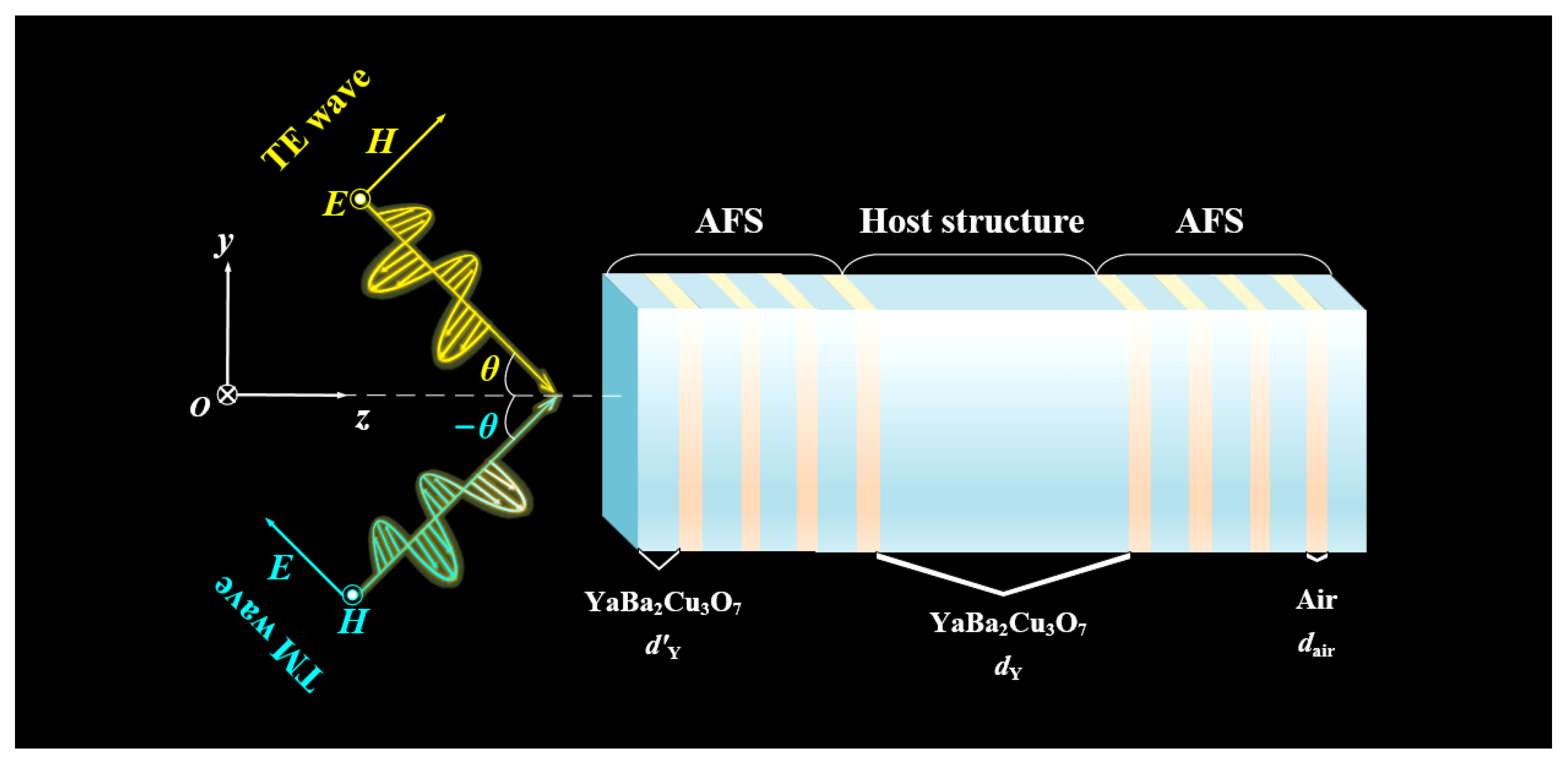
In Figure 1, the propagation direction of wave vector k is in the yoz plane, the electric field direction of the TE wave is perpendicular to the plane of the propagation direction, the incidence angle is θ, the magnetic field direction of the TM wave is perpendicular to the propagation plane, and the incidence angle is expressed by −θ. The design model consists of the host structure and 2 AFSs. The host structure has the potential to produce highly selective angle filtering, while AFSs are used to suppress reflection and enhance impedance matching. The dynamic AFS means that when the frequency shifts, the impedance of the host structure and that of the AFS alter simultaneously to achieve dynamic impedance matching in a wide frequency range, broadening the frequency band. The refractive index of the air layer is n_air = 1, and the thickness is d_air = 35 nm. For YaBa₂Cu₃O₇ materials, $n_{\mathrm{Y}}=\sqrt{{\epsilon }_{\mathrm{Y}}}$, the dielectric function is described by the 2-fluid model and London local electrodynamics. When the temperature is lower than the critical temperature, the superconductor can be regarded as lossless, and the dielectric function model can be described as [24,25]:

$${\epsilon }_{\mathrm{Y}}=1-\frac{1}{{\omega }^2{\mu }_0{\epsilon }_0{\lambda }_L^2}$$

(1)

where, λ_L is the temperature-dependent London penetration length, which is given by,

$${\lambda }_L=\frac{{\lambda }_L(o)}{\sqrt{1-{\left(\frac{T}{T_C}\right)}^P}}$$

(2)

λ_L(o) is the London penetration length at T = 0 K, P = 4, and T_C = 92, K is the superconducting critical temperature.

Figure 1. The above is the proposed AF model diagram. The host structure is a single-layer superconducting YaBa₂Cu₃O₇ material, and the dynamic AFSs on both sides are composed of YaBa₂Cu₃O₇ materials and air layers alternately.

Figure 1. The above is the proposed AF model diagram. The host structure is a single-layer superconducting YaBa₂Cu₃O₇ material, and the dynamic AFSs on both sides are composed of YaBa₂Cu₃O₇ materials and air layers alternately.

In the case of an ultra-low temperature, the effect of thermal expansion is also considered, which is depicted in the thickness of superconducting materials [23].

$$d^{*}=d+\alpha d\Delta T$$

(3)

In which, d is the thickness of the layer at room temperature and d* is the thickness at ultra-low temperatures, α is the thermal expansion coefficient of the medium. The initial temperature is set as T = 55 K, and ΔT refers to the difference from room temperature.

In the AFSs, the thickness of the superconductor layer is d’_Y = 60 nm, and in the host structure it is d_Y = 2000 nm.

The energy transfer between dielectric layers can be calculated by the transfer matrix method [21,23].

$$M=\left[\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}\right]={(M_{Y^{\prime }}{M}_{air})}^4{M}_Y{(M_{air}{M}_{Y^{\prime }})}^4$$

(4)

For each layer of dielectric, the transfer matrix can be described as:

$$M_i=\left[\begin{array}{cc}\cos {\delta }_i& -j{p_i}^{-1}\sin {\delta }_i\\ -j{p}_i\sin {\delta }_i& \cos {\delta }_i\end{array}\right]$$

(5)

Among them, $p_i=\sqrt{{\epsilon }_0/{\mu }_0}{n}_i{d^{*}}_i\cos {\theta }_i$, ${\delta }_i=(2\pi /\lambda )n_i{d^{*}}_i\cos {\theta }_i$.

The reflection coefficient r and transmission coefficient t can be expressed by the following formulas:

$$r=\left|\frac{\left(M_{11}+M_{12}{p}_0\right)p_0-\left(M_{21}+M_{22}{p}_0\right)}{\left(M_{11}+M_{12}{p}_0\right)p_0+\left(M_{21}+M_{22}{p}_0\right)}\right|$$

(6)

$$t=\left|\frac{2p_0}{\left(M_{11}+M_{12}{p}_0\right)p_0+\left(M_{21}+M_{22}{p}_0\right)}\right|$$

(7)

The reflectivity R and transmissivity T can be described as:

$$\begin{array}{l}R=r^2\\ T=t^2\end{array}$$

(8)

3. Results

According to the dielectric function calculation formula of YaBa₂Cu₃O₇ materials, with the increase in frequency, ε_Y gradually rises, changing from a negative to a positive value, and there is an intersection point with zero value at the frequency of 223 THz, as the blue discrete ball shows in Figure 2. In order to succinctly reflect the energy propagation process, the incidence angle is selected as zero degrees, resulting in no difference in transmission characteristics between the TE and TM waves. At the same time, near the ENZ critical point, the transmission characteristics of the electromagnetic wave suddenly change from the strong reflection state to the high transmission state, and the transmissivity is higher than 0.9, as shown in the curve of the red ball in the figure. It can be imagined that when the real part of ε_Y is less than zero, it means that the real part of the medium is zero, and there is a large loss. The strong ion action in the medium causes strong interference with electromagnetic waves, and it is difficult for the energy to penetrate the superconductor. However, when ε_Y is greater than zero, superconductors show lossless characteristics, which are equivalent to transparent for electromagnetic waves.

Inspired by Figure 2, at the ENZ critical point, the transmissivity in the frequency domain will jump. Similarly, if the investigation is transferred to the angle domain, transience will also occur. Considering the regulation of angle areas on the transmission spectrum, f = 500 THz is picked up for further exploration. In Figure 3a, when only the host structure is working without AFSs, the TM wave will have a conversion of transmission characteristics at −61.9 degrees, while the TE wave will have a similar phenomenon at 61.9 degrees. However, due to the resonance factors of the medium itself, the energy is leaked near the critical angle, forcing the transmissivity to be far lower than 0.9, which is not conducive to the normal operation of the device. Consequently, an appropriate AFS is necessary. On both sides of the host structure, AFSs are arranged alternately by YaBa₂Cu₃O₇ materials and air layers. Remarkably, the electromagnetic wave leakage is suppressed, and the transmissivity under both polarization waves is higher than 0.9. For the sake of exploring the mechanism of the AF more distinctly, the impedance matching theory is utilized to analyze the structure. The normalized surface impedance is defined as the ratio of the impedance of the entire structure to the impedance of the vacuum wave [8]:

$$\frac{Z_{eff}}{Z_0}=z_{r,eff}+j{z}_{i,eff}=\frac{1+r}{1-r}$$

(9)

In which, Z₀ = |E₀|/|H₀| = (μ₀/ε₀)^1/2 is the vacuum wave impedance, whose value is about 377 Ω. Z_eff = |E|/|H| = (μ/ε)^1/2 is the effective impedance of the entire structure. r infers the reflection coefficient. After analysis, when the real parts and imaginary parts of normalized surface impedance are close to one and zero, respectively, the impedance matching degree is best and reflection can be suppressed to the greatest extent. The curve distribution in Figure 3b also meets this feature.

Figure 3. (a) Description of the influences of the presence and absence of AFSs on filtering performance; (b) distribution of the real and imaginary parts of the surface effective impedance in the presence of AFSs.

Figure 3. (a) Description of the influences of the presence and absence of AFSs on filtering performance; (b) distribution of the real and imaginary parts of the surface effective impedance in the presence of AFSs.

To highlight the advantages of the dynamic AFSs, the AF phenomenon generated by traditional fixed refractive index AFSs is compared in Figure 4. In Figure 4a, the dynamic AFS method is used. The dispersion characteristics of the superconductor material simultaneously regulate the host structure and the AFS, pushing the impedance matching to be satisfied in a large frequency range. For the TM wave, in the frequency range of 237~1000 THz (the relative bandwidth is 123.3%), the transmissivity is always protected above 0.9, and the angle range of the AF varies from −19.5 degrees to −76.5 degrees with noteworthy selectivity. For the TE wave, the high transmission area covers 230~1000 THz (the relative bandwidth is 125.2%), and the angle increases by 2.3~76.7 degrees. On the whole, the AF performance of the TE wave is better than that of the TM one. The former has more advantages in both frequency bandwidth and angle range. At a small angle of incidence, the electromagnetic wave leakage of the TM wave will be terrible, making the transmitted energy less than 90%. In Figure 3, when f = 500 THz, the refractive index of YaBa₂Cu₃O₇ material in AFSs is 0.8952. Therefore, when comparing in Figure 4, YaBa₂Cu₃O₇ material in AFSs is replaced with a medium with a refractive index of 0.8952 for comparison. It should be emphasized that the definition of refractive index 0.8952 here is only to highlight the advantages of AFSs in theory, rather than to actually manufacture a medium for replacement. In Figure 4b, in the case of the TM wave, the effective AF working area is attenuated to 300~545 THz, and the adjustable angle range is reduced to −39.6~−65.2 degrees. For the TE wave incidence, the corresponding performance indicators are 435~550 THz and 57.7~65.4 degrees, respectively. Substantially, under the static AFSs, the angle selection performance of the TM wave is more productive than that caused by the TE wave. Compared with Figure 4a,b, using the dynamic AFSs, the bandwidths of the TM and TE waves are 763 THz and 770 THz, respectively, while in the static AFSs, the corresponding bandwidths are 245 THz and 115 THz in turn; obviously, the former is more prominent.

It can be inferred from the above analysis that the angle selection characteristics are mainly determined by the host structure, that is, the parameter design of superconductor materials often plays a key role in the performance of the AF. To distinctly explain the influences of the thickness on the AF performance, the concept of a rectangle coefficient as the ratio of the angle range with a transmittance of −3 dB to that with a transmittance of −30 dB is defined [8].

$$RC=\frac{\Delta {\theta }_{-3\mathrm{dB}}}{\Delta {\theta }_{-30\mathrm{dB}}}$$

(10)

The value region of RC is 0~1. The closer the RC value is to one, the steeper the rectangle, the stronger the filtering ability, and the fewer interference signals. In Figure 5a, under the excitation of the TM wave, if the thickness of the superconductor layer of the host structure gradually expands to 100 nm, 1000 nm, 2000 nm, and 3000 nm, respectively, the corresponding RC rapidly improves to 0.7888, 0.9080, 0.9604, and 0.9798, respectively. However, the improvement of the RC inevitably sacrifices the transmission performance. When d_Y = 3000 nm, the transmission near the critical angle is slightly lower than 0.9. Obviously, if the thickness of the medium exceeds a certain limit, the original AFSs can no longer perfectly match the impedance of the host structure, causing energy leakage. For the TE wave, the phenomenon of thickness adjustment on the AF is similar. RC climbs with the stretching of d_Y. When d_Y is 100 nm, 1000 nm, 2000 nm, and 3000 nm, the corresponding RC is 0.7780, 0.9040, 0.9604, and 0.9813. Similarly, the enhancement of the thickness will also optimize the angle selection characteristics at the expense of the formation of transmission gaps. Specific transmission performance degradation can be seen in Figure 5b. The thickness of the host structure will correspondingly alter the angle selection characteristics, mainly because the thickness extension changes the optical path of electromagnetic wave propagation in the structure, and a good impedance matching cannot be separated from the appropriate optical path; the better the impedance matching degree, the better the angle selectivity. Therefore, the appropriate enhancement of thickness can improve RC. However, it is inevitable that the increase in thickness will also lead to a more intense resonance of electromagnetic waves, so the transmission gap will be generated near the critical angle.

The properties of the superconductor materials are obviously affected by the temperature, and naturally, the features of AF will also be operated. Considering that the superconductor materials can be viewed as lossless below the critical temperature, the temperature range of 0~85 K is selected for discussion. In Figure 6, regardless of whether the TM wave or the TE wave is incident, the transmissivity in the angle selection area is higher than 0.9 in the whole temperature variation range. This benign phenomenon is beneficial to the positive role played by the dynamic AFSs. It not only can balance the impact of frequency changes, but also apply to the temperature drifts. Under the excitation of the TM wave, as the temperature rises from 0 K to 85 K, the controllable angle range shifts from −63.2 degrees to −75.7 degrees, while under the TE one, the angle range changes from 63.5 degrees to 75.8 degrees. The manipulation of temperature can expand the angle working range of the TM and TE waves at the same time, and it is accompanied by the trend of first slow and then accelerated.

4. Conclusions

In this paper, a novel design idea is proposed to realize the AF through the ENZ characteristics of superconductor materials, which are also independent of polarization. The traditional static AFS is abandoned, and the dynamic AFS is composed of an air layer and superconductor material, which balances the effects of dispersion and temperature on AF performances. For the TM wave, the frequency bandwidth caused by using an AFS or not is 763 THz and 245 THz, respectively, and the working bandwidth is expanded by 211.4%. For the TE wave, the corresponding indicators are 770 THz, 115 THz, and 569.5% in turn. In addition, both kinds of incident waves can work normally in the range of 0~85 K and maintain transmissivity above 0.9 and a strong selectivity. The extension of the thickness of the superconductor material for improving the rectangular coefficient is also discussed. In general, the AF with ultra-wideband, polarization independence, high transmittance, and significant angle selection is realized for the first time in this paper. We hope that the proposed concept is meaningful in the development of AFs.