Convolution Error Reduction for a Fabry–Pérot-Based Linewidth Measurement: A Theoretical and Experimental Study
Abstract
1. Introduction
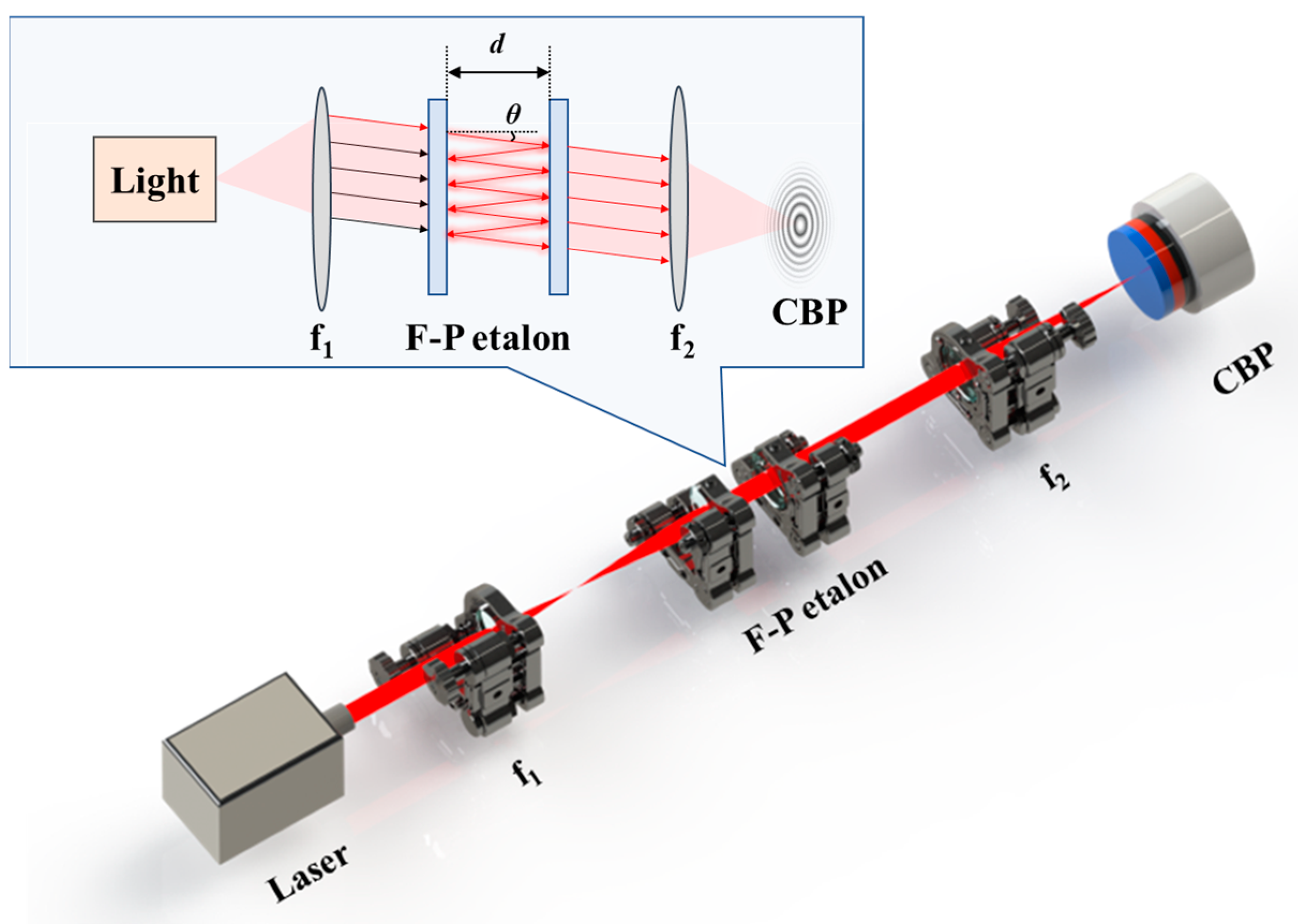
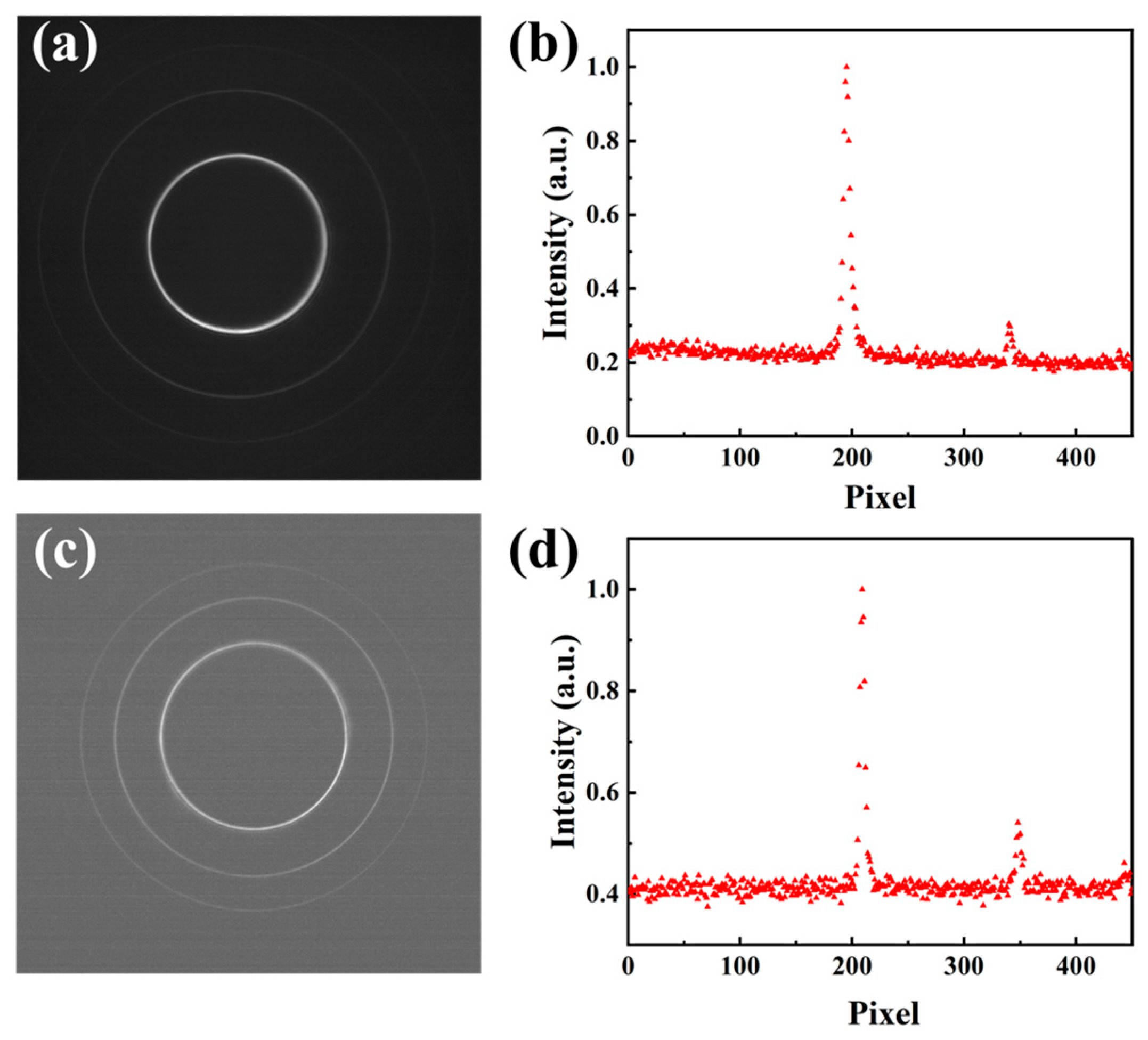
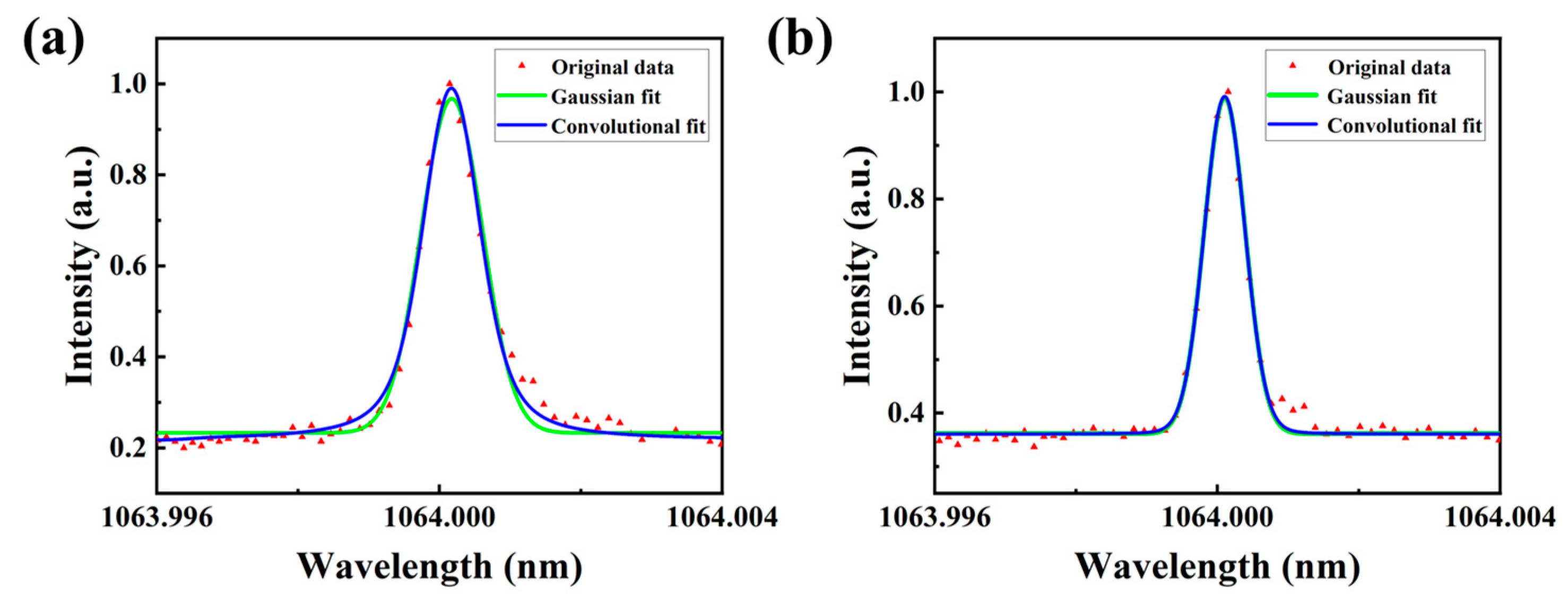
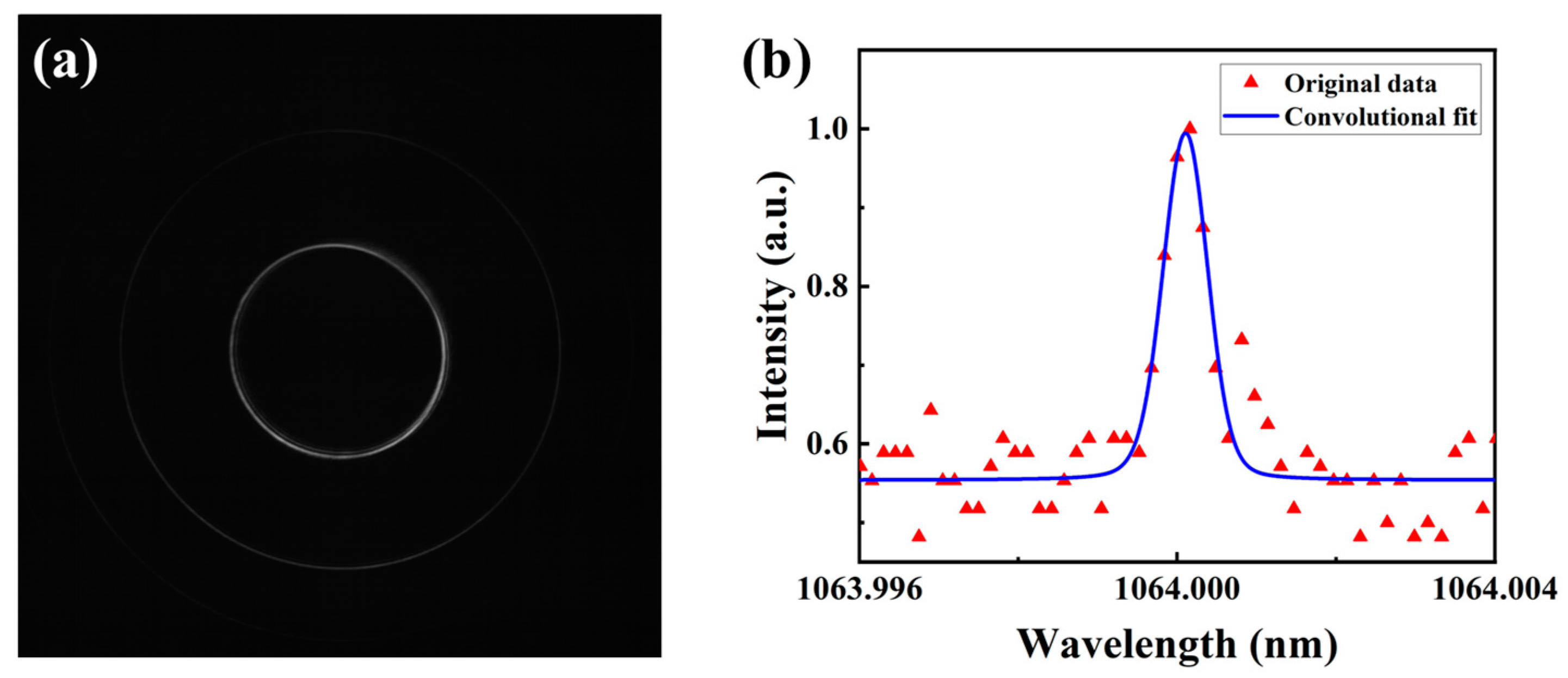
2. Experimental Setup and Gaussian Fit
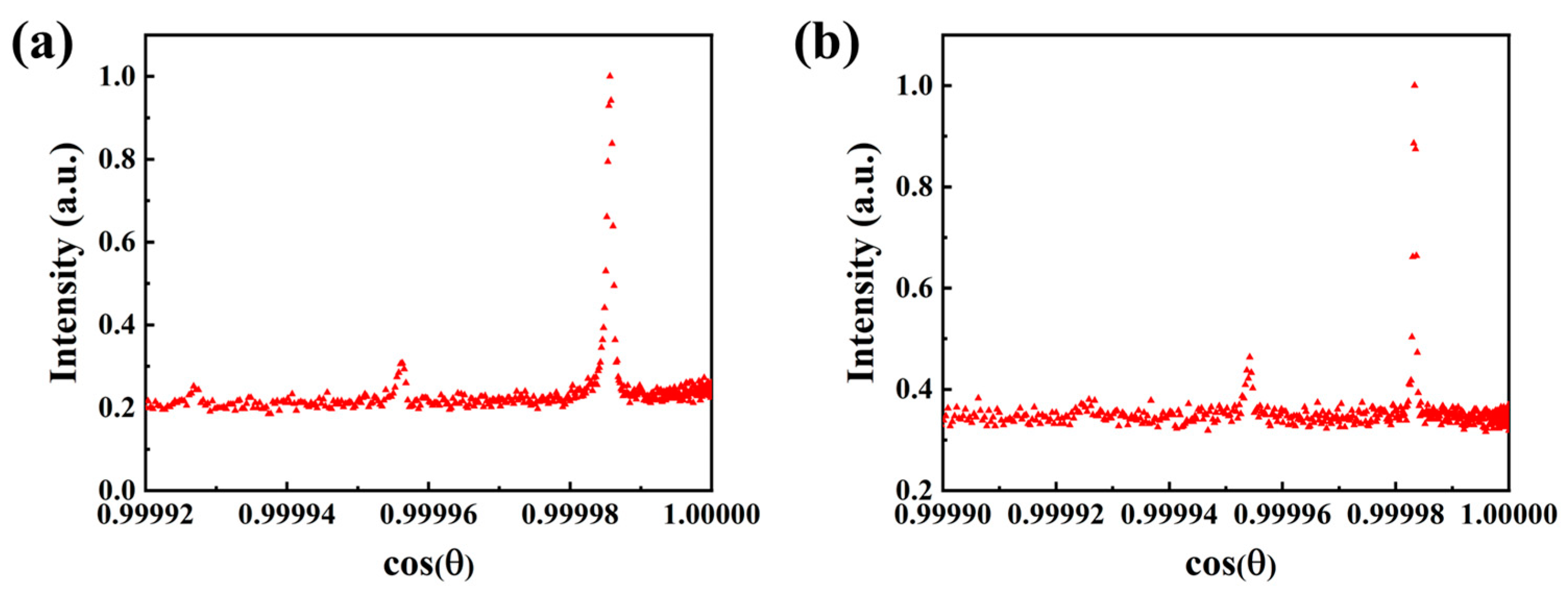
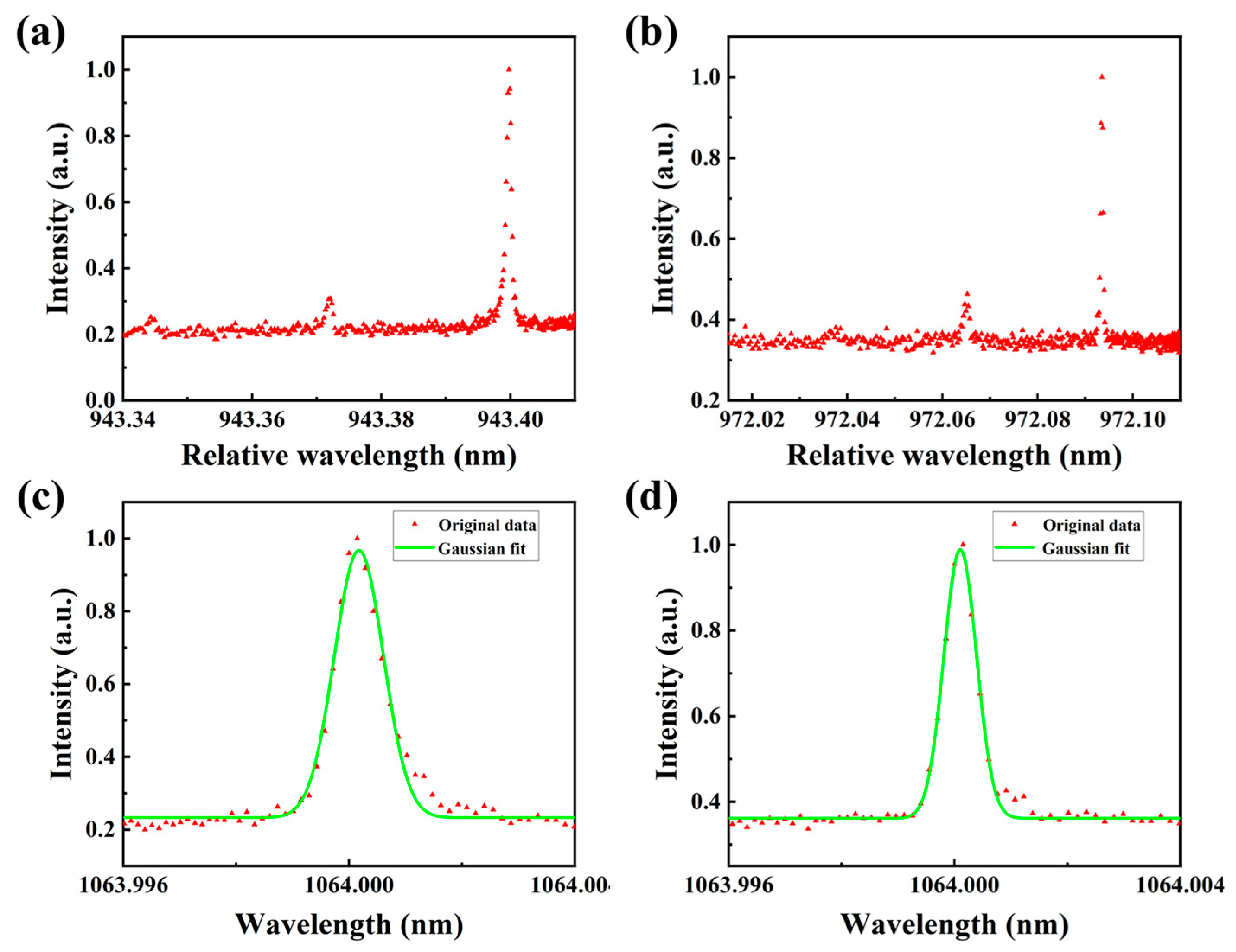
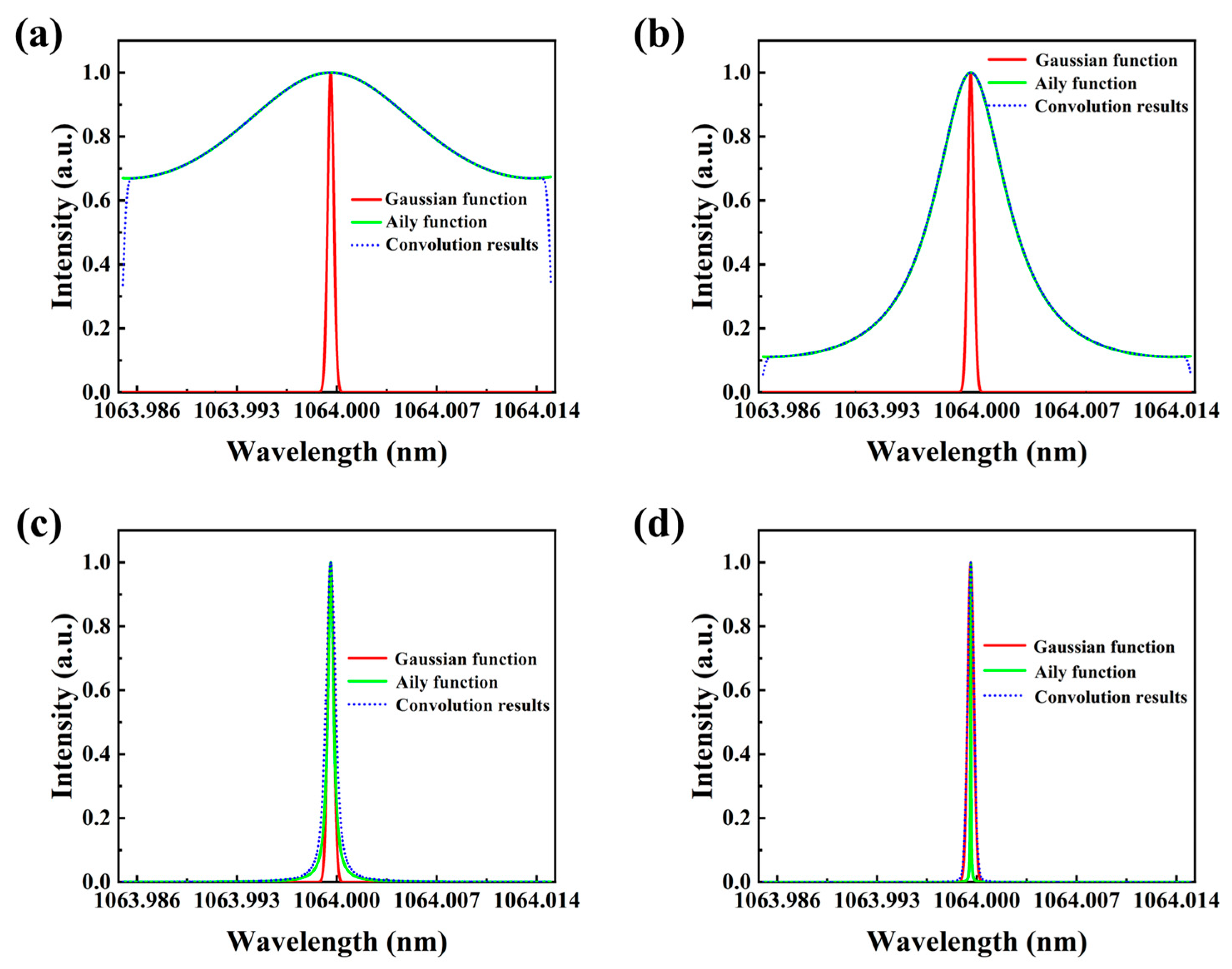
3. Analysis and Reduction of Convolution Error
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, S.; Shi, W.; Feng, Y.; Zhang, L.; Yang, Z.; Xu, S.; Zhu, X.; Norwood, R.A.; Peyghambarian, N. Review of recent progress on single-frequency fiber lasers. J. Opt. Soc. Am. B. 2017, 34, A49–A62. [Google Scholar] [CrossRef]
- Yang, X.; Bai, Z.; Chen, D.; Chen, W.; Yan, F.; Richard, P.M. Widely-tunable single-frequency diamond Raman laser. Opt. Express 2021, 29, 29449–29457. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Bai, Z.; Jin, D.; Qi, Y.; Ding, J.; Yan, B.; Wang, Y.; Lu, Z.; Mildren, R.P. Narrow laser-linewidth measurement using short delay self-heterodyne interferometry. Opt. Express 2022, 30, 30600–30610. [Google Scholar] [CrossRef] [PubMed]
- Peng, W.; Jin, P.; Li, F.; Su, J.; Lu, H.; Peng, K. A Review of the High-Power All-Solid-State Single-Frequency Continuous-Wave Laser. Micromachines 2021, 12, 1426. [Google Scholar] [CrossRef]
- Chen, H.; Bai, Z.; Yang, X.; Ding, J.; Qi, Y.; Yan, B.; Wang, Y.; Lu, Z.; Mildren, R.M. Enhanced stimulated Brillouin scattering utilizing Raman conversion in diamond. Appl. Phys. Lett. 2022, 120, 181103. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, Z.; Tian, M.; Jin, D.; Pang, Y.; Li, S.; Yan, X.; Wang, Y.; Lu, Z. A comprehensive review on the development and applications of narrow-linewidth lasers. Microw. Opt. Techn. Lett. 2022, 64, 2244–2255. [Google Scholar] [CrossRef]
- Jin, D.; Bai, Z.; Lu, Z.; Fan, R.; Zhao, Z.; Yang, X.; Wang, Y.; Mildren, R.P. 22.5-W narrow-linewidth diamond Brillouin laser at 1064 nm. Opt. Lett. 2022, 47, 5360–5363. [Google Scholar] [CrossRef]
- Guan, H.; Novack, A.; Galfsky, T.; Ma, Y.; Fathololoumi, S.; Horth, A.; Huynh, N.T.; Roman, J.; Shi, R.; Caverley, M.; et al. Widely-tunable, narrow-linewidth III-V/silicon hybrid external-cavity laser for coherent communication. Opt. Express 2018, 26, 7920–7933. [Google Scholar] [CrossRef]
- Zhou, K.; Zhao, Q.; Huang, X.; Yang, C.; Li, C.; Zhou, E.; Xu, X.; Wong, K.Y.; Cheng, H.; Gan, J.; et al. kHz-order linewidth controllable 1550 nm single-frequency fiber laser for coherent optical communication. Opt. Express 2017, 25, 19752–19759. [Google Scholar] [CrossRef]
- Sheng, Q.; Ma, H.; Li, R.; Wang, M.; Shi, W.; Yao, J. Recent progress on narrow-linewidth crystalline bulk Raman lasers. Results Phys. 2020, 17, 103073. [Google Scholar] [CrossRef]
- Arpita, S.R.; Pradeep, K.K. Brillouin-induced self-heterodyne method for low jitter measurement of laser linewidth. J. Opt. Soc. Am. B. 2019, 36, 3145–3150. [Google Scholar]
- Gao, J.; Jiao, D.; Deng, X.; Liu, J.; Zhang, L.; Zang, Q.; Zhang, X.; Liu, T.; Zhang, S. A Polarization-Insensitive Recirculating Delayed Self-Heterodyne Method for Sub-Kilohertz Laser Linewidth Measurement. Photonics 2021, 8, 137. [Google Scholar] [CrossRef]
- Xue, M.; Zhao, J. Laser linewidth measurement based on long and short delay fiber combination. Opt. Express 2021, 29, 27118–27126. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Zhu, T.; Liu, M.; Huang, W. Precise measurement of ultra-narrow laser linewidths using the strong coherent envelope. Sci. Rep.-UK 2017, 7, 41988. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Ke, C.; Zhong, Y.; Xing, C.; Wang, H.; Yang, K.; Cui, S.; Liu, D. Ultra-narrow-linewidth measurement utilizing dual-parameter acquisition through partially coherent light interference. Opt. Express 2020, 28, 8484–8493. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, Z.; Qi, Y.; Ding, J.; Li, S.; Yang, X.; Wang, Y.; Lu, Z. Narrow-Linewidth Laser Linewidth Measurement Technology. Front. Phys. 2021, 9, 768165. [Google Scholar] [CrossRef]
- Peng, Y. A Novel Scheme for Hundred-Hertz Linewidth Measurements with the Self-Heterodyne Method. Chin. Phys. Lett. 2013, 30, 084208. [Google Scholar] [CrossRef]
- Gao, W.; Lu, Z.; He, W.; Dong, Y.; Hasi, W. Characteristics of amplified spectrum of a weak frequency-detuned signal in a Brillouin amplifier. Laser Part Beams 2009, 2, 465–470. [Google Scholar] [CrossRef]
- Xue, J.; Chen, W.; Pan, Y.; Shi, J.; Fang, Y.; Xie, H.; Xie, M.; Sun, L.; Su, B. Pulsed laser linewidth measurement using Fabry–Pérot scanning interferometer. Results Phys. 2016, 6, 698–703. [Google Scholar] [CrossRef]
- Ma, Y.; Yu, Y.; Li, H.; Huang, J.; Yao, Y.; Zhou, B.; Fang, Y.; Min, J.; Liang, K. Accurate measurement of high resolution spectrum obtained by F–P etalon and ICCD. Appl. Phys. B-Lasers O 2014, 116, 575–584. [Google Scholar] [CrossRef]
- Yao, Y.; Niu, Q.; Liang, K. Measurement error analysis of Brillouin lidar system using F–P etalon and ICCD. Opt. Commun. 2016, 375, 58–62. [Google Scholar] [CrossRef]
- Huang, J.; Ma, Y.; Zhou, B.; Li, H.; Yu, Y.; Liang, K. Processing method of spectrum measurement using FP etalon and ICCD. Opt. Express 2012, 20, 18568–18578. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, D.; Yang, Z.; Shi, J.; Liu, D.; Gong, W.; Fry, E.S. Experimental investigation on line width compression of stimulated Brillouin scattering in water. Appl. Phys. Lett. 2011, 98, 221106. [Google Scholar] [CrossRef]
- Toshihiko, T.; Kenichi, I.; Toshiharu, T. Linewidth Measurement of a Single Longitudinal Mode AlGaAs Laser with a Fabry-Perot Interferometer. Jpn. J. Appl. Phys. 1980, 19, L725–L727. [Google Scholar]
- Jakup, R.; Bostjan, B. Injection-locked range and linewidth measurements at different seed-laser linewidths using a Fabry–Pérot laser-diode. Opt. Quant. Electron. 2018, 50, 502. [Google Scholar]
- George, H.M.; Edward, I.M.; Craig, R.W. The national ignition facility. Opt. Eng. 2004, 43, 2841–2853. [Google Scholar]
- John, D.L.; Peter, A.; Richard, L.B.; Glendinning, S.G.; Siegfried, H.G.; Steven, W.H.; Robert, L.K.; Otto, L.L.; Laurence, J.S. The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Phys. Plasmas 2004, 11, 339–491. [Google Scholar]
- Zheng, W.; Wei, X.; Zhu, Q.; Jing, F.; Hu, D.; Su, J.; Zheng, K.; Yuan, X.; Zhou, X.; Dai, W.; et al. Laser performance of the SG-III laser facility. High Power Laser Sci. 2016, 4, e21. [Google Scholar] [CrossRef]
- Ma, Y.; Li, H.; Yu, Y.; Yao, Y.; Fang, Y.; Zhou, B.; Huang, J.; Min, J.; Liang, K. Experimental analysis on calibration of instrument broadening in a lidar system with Fabry–Perot etalon. J. Mod. Optic 2013, 60, 1967–1975. [Google Scholar] [CrossRef]
- Hun, X.; Bai, Z.; Chen, B.; Wang, J.; Cui, C.; Qi, Y.; Ding, J.; Wang, Y.; Lu, Z. Fabry–Pérot based short pulsed laser linewidth measurement with enhanced spectrum resolution. Results Phys. 2022, 37, 105510. [Google Scholar] [CrossRef]
- Zhao, Z.; Bai, Z.; Jin, D.; Chen, X.; Qi, Y.; Ding, J.; Yan, B.; Wang, Y.; Lu, Z.; Mildren, R.P. The Influence of Noise Floor on the Measurement of Laser Linewidth Using Short-Delay-Length Self-Heterodyne/Homodyne Techniques. Micromachines 2022, 13, 1311. [Google Scholar] [CrossRef]
- Chen, B.; Bai, Z.; Zhao, G.; Zhang, Y.; Yan, B.; Qi, Y.; Ding, J.; Wang, K.; Wang, Y.; Lu, Z. Compound Cavity Passively Q-Switched Single-Longitudinal-Mode Diode-Pumped Laser. Front. Phys. 2022, 10, 820177. [Google Scholar] [CrossRef]
- Jin, D.; Bai, Z.; Wang, Q.; Chen, Y.; Liu, Z.; Fan, R.; Qi, Y.; Ding, J.; Yang, X.; Wang, Y.; et al. Doubly Q-switched single longitudinal mode Nd:YAG laser with electro-optical modulator and Cr4+:YAG. Opt. Commun. 2020, 463, 125500. [Google Scholar] [CrossRef]
- Xue, F.; Zhang, S.; Cong, Z.; Huang, Q.; Guan, G.; Wu, Q.; Chen, H.; Bai, F.; Liu, Z. Diode-end-pumped single-longitudinal-mode passively Q-switched Nd: GGG laser. Laser Phys. Lett. 2018, 15, 035001. [Google Scholar] [CrossRef]
- Liang, K.; Ma, Y.; Huang, J.; Li, H.; Yu, Y. Precise measurement of Brillouin scattering spectrum in the ocean using F–P etalon and ICCD. Appl. Phys. B-Lasers O 2011, 105, 421. [Google Scholar] [CrossRef]
| Reflectance | TSW | Linewidth of Gaussian Fitting (Γ1) | Residuals of Gaussian Fitting | Linewidth of Convolutional Fitting (Γ2) | Residuals of Convolutional Fitting | Difference (Γ1-Γ2) |
|---|---|---|---|---|---|---|
| R = 95% | 122 MHz | MHz | 0.0584 nm | MHz | 0.0317 nm | 89.5 MHz |
| R = 99.5% | 9.6 MHz | MHz | 0.01 nm | MHz | 0.0092 nm | 7.1 MHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hun, X.; Bai, Z.; Wang, J.; Chen, B.; Cui, C.; Wang, Y.; Lu, Z. Convolution Error Reduction for a Fabry–Pérot-Based Linewidth Measurement: A Theoretical and Experimental Study. Photonics 2022, 9, 1004. https://doi.org/10.3390/photonics9121004
Hun X, Bai Z, Wang J, Chen B, Cui C, Wang Y, Lu Z. Convolution Error Reduction for a Fabry–Pérot-Based Linewidth Measurement: A Theoretical and Experimental Study. Photonics. 2022; 9(12):1004. https://doi.org/10.3390/photonics9121004
Chicago/Turabian StyleHun, Xuanning, Zhenxu Bai, Jianping Wang, Bin Chen, Can Cui, Yulei Wang, and Zhiwei Lu. 2022. "Convolution Error Reduction for a Fabry–Pérot-Based Linewidth Measurement: A Theoretical and Experimental Study" Photonics 9, no. 12: 1004. https://doi.org/10.3390/photonics9121004
APA StyleHun, X., Bai, Z., Wang, J., Chen, B., Cui, C., Wang, Y., & Lu, Z. (2022). Convolution Error Reduction for a Fabry–Pérot-Based Linewidth Measurement: A Theoretical and Experimental Study. Photonics, 9(12), 1004. https://doi.org/10.3390/photonics9121004






