Photonic Crystal Fiber Sensor for Detecting Sulfuric Acid in Different Concentrations
Abstract
:1. Introduction
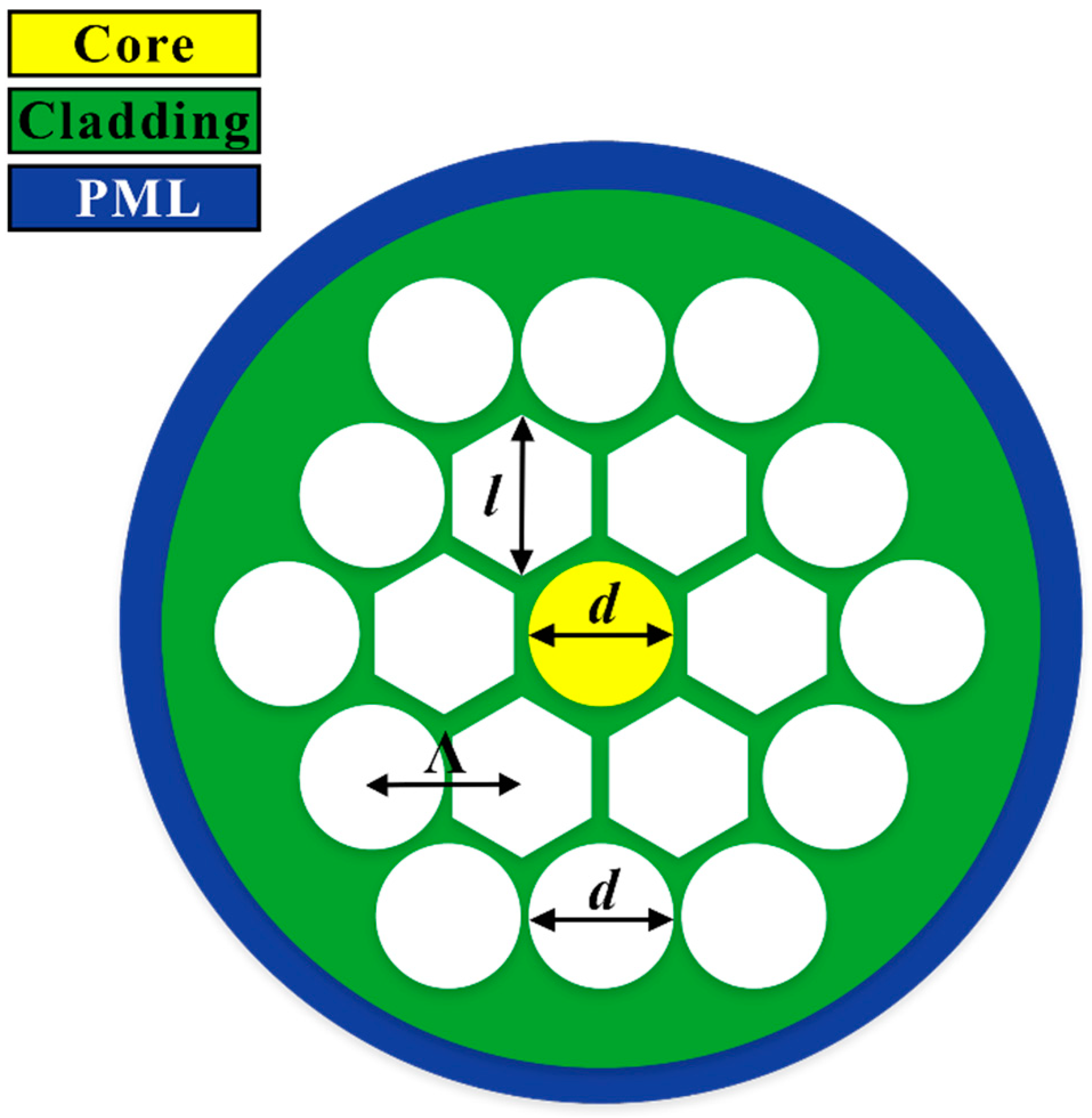
2. Design
3. Methodology
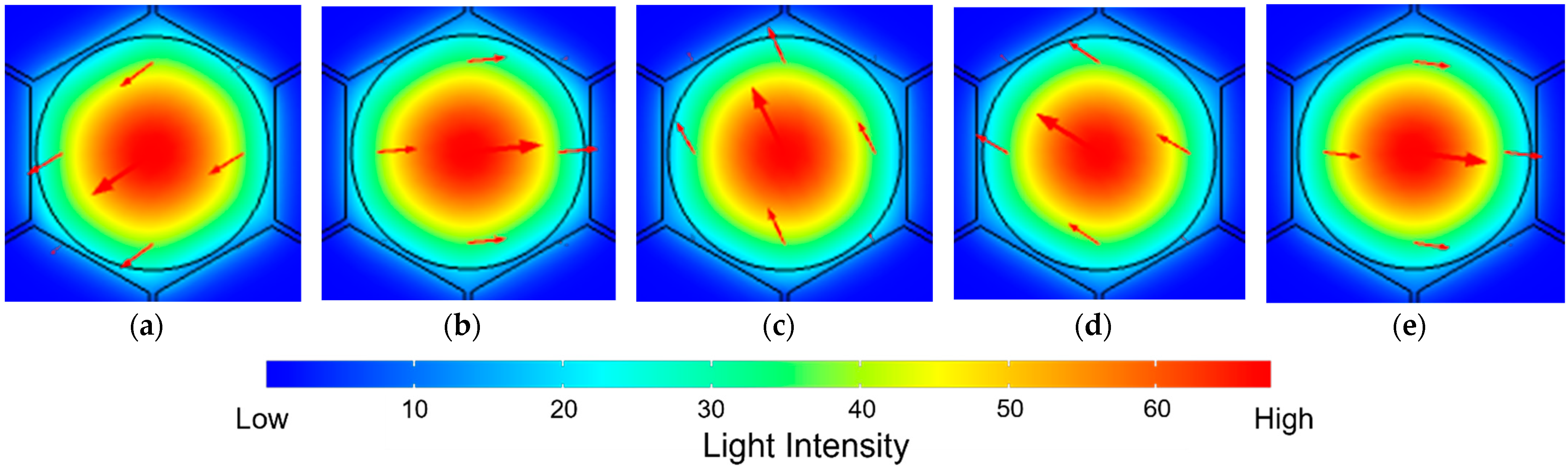
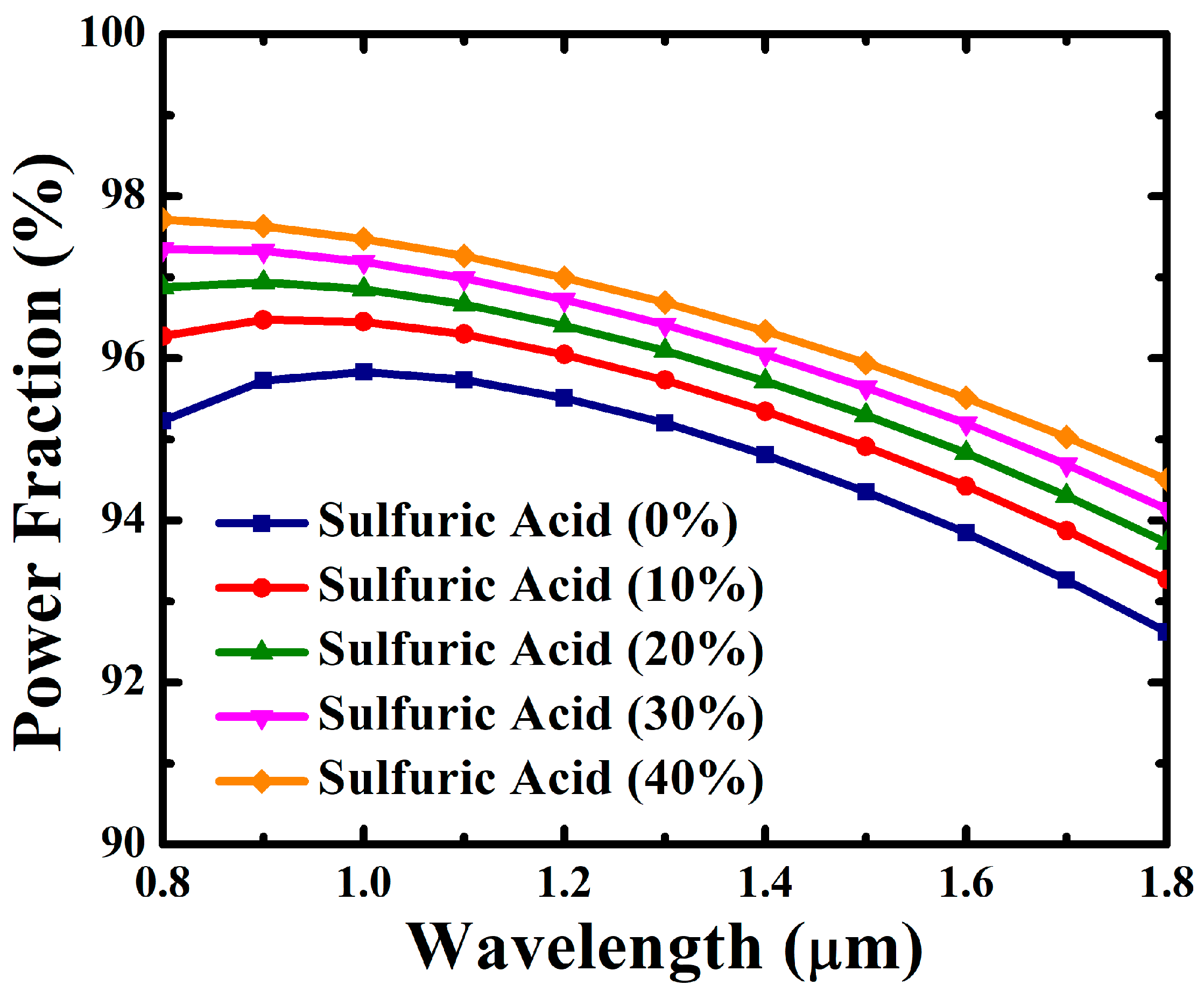
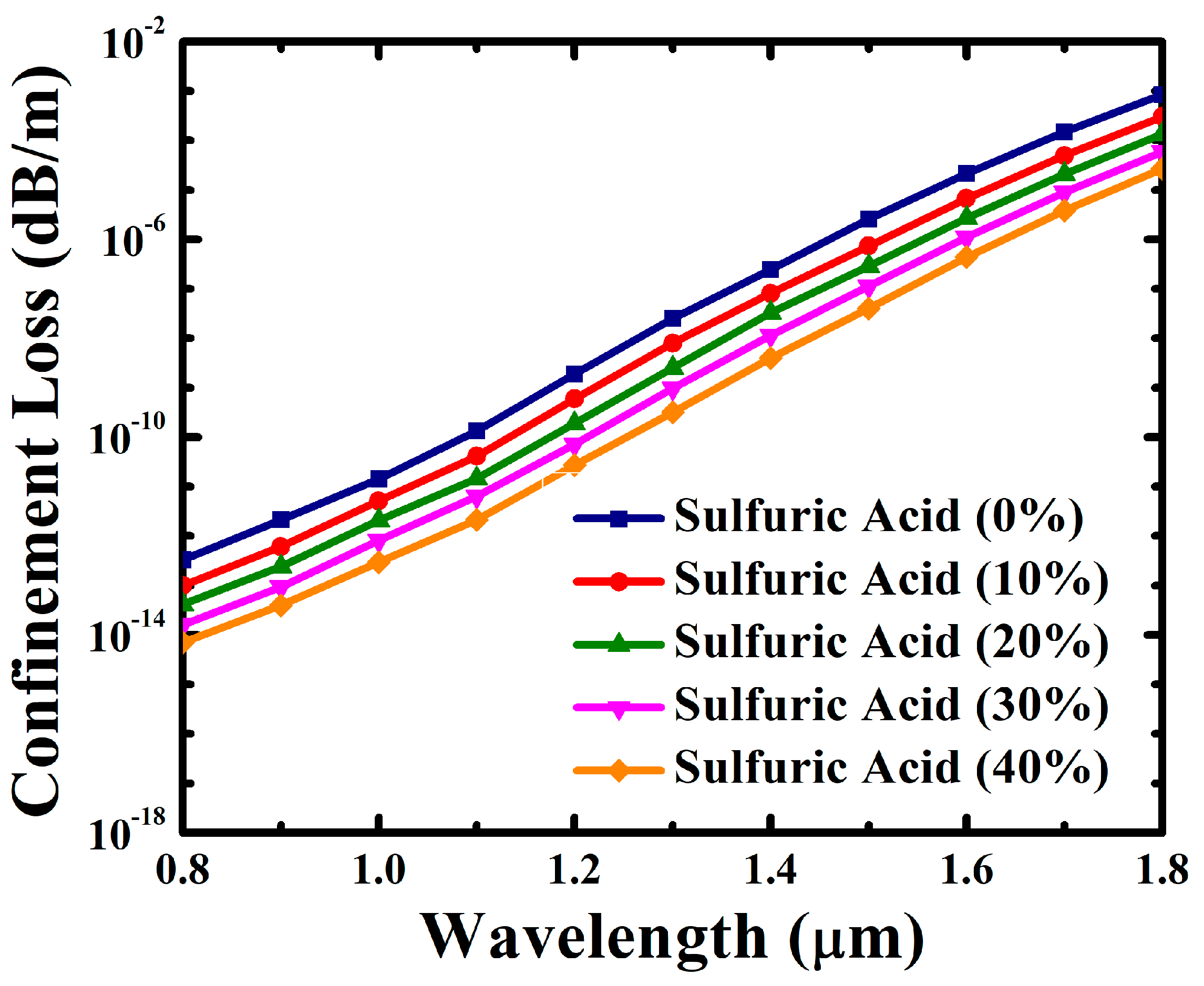
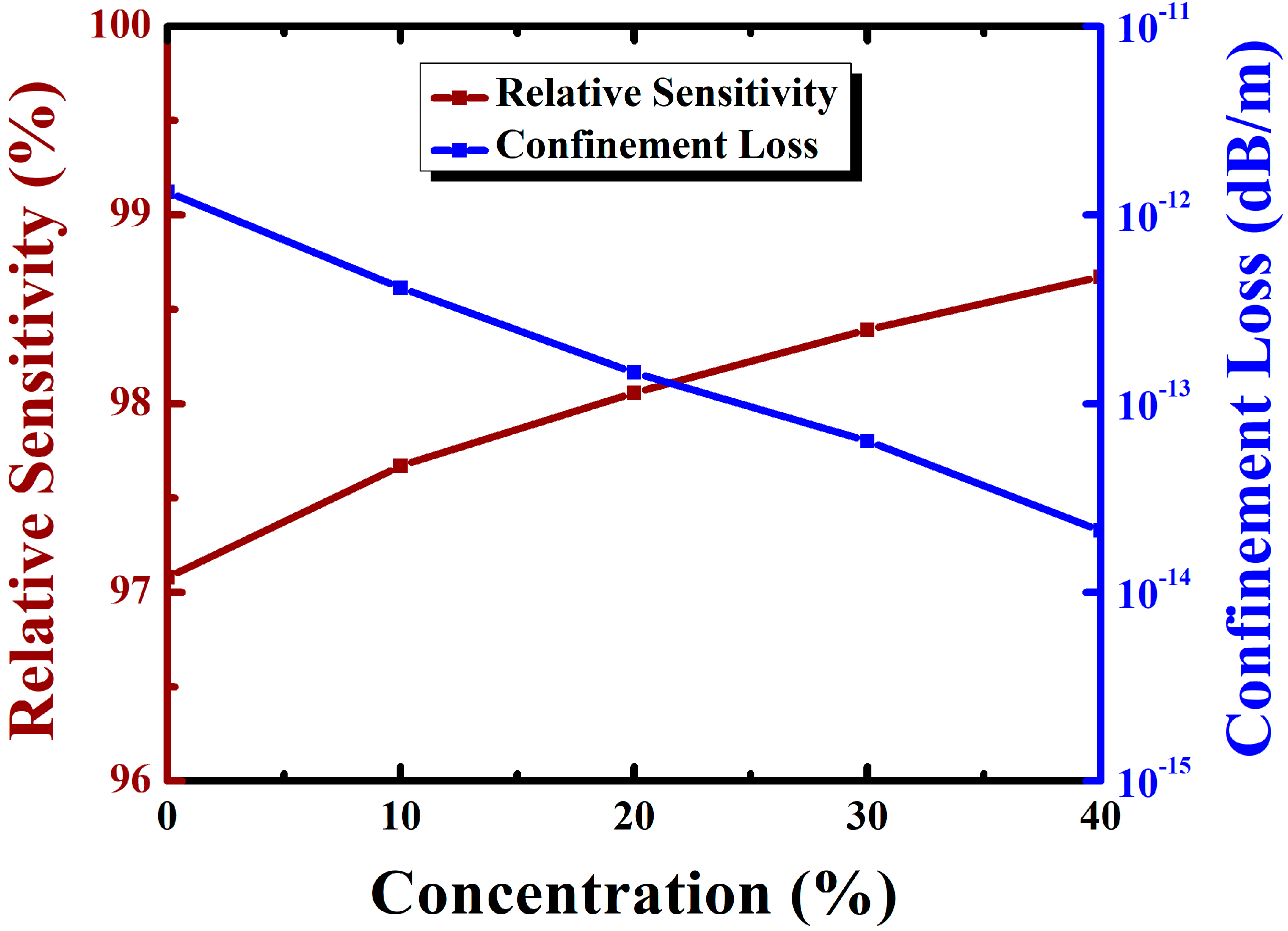
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hansen, T.P.; Broeng, J.; Libori, S.E.B.; Knudsen, E.; Bjarklev, A.; Jensen, J.R.; Simonsen, H. Highly birefringent index-guiding photonic crystal fibers. IEEE Photonics Technol. Lett. 2001, 13, 588–590. [Google Scholar] [CrossRef] [Green Version]
- Reeves, W.; Knight, J.; Russell, P.; Roberts, P. Demonstration of ultra-flattened dispersion in photonic crystal fibers. Opt. Express 2002, 10, 609. [Google Scholar] [CrossRef]
- Habib, M.A.; Anower, M.S.; Hasan, M.R. Ultrahigh birefringence and extremely low loss slotted-core microstructure fiber in terahertz regime. Curr. Opt. Photonics 2017, 1, 567–572. [Google Scholar] [CrossRef]
- Pinto, A.M.R.; Lopez-Amo, M. Photonic crystal fibers for sensing applications. J. Sens. 2012, 2012, 598178. [Google Scholar] [CrossRef] [Green Version]
- Troia, B.; Paolicelli, A.; De, F.; Passaro, V.M.N. Photonic Crystals for Optical Sensing: A Review. In Advances in Photonic Crystals; IntechOpen: Rijeka, Croatia, 2013. [Google Scholar] [CrossRef] [Green Version]
- Gahir, H.K.; Khanna, D. Design and development of a temperature-compensated fiber optic polarimetric pressure sensor based on photonic crystal fiber at 1550 nm. Appl. Opt. 2007, 46, 1184–1189. [Google Scholar] [CrossRef]
- Rifat, A.A.; Ahmed, K.; Asaduzzaman, S.; Paul, B.K.; Ahmed, R. Development of photonic crystal fiber-based gas/chemical sensors. In Computational Photonic Sensors; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef] [Green Version]
- Martynkien, T.; Szpulak, M.; Urbanczyk, W. Modeling and measurement of temperature sensitivity in birefringent photonic crystal holey fibers. Appl. Opt. 2005, 44, 7780–7788. [Google Scholar] [CrossRef]
- Bock, W.J.; Jiahua, C.; Eftimov, T.; Urbanczyk, W. A photonic crystal fiber sensor for pressure measurements. In Proceedings of the IMTC 2005—Instrumentation and Measurement Technology Conference, Ottawa, ON, Canada, 17–19 May 2005; Volume 2, pp. 1177–1181. [Google Scholar] [CrossRef]
- Asaduzzaman, S.; Ahmed, K. Proposal of a gas sensor with high sensitivity, birefringence and nonlinearity for air pollution monitoring. Sens. Bio-Sens. Res. 2016, 10, 20–26. [Google Scholar] [CrossRef]
- Asaduzzaman, S.; Ahmed, K.; Bhuiyan, T.; Farah, T. Hybrid photonic crystal fiber in chemical sensing. Springerplus 2016, 5, 748. [Google Scholar] [CrossRef] [Green Version]
- Leon, M.J.B.M.; Kabir, M.A. Design of a liquid sensing photonic crystal fiber with high sensitivity, bireferingence & low confinement loss. Sens. Bio-Sens. Res. 2020, 28, 100335. [Google Scholar] [CrossRef]
- Niger, M.; Hasin, T.F.; Nizami, M.A.F.; Rafee, M.A. Three Modified Structures of Photonic Crystal Fiber for Estimation of Sulfuric Acid Concentration with Low Confinement Loss and Negative Dispersion. In Proceedings of the 2019 4th International Conference on Electrical Information and Communication Technology (EICT 2019), Baku, Azerbaijan, 20–22 December 2019. [Google Scholar] [CrossRef]
- Fraenkel, D. Structure and ionization of sulfuric acid in water. New J. Chem. 2015, 39, 5124–5136. [Google Scholar] [CrossRef]
- Islam, S.; Kumar, B.; Ahmed, K. Liquid-infiltrated photonic crystal fiber for sensing purpose: Design and analysis. Alex. Eng. J. 2018, 57, 1459–1466. [Google Scholar] [CrossRef]
- Podder, E.; Hossain, M.B.; Jibon, R.H.; Bulbul, A.A.M.; Mondal, H.S. Chemical sensing through photonic crystal fiber: Sulfuric acid detection. Front. Optoelectron. 2019, 12, 372–381. [Google Scholar] [CrossRef]
- Caroline, B.E.; Umamaheswari, P.; Jayasri, R.; Kumar, D.S. Investigation on the detection of sulfuric acid using photonic crystal fiber sensor. In Proceedings of the 2020 7th International Conference on Smart Structures and Systems (ICSSS 2020), Chennai, India, 21–24 July 2020. [Google Scholar] [CrossRef]
- Maidi, A.M.; Yakasai, I.; Abas, P.E.; Nauman, M.M.; Apong, R.A.; Kaijage, S.; Begum, F. Design and Simulation of Photonic Crystal Fiber for Liquid Sensing. Photonics 2021, 8, 16. [Google Scholar] [CrossRef]
- Eid, M.M.A.; Habib, A.; Anower, S.; Nabih, A.; Rashed, Z. Highly sensitive nonlinear photonic crystal fiber based sensor for chemical sensing applications Highly sensitive nonlinear photonic crystal fiber based sensor for chemical sensing applications. Microsyst. Technol. 2020, 27, 1007–1014. [Google Scholar] [CrossRef]
- Amouzad Mahdiraji, G.; Chow, D.M.; Sandoghchi, S.R.; Amirkhan, F.; Dermosesian, E.; Yeo, K.S.; Kakaei, Z.; Ghomeishi, M.; Poh, S.Y.; Yu Gang, S.; et al. Challenges and Solutions in Fabrication of Silica-Based Photonic Crystal Fibers: An Experimental Study. Fiber Integr. Opt. 2014, 33, 85–104. [Google Scholar] [CrossRef]
- Algorri, J.; Zografopoulos, D.; Tapetado, A.; Poudereux, D.; Sánchez-Pena, J. Infiltrated Photonic Crystal Fibers for Sensing Applications. Sensors 2018, 18, 4263. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.M.; Lai, Y.; Yuan, W.; Seah, Y.P.; Shum, P.P.; Yu, X.; Wei, H. Laser-assisted lateral optical fiber processing for selective infiltration. Opt. Express 2014, 22, 2675. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical Constants of Water in the 200-nm to 200-μm Wavelength Region. Appl. Opt. 1973, 12, 555. [Google Scholar] [CrossRef] [Green Version]
- Krieger, U.K.; Mössinger, J.C.; Luo, B.; Weers, U.; Peter, T. Measurement of the refractive indices of H2SO4–HNO3–H2O solutions to stratospheric temperatures. Appl. Opt. 2000, 39, 3691. [Google Scholar] [CrossRef] [Green Version]
- Akowuah, E.K.; Gorman, T.; Ademgil, H.; Haxha, S.; Robinson, G.K.; Oliver, J.V. Numerical Analysis of a Photonic Crystal Fiber for Biosensing Applications. IEEE J. Quantum Electron. 2012, 48, 1403–1410. [Google Scholar] [CrossRef]
- Yakasai, I.; Abas, P.E.; Kaijage, S.F.; Caesarendra, W.; Begum, F. Proposal for a quad-elliptical photonic crystal fiber for terahertz wave guidance and sensing chemical warfare liquids. Photonics 2019, 6, 78. [Google Scholar] [CrossRef] [Green Version]
- Yakasai, I.K.; Abas, P.E.; Ali, S.; Begum, F. Modelling and simulation of a porous core photonic crystal fibre for terahertz wave propagation. Opt. Quantum Electron. 2019, 51, 122. [Google Scholar] [CrossRef]
- Maidi, A.M.; Abas, P.E.; Petra, P.I.; Kaijage, S.; Zou, N.; Begum, F. Theoretical Considerations of Photonic Crystal Fiber with All Uniform-Sized Air Holes for Liquid Sensing. Photonics 2021, 8, 249. [Google Scholar] [CrossRef]
- Begum, F.; Namihira, Y.; Razzak, S.M.A.; Kaijage, S.F.; Hai, N.H.; Miyagi, K.; Higa, H.; Zou, N. Flattened chromatic dispersion in square photonic crystal fibers with low confinement losses. Opt. Rev. 2009, 16, 54–58. [Google Scholar] [CrossRef]
- Begum, F.; Namihira, Y.; Kinjo, T.; Kaijage, S. Supercontinuum generation in photonic crystal fibres at 1.06, 1.31, and 1.55 µm wavelengths. Electron. Lett. 2010, 46, 1518. [Google Scholar] [CrossRef]
- Begum, F.; Abas, P.E. Near infrared supercontinuum generation in silica based photonic crystal fiber. Prog. Electromagn. Res. C 2019, 89, 149–159. [Google Scholar] [CrossRef] [Green Version]
- Priya, K.R.; Raja, A.S.; Sundar, D.S. Design of a dual-core liquid-filled photonic crystal fiber coupler and analysis of its optical characteristics. J. Opt. Technol. 2016, 83, 569. [Google Scholar] [CrossRef]
- Hossain, M.M.; Hossain, M.B.; Amin, M.Z. Small coupling length with a low confinement loss dual-core liquid infiltrated photonic crystal fiber coupler. OSA Contin. 2018, 1, 953. [Google Scholar] [CrossRef]
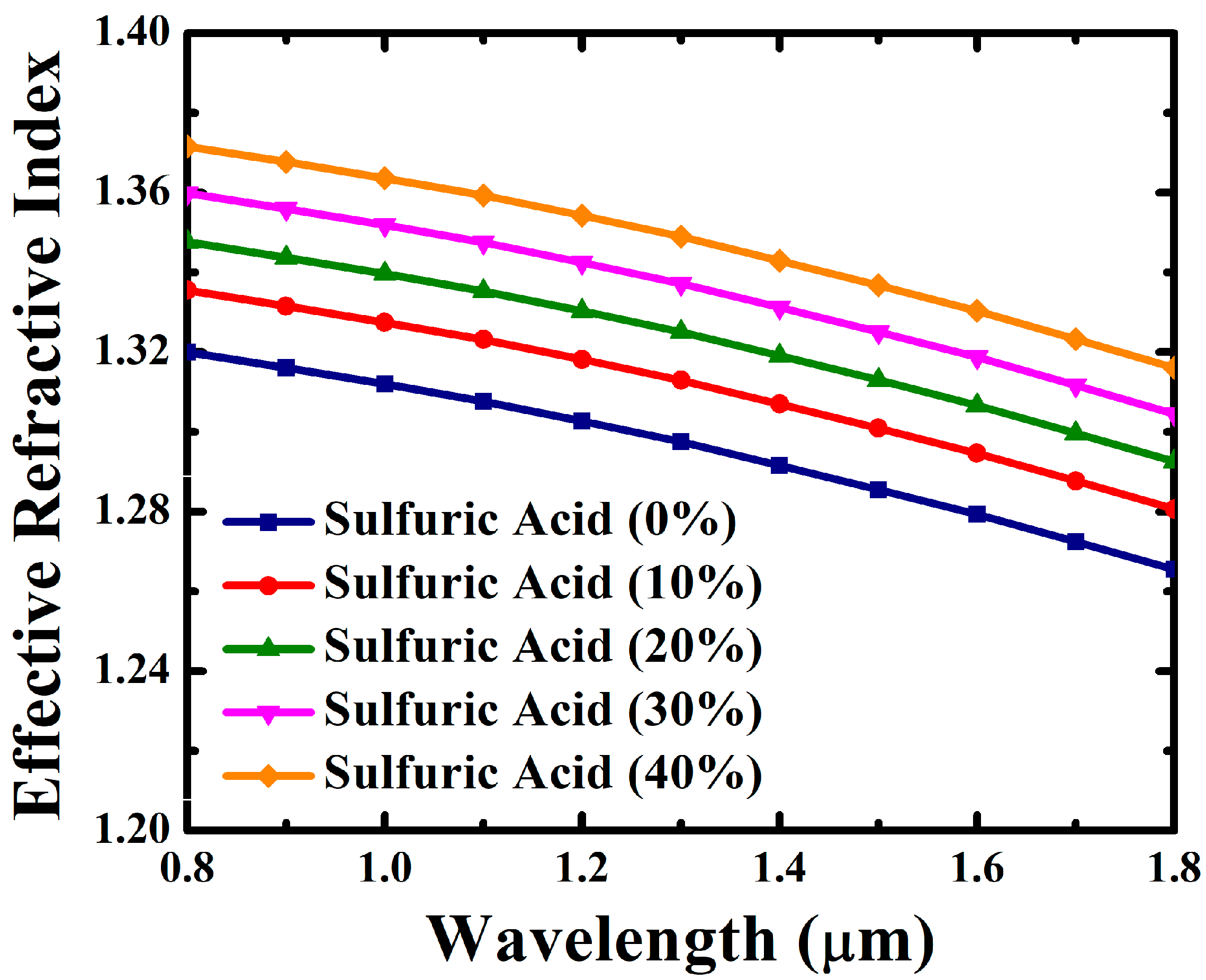



| Wavelength (µm) | Refractive Index of Sulfuric Acid in Different Concentrations | ||||
|---|---|---|---|---|---|
| 0% | 10% | 20% | 30% | 40% | |
| 0.8 | 1.3290 | 1.3451 | 1.3576 | 1.3701 | 1.3821 |
| 0.9 | 1.3280 | 1.3440 | 1.3565 | 1.3690 | 1.3810 |
| 1.0 | 1.3270 | 1.3430 | 1.3555 | 1.3680 | 1.3800 |
| 1.1 | 1.3260 | 1.3420 | 1.3545 | 1.3670 | 1.3790 |
| 1.2 | 1.3245 | 1.3405 | 1.3530 | 1.3655 | 1.3775 |
| 1.3 | 1.3230 | 1.3390 | 1.3515 | 1.3640 | 1.3760 |
| 1.4 | 1.3210 | 1.3370 | 1.3495 | 1.3620 | 1.3740 |
| 1.5 | 1.3190 | 1.3350 | 1.3475 | 1.3600 | 1.3720 |
| 1.6 | 1.3170 | 1.3330 | 1.3455 | 1.3580 | 1.3700 |
| 1.7 | 1.3145 | 1.3305 | 1.3430 | 1.3555 | 1.3675 |
| 1.8 | 1.3120 | 1.3280 | 1.3405 | 1.3530 | 1.3650 |
| Change in Dimension | Relative Sensitivity (%) | ||||
|---|---|---|---|---|---|
| 0% H2SO4 | 10% H2SO4 | 20% H2SO4 | 30% H2SO4 | 40% H2SO4 | |
| +0.1 µm | 97.04 | 97.65 | 98.04 | 98.38 | 98.66 |
| Optimum | 97.08 | 97.67 | 98.06 | 98.39 | 98.67 |
| −0.1 µm | 97.11 | 97.69 | 98.07 | 98.40 | 98.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maidi, A.M.; Kalam, M.A.; Begum, F. Photonic Crystal Fiber Sensor for Detecting Sulfuric Acid in Different Concentrations. Photonics 2022, 9, 958. https://doi.org/10.3390/photonics9120958
Maidi AM, Kalam MA, Begum F. Photonic Crystal Fiber Sensor for Detecting Sulfuric Acid in Different Concentrations. Photonics. 2022; 9(12):958. https://doi.org/10.3390/photonics9120958
Chicago/Turabian StyleMaidi, Abdul Mu’iz, Md. Abul Kalam, and Feroza Begum. 2022. "Photonic Crystal Fiber Sensor for Detecting Sulfuric Acid in Different Concentrations" Photonics 9, no. 12: 958. https://doi.org/10.3390/photonics9120958
APA StyleMaidi, A. M., Kalam, M. A., & Begum, F. (2022). Photonic Crystal Fiber Sensor for Detecting Sulfuric Acid in Different Concentrations. Photonics, 9(12), 958. https://doi.org/10.3390/photonics9120958






