Mid-Infrared Continuous Varifocal Metalens with Adjustable Intensity Based on Phase Change Materials
Abstract
:1. Introduction
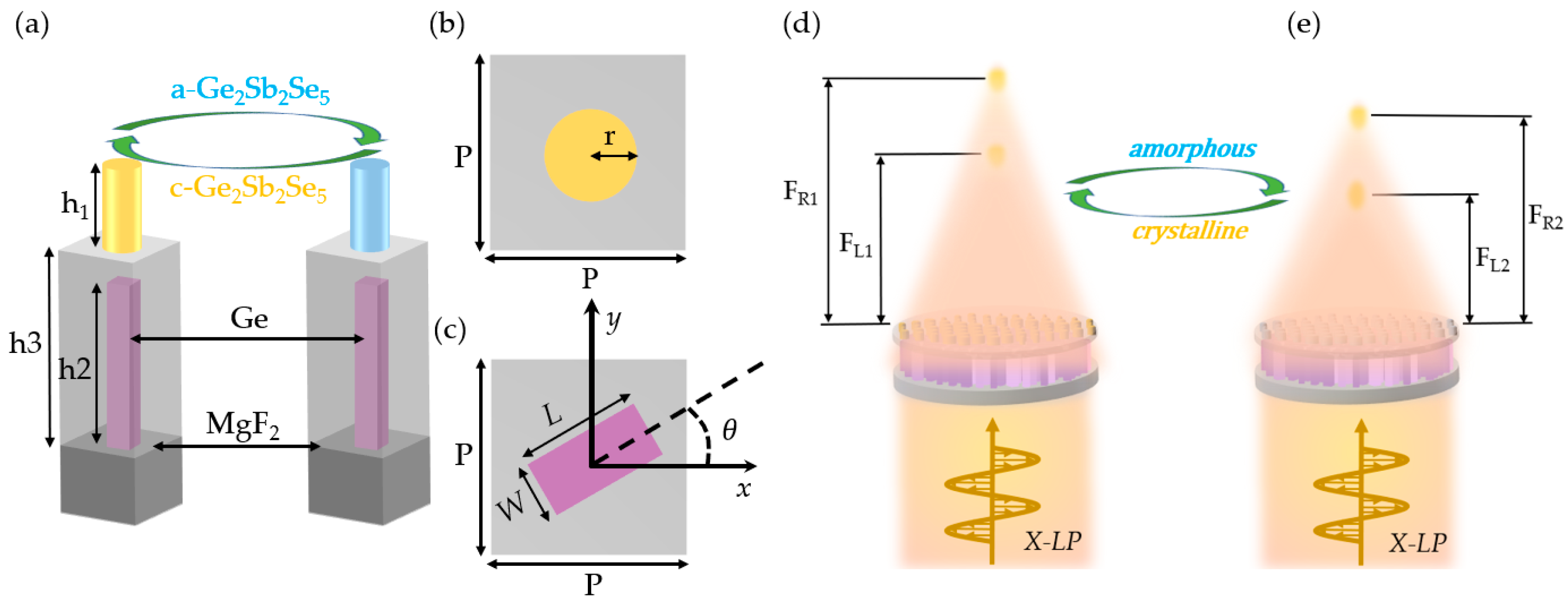
2. Unit Structure and Principle of the Bilayer Metalens
3. Results and Discussion
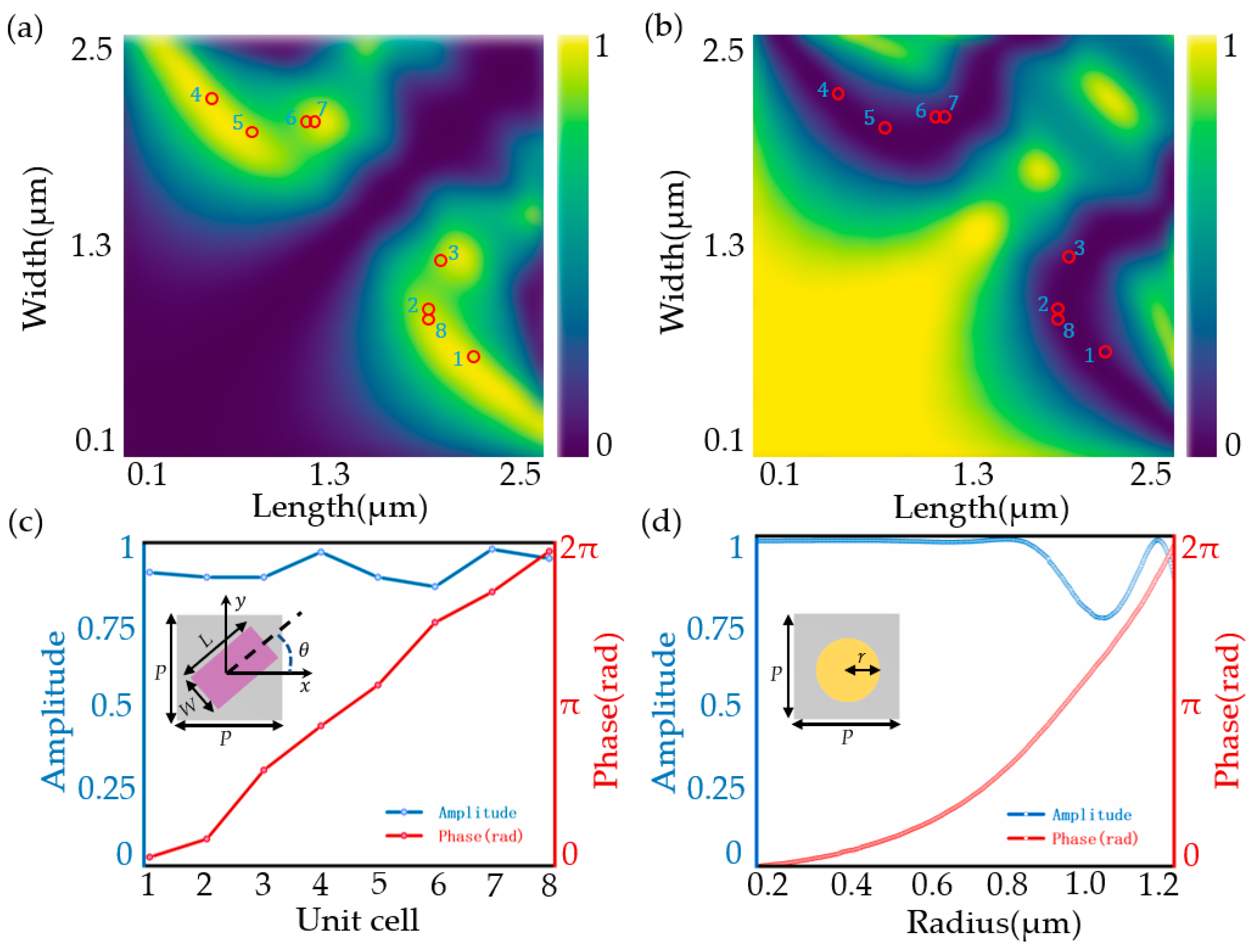
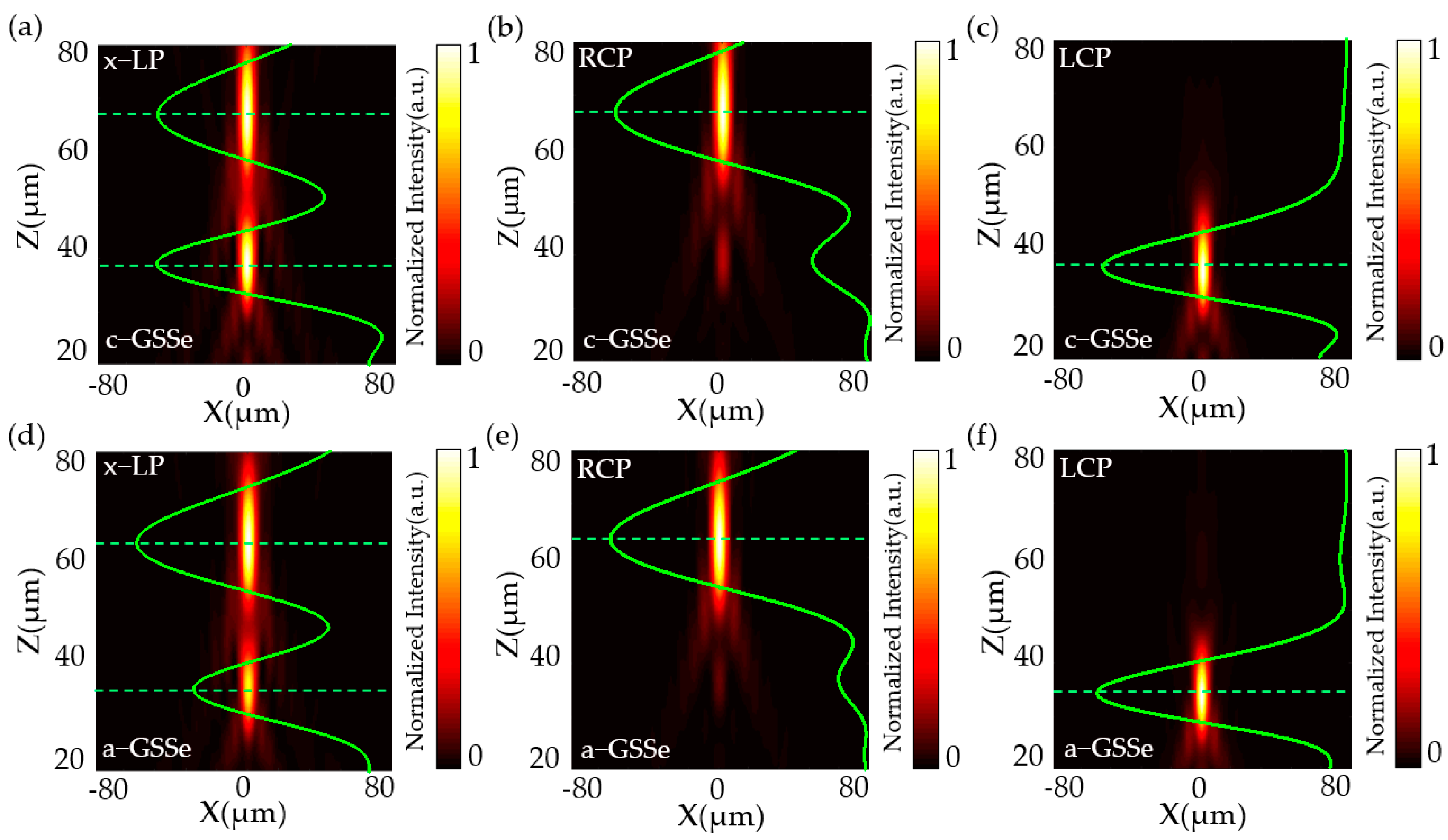
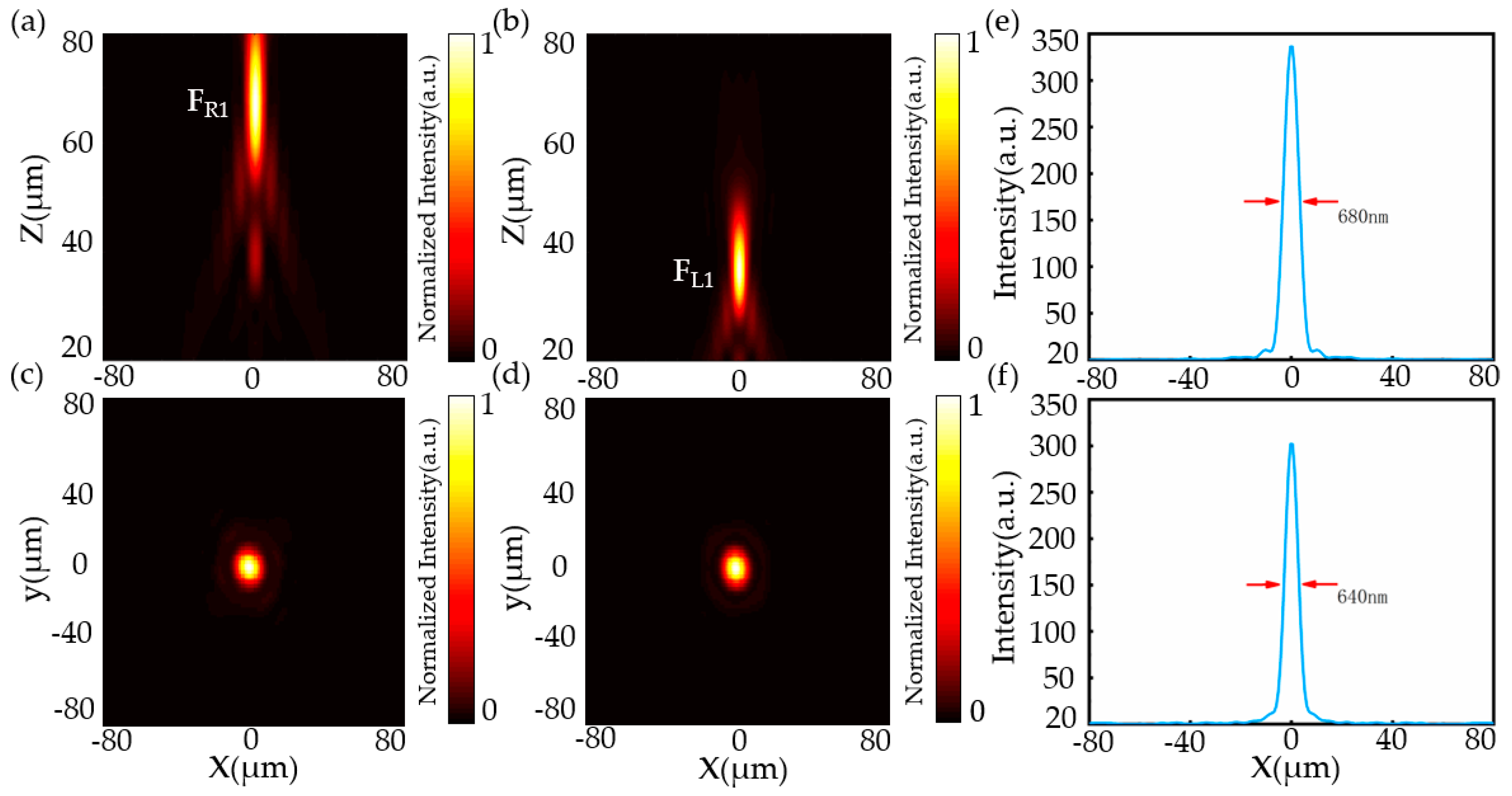
3.1. Polarization-Dependent Varifocal Metalens
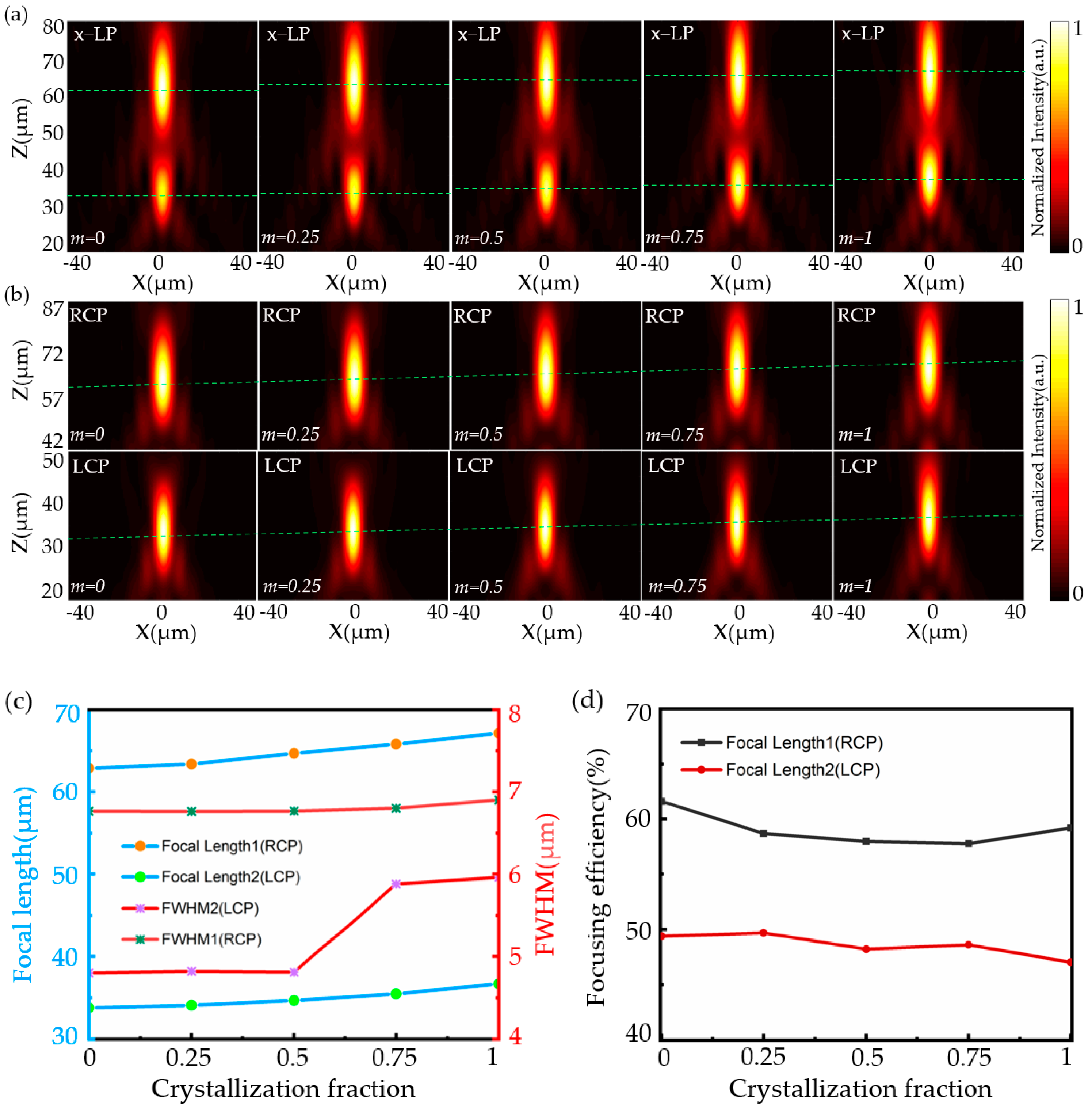
3.2. Polarization-Dependent Continuous Varifocal Metalens
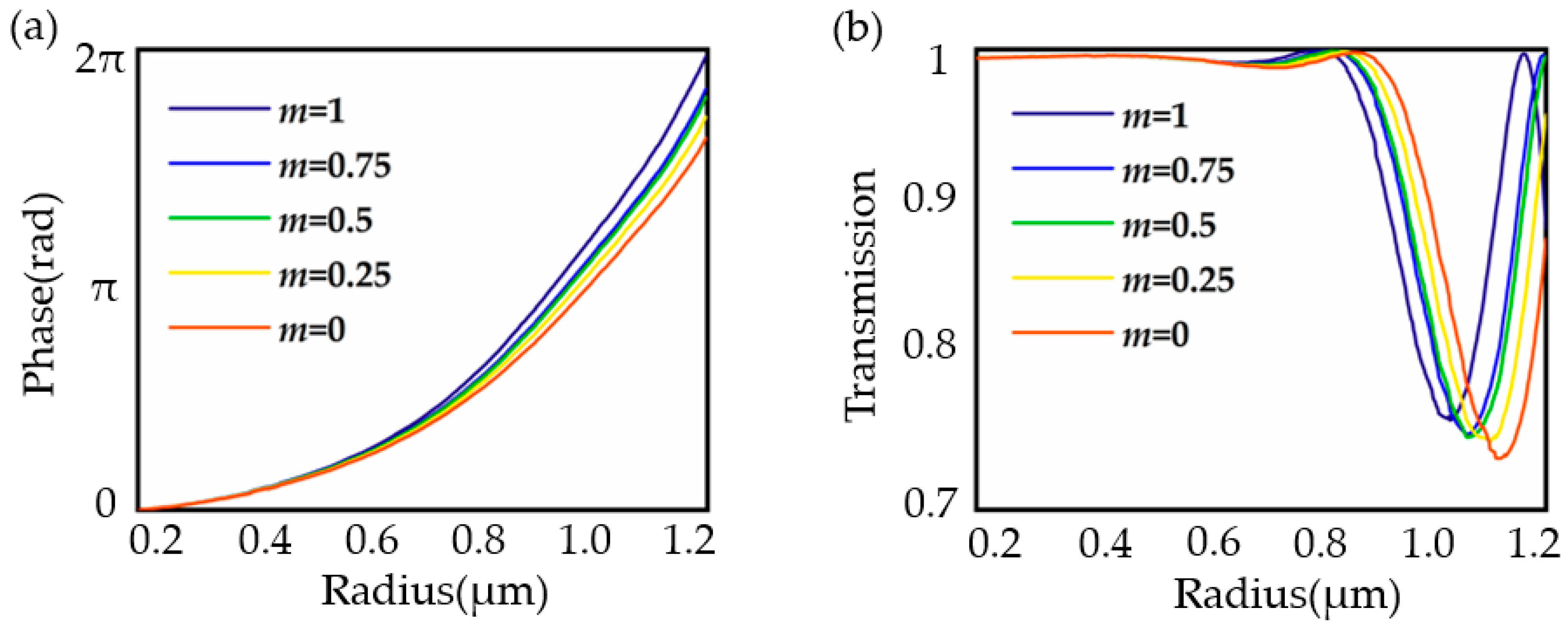
3.3. Bifocal Metalens with Adjustable Intensity Ratios
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Decker, M.; Staude, I.; Falkner, M.; Dominguez, J.; Neshev, D.N.; Brener, I.; Pertsch, T.; Kivshar, Y.S. High-Efficiency Dielectric Huygens’ Surfaces. Adv. Opt. Mater. 2015, 3, 813–820. [Google Scholar] [CrossRef] [Green Version]
- Ou, K.; Yu, F.; Li, G.; Wang, W.; Miroshnichenko, A.E.; Huang, L.J.; Wang, P.; Li, T.; Li, Z.; Chen, X.S.; et al. Mid-infrared polarization-controlled broadband achromatic metadevice. Sci. Adv. 2020, 6, eabc0711. [Google Scholar] [CrossRef] [PubMed]
- Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary spin-to–orbital angular momentum conversion of light. Science 2017, 358, 896–901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraon, A. Multiwavelength polarization-insensitive lenses based on dielectric metasurfaces with meta-molecules. Optica 2016, 3, 628–633. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Wu, P.C.; Su, V.C.; Lai, Y.C.; Chen, M.K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.T.; Wang, J.H.; et al. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef]
- Zhou, K.S.; Wang, B.X.; Tang, S.W.; Gao, Y.X.; Liu, S.; Sheng, Y.; Chen, J.J.; Dai, S.X.; Shen, X. Mid-infrared biomimetic moth-eye-shaped polarization-maintaining and angle-insensitive metalens. Opt. Express 2022, 30, 12048–12060. [Google Scholar] [CrossRef]
- Wang, Y.L.; Fan, Q.B.; Xu, T. Design of high efficiency achromatic metalens with large operation bandwidth using bilayer architecture. Opto-Electron. Adv. 2021, 4, 200008. [Google Scholar] [CrossRef]
- Zuo, H.J.; Choi, D.Y.; Gai, X.; Ma, P.; Xu, L.; Neshev, D.N.; Zhang, B.; Luther-Davies, B. High-Efficiency All-Dielectric Metalenses for Mid-Infrared Imaging. Adv. Opt. Mater. 2017, 5, 1700585. [Google Scholar] [CrossRef] [Green Version]
- Badloe, T.; Kim, I.; Kim, Y.; Kim, J.; Rho, J. Electrically Tunable Bifocal Metalens with Diffraction-Limited Focusing and Imaging at Visible Wavelengths. Adv. Sci. 2021, 8, 2102646. [Google Scholar] [CrossRef]
- Shan, D.; Xu, N.X.; Gao, J.S.; Song, N.T.; Liu, H.; Tang, Y.; Feng, X.G.; Wang, Y.S.; Zhao, Y.; Chen, X.; et al. Design of the all-silicon long-wavelength infrared achromatic metalens based on deep silicon etching. Opt. Express 2022, 30, 13616–13629. [Google Scholar] [CrossRef]
- Ding, F.; Chang, B.D.; Wei, Q.S.; Huang, L.L.; Guan, X.W.; Bozhevolnyi, S.I. Versatile Polarization Generation and Manipulation Using Dielectric Metasurfaces. Laser Photonics Rev. 2020, 14, 2000116. [Google Scholar] [CrossRef]
- Ren, H.; Fang, X.Y.; Jang, J.; Burger, J.; Rho, J.; Maier, S.A. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat. Nanotechnol. 2020, 15, 948–955. [Google Scholar] [CrossRef]
- Xu, J.; Li, R.Q.; Wang, S.Y.; Han, T.C. Ultra-broadband linear polarization converter based on anisotropic metasurface. Opt. Express 2018, 26, 26235–26241. [Google Scholar] [CrossRef]
- Yu, N.F.; Aieta, F.; Genevet, P.; Kats, M.A.; Gaburro, Z.; Capasso, F. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 2012, 12, 6328–6333. [Google Scholar] [CrossRef]
- Teng, S.; Zhang, Q.; Wang, H.; Liu, L.X.; Lv, H. Conversion between polarization states based on a metasurface. Photonics Res. 2019, 7, 246. [Google Scholar] [CrossRef] [Green Version]
- Genevet, P.; Yu, N.; Aieta, F.; Lin, J.; Kats, M.A.; Blanchard, R.; Scully, M.O.; Gaburro, Z.; Capasso, F. Ultra-thin plasmonic optical vortex plate based on phase discontinuities. Appl. Phys. Lett. 2012, 100, 013101. [Google Scholar] [CrossRef] [Green Version]
- Ou, K.; Li, G.H.; Li, T.X.; Yang, H.; Yu, F.L.; Chen, J.; Zhao, Z.Y.; Cao, G.G.; Chen, X.S.; Lu, W. High efficiency focusing vortex generation and detection with polarization-insensitive dielectric metasurfaces. Nanoscale 2018, 10, 19154–19161. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.; Guo, Z.Y.; Li, R.Z.; Zhang, J.R.; Zhang, A.J.; Qu, S.L. Ultra-thin optical vortex phase plate based on the metasurface and the angular momentum transformation. J. Opt. 2015, 17, 045102. [Google Scholar] [CrossRef]
- Ding, F.; Chen, Y.T.; Bozhevolnyi, S.I. Focused vortex-beam generation using gap-surface plasmon metasurfaces. Nanophotonics 2020, 9, 371–378. [Google Scholar] [CrossRef]
- He, J.W.; Ye, J.S.; Wang, X.K.; Kan, Q.; Zhang, Y. A broadband terahertz ultrathin multi-focus lens. Sci. Rep. 2016, 6, 28800. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.Z.; Chen, M.; Mehmood, M.Q.; Wen, D.; Yue, F.; Qiu, C.W.; Zhang, S. Longitudinal Multifoci Metalens for Circularly Polarized Light. Adv. Opt. Mater. 2015, 3, 1201–1206. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.Q.; Plum, E.; Xu, Q.; Wei, M.G.; Xu, Y.H.; Zhang, H.F.; Liao, Y.; Gu, J.Q.; Han, J.G.; et al. Polarization and Frequency Multiplexed Terahertz Meta-Holography. Adv. Opt. Mater. 2017, 5, 1700277. [Google Scholar] [CrossRef] [Green Version]
- Ji, R.; Chen, K.J.; Ni, Y.J.; Hua, Y.N.; Long, K.; Zhuang, S.L. Dual-Focuses Metalens for Copolarized and Cross-Polarized Transmission Waves. Adv. Cond. Matter Phys. 2018, 2018, 2312694. [Google Scholar] [CrossRef] [Green Version]
- Ee, H.S.; Agarwal, R. Tunable Metasurface and Flat Optical Zoom Lens on a Stretchable Substrate. Nano Lett. 2016, 16, 2818–2823. [Google Scholar] [CrossRef] [PubMed]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Horie, Y.; Faraon, A. Highly tunable elastic dielectric metasurface lenses. Laser Photonics Rev. 2016, 10, 1002–1008. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.B.; Cao, G.Y.; Lin, H.; Yuan, X.C.; Somekh, M.; Jia, B. A Varifocal Graphene Metalens for Broadband Zoom Imaging Covering the Entire Visible Region. ACS Nano 2021, 15, 4769–4776. [Google Scholar] [CrossRef]
- Cui, Y.; Zheng, G.X.; Chen, M.; Zhang, Y.L.; Yang, Y.; Tao, J.; He, T.T.; Li, Z.L. Reconfigurable continuous-zoom metalens in visible band. Chin. Opt. Lett. 2019, 17, 111603. [Google Scholar] [CrossRef]
- Iwami, K.; Ogawa, C.; Nagase, T.; Ikezawa, S. Demonstration of focal length tuning by rotational varifocal moire metalens in an ir-A wavelength. Opt. Express 2020, 28, 35602–35614. [Google Scholar] [CrossRef]
- Wang, C.; Sun, Y.; Zhang, Q.B.; Yu, Z.Q.; Tao, C.N.; Zhang, J.L.; Wu, F.; Wu, R.; Zheng, Z. Continuous-zoom bifocal metalens by mutual motion of cascaded bilayer metasurfaces in the visible. Opt. Express 2021, 29, 26569–26585. [Google Scholar] [CrossRef]
- Colburn, S.; Zhan, A.; Majumdar, A. Varifocal zoom imaging with large area focal length adjustable metalenses. Optica 2018, 5, 825. [Google Scholar] [CrossRef]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraji-Dana, M.S.; Faraon, A. MEMS-tunable dielectric metasurface lens. Nat. Commun. 2018, 9, 812. [Google Scholar] [CrossRef] [Green Version]
- Han, Z.Y.; Colburn, S.; Majumdar, A.; Bohringer, K.F. MEMS-actuated metasurface Alvarez lens. Microsyst. Nanoeng. 2020, 6, 79. [Google Scholar] [CrossRef]
- Meng, C.; Thrane, P.C.V.; Ding, F.; Gjessing, J.; Thomaschewski, M.; Wu, C.; Dirdal, C.; Bozhevolnyi, S.I. Dynamic piezoelectric MEMS-based optical metasurfaces. Sci. Adv. 2021, 7, 5639. [Google Scholar] [CrossRef]
- Zhou, S.H.; Shen, Z.X.; Li, X.N.; Ge, S.J.; Lu, Y.Q.; Hu, W. Liquid crystal integrated metalens with dynamic focusing property. Opt. Lett. 2020, 45, 4324–4327. [Google Scholar] [CrossRef]
- Bosch, M.; Shcherbakov, M.R.; Won, K.; Lee, H.S.; Kim, Y.; Shvets, G. Electrically Actuated Varifocal Lens Based on Liquid-Crystal-Embedded Dielectric Metasurfaces. Nano Lett. 2021, 21, 3849–3856. [Google Scholar] [CrossRef]
- Shen, Z.X.; Zhou, S.H.; Li, X.N.; Ge, S.J.; Chen, P.; Hu, W.; Lu, Y.Q. Liquid crystal integrated metalens with tunable chromatic aberration. Adv. Photonics 2020, 2, 036002. [Google Scholar] [CrossRef]
- Ding, P.; Li, Y.; Shao, L.; Tian, X.M.; Wang, J.Q.; Fan, C.Z. Graphene aperture-based metalens for dynamic focusing of terahertz waves. Opt. Express 2018, 26, 28038–28050. [Google Scholar] [CrossRef]
- He, J.J.; Chen, R.K.; Li, Y.F.; Chen, S.P.; Liu, Z.M.; Zhang, Q.M. Graphene metalens with dynamic focusing and plane focusing in the terahertz range. Appl. Opt. 2021, 60, 5752–5758. [Google Scholar] [CrossRef]
- Zhang, Z.K.; Qi, X.Q.; Zhang, J.F.; Guo, C.C.; Zhu, Z.H. Graphene-enabled electrically tunability of metalens in the terahertz range. Opt. Express 2020, 28, 28101–28112. [Google Scholar] [CrossRef]
- Li, S.Y.; Zhou, C.B.; Ban, G.X.; Wang, H.; Lu, H.; Wang, Y. Active all-dielectric bifocal metalens assisted by germanium antimony telluride. J. Phys. D 2019, 52, 095106. [Google Scholar] [CrossRef]
- Qin, S.; Xu, N.; Huang, H.; Jie, K.Q.; Liu, H.Z.; Guo, J.P.; Meng, H.Y.; Wang, F.Q.; Yang, X.B.; Wei, Z.C. Near-infrared thermally modulated varifocal metalens based on the phase change material Sb2S3. Opt. Express 2021, 29, 7925–7934. [Google Scholar] [CrossRef] [PubMed]
- Shalaginov, M.Y.; An, S.; Zhang, Y.F.; Yang, F.; Su, P.; Liberman, V.; Chou, J.B.; Roberts, C.M.; Kang, M.; Rios, C.; et al. Reconfigurable all-dielectric metalens with diffraction-limited performance. Nat. Commun. 2021, 12, 1225. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Q.; Chen, L.; Tang, S.W.; Xu, P.P.; Ding, F.; Fang, Z.R.; Majumdar, A. Helicity-dependent continuous varifocal metalens based on bilayer dielectric metasurfaces. Opt. Express 2021, 29, 39461–39472. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.H.; Steinle, T.; Huang, L.L.; Taubner, T.; Wuttig, M.; Zentgraf, T.; Giessen, H. Beam switching and bifocal zoom lensing using active plasmonic metasurfaces. Light Sci. Appl. 2017, 6, 17016. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Chou, J.B.; Li, J.Y.; Li, H.S.; Du, Q.Y.; Yadav, A.; Zhou, S.; Shalaginov, M.Y.; Fang, Z.R.; Zhong, H.K.; et al. Broadband transparent optical phase change materials for high-performance nonvolatile photonics. Nat. Commun. 2019, 10, 4279. [Google Scholar]
- Zhang, Y.F.; Li, J.Y.; Chou, J.B.; Fang, Z.R.; Yadav, A.; Lin, H.; Du, Q.; Michon, J.; Han, Z.H.; Huang, Y.Z.; et al. Broadband Transparent Optical Phase Change Materials; Optica Publishing Group: San Jose, CA, USA, 2017; p. JTh5C-4. [Google Scholar]
- Lin, R.G.; Li, X.H. Multifocal metalens based on multilayer Pancharatnam–Berry phase elements architecture. Opt. Lett. 2019, 44, 2819–2822. [Google Scholar]
- Chen, L.; Hao, Y.; Zhao, L.; Wu, R.; Liu, Y.; Wei, Z.C.; Xu, N.; Li, Z.T.; Liu, H.Z. Multifunctional metalens generation using bilayer all-dielectric metasurfaces. Opt. Express 2021, 29, 9332–9345. [Google Scholar] [CrossRef]
- Tian, S.N.; Guo, H.M.; Hu, J.B.; Zhuang, S.L. Dielectric longitudinal bifocal metalens with adjustable intensity and high focusing efficiency. Opt. Express 2019, 27, 680–688. [Google Scholar] [CrossRef]
- Zhou, Y.; Kravchenko, I.I.; Wang, H.; Nolen, J.R.; Gu, G.; Valentine, J. Multilayer Noninteracting Dielectric Metasurfaces for Multiwavelength Metaoptics. Nano Lett. 2018, 18, 7529–7537. [Google Scholar]
- Liu, M.Z.; Huo, P.C.; Zhu, W.Q.; Zhang, C.; Zhang, S.; Song, M.W.; Zhang, S.; Zhou, Q.W.; Chen, L.; Lezec, H.J.; et al. Broadband generation of perfect Poincare beams via dielectric spin-multiplexed metasurface. Nat. Commun. 2021, 12, 2230. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Ren, Z.R.; Shu, Y.C.; Wu, L.J.; Sun, J.H.; Cai, H.; Zhang, X.T.; Lu, L.; Qi, K.N.; Li, L.S.; et al. Broadband, large-numerical-aperture and high-efficiency microwave metalens by using a double-layer transmissive metasurface. Appl. Phys. Express 2022, 15, 014003. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Sun, J.H.; Shu, Y.C.; Wu, L.J.; Lu, L.; Qi, K.N.; Che, Y.X.; Li, L.S.; Yin, H.C. High numerical aperture and large focusing efficiency metalens based on multilayer transmitarray elements. Opt. Lasers Eng. 2021, 147, 106734. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, L.; Zhou, K.; Zhao, F.; Gao, Y.; Wang, B.; Shen, X. Mid-Infrared Continuous Varifocal Metalens with Adjustable Intensity Based on Phase Change Materials. Photonics 2022, 9, 959. https://doi.org/10.3390/photonics9120959
Shao L, Zhou K, Zhao F, Gao Y, Wang B, Shen X. Mid-Infrared Continuous Varifocal Metalens with Adjustable Intensity Based on Phase Change Materials. Photonics. 2022; 9(12):959. https://doi.org/10.3390/photonics9120959
Chicago/Turabian StyleShao, Liangde, Kongsi Zhou, Fangfang Zhao, Yixiao Gao, Bingxia Wang, and Xiang Shen. 2022. "Mid-Infrared Continuous Varifocal Metalens with Adjustable Intensity Based on Phase Change Materials" Photonics 9, no. 12: 959. https://doi.org/10.3390/photonics9120959
APA StyleShao, L., Zhou, K., Zhao, F., Gao, Y., Wang, B., & Shen, X. (2022). Mid-Infrared Continuous Varifocal Metalens with Adjustable Intensity Based on Phase Change Materials. Photonics, 9(12), 959. https://doi.org/10.3390/photonics9120959



