Transversal Kerr Effect Enhancement of Permalloy-Based Shallow Lamellar Magnetoplasmonic Crystals
Abstract
:1. Introduction
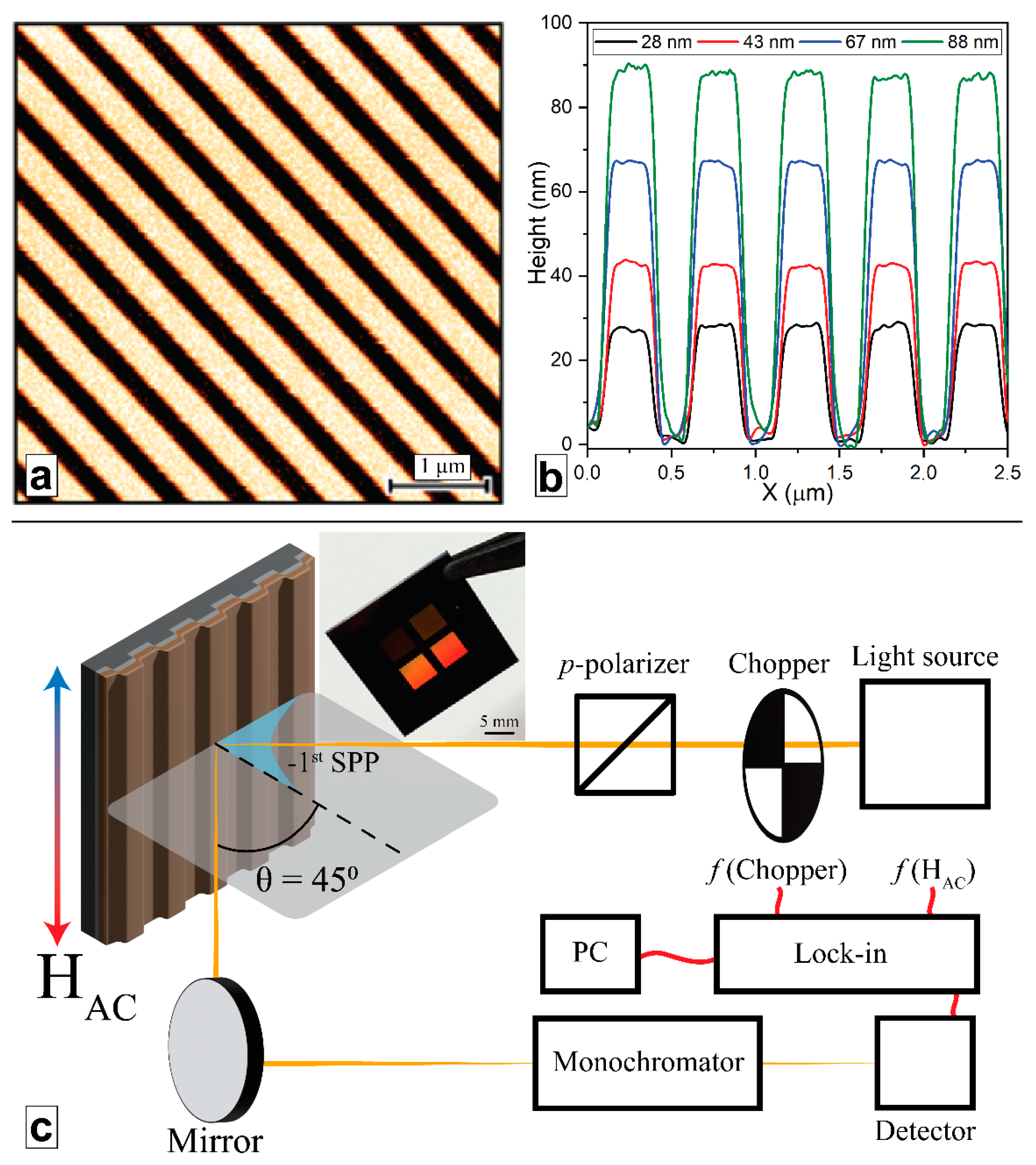
2. Materials and Methods
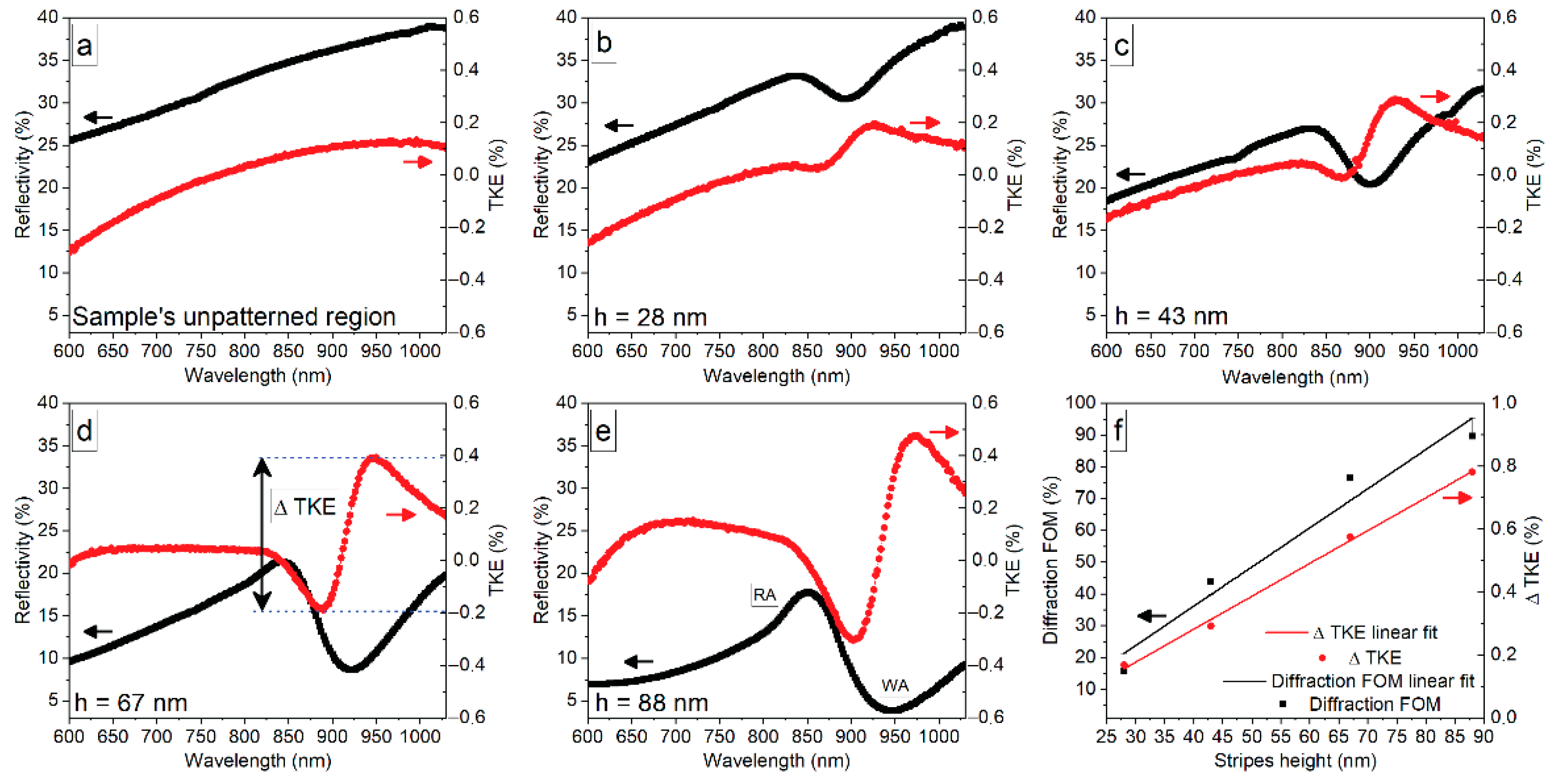
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic Surface Lattice Resonances: A Review of Properties and Applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef] [PubMed]
- Jiang, N.; Zhuo, X.; Wang, J. Active Plasmonics: Principles, Structures, and Applications. Chem. Rev. 2018, 118, 3054–3099. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Peng, Y.; Yang, Y.; Li, Z.-Y. Plasmon-Enhanced Light–Matter Interactions and Applications. npj Comput. Mater. 2019, 5, 45. [Google Scholar] [CrossRef] [Green Version]
- Chou, K.-H.; Lin, E.-P.; Chen, T.-C.; Lai, C.-H.; Wang, L.-W.; Chang, K.-W.; Lee, G.-B.; Lee, M.-C.M. Application of Strong Transverse Magneto-Optical Kerr Effect on High Sensitive Surface Plasmon Grating Sensors. Opt. Express 2014, 22, 19794. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.; Zhai, X.; Wang, L.; Xiang, Y.; Wen, S. Plasmonically Induced Transparency in Phase-Coupled Graphene Nanoribbons. Phys. Rev. B 2022, 106, 075401. [Google Scholar] [CrossRef]
- Guan, J.; Xia, S.; Zhang, Z.; Wu, J.; Meng, H.; Yue, J.; Zhai, X.; Wang, L.; Wen, S. Two Switchable Plasmonically Induced Transparency Effects in a System with Distinct Graphene Resonators. Nanoscale Res. Lett. 2020, 15, 142. [Google Scholar] [CrossRef]
- Musorin, A.I.; Chetvertukhin, A.V.; Dolgova, T.V.; Uchida, H.; Inoue, M.; Luk’yanchuk, B.S.; Fedyanin, A.A. Tunable Multimodal Magnetoplasmonic Metasurfaces. Appl. Phys. Lett. 2019, 115, 151102. [Google Scholar] [CrossRef]
- Armelles, G.; Cebollada, A.; García-Martín, A.; González, M.U. Magnetoplasmonics: Combining Magnetic and Plasmonic Functionalities. Adv. Opt. Mater. 2013, 1, 10–35. [Google Scholar] [CrossRef] [Green Version]
- Borovkova, O.V.; Hashim, H.; Ignatyeva, D.O.; Kozhaev, M.A.; Kalish, A.N.; Dagesyan, S.A.; Shaposhnikov, A.N.; Berzhansky, V.N.; Achanta, V.G.; Panina, L.V.; et al. Magnetoplasmonic Structures with Broken Spatial Symmetry for Light Control at Normal Incidence. Phys. Rev. B 2020, 102, 081405. [Google Scholar] [CrossRef]
- Belotelov, V.; Akimov, I.; Pohl, M.; Kotov, V.A.; Kasture, S.; Vengurlekar, A.S.; Gopal, A.V.; Yakovlev, D.R.; Zvezdin, A.K.; Bayer, M. Enhanced magneto-optical effects in magnetoplasmonic crystals. Nat. Nanotech 2011, 6, 370–376. [Google Scholar] [CrossRef]
- Belyaev, V.K.; Murzin, D.V.; Perova, N.N.; Grunin, A.A.; Fedyanin, A.A.; Rodionova, V.V. Permalloy-Based Magnetoplasmonic Crystals for Sensor Applications. J. Magn. Magn. Mater. 2019, 482, 292–295. [Google Scholar] [CrossRef]
- Grunin, A.A.; Mukha, I.R.; Chetvertukhin, A.V.; Fedyanin, A.A. Refractive Index Sensor Based on Magnetoplasmonic Crystals. J. Magn. Magn. Mater. 2016, 415, 72–76. [Google Scholar] [CrossRef]
- Belyaev, V.K.; Rodionova, V.V.; Grunin, A.A.; Inoue, M.; Fedyanin, A.A. Magnetic Field Sensor Based on Magnetoplasmonic Crystal. Sci. Rep. 2020, 10, 7133. [Google Scholar] [CrossRef] [PubMed]
- de la Cruz, S.; Méndez, E.R.; Macías, D.; Salas-Montiel, R.; Adam, P.M. Compact Surface Structures for the Efficient Excitation of Surface Plasmon-Polaritons. Phys. Status Solidi Basic Res. 2012, 249, 1178–1187. [Google Scholar] [CrossRef]
- Smith, C.L.C.; Stenger, N.; Kristensen, A.; Mortensen, N.A.; Bozhevolnyi, S.I. Gap and Channeled Plasmons in Tapered Grooves: A Review. Nanoscale 2015, 7, 9355–9386. [Google Scholar] [CrossRef] [Green Version]
- Kiryanov, M.A.; Frolov, A.Y.; Novikov, I.A.; Kipp, P.A.; Nurgalieva, P.K.; Popov, V.V.; Ezhov, A.A.; Dolgova, T.V.; Fedyanin, A.A. Surface Profile-Tailored Magneto-Optics in Magnetoplasmonic Crystals. APL Photonics 2022, 7, 026104. [Google Scholar] [CrossRef]
- Popov, E.; Tsonev, L.; Maystre, D. Lamellar Metallic Grating Anomalies. Appl. Opt. 1994, 33, 5214. [Google Scholar] [CrossRef]
- Popov, E.K.; Bonod, N.; Enoch, S. Comparison of Plasmon Surface Waves on Shallow and Deep Metallic 1D and 2D Gratings. Opt. Express 2007, 15, 4224. [Google Scholar] [CrossRef]
- Bonod, N.; Tayeb, G.; Maystre, D.; Enoch, S.; Popov, E. Total Absorption of Light by Lamellar Metallic Gratings. Opt. Express 2008, 16, 15431. [Google Scholar] [CrossRef] [Green Version]
- Le Perchec, J.; Quémerais, P.; Barbara, A.; López-Ríos, T. Why Metallic Surfaces with Grooves a Few Nanometers Deep and Wide May Strongly Absorb Visible Light. Phys. Rev. Lett. 2008, 100, 066408. [Google Scholar] [CrossRef]
- Ávalos, L.; González-Alcalde, A.K.; Chaikina, E.I.; García-Guerrero, E.E.; Maradudin, A.A.; Méndez, E.R. Excitation of Plasmonic and Photonic Modes in Metallic Lamellar Gratings. Opt. Commun. 2021, 500, 127324. [Google Scholar] [CrossRef]
- K-Layout. Available online: https://www.klayout.de/ (accessed on 1 December 2022).
- Hubert, A.; Schäfer, R. Magnetic Domains: The Analysis of Magnetic Microstructures; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Maradudin, A.A.; Simonsen, I.; Polanco, J.; Fitzgerald, R.M. Rayleigh and Wood Anomalies in the Diffraction of Light from a Perfectly Conducting Reflection Grating. J. Opt. 2016, 18, 024004. [Google Scholar] [CrossRef] [Green Version]
- Halagačka, L.; Vanwolleghem, M.; Postava, K.; Dagens, B.; Pištora, J. Coupled Mode Enhanced Giant Magnetoplasmonics Transverse Kerr Effect. Opt. Express 2013, 21, 21741. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tikuišis, K.K.; Beran, L.; Cejpek, P.; Uhlířová, K.; Hamrle, J.; Vaňatka, M.; Urbánek, M.; Veis, M. Optical and Magneto-Optical Properties of Permalloy Thin Films in 0.7–6.4 EV Photon Energy Range. Mater. Des. 2017, 114, 31–39. [Google Scholar] [CrossRef]
- Cowan, J.J.; Arakawa, E.T. Dispersion of Surface Plasmons in Dielectric-Metal Coatings on Concave Diffraction Gratings. Zeitschrift Phys. 1970, 235, 97–109. [Google Scholar] [CrossRef]
- Kleemann, B.; Guther, R. Metal Gratings with Dielectric Coating of Variable Thickness within a Period. J. Mod. Opt. 1991, 38, 897–910. [Google Scholar] [CrossRef]
- Maystre, D. Theory of Wood’s Anomalies. In Plasmonics: From Basics to Advanced Topics; Enoch, S., Bonod, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 39–83. ISBN 978-3-642-28079-5. [Google Scholar]
- Darweesh, A.A.; Bauman, S.J.; Debu, D.T.; Herzog, J.B. The Role of Rayleigh-Wood Anomalies and Surface Plasmons in Optical Enhancement for Nano-Gratings. Nanomaterials 2018, 8, 809. [Google Scholar] [CrossRef] [Green Version]
- Savoia, S.; Ricciardi, A.; Crescitelli, A.; Granata, C.; Esposito, E.; Galdi, V.; Cusano, A. Surface Sensitivity of Rayleigh Anomalies in Metallic Nanogratings. Opt. Express 2013, 21, 23531. [Google Scholar] [CrossRef] [Green Version]
- Belotelov, V.I.; Bykov, D.A.; Doskolovich, L.L.; Kalish, A.N.; Zvezdin, A.K. Giant Transversal Kerr Effect in Magneto-Plasmonic Heterostructures: The Scattering-Matrix Method. J. Exp. Theor. Phys. 2010, 110, 816–824. [Google Scholar] [CrossRef]
- Feigenbaum, E.; Orenstein, M. Modeling of Complementary (Void) Plasmon Waveguiding. J. Light. Technol. 2007, 25, 2547–2562. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murzin, D.; Belyaev, V.; Kern, J.; Kaspar, C.; Pernice, W.H.; Bratschitsch, R.; Rodionova, V. Transversal Kerr Effect Enhancement of Permalloy-Based Shallow Lamellar Magnetoplasmonic Crystals. Photonics 2022, 9, 989. https://doi.org/10.3390/photonics9120989
Murzin D, Belyaev V, Kern J, Kaspar C, Pernice WH, Bratschitsch R, Rodionova V. Transversal Kerr Effect Enhancement of Permalloy-Based Shallow Lamellar Magnetoplasmonic Crystals. Photonics. 2022; 9(12):989. https://doi.org/10.3390/photonics9120989
Chicago/Turabian StyleMurzin, Dmitry, Victor Belyaev, Johannes Kern, Corinna Kaspar, Wolfram H. Pernice, Rudolf Bratschitsch, and Valeria Rodionova. 2022. "Transversal Kerr Effect Enhancement of Permalloy-Based Shallow Lamellar Magnetoplasmonic Crystals" Photonics 9, no. 12: 989. https://doi.org/10.3390/photonics9120989
APA StyleMurzin, D., Belyaev, V., Kern, J., Kaspar, C., Pernice, W. H., Bratschitsch, R., & Rodionova, V. (2022). Transversal Kerr Effect Enhancement of Permalloy-Based Shallow Lamellar Magnetoplasmonic Crystals. Photonics, 9(12), 989. https://doi.org/10.3390/photonics9120989





