Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach
Abstract
:1. Introduction
2. Experimental Section
3. Theory
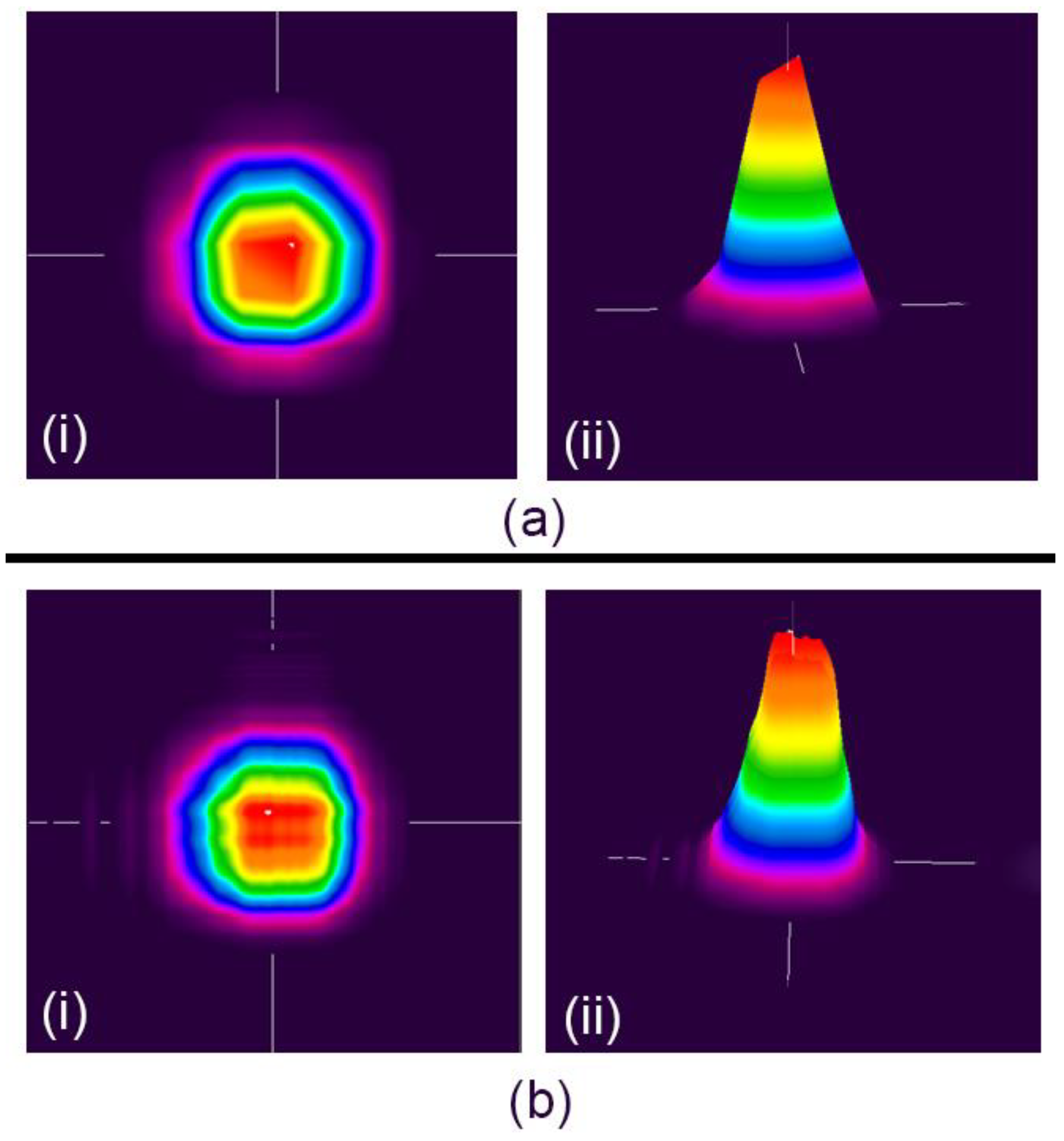
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Fourmaux, S.; Payeur, S.; Alexandrov, A.; Serbanescu, C.; Martin, F.; Ozaki, T.; Kudryashov, A.; Kieffer, J.C. Laser Beam Wavefront Correction for Ultra High Intensities with the 200 TW Laser System at the Advanced Laser Light Source. Opt. Express 2008, 16, 11987. [Google Scholar] [CrossRef] [PubMed]
- Samelsohn, G.; Mazar, R. Adaptive Wavefront Tilt Correction for Imaging and Laser Beam Formation in a Turbulent Atmosphere. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium, IGARSS ’95. Quantitative Remote Sensing for Science and Applications, Firenze, Italy, 10–14 July 1995; Volume 3, pp. 1941–1943. [Google Scholar]
- Huot, N.; Jonathan, J.-M.C.; Roosen, G. Dynamic Wavefront Correction of Nd:YAG Lasers by Self-Pumped Phase Conjugation in Photorefractive BaTiO/Sub 3/:Rh. Proc. IEEE 1999, 87, 2059–2073. [Google Scholar] [CrossRef]
- Salter, P.S.; Booth, M.J. Adaptive Optics in Laser Processing. Light Sci. Appl. 2019, 8, 110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Y.; Zhong, L.; Min, L.; Wang, J.; Wu, Y.; Chen, K.; Wei, K.; Rao, C. Adaptive Optics Based on Machine Learning: A Review. Opto-Electron. Adv. 2022, 5, 200082. [Google Scholar] [CrossRef]
- Rukosuev, A.L.; Kudryashov, A.V.; Lylova, A.N.; Samarkin, V.V.; Sheldakova, Y.V. Adaptive Optics System for Real-Time Wavefront Correction. Atmos. Ocean. Opt. 2015, 28, 381–386. [Google Scholar] [CrossRef]
- Ribak, E. Atmospheric Turbulence, Speckle, and Adaptive Optics. Ann. N. Y. Acad. Sci. 1997, 808, 193–204. [Google Scholar] [CrossRef]
- Qin, Z.; She, Z.; Chen, C.; Wu, W.; Lau, J.K.Y.; Ip, N.Y.; Qu, J.Y. Deep Tissue Multi-Photon Imaging Using Adaptive Optics with Direct Focus Sensing and Shaping. Nat. Biotechnol. 2022, 40, 1663–1671. [Google Scholar] [CrossRef]
- Hampson, K.M.; Turcotte, R.; Miller, D.T.; Kurokawa, K.; Males, J.R.; Ji, N.; Booth, M.J. Adaptive Optics for High-Resolution Imaging. Nat. Rev. Methods Prim. 2021, 1, 68. [Google Scholar] [CrossRef]
- Shealy, D.L. Historical Perspective of Laser Beam Shaping. In Proceedings of the Laser Beam Shaping III, Seattle, WA, USA, 28 October 2002; Volume 4770, pp. 28–47. [Google Scholar]
- Paschotta, R. Field Guide to Lasers; SPIE press: Bellingham, WA, USA, 2008; Volume 12, p. 9610. ISBN 081946. [Google Scholar]
- Mielec, N.; Altorio, M.; Sapam, R.; Horville, D.; Holleville, D.; Sidorenkov, L.A.; Landragin, A.; Geiger, R. Atom Interferometry with Top-Hat Laser Beams. Appl. Phys. Lett. 2018, 113, 161108. [Google Scholar] [CrossRef]
- Hou, Z.; Afgan, M.S.; Sheta, S.; Liu, J.; Wang, Z. Plasma Modulation Using Beam Shaping to Improve Signal Quality for Laser Induced Breakdown Spectroscopy. J. Anal. At. Spectrom. 2020, 35, 1671–1677. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Z.-J.; Pang, Z.-G.; Ge, Y.-R. The Complex-Valued Astigmatic Cosine-Gaussian Soliton Solution of the Nonlocal Nonlinear Schrödinger Equation and Its Transmission Characteristics. Appl. Math. Lett. 2022, 125, 107755. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Z.; Li, X.; Zhang, S. Periodic Propagation of Complex-Valued Hyperbolic-Cosine-Gaussian Solitons and Breathers with Complicated Light Field Structure in Strongly Nonlocal Nonlinear Media. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 106005. [Google Scholar] [CrossRef]
- Li, B.; Blaschke, H.; Ristau, D. Pulsed Photothermal Deflection with a Top-Hat Beam Excitation. J. Appl. Phys. 2006, 100, 053509. [Google Scholar] [CrossRef]
- Astrath, F.B.; Astrath, N.G.; Shen, J.; Zhou, J.; Malacarne, L.C.; Pedreira, P.R.B.; Baesso, M.L. Time-Resolved Thermal Mirror Technique with Top-Hat Cw Laser Excitation. Opt. Express 2008, 16, 12214. [Google Scholar] [CrossRef] [PubMed]
- Astrath, N.G.C.; Astrath, F.B.G.; Shen, J.; Zhou, J.; Gu, C.E.; Malacarne, L.C.; Pedreira, P.R.B.; Bento, A.C.; Baesso, M.L. Top-Hat Cw Laser Induced Thermal Mirror: A Complete Model for Material Characterization. Appl. Phys. B 2009, 94, 473–481. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Li, B.; Hao, H. Comparison of Signals under Top-Hat and Gaussian Beam Excitations in Surface Thermal Lens Technique. In Proceedings of the Optical Design and Testing III, Beijing, China, 28 November 2007; p. 68342D. [Google Scholar]
- Li, B.; Xiong, S.; Zhang, Y. Fresnel Diffraction Model for Mode-Mismatched Thermal Lens with Top-Hat Beam Excitation. Appl. Phys. B 2005, 80, 527–534. [Google Scholar] [CrossRef]
- Pawlak, M.; Kruck, T.; Spitzer, N.; Dziczek, D.; Ludwig, A.; Wieck, A.D. Experimental Validation of Formula for Calculation Thermal Diffusivity in Superlattices Performed Using a Combination of Two Frequency-Domain Methods: Photothermal Infrared Radiometry and Thermoreflectance. Appl. Sci. 2021, 11, 6125. [Google Scholar] [CrossRef]
- Boccara, A.C.; Jackson, W.; Amer, N.M.; Fournier, D. Sensitive Photothermal Deflection Technique for Measuring Absorption in Optically Thin Media. Opt. Lett. 1980, 5, 377. [Google Scholar] [CrossRef]
- Yun, S.I.; Seo, H.J. Photothermal Beam Deflection Technique for the Study of Solids? Chin. J. Phys. 1992, 30, 753–767. [Google Scholar]
- Cabrera, H.; Korte, D.; Budasheva, H.; Asbaghi, B.A.N.; Bellucci, S. Through-Plane and in-Plane Thermal Diffusivity Determination of Graphene Nanoplatelets by Photothermal Beam Deflection Spectrometry. Materials 2021, 14, 7273. [Google Scholar] [CrossRef]
- Vodišek, N.; Šuligoj, A.; Korte, D.; Štangar, U.L. Transparent Photocatalytic Thin Films on Flexible Polymer Substrates. Materials 2018, 11, 1945. [Google Scholar] [CrossRef] [PubMed]
- Soumya, S.; Arun Kumar, R.; Raj, V.; Swapna, M.S.; Sankararaman, S. Thermal Diffusivity of Molybdenum Oxide Nanowire Film: A Photothermal Beam Deflection Study. Opt. Laser Technol. 2021, 139, 106993. [Google Scholar] [CrossRef]
- Sell, J. Photothermal Investigations of Solids and Fluids, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 0323154220. [Google Scholar]
- Korte, D.; Franko, M. Photothermal Deflection Experiments: Comparison of Existing Theoretical Models and Their Applications to Characterization of TiO2-Based Thin Films. Int. J. Thermophys. 2014, 35, 2352–2362. [Google Scholar] [CrossRef]
- Soumya, S.; Raj, V.; Swapna, M.S.; Sankararaman, S. Thermal Diffusivity Downscaling of Molybdenum Oxide Thin Film through Annealing Temperature-Induced Nano-Lamelle Formation: A Photothermal Beam Deflection Study. Eur. Phys. J. Plus 2021, 136, 187. [Google Scholar] [CrossRef]
- Budasheva, H.; Kravos, A.; Korte, D.; Bratkič, A.; Gao, Y.; Franko, M. Determination of Dissolved Iron Redox Species in Freshwater Sediment Using DGT Technique Coupled to BDS. Acta Chim. Slov. 2019, 66, 239–246. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Korte, D.; Rogova, O.B.; Volkov, D.S.; Franko, M. Photothermal Beam Deflection Spectroscopy for the Determination of Thermal Diffusivity of Soils and Soil Aggregates. Int. J. Thermophys. 2018, 39, 81. [Google Scholar] [CrossRef]
- Li, B.; Welsch, E. Probe-Beam Diffraction in a Pulsed Top-Hat Beam Thermal Lens with a Mode-Mismatched Configuration. Appl. Opt. 1999, 38, 5241. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Chen, X.; Gong, Y. Analysis of Surface Thermal Lens Signal in Optical Coatings with Top-Hat Beam Excitation. J. Appl. Phys. 2008, 103, 033518. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Powell, R.W.; Ho, C.Y.; Klemens, P.G. Thermophysical Properties of Matter-the TPRC Data Series. In Thermal Conductivity-Metallic Elements and Alloys (Reannouncement); Data Book; Purdue University, Thermophysical and Electronic Properties Information Center: Lafayette, IN, USA, 1970; Volume 1. [Google Scholar]
- Omini, M.; Sparavigna, A.; Strigazzi, A. Dilatometric Determination of Thermal Diffusivity in Low Conducting Materials. Meas. Sci. Technol. 1990, 1, 166–171. [Google Scholar] [CrossRef]
- Instruments, T.T. Materials Thermal Properties Database. Available online: https://thermtest.com/thermal-resources/materials-database (accessed on 25 November 2022).
- Aamodt, L.C.; Murphy, J.C. Photothermal Measurements Using a Localized Excitation Source. J. Appl. Phys. 1981, 52, 4903–4914. [Google Scholar] [CrossRef]
- Aamodt, L.C.; Murphy, J.C. Thermal Effects in Photothermal Spectroscopy and Photothermal Imaging. J. Appl. Phys. 1983, 54, 581–591. [Google Scholar] [CrossRef]
- Glazov, A.L.; Muratikov, K.L. Calculation of the Photodeflection Signal in the Framework of Wave Optics. Technol. Phys. 1993, 38, 344–347. [Google Scholar]
- Glazov, A.L.; Muratikov, K.L. Photodeflection and Interferometric Thermal Wave Microscopy of Solids. Int. J. Optoelectron. 1989, 4, 589–597. [Google Scholar]
- Kobylinska, D.K.; Bukowski, R.J.; Burak, B.; Bodzenta, J.; Kochowski, S. The Complex Ray Theory of Photodeflection Signal Formation: Comparison with the Ray Theory and the Experimental Results. J. Appl. Phys. 2006, 100, 063501. [Google Scholar] [CrossRef]
- Bukowski, R.J.; Korte, D. Perturbation Calculus for Eikonal Application to Analysis of the Deflectional Signal in Photothermal Measurements. Opt. Appl. 2002, 32, 817–828. [Google Scholar]
- Kobylińska, D.K.; Bukowski, R.J.; Bodzenta, J.; Kochowski, S. Thermal Parameters of Solids Determination by the Photodeflection Method—Theories and Experiment Comparison. Opt. Appl. 2008, 38, 445–458. [Google Scholar]
- Kobylińska, D.K.; Bukowski, R.J.; Burak, B.; Bodzenta, J.; Kochowski, S. Photodeflection Signal Formation in Photothermal Measurements: Comparison of the Complex Ray Theory, the Ray Theory, the Wave Theory, and Experimental Results. Appl. Opt. 2007, 46, 5216–5227. [Google Scholar] [CrossRef]
- Lobemeier, M.L. Linearization Plots: Time for Progress in Regression. HMS Beagle 2000, 3, 73. Available online: https://nanopdf.com/download/linearization-plots_pdf (accessed on 25 November 2022).
- Strak, K.; Piasecka, M.; Maciejewska, B. Comparison of the 1D and 2D Calculation Models Used for Determination of the Heat Transfer Coefficient during Flow Boiling Heat Transfer in a Minichannel. E3S Web Conf. 2019, 128, 01017. [Google Scholar] [CrossRef]





| Lens Position, cm | PuB Radius, μm | PuB/PrB Ratio |
|---|---|---|
| 4.7 | 259 | 9.6 |
| 4.8 | 173 | 6.4 |
| 4.9 | 86 | 3.2 |
| 5.0 | 36 | 1.4 |
| 5.1 | 86 | 3.2 |
| 5.2 | 173 | 6.4 |
| 5.3 | 259 | 9.6 |
| 1D Theoretical Model | 2D Theoretical Model | |||
|---|---|---|---|---|
| Lens Position (cm) | DT (×10−2 cm2 s−1) | kT (W m−1 K−1) | DT (×10−2 cm2 s−1) | kT (W m−1 K−1) |
| 4.7 | 94 ± 5 | 243 ± 12 | 92 ± 3 | 238 ± 7 |
| 4.8 | 89 ± 7 | 228 ± 15 | 93 ± 3 | 239 ± 8 |
| 4.9 | 112 ± 9 | 278 ± 22 | 97 ± 4 | 249 ± 8 |
| 5.0 | 125 ± 9 | 312 ± 25 | 95 ± 4 | 241 ± 7 |
| 5.1 | 108 ± 8 | 271 ± 21 | 92 ± 3 | 237 ± 6 |
| 5.2 | 87 ± 7 | 226 ± 16 | 92 ± 2 | 234 ± 6 |
| 5.3 | 95 ± 5 | 244 ± 12 | 93 ± 3 | 240 ± 5 |
| Lens Position, cm | σDT, % | σkT, % |
|---|---|---|
| 4.7 | 2 | 2 |
| 4.8 | 5 | 4 |
| 4.9 | 18 | 16 |
| 5.0 | 32 | 30 |
| 5.1 | 16 | 17 |
| 5.2 | 4 | 4 |
| 5.3 | 2 | 2 |
| 1D Theoretical Model | ||||
|---|---|---|---|---|
| Lens Position, (cm) | RSDDT (%) | RSDkT (%) | Sum of Amplitude Residues (V) | Sum of Phase Residues (Degree) |
| 4.7 | 5.3 | 4.9 | 0.585 | 193 |
| 4.8 | 7.9 | 6.6 | 0.783 | 234 |
| 4.9 | 8.1 | 7.9 | 1.277 | 289 |
| 5.0 | 7.2 | 8.0 | 1.992 | 304 |
| 5.1 | 7.4 | 7.8 | 1.432 | 295 |
| 5.2 | 8.0 | 7.1 | 0.806 | 262 |
| 5.3 | 5.6 | 5.4 | 0.531 | 241 |
| 2D Theoretical Model | ||||
| Lens Position, (cm) | RSDDT (%) | RSDkT (%) | Sum of Amplitude Residues (V) | Sum of Phase Residues (Degree) |
| 4.7 | 3.3 | 2.9 | 0.443 | 158 |
| 4.8 | 3.2 | 3.3 | 0.285 | 112 |
| 4.9 | 4.1 | 3.2 | 0.322 | 118 |
| 5.0 | 4.2 | 2.9 | 0.413 | 151 |
| 5.1 | 3.3 | 2.6 | 0.387 | 124 |
| 5.2 | 2.2 | 2.6 | 0.436 | 153 |
| 5.3 | 3.2 | 2.1 | 0.279 | 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swapna, M.N.S.; Korte, D.; Sankararaman, S.I. Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach. Photonics 2022, 9, 991. https://doi.org/10.3390/photonics9120991
Swapna MNS, Korte D, Sankararaman SI. Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach. Photonics. 2022; 9(12):991. https://doi.org/10.3390/photonics9120991
Chicago/Turabian StyleSwapna, Mohanachandran Nair Sindhu, Dorota Korte, and Sankaranarayana Iyer Sankararaman. 2022. "Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach" Photonics 9, no. 12: 991. https://doi.org/10.3390/photonics9120991
APA StyleSwapna, M. N. S., Korte, D., & Sankararaman, S. I. (2022). Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach. Photonics, 9(12), 991. https://doi.org/10.3390/photonics9120991







