An All-MRR-Based Photonic Spiking Neural Network for Spike Sequence Learning
Abstract
:1. Introduction
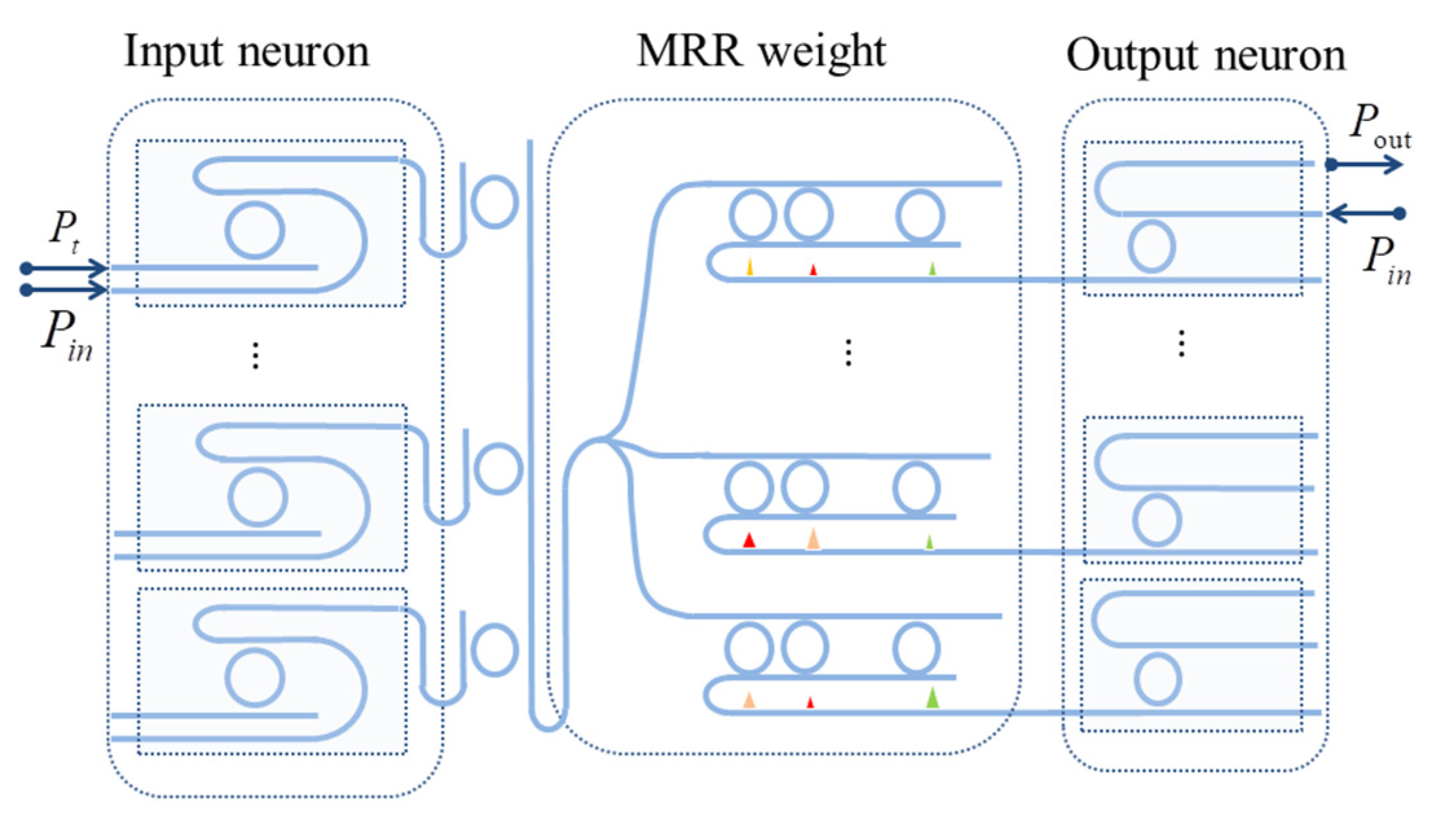
2. System-Level Computational Model
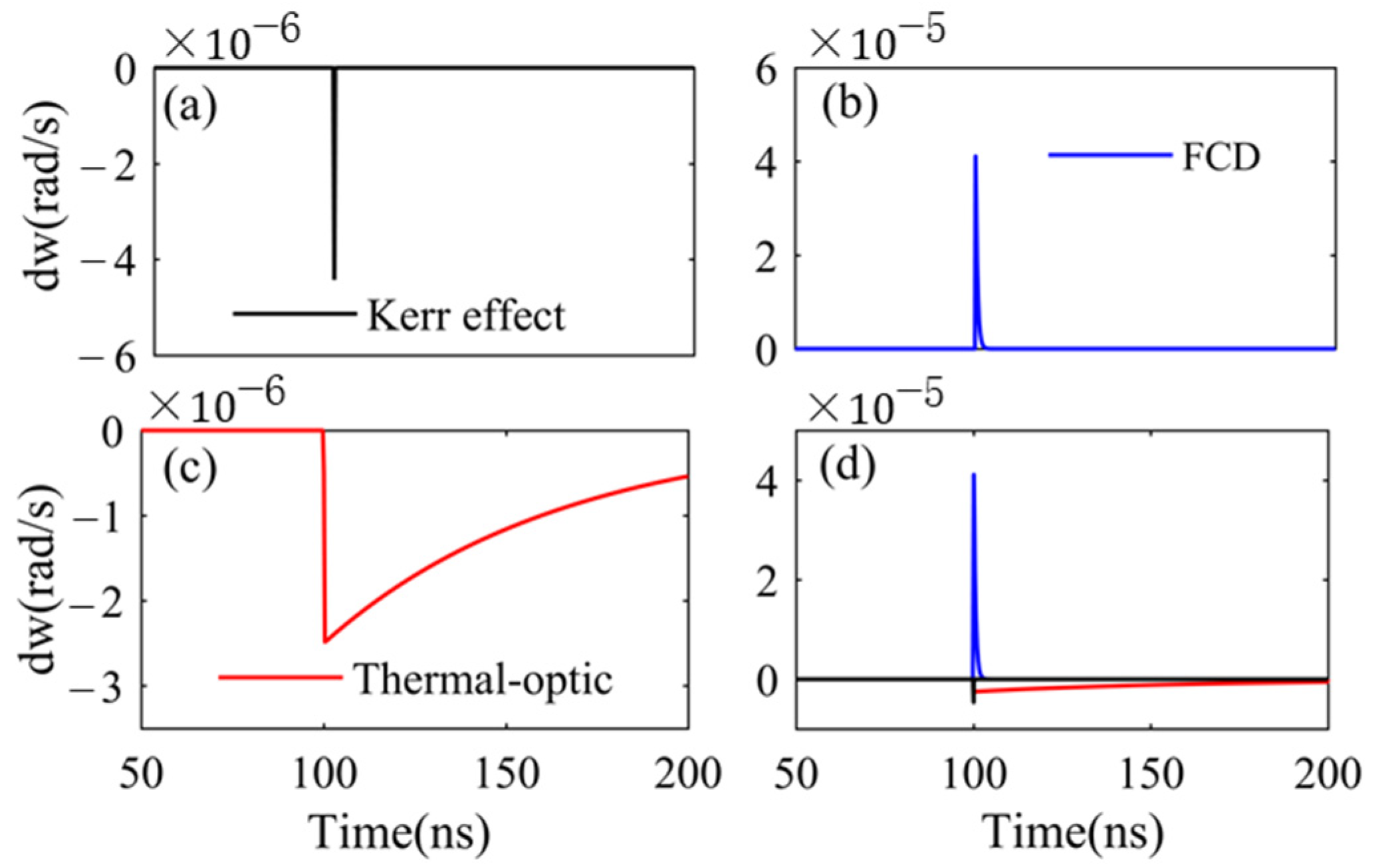
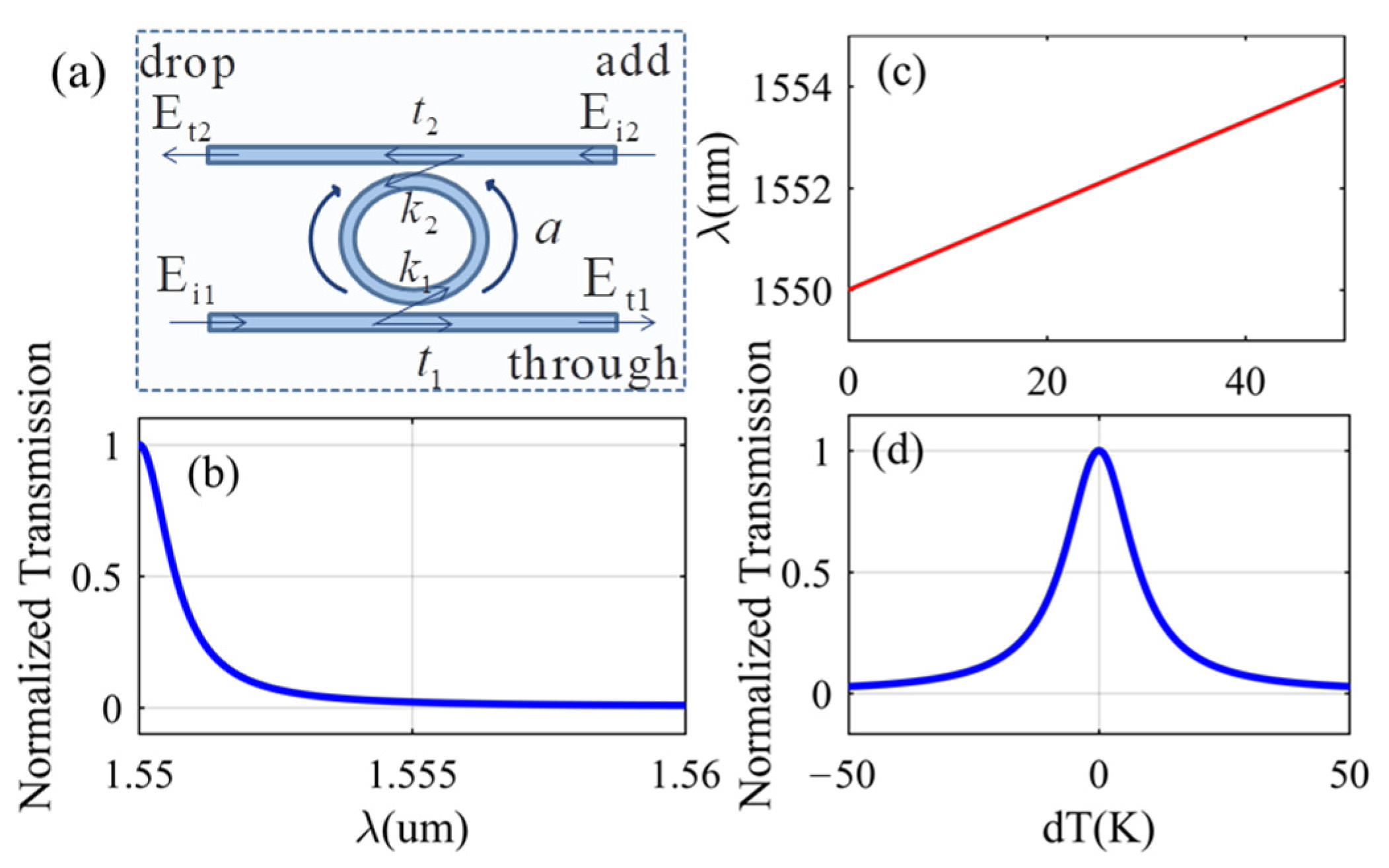
2.1. MRR-Based Photonic Neuron
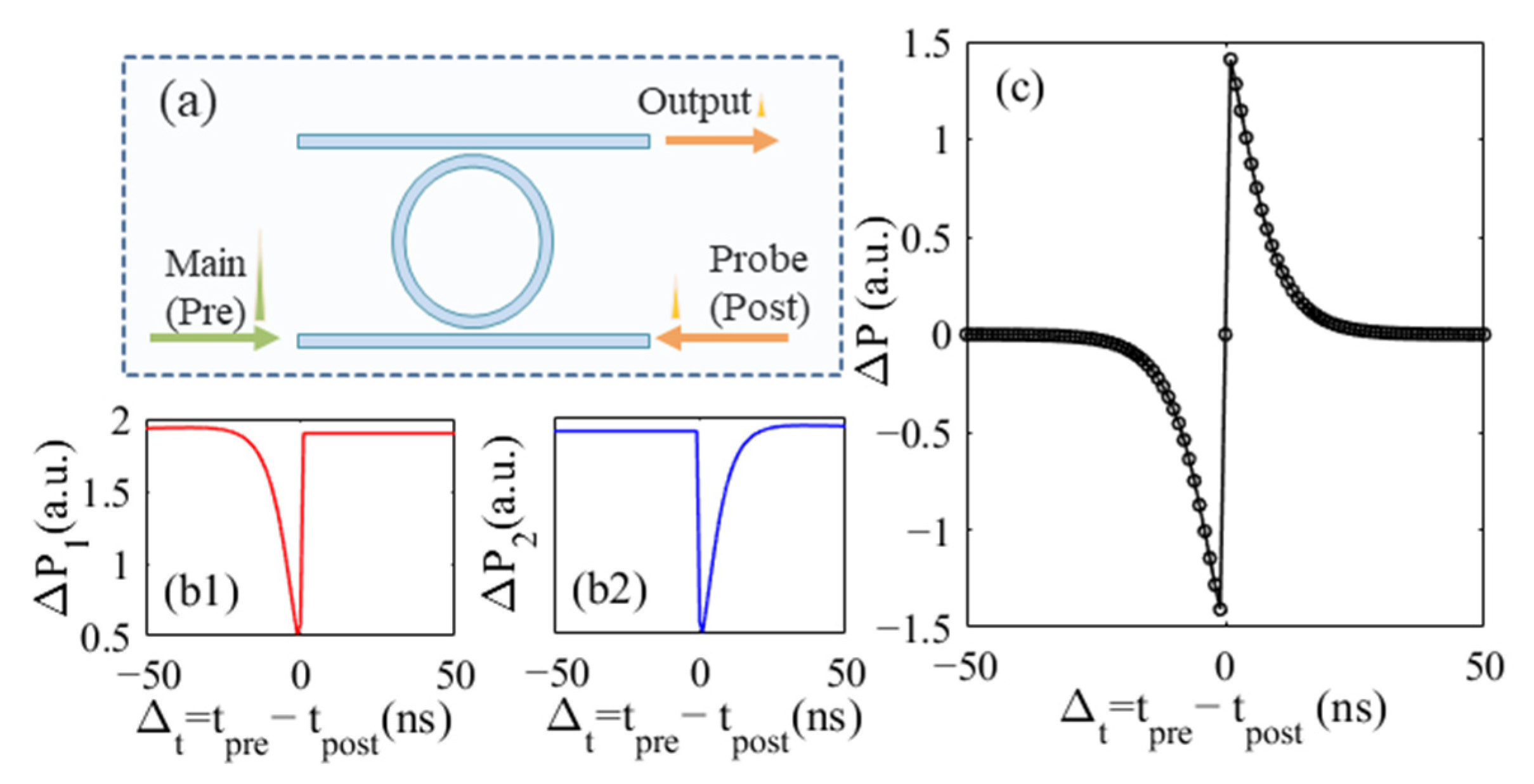
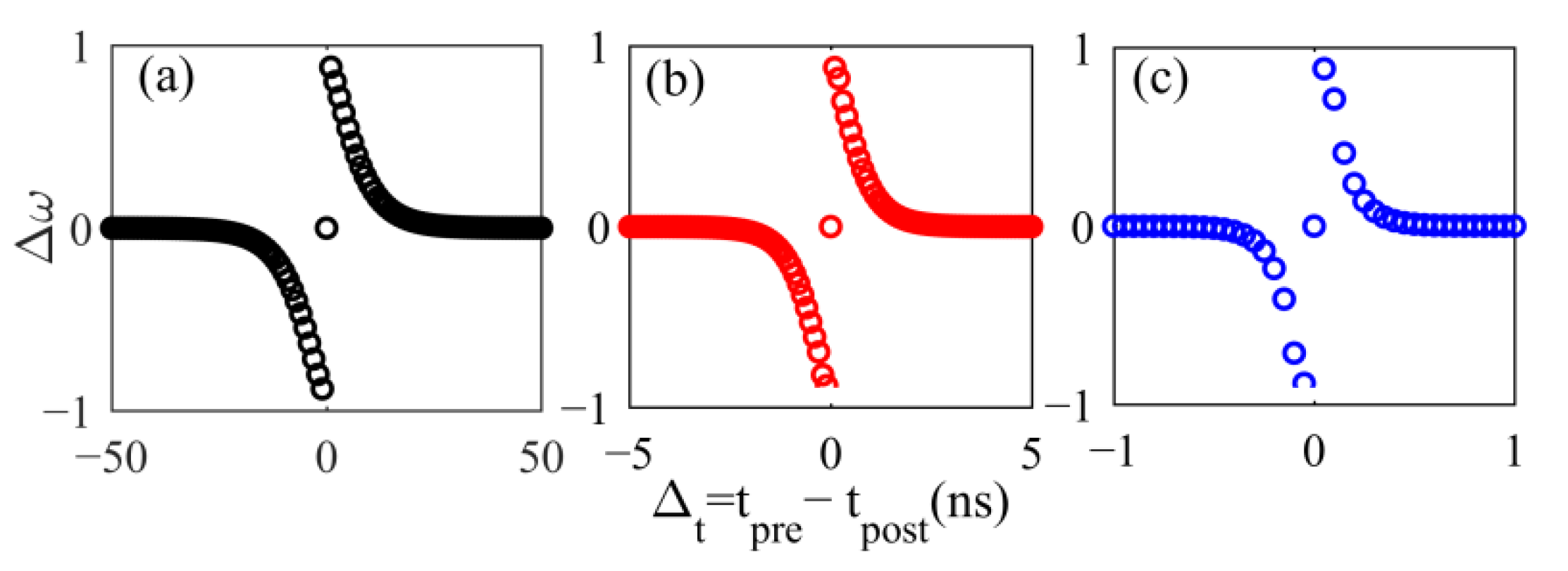
2.2. MRR-Based Optical Synaptic Plasticity
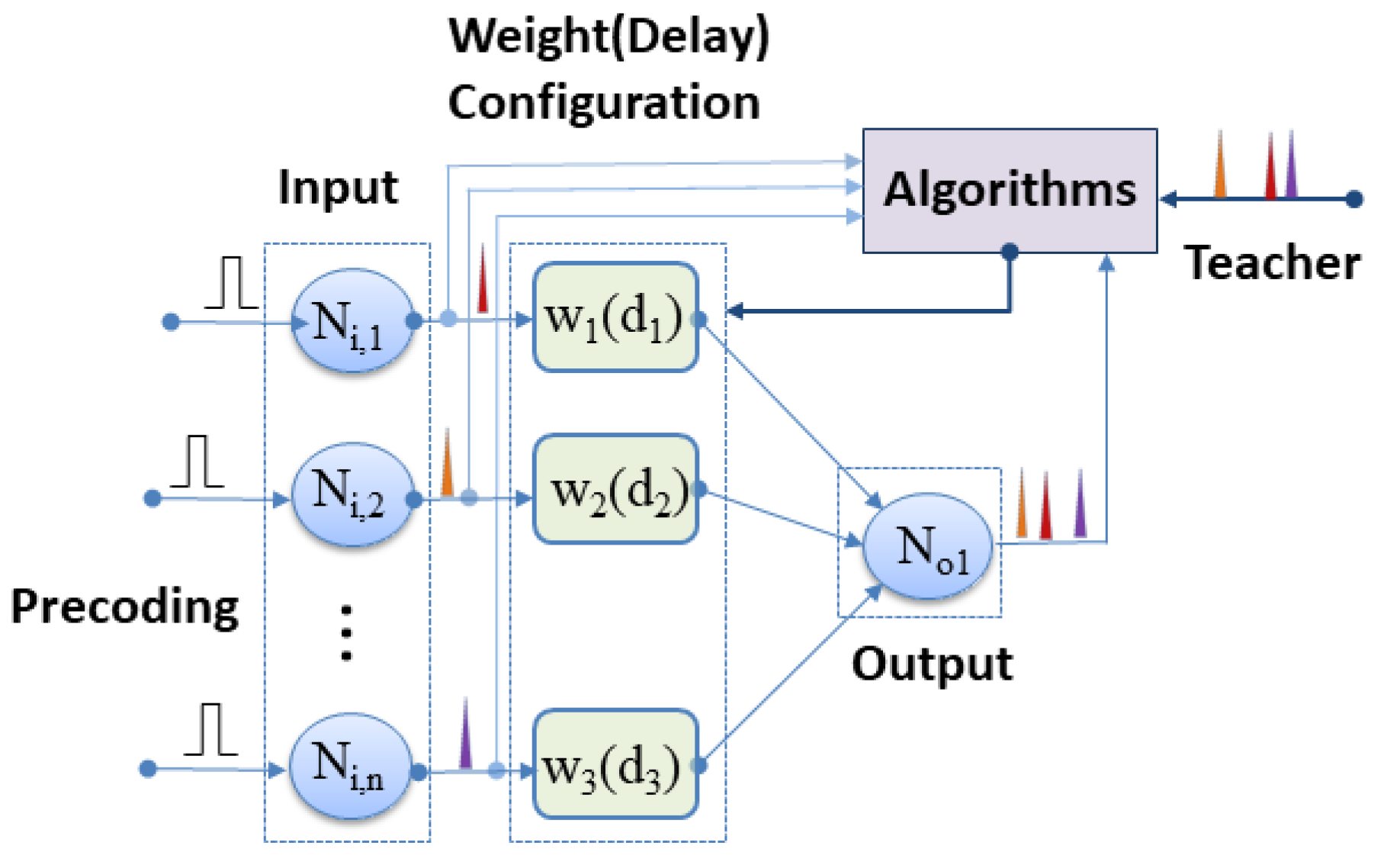
2.3. MRR Based Weight Configuration
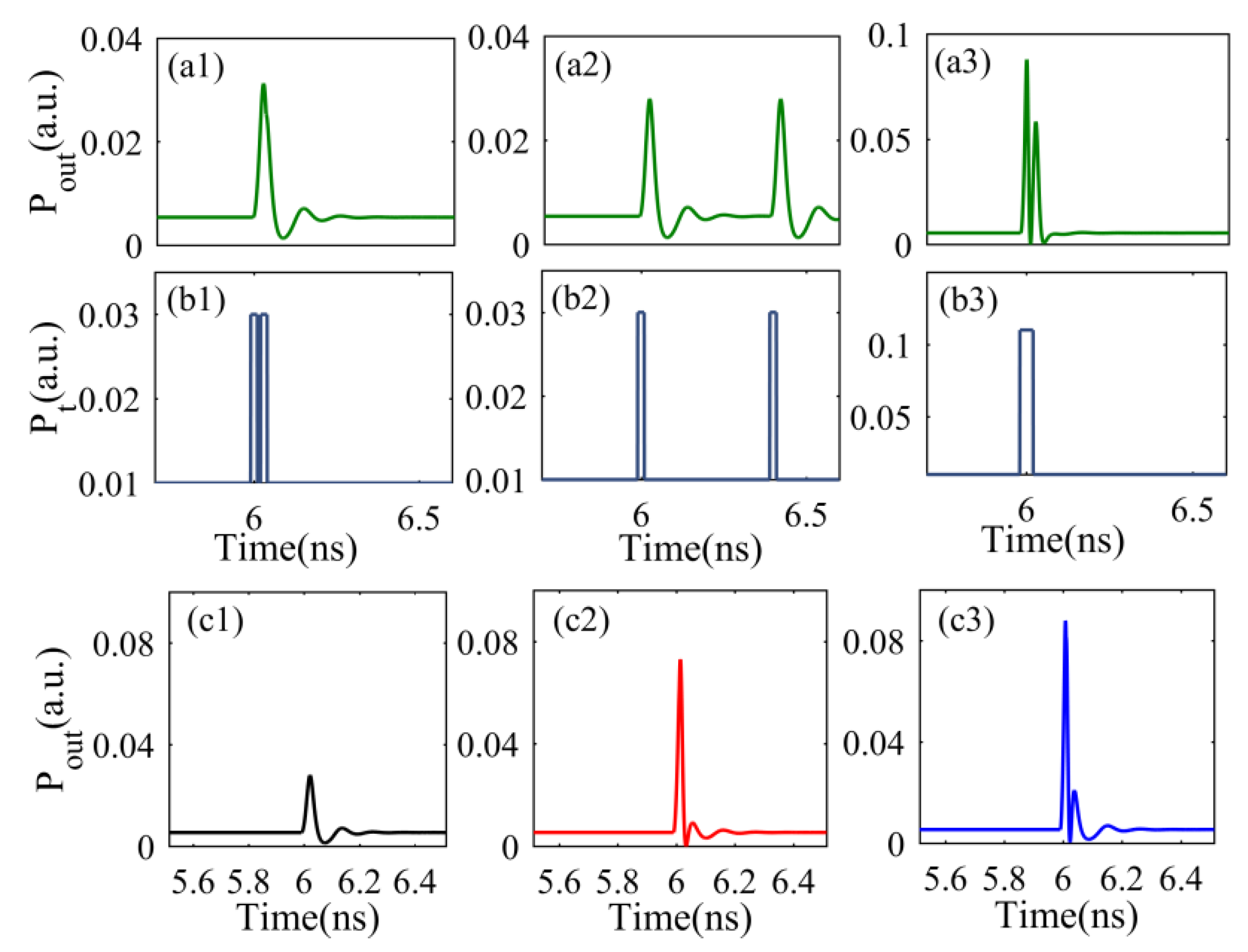
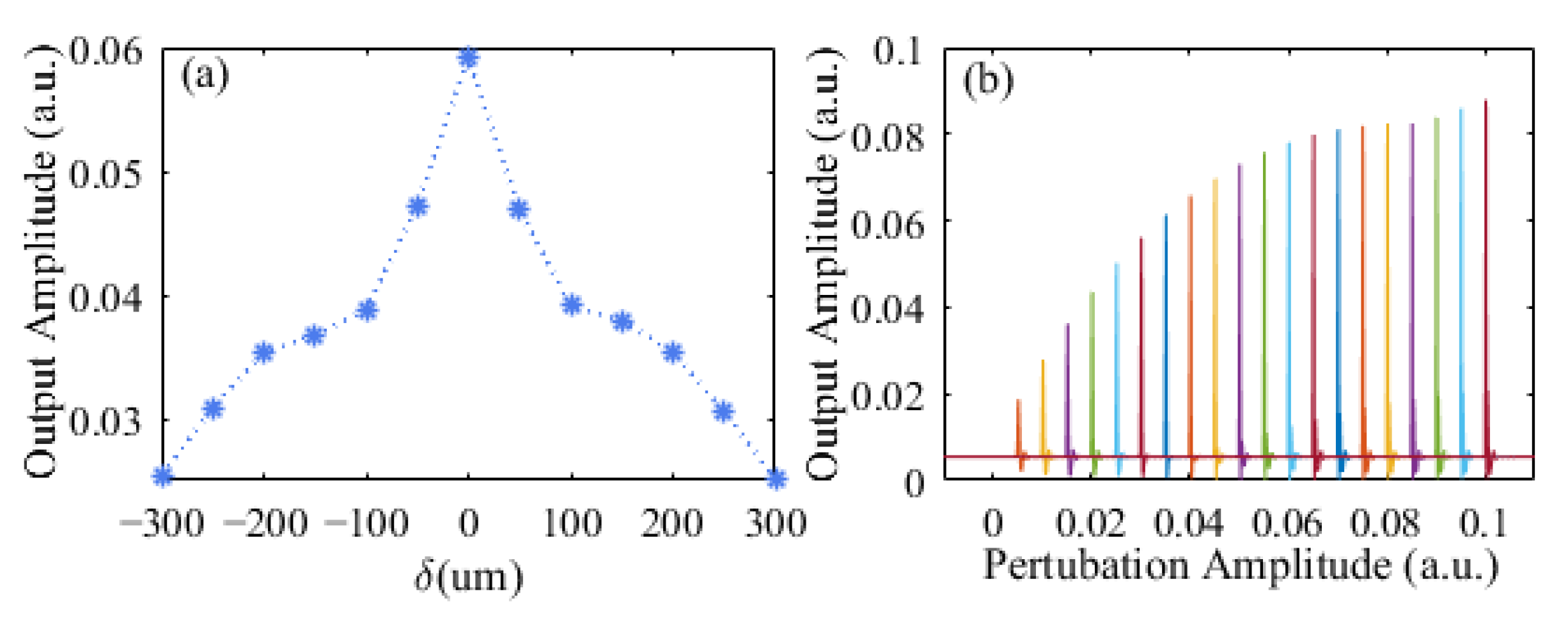
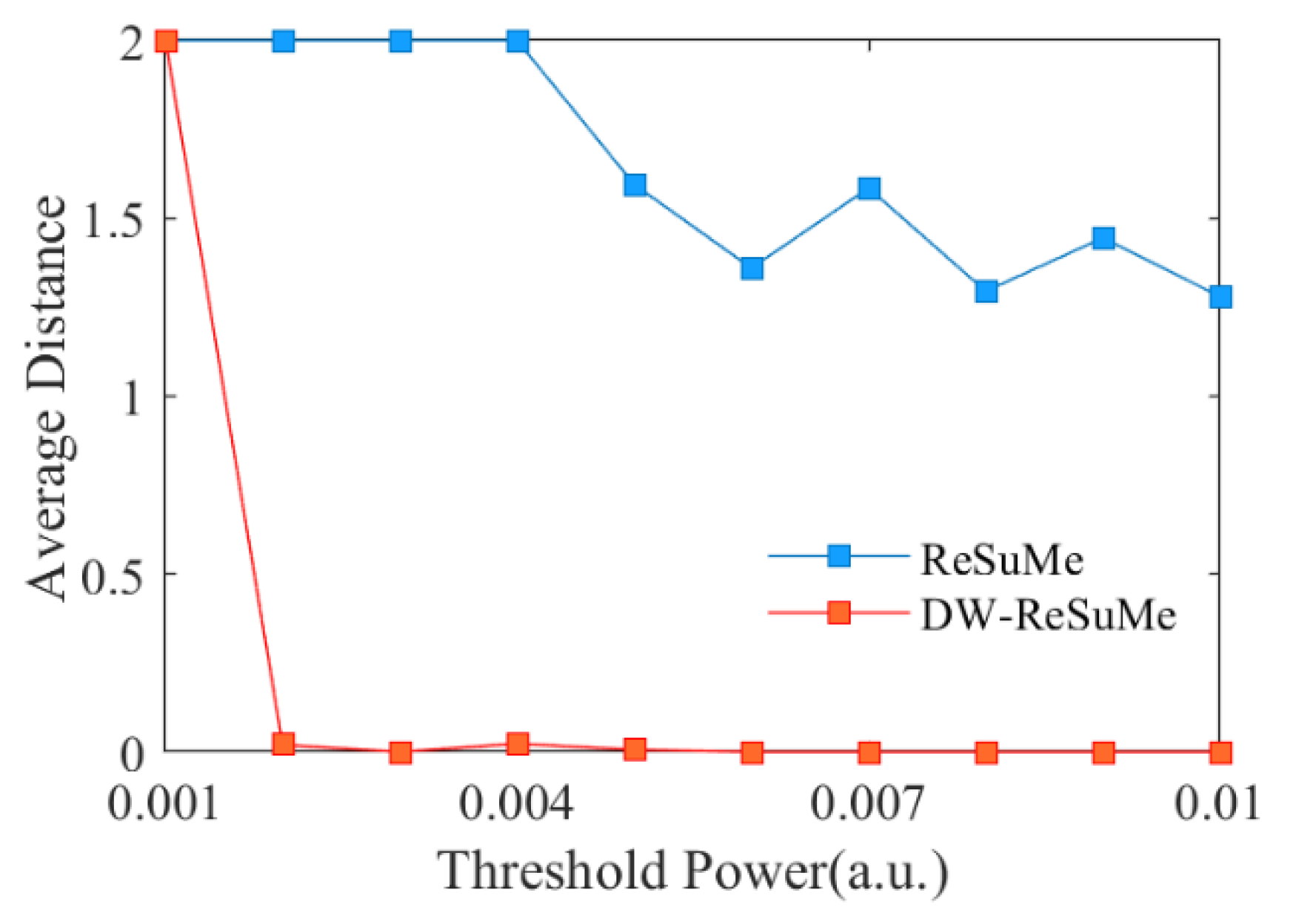
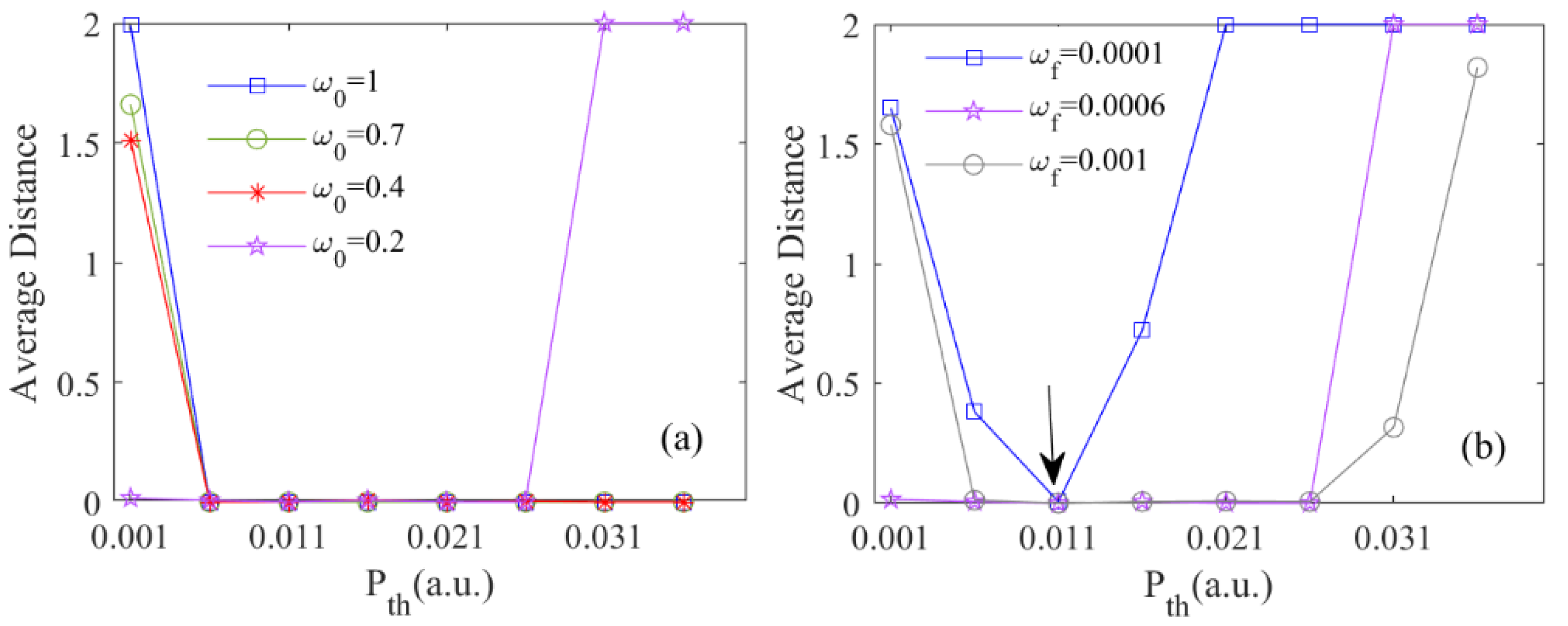
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Furber, S.B.; Galluppi, F.; Temple, S.; Plana, L.A. The SpiNNaker project. Proc. IEEE 2014, 102, 652–665. [Google Scholar] [CrossRef]
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.; et al. TrueNorth: Design and tool flow of a 65 mW 1 million neuron programmable neurosynaptic chip. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, Toronto, ON, Canada, 24–28 June 2017. [Google Scholar]
- Hurtado, A.; Schires, K.; Henning, I.D.; Adams, M.J. Investigation of vertical cavity surface emitting laser dynamics for neuromorphic photonic systems. Appl. Phys. Lett. 2012, 100, 103703. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Wang, Z.; Le, Y.; Sun, C.; Song, X.; Wu, C. Optical implementation of neural learning algorithms based on cross-gain modulation in a semiconductor optical amplifier. Proc. SPIE 2016, 10019, 1–7. [Google Scholar]
- Xiang, S.Y.; Zhang, H.; Guo, X.X.; Li, J.F.; Wen, A.J.; Pan, W.; Hao, Y. Cascadable neuron-Like spiking dynamics in coupled VCSELs subject to orthogonally polarized optical pulse injection. IEEE J. Sel. Topics Quantum Electron. 2017, 23, 1700207. [Google Scholar] [CrossRef]
- Deng, T.; Robertson, J.; Hurtado, A. Controlled propagation of spiking dynamics in vertical-cavity surface-emitting lasers: Towards neuromorphic photonic networks. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1800408. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.G.; Carlos, R.; Pernice, W.H.P.; Wright, C.D.; Bhaskara, H. On-chip photonic synapse. Sci. Adv. 2017, 3, e1700160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ríos, C.; Youngblood, N.; Cheng, Z.G.; Gallo, M.L.; Pernice, W.H.P.; Wright, C.D.; Sebastian, A.; Bhaskaran, H. In-memory computing on a photonic platform. Sci. Adv. 2019, 5, eaau5759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chakraborty, I.; Saha, G.; Roy, K. Photonic in-memory computing primitive for spiking neural networks using phase-change materials. Phys. Rev. Appl. 2019, 11, 014063. [Google Scholar] [CrossRef] [Green Version]
- Xiang, S.Y.; Zhang, Y.H.; Gong, J.K.; Guo, X.X.; Lin, L.; Hao, Y. STDP-based unsupervised spike pattern learning in a photonic spiking neural network with VCSELs and VCSOAs. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1700109. [Google Scholar] [CrossRef]
- Xiang, S.Y.; Ren, Z.X.; Song, Z.W.; Zhang, Y.H.; Guo, X.X.; Han, G.Q.; Hao, Y. Computing primitive of fully-VCSELs-based all-optical spiking neural network for supervised learning and pattern classification. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2494–2505. [Google Scholar] [CrossRef] [PubMed]
- Pammi, V.A.; Alfaro-Bittner, K.; Clerc, M.G.; Barbay, S. Photonic computing with single and coupled spiking micropillar lasers. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1500307. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.H.; Xiang, J.L.; Zhang, Y.J.; Su, Y.K. Integrated neuromorphic photonics: Synapses, neurons, and neural networks. Adv. Photonics Res. 2021, 2, 2000212. [Google Scholar] [CrossRef]
- Han, Y.N.; Xiang, S.Y.; Ren, Z.X.; Fu, C.T.; Wen, A.J.; Hao, Y. Delay-weight plasticity-based supervised learning in optical spiking neural networks. Photonics Res. 2021, 9, B119–B127. [Google Scholar] [CrossRef]
- Shastri, B.J.; Tait, A.N.; de Lima, T.F.; Pernice, W.H.P.; Bhaskaran, H.; Wright, C.D.; Prucnal, P.R. Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 2021, 15, 102–114. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Cui, C.; Li, R.Q.; Li, Y.; Liu, B.; Wu, C.Q. Simulating the spiking response of VCSEL-based optical spiking neuron. Opt. Commun. 2018, 407, 327–332. [Google Scholar] [CrossRef]
- Mesaritakis, C.; Kapsalis, A.; Bogris, A.; Syvridis, D. Artificial neuron based on integrated semiconductor quantum dot mode-locked lasers. Sci. Rep. 2016, 6, 39317. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Xiang, S.Y.; Guo, X.X.; Wen, A.J.; Hao, Y. All-optical inhibitory dynamics in photonic neuron based on polarization mode competition in a VCSEL with an embedded saturable absorber. Opt. Lett. 2019, 44, 1548–1551. [Google Scholar] [CrossRef]
- Ren, Q.; Zhang, Y.; Wang, R.; Zhao, J. Optical spike-timing-dependent plasticity with weight-dependent learning window and reward modulation. Opt. Express 2015, 23, 25247–25258. [Google Scholar] [CrossRef]
- Xiang, S.Y.; Gong, J.K.; Zhang, Y.H.; Guo, X.X.; Wen, A.J.; Hao, Y. Numerical implementation of wavelength-dependent photonic spike timing dependent plasticity based on VCSOA. IEEE J. Quantum Electron. 2018, 54, 8100107. [Google Scholar] [CrossRef]
- Caporale, N.; Yang, D. Spike timing-dependent plasticity: A hebbian learning rule. Annu. Rev. Neurosci. 2008, 31, 25–46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bi, G.-Q.; Poo, M.-M. Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 1998, 18, 10464–10472. [Google Scholar] [CrossRef] [PubMed]
- Ferré, P.; Mamalet, F.; Thorpe, S.J. Unsupervised feature learning with winner-takes-all based STDP. Front. Comput. Neurosci. 2018, 12, 00024. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kheradpisheh, S.R.; Ganjtabesh, M.; Thorpe, S.J.; Masquelier, T. STDP-based spiking deep convolutional neural networks for object recognition. Neural Netw. 2018, 99, 56–67. [Google Scholar] [CrossRef] [Green Version]
- Taherkhani, A.; Belatreche, A.; Li, Y.; Maguire, L.P. A supervised learning algorithm for learning precise timing of multiple spikes in multilayer spiking neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5394–5407. [Google Scholar] [CrossRef] [Green Version]
- Brehm, M. Silicon Photonics IV—Innovative Frontiers; Lockwood, D.J., Pavesi, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–103. [Google Scholar]
- Carrillo, S.G.-C.; Lugnan, A.; Gemo, E.; Bienstman, P.; Pernice, W.H.P.; Bhaskaran, H.; Wright, C.D. System-level simulation for integrated phase-change photonics. J. Light. Technol. 2021, 39, 6392–6402. [Google Scholar] [CrossRef]
- Zhang, W.F.; Yao, J.P. A fully reconfigurable waveguide Bragg grating for programmable photonic signal processing. Nat. Commun. 2018, 9, 1396. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, M.; Jiang, X.D.; Thompson, J.; Cai, H.; Paesani, S.; Santagati, R.; Laing, A.; Zhang, Y.; Yung, M.H.; et al. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 2021, 12, 457. [Google Scholar] [CrossRef]
- Xu, X.Y.; Tan, M.X.; Corcoran, B.; Wu, J.Y.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Karpov, M.; Gehring, H.; Li, X.; Stappers, M.; Gallo, M.L.; Fu, X.; Lukashchuk, A.; Raja, A.S. Parallel convolutional processing using an integrated photonic tensor core. Nature 2021, 589, 52–58. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214. [Google Scholar] [CrossRef] [Green Version]
- Mesaritakis, C.; Skontranis, M.; Sarantoglou, G.; Bogris, A. Micro-ring-resonator based passive photonic spike-time-dependent-plasticity scheme for unsupervised learning in optical neural networks. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020. [Google Scholar]
- Grillanda, S.; Carminati, M.; Morichetti, F.; Ciccarella, P.; Annoni, A.; Ferrari, G.; Strain, M.; Sorel, M.; Sampietro, M.; Melloni, A. Non-invasive monitoring and control in silicon photonics using CMOS integrated electronics. Optica 2014, 1, 129–136. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, Y.; Feng, S.Q.; Poon, A.W. Towards adaptively tuned silicon microring resonators for optical networks-on-chip applications. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 136–149. [Google Scholar] [CrossRef]
- Li, Y.; Poon, A.W. Active resonance wavelength stabilization for silicon microring resonators with an in-resonator defect-state-absorption-based photodetector. Opt. Express 2015, 23, 360–372. [Google Scholar] [CrossRef] [PubMed]
- Poulton, C.V.; Dong, P.; Chen, Y.K. Photo resistive micro ring heater with resonance control loop. In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 10–15 May 2015; Optical Society of America: Holmdel, NJ, USA, 2015; p. SM2I.3. [Google Scholar]
- Hasitha, J.; Kyle, M.; Guillén-Torres, M.A.; Michael, C.; Ricky, H.; Jaeger, N.A.F.; Chrostowski, L.; Shekhar, S. Wavelength tuning and stabilization of microring-based filters using silicon in-resonator photoconductive heaters. Opt. Express 2015, 23, 25084–25097. [Google Scholar]
- Pintus, P.; Hofbauer, M.; Manganelli, C.L.; Fournier, M.; Gundavarapu, S.; Lemonnier, O.; Gambini, F.; Adelmini, L.; Meinhart, C.; Kopp, C.; et al. PWM-driven thermally tunable silicon microring resonators: Design, fabrication, and characterization. Laser Photonics Rev. 2019, 13, 1800275. [Google Scholar] [CrossRef]
- Bangari, V.; Marquez, B.A.; Miller, H.; Tait, A.N.; Nahmias, M.A.; De Lima, T.F.; Peng, H.-T.; Prucnal, P.R.; Shastri, B.J. Digital electronics and analog photonics for convolutional neural networks (DEAP-CNNs). IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Sunny, F.; Mirza, A.; Nikdast, M.; Pasricha, S. CrossLight: A cross-layer optimized silicon photonic neural network accelerator. arXiv 2021, arXiv:2102.06960. [Google Scholar]
- Tait, A.N.; de Lima, T.F.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Multi-channel control for microring weight banks. Opt. Express 2016, 24, 008895. [Google Scholar] [CrossRef]
- Zhang, W.P.; Huang, C.R.; Bilodeau, S.; Jha, A.; Blow, E.; De Lima, T.F.; Shastri, B.J.; Prucnal, P. Microring weight banks control beyond 8.5-bits accuracy. arXiv 2021, arXiv:2104.01164. [Google Scholar]
- Jiang, Y.; Zhang, W.J.; Yang, F.; He, Z.Y. Photonic convolution neural network based on interleaved time-wavelength modulation. J. Light. Technol. 2021, 39, 4592–4600. [Google Scholar] [CrossRef]
- Chakraborty, I.; Saha, G.; Sengupta, A.; Roy, K. Toward fast neural computing using all-photonic phase change spiking neurons. Sci. Rep. 2018, 8, 12980. [Google Scholar] [CrossRef] [PubMed]
- Vaerenbergh, T.V.; Fiers, M.; Mechet, P.; Spuesens, T.; Kumar, R.; Morthier, G.; Schrauwen, B.; Dambre, J.; Bienstman, P. Cascadable excitability in microrings. Opt. Express 2012, 20, 20292–20308. [Google Scholar] [CrossRef] [Green Version]
- Xiang, J.L.; Torchy, A.; Guo, X.H.; Su, Y.K. All-optical spiking neuron based on passive microresonator. J. Light. Technol. 2020, 38, 4019–4029. [Google Scholar] [CrossRef]
- Jha, A.; Huang, C.R.; Peng, H.-T.; Shastri, B.; Prucnal, P.R. Photonic spiking neural networks and CMOS-compatible graphene-on-silicon spiking neurons. arXiv 2021, arXiv:2109.13797v1. [Google Scholar]
- Chen, S.W.; Zhang, L.B.; Fei, Y.H.; Cao, T.T. Bistability and self-pulsation phenomena in silicon microring resonators based on nonlinear optical effects. Opt. Express 2012, 20, 7454–7468. [Google Scholar] [CrossRef]
- Malaguti, S.; Bellanca, G.; de Rossi, A.; Combrié, S.; Trillo, S. Self-pulsing driven by two-photon absorption in semiconductor nanocavities. Phys. Rev. A 2011, 83, 051802. [Google Scholar] [CrossRef]
- Priem, G.; Dumon, P.; Bogaerts, W.; Thourhout, D.V.; Morthier, G.; Baets, R. Optical bistability and pulsating behaviour in Silicon-On-Insulator ring resonator structures. Opt. Express 2005, 13, 9623. [Google Scholar] [CrossRef] [Green Version]
- Haus, H.A.; Popović, M.A.; Watts, R.M.; Manolatou, C.; Little, E.B.; Chu, T.S. Optical resonators and filters. In Optical Microcavities; Advanced Series in Applied Physics; California Institute of Technology: California, CA, USA, 2004; pp. 1–37. [Google Scholar]
- Vermeulen, N.; David, C.L.; Cheng, J.L.; Pasternak, I.; Krajewska, A.; Ciuk, T.; Strupinski, W.; Thienpont, H.; Erps, J.V. Negative Kerr nonlinearity of graphene as seen via chirped-pulse-pumped self-phase modulation. Phys. Rev. Appl. 2016, 6, 044006. [Google Scholar] [CrossRef]
- Ataloglou, V.G.; Christopoulos, T.; Kriezis, E.E. Nonlinear coupled-mode theory framework for graphene-induced saturable absorption in nanophotonic resonant structures. Phys. Rev. A 2018, 97, 063836. [Google Scholar] [CrossRef]
- Chatzidimitriou, D.; Pitilakisa, A.; Kriezis, E.E. Rigorous calculation of nonlinear parameters in graphene-comprising waveguides. J. Appl. Phys. 2015, 118, 023105. [Google Scholar] [CrossRef] [Green Version]
- Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; The MIT Press: Cambridge, MA, USA; London, UK, 2007. [Google Scholar]
- FitzHugh, R. Mathematical models of threshold phenomena in the nerve membrane. Bull. Math. Biol. 1955, 17, 257–278. [Google Scholar] [CrossRef]
- Lin, Q.; Johnson, T.J.; Michael, C.P.; Painter, O. Adiabatic self-tuning in a silicon microdisk optical resonator. Opt. Express 2008, 16, 14801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Froemke, R.; Dan, Y. Spike-timing dependent plasticity induced by natural spike trains. Nature 2002, 416, 433–438. [Google Scholar] [CrossRef] [PubMed]
- Pfister, J.P.; Gerstner, W. Triplets of Spikes in a Model of Spike Timing-Dependent Plasticity. J. Neurosci. 2006, 26, 9673–9682. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Xiang, S.; Zhang, Y.; Gao, S.; Wen, A.; Hao, Y. An All-MRR-Based Photonic Spiking Neural Network for Spike Sequence Learning. Photonics 2022, 9, 120. https://doi.org/10.3390/photonics9020120
Han Y, Xiang S, Zhang Y, Gao S, Wen A, Hao Y. An All-MRR-Based Photonic Spiking Neural Network for Spike Sequence Learning. Photonics. 2022; 9(2):120. https://doi.org/10.3390/photonics9020120
Chicago/Turabian StyleHan, Yanan, Shuiying Xiang, Yuna Zhang, Shuang Gao, Aijun Wen, and Yue Hao. 2022. "An All-MRR-Based Photonic Spiking Neural Network for Spike Sequence Learning" Photonics 9, no. 2: 120. https://doi.org/10.3390/photonics9020120
APA StyleHan, Y., Xiang, S., Zhang, Y., Gao, S., Wen, A., & Hao, Y. (2022). An All-MRR-Based Photonic Spiking Neural Network for Spike Sequence Learning. Photonics, 9(2), 120. https://doi.org/10.3390/photonics9020120





