Two-Colour Sum-Frequency Generation Spectroscopy Coupled to Plasmonics with the CLIO Free Electron Laser
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
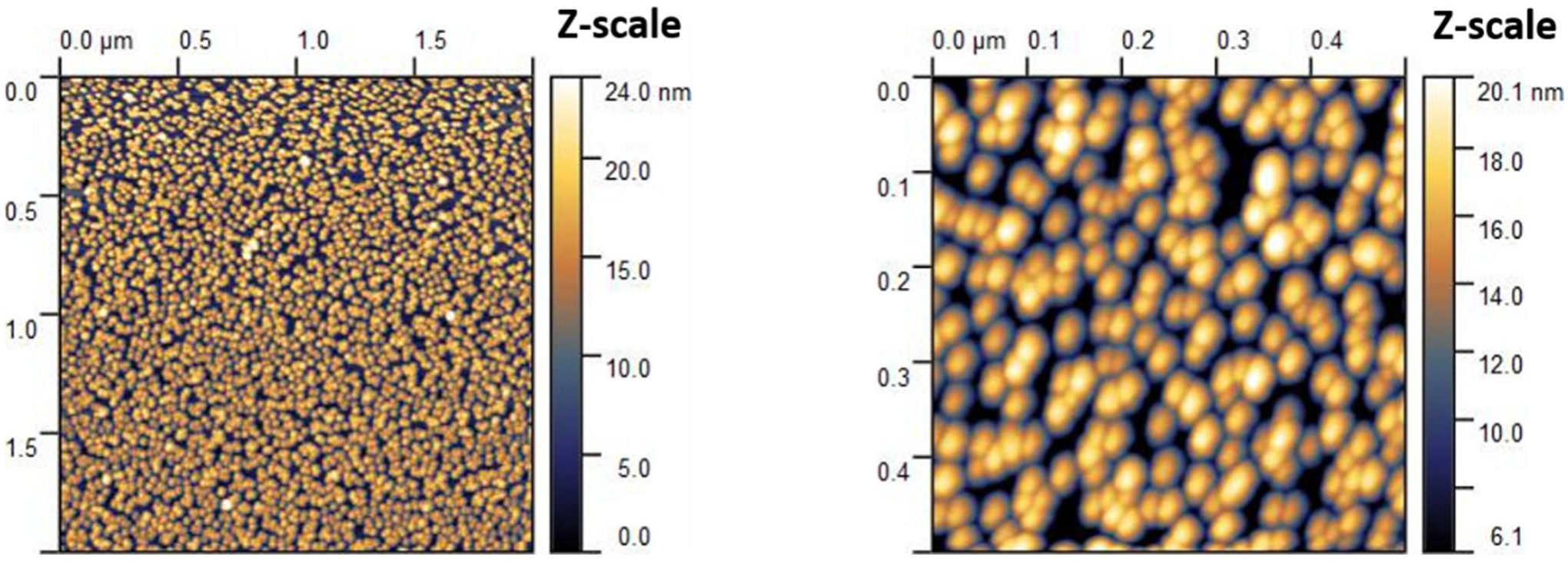
2.2. AFM Microscopy
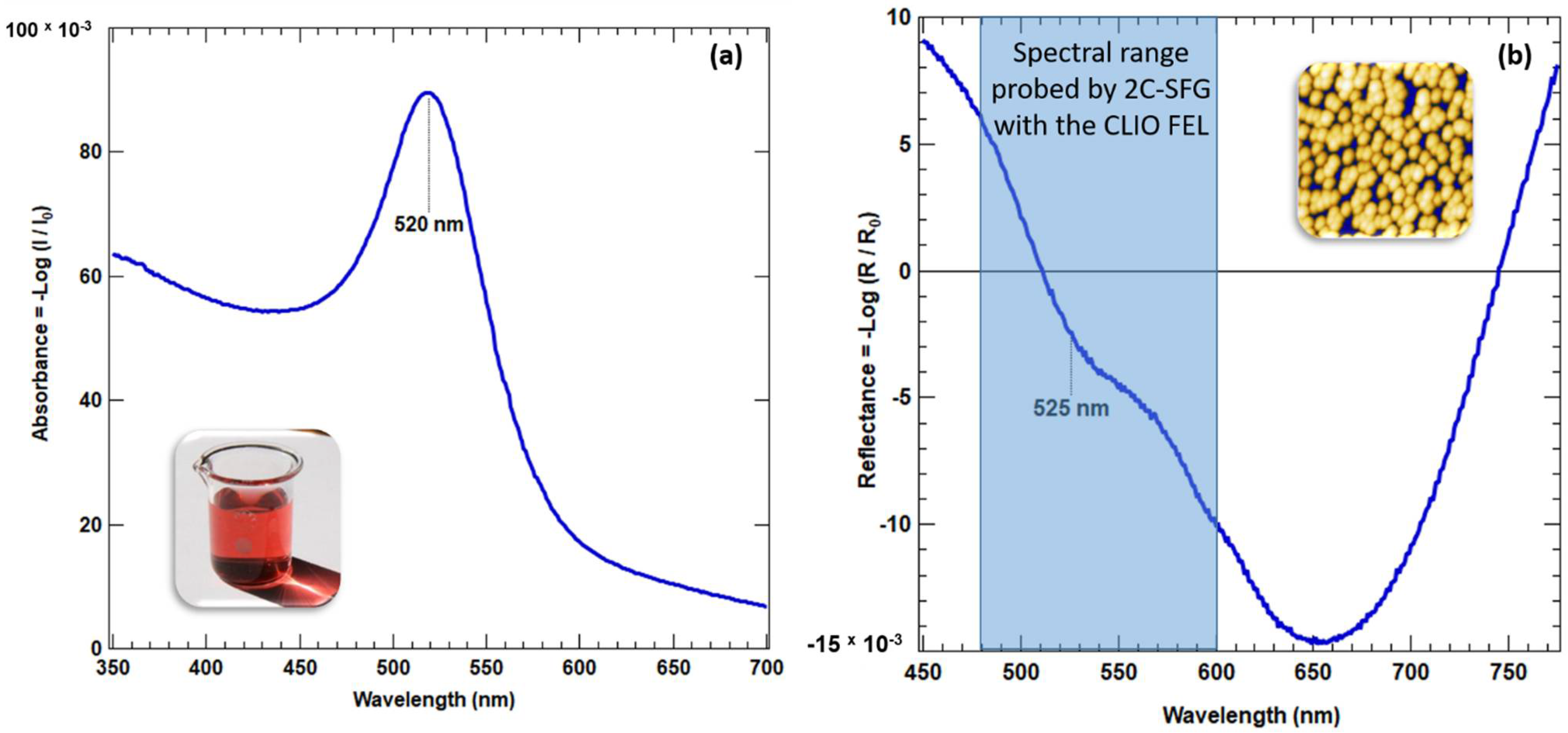
2.3. UV-Vis Spectroscopy
2.4. 2C-SFG Spectroscopy with the CLIO Free Electron Laser Facility
3. Results
3.1. AFM Characterisation
3.2. UV-Visible Measurements
3.3. 2C-SFG Measurements
4. Discussion
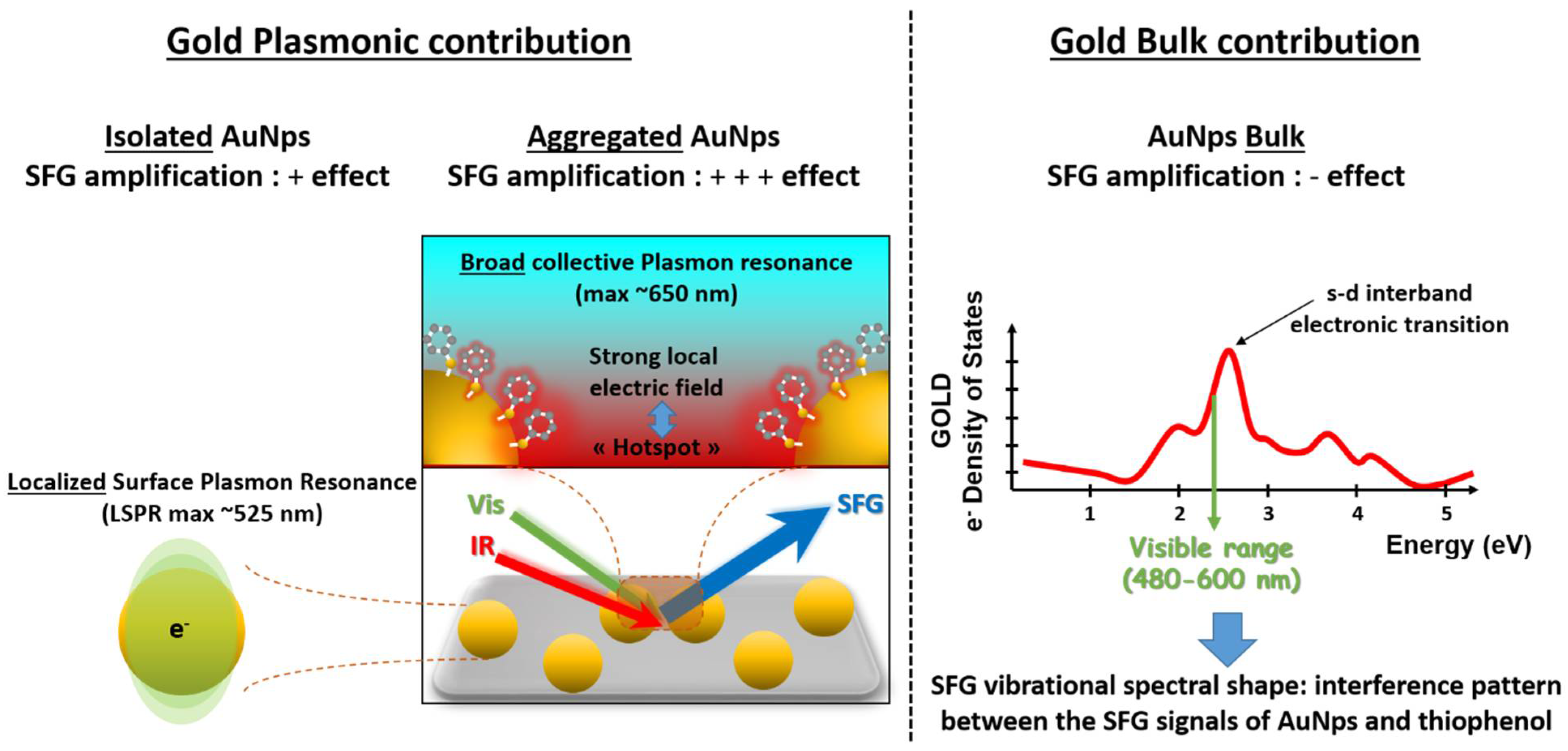
4.1. Phase Shift Parameter: Gold s-d Interband Electronic Transitions
4.2. Co- vs. Counter-Propagating Geometry: SFG Spectra Shape Reversal
4.3. Amplification of Thiophenol Vibration Modes: Collective Plasmon Modes Coupling
4.4. Technical Prospects for 2C-SFG Spectroscopy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dalstein, L.; Humbert, C.; Ben Haddada, M.; Boujday, S.; Barbillon, G.; Busson, B. The Prevailing Role of Hotspots in Plasmon-Enhanced Sum-Frequency Generation Spectroscopy. J. Phys. Chem. Lett. 2019, 10, 7706–7711. [Google Scholar] [CrossRef] [Green Version]
- Lis, D.; Caudano, Y.; Henry, M.; Demoustier-Champagne, S.; Ferain, E.; Cecchet, F. Selective Plasmonic Platforms Based on Nanopillars to Enhance Vibrational Sum-Frequency Generation Spectroscopy. Adv. Opt. Mater. 2013, 1, 244–255. [Google Scholar] [CrossRef]
- Lis, D.; Cecchet, F. Localized surface plasmon resonances in nanostructures to enhance nonlinear vibrational spectroscopies: Towards an astonishing molecular sensitivity. Beilstein J. Nanotechnol. 2014, 5, 2275–2292. [Google Scholar] [CrossRef] [PubMed]
- Noblet, T.; Dreesen, L.; Boujday, S.; Méthivier, C.; Busson, B.; Tadjeddine, A.; Humbert, C. Semiconductor quantum dots reveal dipolar coupling from exciton to ligand vibration. Commun. Chem. 2018, 1, 76. [Google Scholar] [CrossRef]
- Noblet, T.; Boujday, S.; Méthivier, C.; Erard, M.; Hottechamps, J.; Busson, B.; Humbert, C. Two-Dimensional Layers of Colloidal CdTe Quantum Dots: Assembly, Optical Properties, and Vibroelectronic Coupling. J. Phys. Chem. C 2020, 124, 25873–25883. [Google Scholar] [CrossRef]
- Sengupta, S.; Bromley, L.; Velarde, L. Aggregated States of Chalcogenorhodamine Dyes on Nanocrystalline Titania Revealed by Doubly Resonant Sum Frequency Spectroscopy. J. Phys. Chem. C 2017, 121, 3424–3436. [Google Scholar] [CrossRef]
- Dreesen, L.; Sartenaer, Y.; Humbert, C.; Mani, A.A.; Lemaire, J.-J.; Méthivier, C.; Pradier, C.-M.; Thiry, P.A.; Peremans, A. Sum-frequency generation spectroscopy applied to model biosensors systems. Thin Solid Films 2004, 464–465, 373–378. [Google Scholar] [CrossRef]
- Humbert, C.; Noblet, T.; Dalstein, L.; Busson, B.; Barbillon, G. Sum-Frequency Generation Spectroscopy of Plasmonic Nanomaterials: A Review. Materials 2019, 12, 836. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Noblet, T.; Dreesen, L.; Tadjeddine, A.; Humbert, C. Spatial dependence of the dipolar interaction between quantum dots and organic molecules probed by two-color sum-frequency generation spectroscopy. Symmetry 2021, 13, 1636. [Google Scholar] [CrossRef]
- Dreesen, L.; Humbert, C.; Sartenaer, Y.; Caudano, Y.; Volcke, C.; Mani, A.A.; Peremans, A.; Thiry, P.A.; Hanique, S.; Frère, J.-M. Electronic and molecular properties of an adsorbed protein monolayer probed by two-color sum-frequency generation spectroscopy. Langmuir 2004, 20, 7201–7207. [Google Scholar] [CrossRef]
- Raab, M.; Becca, J.C.; Heo, J.; Lim, C.K.; Baev, A.; Jensen, L.; Prasad, P.N.; Velarde, L. Doubly resonant sum frequency spectroscopy of mixed photochromic isomers on surfaces reveals conformation-specific vibronic effects. J. Chem. Phys. 2019, 150, 114704. [Google Scholar] [CrossRef] [PubMed]
- Busson, B.; Farhat, M.; Nini Teunda, P.J.; Roy, S.; Jarisz, T.; Hore, D.K. All-experimental analysis of doubly resonant sum-frequency generation spectra: Application to aggregated rhodamine films. J. Chem. Phys. 2021, 154, 224704. [Google Scholar] [CrossRef] [PubMed]
- Peremans, A.; Caudano, Y.; Thiry, P.A.; Dumas, P.; Zhang, W.Q.; Le Rille, A.; Tadjeddine, A. Electronic Tuning of Dynamical Charge Transfer at an Interface: K Doping of C60/Ag(111). Phys. Rev. Lett. 1997, 78, 2999–3002. [Google Scholar] [CrossRef]
- Caudano, Y.; Silien, C.; Humbert, C.; Dreesen, L.; Mani, A.A.; Peremans, A.; Thiry, P.A. Electron-phonon couplings at C60 interfaces: A case study by two-color, infrared-visible sum-frequency generation spectroscopy. J. Electron. Spectros. Relat. Phenom. 2003, 129, 139–147. [Google Scholar] [CrossRef]
- Elsenbeck, D.; Das, S.K.; Velarde, L. Substrate influence on the interlayer electron-phonon couplings in fullerene films probed with doubly-resonant SFG spectroscopy. Phys. Chem. Chem. Phys. 2017, 19, 18519–18528. [Google Scholar] [CrossRef] [Green Version]
- Chou, K.C.; Westerberg, S.; Shen, Y.R.; Ross, P.N.; Somorjai, G.A. Probing the charge-transfer state of CO on Pt(111) by two-dimensional infrared-visible sum frequency generation spectroscopy. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 1–4. [Google Scholar] [CrossRef]
- Busson, B.; Dalstein, L. Sum-Frequency Spectroscopy Amplified by Plasmonics: The Small Particle Case. J. Phys. Chem. C 2019, 123, 26597–26607. [Google Scholar] [CrossRef]
- Dalstein, L.; Ben Haddada, M.; Barbillon, G.; Humbert, C.; Tadjeddine, A.; Boujday, S.; Busson, B. Revealing the Interplay between Adsorbed Molecular Layers and Gold Nanoparticles by Linear and Nonlinear Optical Properties. J. Phys. Chem. C 2015, 119, 17146–17155. [Google Scholar] [CrossRef] [Green Version]
- Linke, M.; Hille, M.; Lackner, M.; Schumacher, L.; Schlücker, S.; Hasselbrink, E. Plasmonic Effects of Au Nanoparticles on the Vibrational Sum Frequency Spectrum of 4-Nitrothiophenol. J. Phys. Chem. C 2019, 123, 24234–24242. [Google Scholar] [CrossRef]
- Kawai, T.; Neivandt, D.J.; Davies, P.B. Sum frequency generation on surfactant-coated gold nanoparticles. J. Am. Chem. Soc. 2000, 122, 12031–12032. [Google Scholar] [CrossRef]
- Tourillon, G.; Dreesen, L.; Volcke, C.; Sartenaer, Y.; Thiry, P.A.; Peremans, A. Total internal reflection sum-frequency generation spectroscopy and dense gold nanoparticles monolayer: A route for probing adsorbed molecules. Nanotechnology 2007, 18, 415301. [Google Scholar] [CrossRef]
- Tourillon, G.; Dreesen, L.; Volcke, C.; Sartenaer, Y.; Thiry, P.A.; Peremans, A. Close-packed array of gold nanoparticles and sum frequency generation spectroscopy in total internal reflection: A platform for studying biomolecules and biosensors. J. Mater. Sci. 2009, 44, 6805–6810. [Google Scholar] [CrossRef]
- Weeraman, C.; Yatawara, A.K.; Bordenyuk, A.N.; Benderskii, A.V. Effect of nanoscale geometry on molecular conformation: Vibrational sum-frequency generation of alkanethiols on gold nanoparticles. J. Am. Chem. Soc. 2006, 128, 14244–14245. [Google Scholar] [CrossRef]
- Bordenyuk, A.N.; Weeraman, C.; Yatawara, A.; Jayathilake, H.D.; Stiopkin, I.; Liu, Y.; Benderskii, A.V. Vibrational sum frequency generation spectroscopy of dodecanethiol on metal nanoparticles. J. Phys. Chem. C 2007, 111, 8925–8933. [Google Scholar] [CrossRef]
- Alyabyeva, N.; Ouvrard, A.; Zakaria, A.M.; Bourguignon, B. Probing Nanoparticle Geometry down to Subnanometer Size: The Benefits of Vibrational Spectroscopy. J. Phys. Chem. Lett. 2019, 10, 624–629. [Google Scholar] [CrossRef]
- Molinaro, C.; Cecchet, F. Label-free, quantitative and sensitive detection of nanoparticle/membrane interactions through the optical response of water. Sens. Actuators B Chem. 2019, 289, 169–174. [Google Scholar] [CrossRef]
- Humbert, C.; Noblet, T. A unified mathematical formalism for first to third order dielectric response of matter: Application to surface-specific two-colour vibrational optical spectroscopy. Symmetry 2021, 13, 153. [Google Scholar] [CrossRef]
- Raschke, M.B.; Hayashi, M.; Lin, S.H.; Shen, Y.R. Doubly-resonant sum-frequency generation spectroscopy for surface studies. Chem. Phys. Lett. 2002, 359, 367–372. [Google Scholar] [CrossRef]
- Dreesen, L.; Humbert, C.; Celebi, M.; Lemaire, J.J.; Mani, A.A.; Thiry, P.A.; Peremans, A. Influence of the metal electronic properties on the sum-frequency generation spectra of dodecanethiol self-assembled monolayers on Pt (111), Ag (111) and Au (111) single crystals. Appl. Phys. B Lasers Opt. 2002, 74, 621–625. [Google Scholar] [CrossRef]
- Carron, K.T.; Hurley, L.G. Axial and azimuthal angle determination with surface-enhanced Raman spectroscopy: Thiophenol on copper, silver, and gold metal surfaces. J. Phys. Chem. 1991, 95, 9979–9984. [Google Scholar] [CrossRef]
- Feugmo, C.G.T.; Liégeois, V. Analyzing the vibrational signatures of thiophenol adsorbed on small gold clusters by DFT calculations. ChemPhysChem 2013, 14, 1633–1645. [Google Scholar] [CrossRef]
- Hosseinpour, S.; Roeters, S.J.; Bonn, M.; Peukert, W.; Woutersen, S.; Weidner, T. Structure and Dynamics of Interfacial Peptides and Proteins from Vibrational Sum-Frequency Generation Spectroscopy. Chem. Rev. 2020, 120, 3420–3465. [Google Scholar] [CrossRef] [PubMed]
- Braun, R.; Casson, B.D.; Bain, C.D.; Van Der Ham, E.W.M.; Vrehen, Q.H.F.; Eliel, E.R.; Briggs, A.M.; Davies, P.B. Sum-frequency generation from thiophenol on silver in the mid and far-IR. J. Chem. Phys. 1999, 110, 4634–4640. [Google Scholar] [CrossRef]
- Bozzini, B.; D’Urzo, L.; Mele, C.; Busson, B.; Humbert, C.; Tadjeddine, A. Doubly resonant sum frequency generation spectroscopy of adsorbates at an electrochemical interface. J. Phys. Chem. C 2008, 112, 11791–11795. [Google Scholar] [CrossRef]
- Bozzini, B.; Abyaneh, M.K.; Busson, B.; Pietro De Gaudenzi, G.; Gregoratti, L.; Humbert, C.; Amati, M.; Mele, C.; Tadjeddine, A. supported Pt-Part III: Monitoring of electrodeposited-Pt catalyst ageing by in situ Fourier transform infrared spectroscopy, in situ sum frequency generation spectroscopy and ex situ photoelectron spectromicroscopy. J. Power Sources 2016, 231, 6–17. [Google Scholar] [CrossRef]
- Kiessling, R.; Tong, Y.; Giles, A.J.; Gewinner, S.; Schöllkopf, W.; Caldwell, J.D.; Wolf, M.; Paarmann, A. Surface Phonon Polariton Resonance Imaging Using Long-Wave Infrared-Visible Sum-Frequency Generation Microscopy. ACS Photonics 2019, 6, 3017–3023. [Google Scholar] [CrossRef] [Green Version]
- Ortega, J.M.; Glotin, F.; Prazeres, R. Extension in far-infrared of the CLIO free-electron laser. Infrared Phys. Technol. 2006, 49, 133–138. [Google Scholar] [CrossRef]
- Pluchery, O.; Humbert, C.; Valamanesh, M.; Lacaze, E.; Busson, B. Enhanced detection of thiophenol adsorbed on gold nanoparticles by SFG and DFG nonlinear optical spectroscopy. Phys. Chem. Chem. Phys. 2009, 11, 7729–7737. [Google Scholar] [CrossRef]
- Humbert, C.; Pluchery, O.; Lacaze, E.; Tadjeddine, A.; Busson, B. A multiscale description of molecular adsorption on gold nanoparticles by nonlinear optical spectroscopy. Phys. Chem. Chem. Phys. 2012, 14, 280–289. [Google Scholar] [CrossRef]
- Humbert, C.; Pluchery, O.; Lacaze, E.; Tadjeddine, A.; Busson, B. Optical spectroscopy of functionalized gold nanoparticles assemblies as a function of the surface coverage. Gold Bull. 2013, 46, 299–309. [Google Scholar] [CrossRef] [Green Version]
- Bain, C.D. Sum-frequency Vibrational Spectroscopy of the Solid/Liquid Interface. J. Chem. Soc. Faraday Trans. 1995, 91, 1281–1296. [Google Scholar] [CrossRef]
- Eliel, E.R.; van der Ham, E.W.M.; Vrehen, Q.H.F. Enhancing the yield in surface sum-frequency generation by the use of surface polaritons. Appl. Phys. B Lasers Opt. 1999, 68, 349–353. [Google Scholar] [CrossRef]
- van der Ham, E.W.M.; Vrehen, Q.H.F.; Eliel, E.R. Self-dispersive sum-frequency generation at interfaces. Opt. Lett. 1996, 21, 1448–1450. [Google Scholar] [CrossRef] [PubMed]
- Mani, A.A.; Dreesen, L.; Humbert, C.; Hollander, P.; Caudano, Y.; Thiry, P.A.; Peremans, A. Development of a two-color picosecond optical parametric oscillator, pumped by a Nd:YAG laser mode locked using a nonlinear mirror, for doubly-resonant sum frequency generation spectroscopy. Surf. Sci. 2002, 502–503, 261–267. [Google Scholar] [CrossRef]
- Grabar, K.C.; Hommer, M.B.; Natan, M.J.; Freeman, R.G. Preparation and Characterization of Au Colloid Monolayers. Anal. Chem. 1995, 67, 735–743. [Google Scholar] [CrossRef]
- Su, K.H.; Wei, Q.H.; Zhang, X.; Mock, J.J.; Smith, D.R.; Schultz, S. Interparticle coupling effects on plasmon resonances of nanogold particles. Nano Lett. 2003, 3, 1087–1090. [Google Scholar] [CrossRef]
- Funston, A.M.; Novo, C.; Davis, T.J.; Mulvaney, P. Plasmon coupling of gold nanorods at short distances and in different geometries. Nano Lett. 2009, 9, 1651–1658. [Google Scholar] [CrossRef] [PubMed]
- Pellas, V.; Hu, D.; Mazouzi, Y.; Mimoun, Y.; Blanchard, J.; Guibert, C.; Salmain, M.; Boujday, S. Gold Nanorods for LSPR Biosensing: Synthesis, Coating by Silica, and Bioanalytical Applications. Biosensors 2020, 10, 146. [Google Scholar] [CrossRef] [PubMed]
- Bossard-Giannesini, L.; Cruguel, H.; Lacaze, E.; Pluchery, O. Plasmonic properties of gold nanoparticles on silicon substrates: Understanding Fano-like spectra observed in reflection. Appl. Phys. Lett. 2016, 109, 111901. [Google Scholar] [CrossRef] [Green Version]
- Noblet, T.; Busson, B.; Humbert, C. Diagrammatic theory of linear and nonlinear optics for composite systems. Phys. Rev. A 2021, 104, 063504. [Google Scholar] [CrossRef]
- Dalstein, L.; Revel, A.; Humbert, C.; Busson, B. Nonlinear optical response of a gold surface in the visible range: A study by two-color sum-frequency generation spectroscopy. I. Experimental determination. J. Chem. Phys. 2018, 148. [Google Scholar] [CrossRef] [PubMed]
- Busson, B.; Dalstein, L. Nonlinear optical response of a gold surface in the visible range: A study by two-color sum-frequency generation spectroscopy. II. Model for metal nonlinear susceptibility. J. Chem. Phys. 2018, 149, 034701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Busson, B.; Dalstein, L. Nonlinear optical response of a gold surface in the visible range: A study by two-color sum-frequency generation spectroscopy. III. Simulations of the experimental SFG intensities. J. Chem. Phys. 2018, 149, 154701. [Google Scholar] [CrossRef] [PubMed]


| Visible Incidence Wavelength (nm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 480 | 500 | 523.5 | 540 | 550 | 560 | 580 | 600 | ||
| AuNPs | CNR | 1.4310 | 2.6538 | 2.3970 | 3.5530 | 4.8961 | 4.63128 | 4.0848 | 4.9943 |
| ΦNR (°) | 69.8753 | 59.4616 | 28.0546 | 12.6793 | 11.6879 | 5.5153 | 7.5741 | 4.6585 | |
| Vibr 1 | a1(a.u.) | −0.2376 | −1.8922 | −3.6383 | −9.5138 | −10.931 | −14.104 | −9.3308 | −12.517 |
| φ1 (°) | 0 | ||||||||
| ω1 (cm−1) | 1000 | ||||||||
| Γ1 (cm−1) | 3.5 | ||||||||
| 0.02757 | 0.5084 | 2.3039 | 7.17 | 4.9845 | 9.2743 | 5.2179 | 6.2813 | ||
| Vibr 2 | a2 (a.u.) | 0.5194 | 1.6344 | 5.2915 | 10.8236 | 16.4952 | 14.3315 | 10.3851 | 11.763 |
| φ2 (°) | 0 | ||||||||
| ω2 (cm−1) | 1023 | ||||||||
| Γ2 (cm−1) | 3.5 | ||||||||
| 0.1317 | 0.3793 | 4.8733 | 9.2801 | 11.3505 | 9.5759 | 6.4637 | 5.5474 | ||
| Vibr 3 (Mode 4 in [31,39]) | a3 (a.u.) | 0.2721 | 0.7215 | 2.6407 | 3 | 7.8051 | 5.2497 | 5 | 3 |
| φ3 (°) | 0 | ||||||||
| ω3 (cm−1) | 1071 | ||||||||
| Γ3 (cm−1) | 5 | ||||||||
| 0.0361 | 0.0739 | 1.2137 | 0.7129 | 2.5413 | 1.2849 | 1.4983 | 0.3608 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Humbert, C.; Pluchery, O.; Lacaze, E.; Busson, B.; Tadjeddine, A. Two-Colour Sum-Frequency Generation Spectroscopy Coupled to Plasmonics with the CLIO Free Electron Laser. Photonics 2022, 9, 55. https://doi.org/10.3390/photonics9020055
Humbert C, Pluchery O, Lacaze E, Busson B, Tadjeddine A. Two-Colour Sum-Frequency Generation Spectroscopy Coupled to Plasmonics with the CLIO Free Electron Laser. Photonics. 2022; 9(2):55. https://doi.org/10.3390/photonics9020055
Chicago/Turabian StyleHumbert, Christophe, Olivier Pluchery, Emmanuelle Lacaze, Bertrand Busson, and Abderrahmane Tadjeddine. 2022. "Two-Colour Sum-Frequency Generation Spectroscopy Coupled to Plasmonics with the CLIO Free Electron Laser" Photonics 9, no. 2: 55. https://doi.org/10.3390/photonics9020055
APA StyleHumbert, C., Pluchery, O., Lacaze, E., Busson, B., & Tadjeddine, A. (2022). Two-Colour Sum-Frequency Generation Spectroscopy Coupled to Plasmonics with the CLIO Free Electron Laser. Photonics, 9(2), 55. https://doi.org/10.3390/photonics9020055






