Active Optics—Advances of Cycloid-like Variable Curvature Mirrors for the VLTI Array
Abstract
:1. Introduction
- for the ESO-VLTI high-angular resolution astronomy, as the cat’s-eye mirrors of delay lines beam the recombination of the four 8-m telescopes (UT) and four 1.8-m telescopes (AT)—8 VCMs—as the extended-field-of-view system, and as the mirror-pair system. The AT x–y positions require output pupil conjugations of an observed object and a reference star—8 VCMs—for the central lab input pupil. The field-of-view considerations of the Paranal VLTI array were initiated by Beckers [9,10], and its development by von der Luehe et al. [11] and Glindemann et al. [12]. In addition to the on-axis cophasing by delay-lines, cat’s eye mirrors, i.e., VCMs realizing the cophasing of the field of view up to 3 arcsec. Dérie et al. [13], Koehler [14], and Gonté et al. [15] developed the delay-line telescope systems with the implementation of 16 VCMs.
2. Thin Circular Plate VCMs and Small Deformation Theory
2.1. VCM of Constant Thickness Distribution—CTD
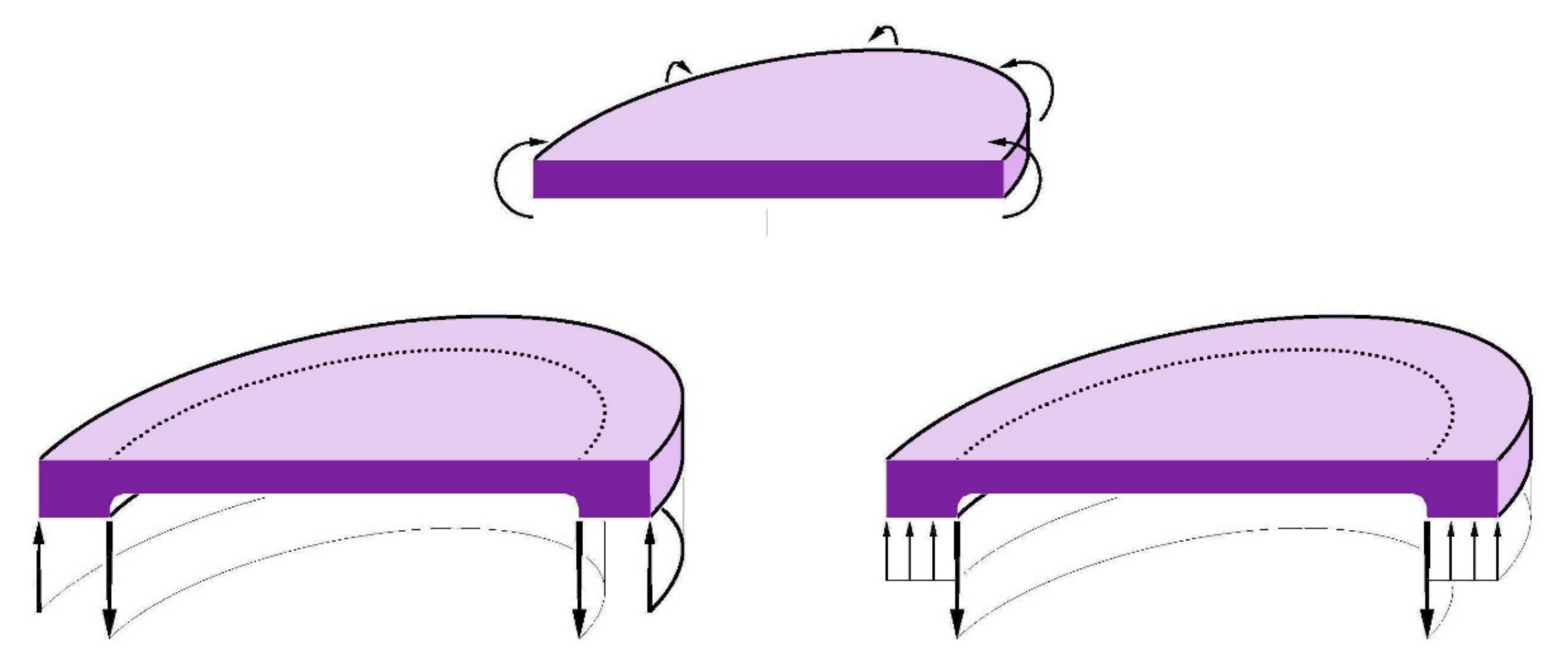
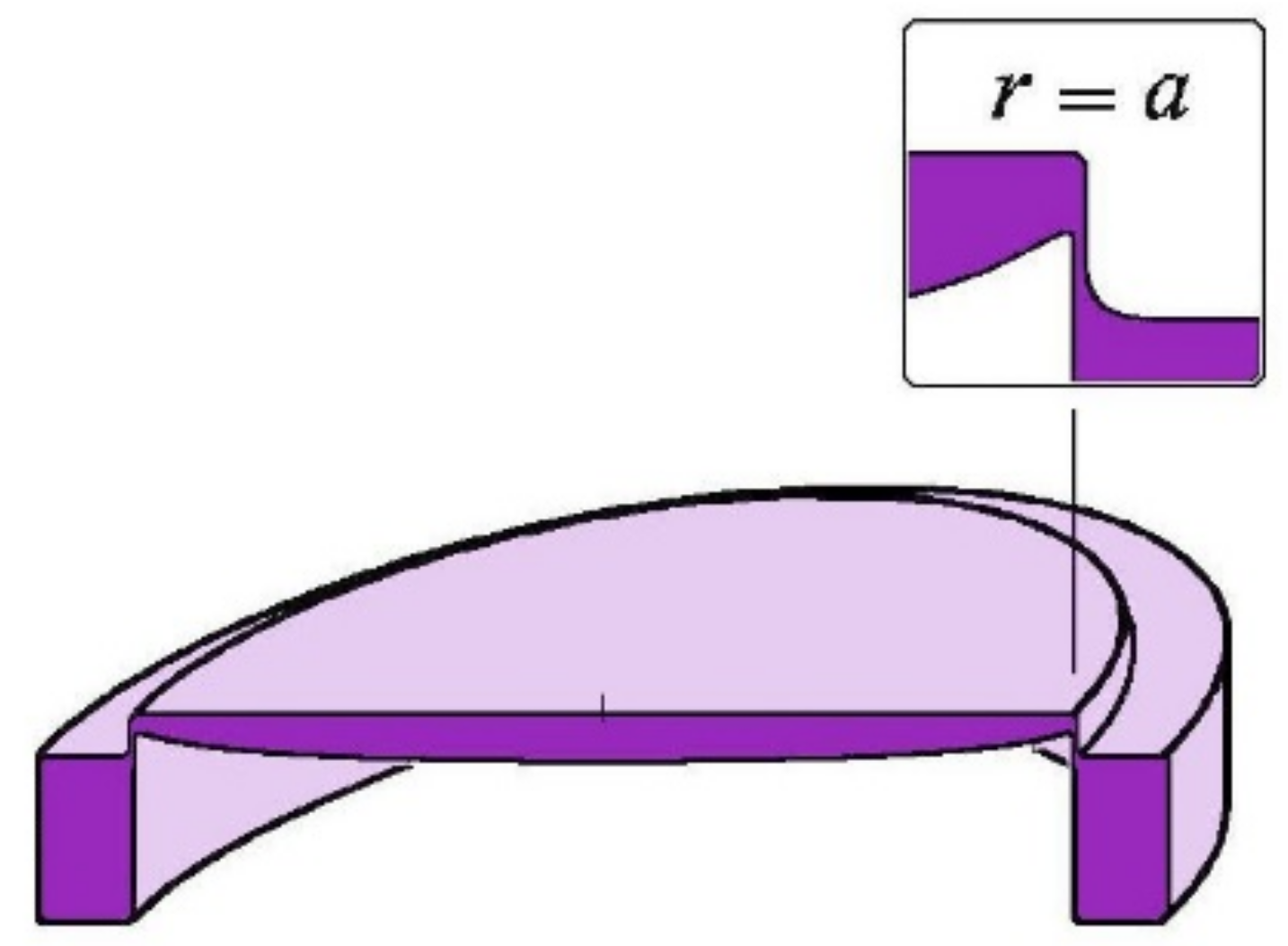
2.2. Plates of Variable Thickness Distribution—VTD—Cycloid-like Form—Tulip-like Forms
- VTD Type 1—Uniform loading and reaction at edge:
- VTD Type 2—Axial force at center and reaction at edge:
- VTD Type 3—Uniform loading and reaction at center:
3. Optical Focal-Ratio—Buckling Instability—VCM Zoom Range—Metal Choice
- Optical f-ratio: Whatever one of three VTD classes, we can determine an optical f-ratio generated by the Cv-1 deformation mode of a VCM. Assuming a flat mirror when in an unstressed state, let us define this f-ratio as Ω. Considering an aperture diameter 2a,
- Buckling instability: A self-buckling instability may happen during a curvature change. This is similarly to the meniscus shell “jumping toy”, in polymer material, which is manually brought, temporarily, to the opposite curvature. Avoiding buckling instability requires taking into account the radial tension, Nr, existing at the middle surface and showing that the maximum compression value of Nr remains small compared to a critical value.
- VCM zoom range: In order to avoid self-buckling instability, it is useful to consider a basic alternative where a VCM is polished flat when unstressed, and define a zoom range where all curvatures 1/Ri remain of the same algebraic sign when stressed.
- Metal choice: We selected VCM substrates in a quenched chromium stainless steel alloy Fe67Cr13, with post-quenched ageing that shows a large elastic deformability, much superior to that of fused silica or glass-ceramics. Deformability is characterized by the ratio of maximum working stress over the Young’s modulus, i.e., the σM.W.S/E ratio.
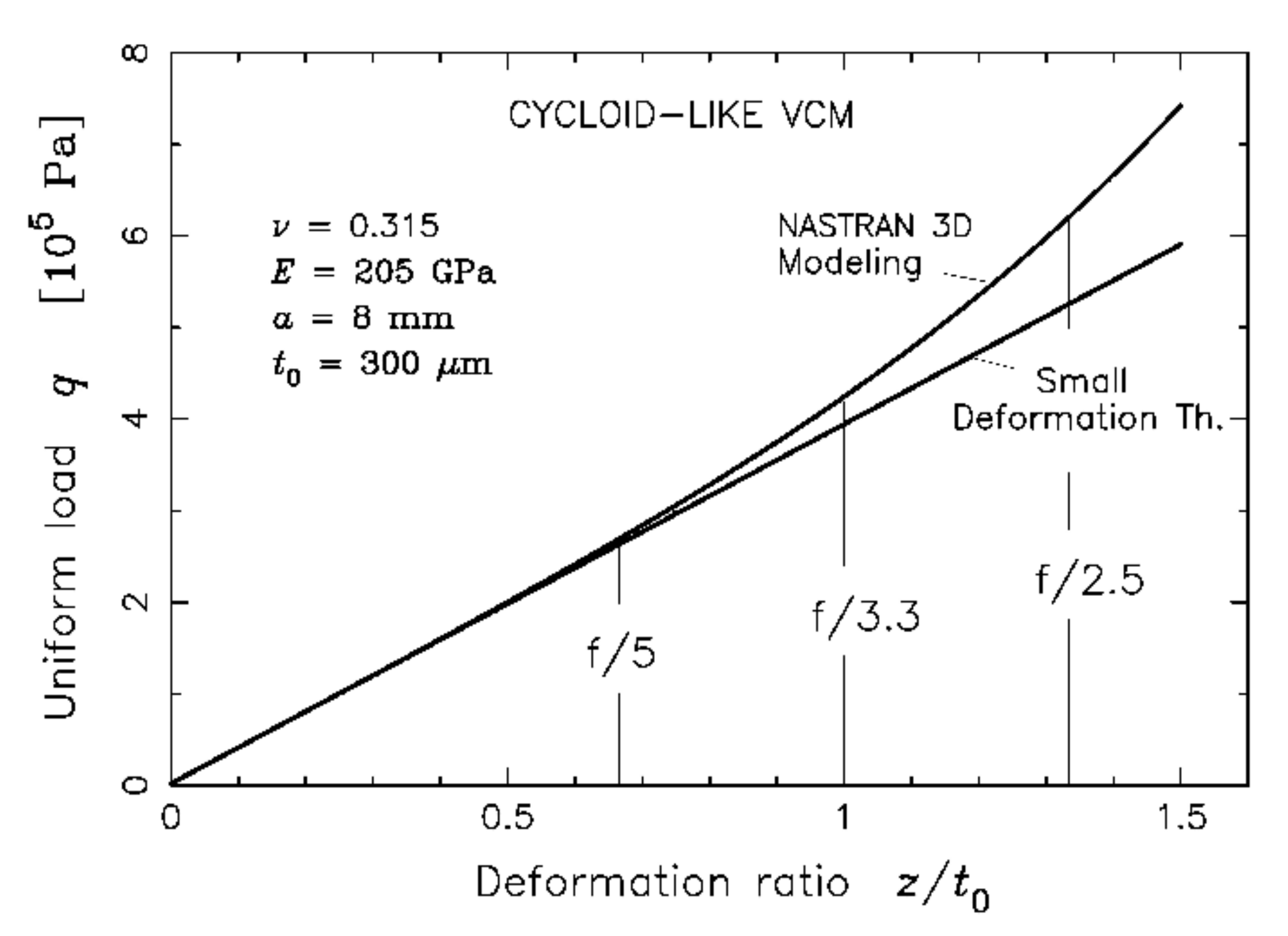
4. Cycloid-like VCM Modeling and Finite Element Analysis
4.1. VCM Modeling of a VTD Plate Alone under Uniform Load
4.2. VCM Modeling Linked to an Outer Cylinder Collarette and Rigid Ring
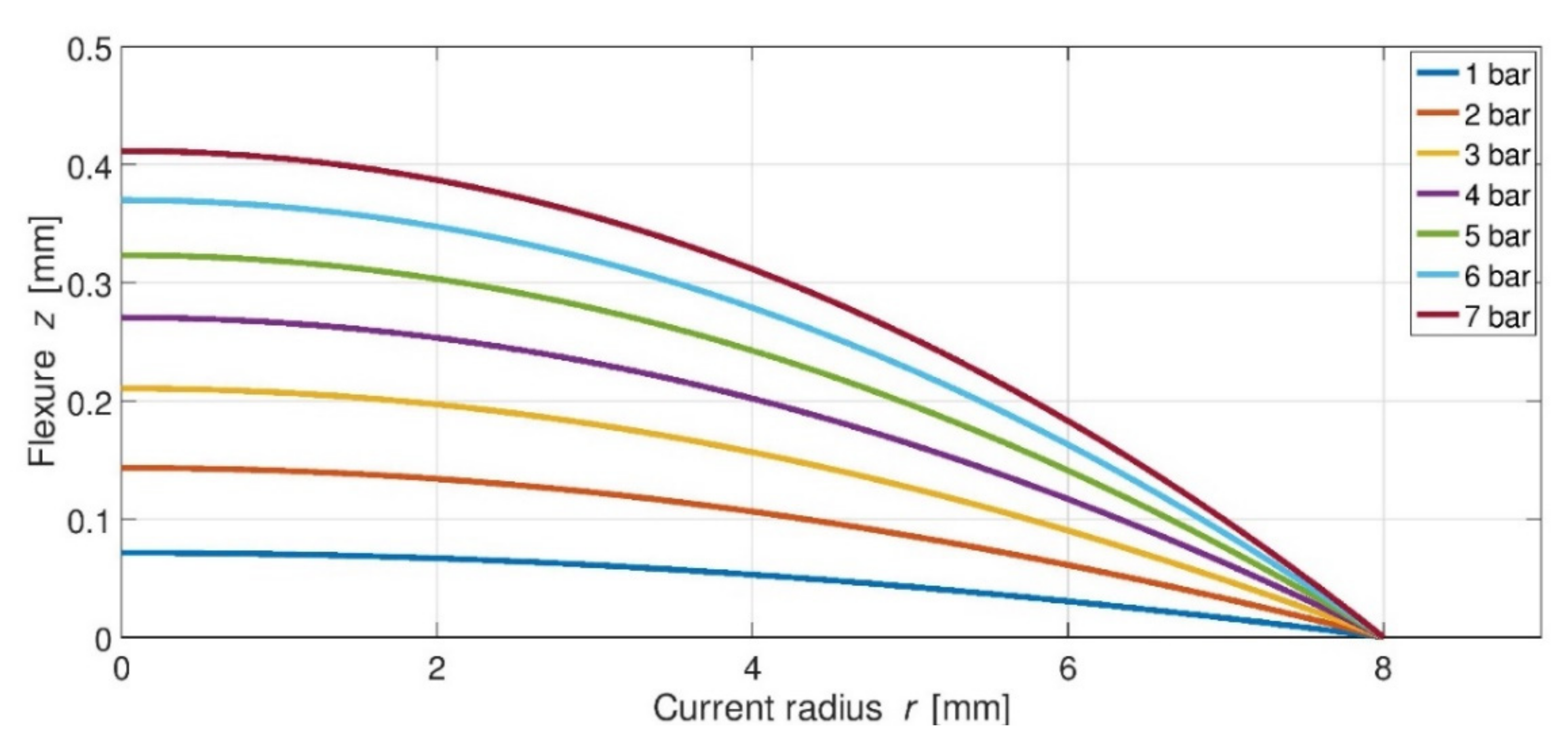
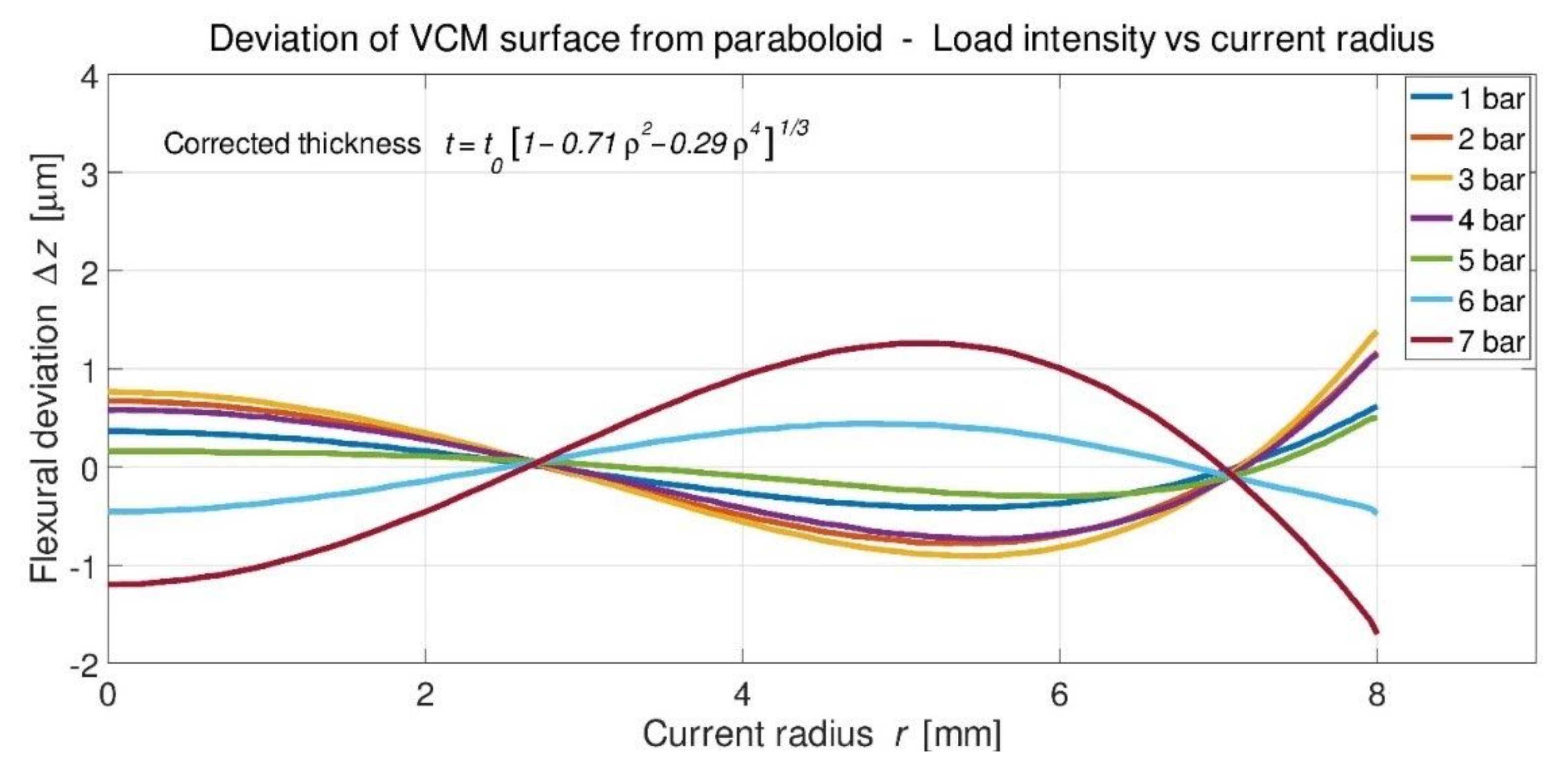
5. Realizations and Results of Cycloid-like VCMs
5.1. Various Developments with VCMs
5.2. VCM Material and Construction Process
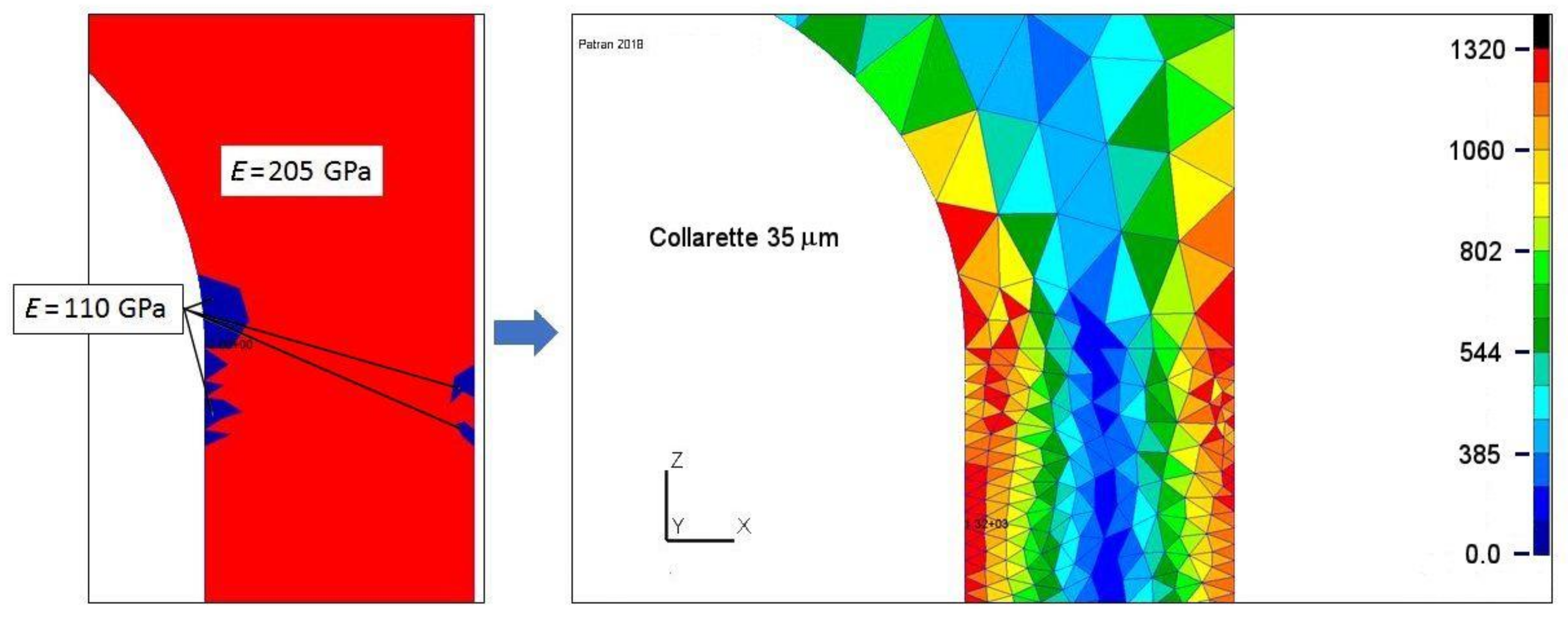
| Poisson ratio | ν = 0.315 | Young modulus | E = 205 GPa |
| Central thickness | t0 = 300 µm | Collarette radial thick. | ∆r = 30 μm |
| Optimized load | q = 5.3 daN·cm−2 | Collarette stress | σmax = 1100 MPa |
| Optimized flex.-sag | z0 = 298 µm | Radius of Curvature | R = 107.4 mm |
| Outer diameter | 2a = 16 mm | Zoom f-ratio | f/∞–f/3.35 |
| Clear aperture | dOpt = 13 mm | Zoom f-ratio | f/∞–f/4.14 |
| Maximum load | q = 6.0 daN·cm−2 | Max. zoom range for dOpt | f/∞–f/3.57 |
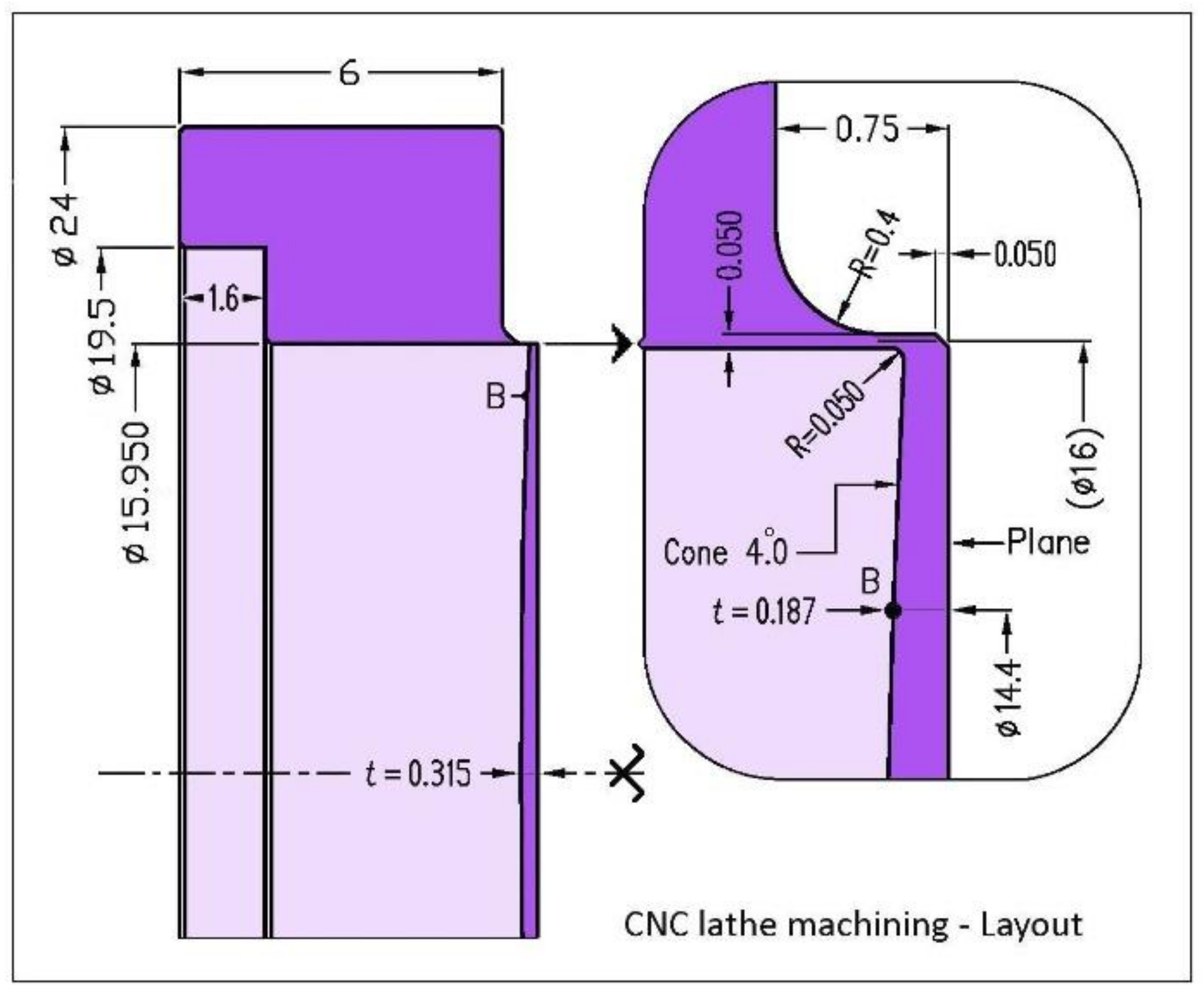
- Multi-function CNC machining with Hardinge lathe and polycrystalline cubic boron nitride (CBN) cutting tools [19]. A constant axial over-thickness is added for the machining, tCNC = 15 + t0 = 315-µm (Figure 18), giving room for the next grinding and polishing. The outer collarette radial thickness is machined slightly thicker, at ∆r = 50-µm. CNC positioning control accuracy is better than 1-µm (sub-contracted by Gauthier Precision SAS). However, the minimum chip thickness for a quenched chromium steel is close to, say, 10-μm. There exists a minimum chip cut thickness, below which no chip can be formed stably, as shown in Matsumura [20].
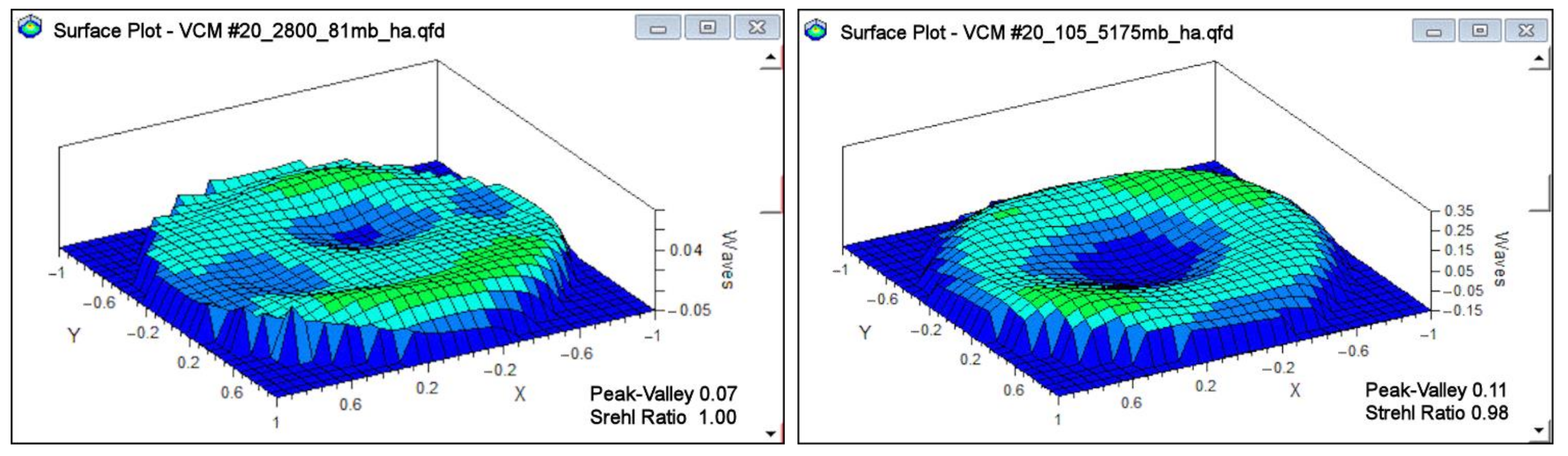
- Front surface grinding, 3-µm diamond grain, with, preferably, a flat cast-iron tool—or a concave tool with up to 10-µm sag—ensuring the minimum curvature matter removal from the previous lathe surface. Fizeau checking at caliber R2800.
- Rear face edge grinding, 3-µm diamond grain, with an appropriate conical form in cast iron. The VCM, rear side up, rotating slowly, and the conical form rotating from slow to increasing speed.
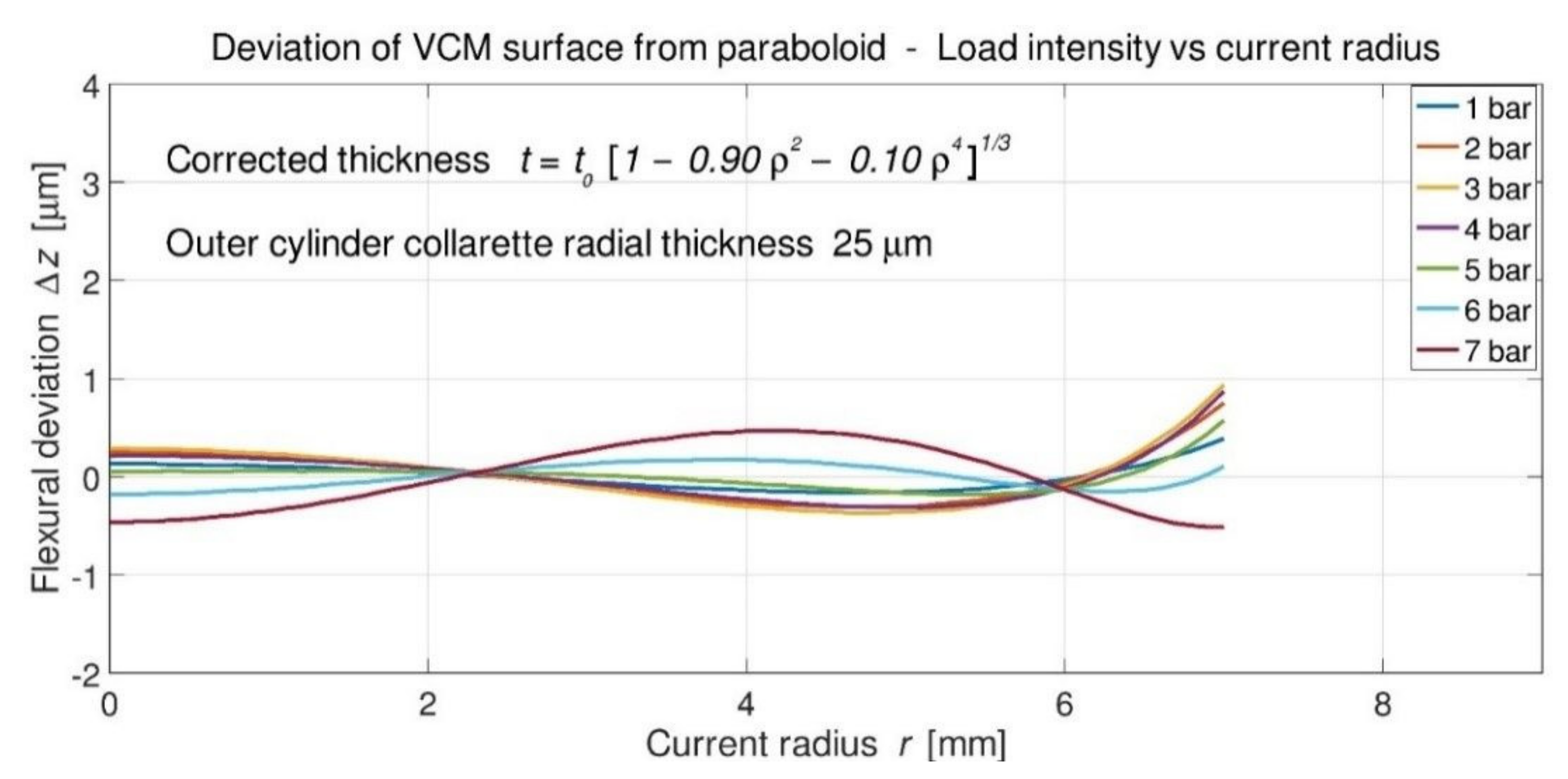
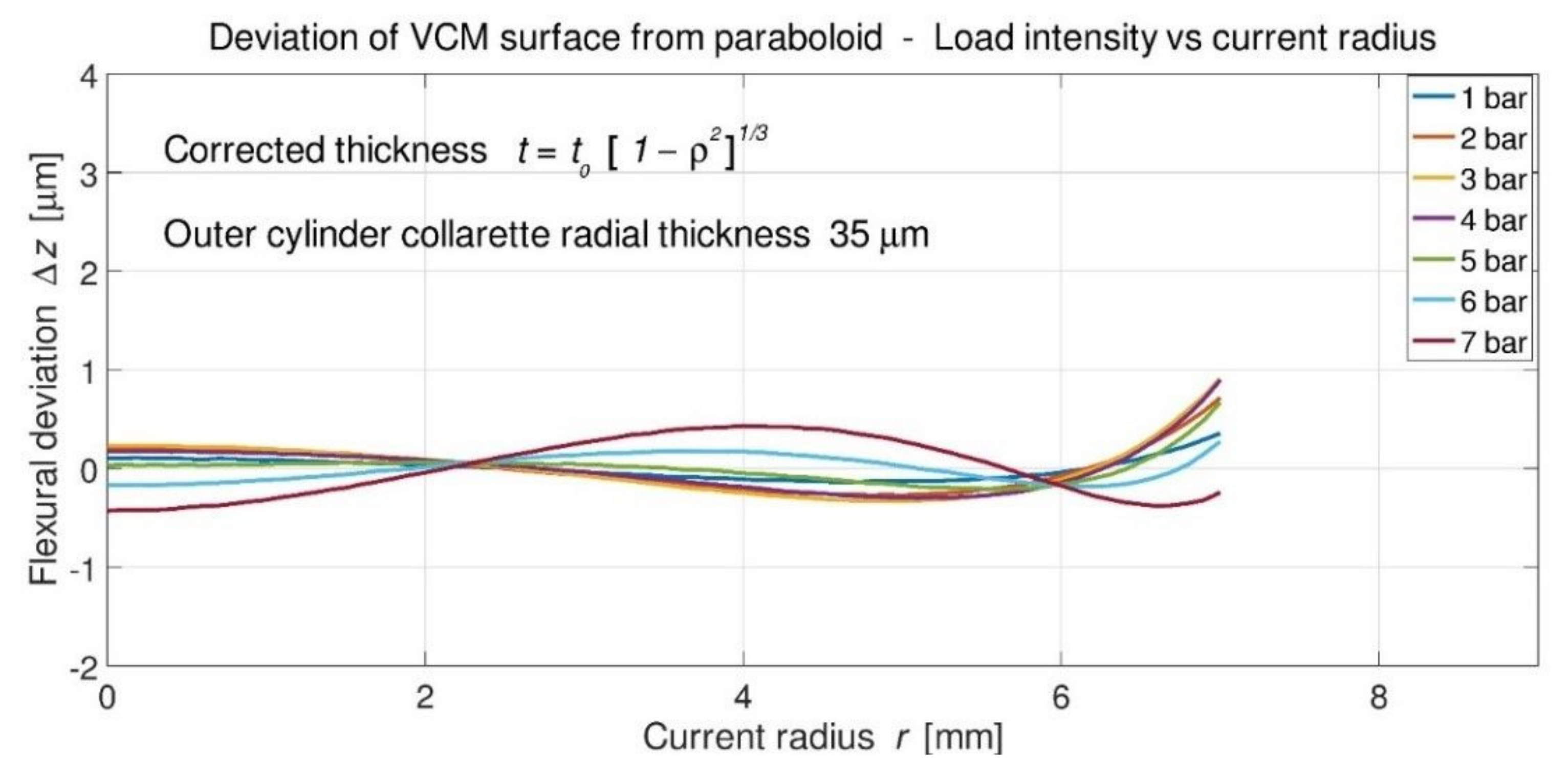
- Outer edge collarette rectification of VCM mounted on lab lathe with a flexible clamp rotating slowly—centering better than 0.2-µm accuracy. Machining at a 10° inclination, with a small external grinding wheel in cubic boron nitride (CBN) at 18,000-rpm. The collarette radial thickness becomes ∆r ≅ 30 to 35-µm.
- Repeat stage 2 of front surface grinding. Use an optimal concave tool among 0, 2, 4, 6, 8, 10, 12-µm sags for minimum removal matter. Fringe Fizeau checking at caliber R2800.
- Pre-stressing at the maximal load between 5 and 5.5-bars to slightly overpass R105 Fizeau test. This generates a convexity of 9-µm sag, typically, over a 14-mm diameter in the Fizeau test R2800. This convexity is due to the collarette high stress which also generates an axial displacement of ~8-µm, typically, i.e. its axial elongation. Pre-stressing provides elasticity linearization of the stress–strain relation at the collerette level (see Section 5.3).
- Repeat grinding of stage 5 of the front surface grinding. Use the optimal concave tool for minimum removal matter. Fizeau checking at R2800. N.B.: If the VCM convexity overpasses 17-µm sag, then one operates directly to stage 8 of the operation.
- Inverse stressing if necessary. The curvature of caliber R2800, with respect to a plane surface, corresponds to a sag of 8.7-µm. If the convexity is in the range sag 17-22-µm—and since the collerette plastic effect is due to dominant stresses in the pre-stressing operation between 5 and 5.5-bars—, then one requires a special loading device. This device can generate an air pressure loading at the VCM’s opposite side, by successive trials up to 8-bars as a maximum. After this operation, one makes the pre-stressing again, as in stage 6, for reshaping. Repeat this operation up to obtaining a curvature of 17-µm sag at R2800 Fizeau checking. A cycle inverse stressing and pre-stressing is able to reduce convexity up to a 5-µm sag amount without removing material. If this result is not achieved, the VCM’s substrate is discarded.
- Polishing with a pitch tool rotating below, by Lanzoni. The VCM translates up the tool. Alumina abrasive Al2O3, grain size 1-µm for 8–12 h, 0.3-µm for 8–12 h, and 0.05-µm for 1 h. Polishing pressure is 30-g.cm−2. The polishing cinematic parameters generate either concavity or maintain a stable curvature. Then, starting from a VCM convexity smaller than 17-µm sag, a slightly convex 6-µm sag shape is achieved at the end of polishing. Fizeau checking at R2800.
- He-Ne interferogram data acquisitioned by Lanzoni with the Fizeau test with calibers from R2800 to R105.
- Gold coating in the vacuum chamber for near-infrared and infrared by ESO.
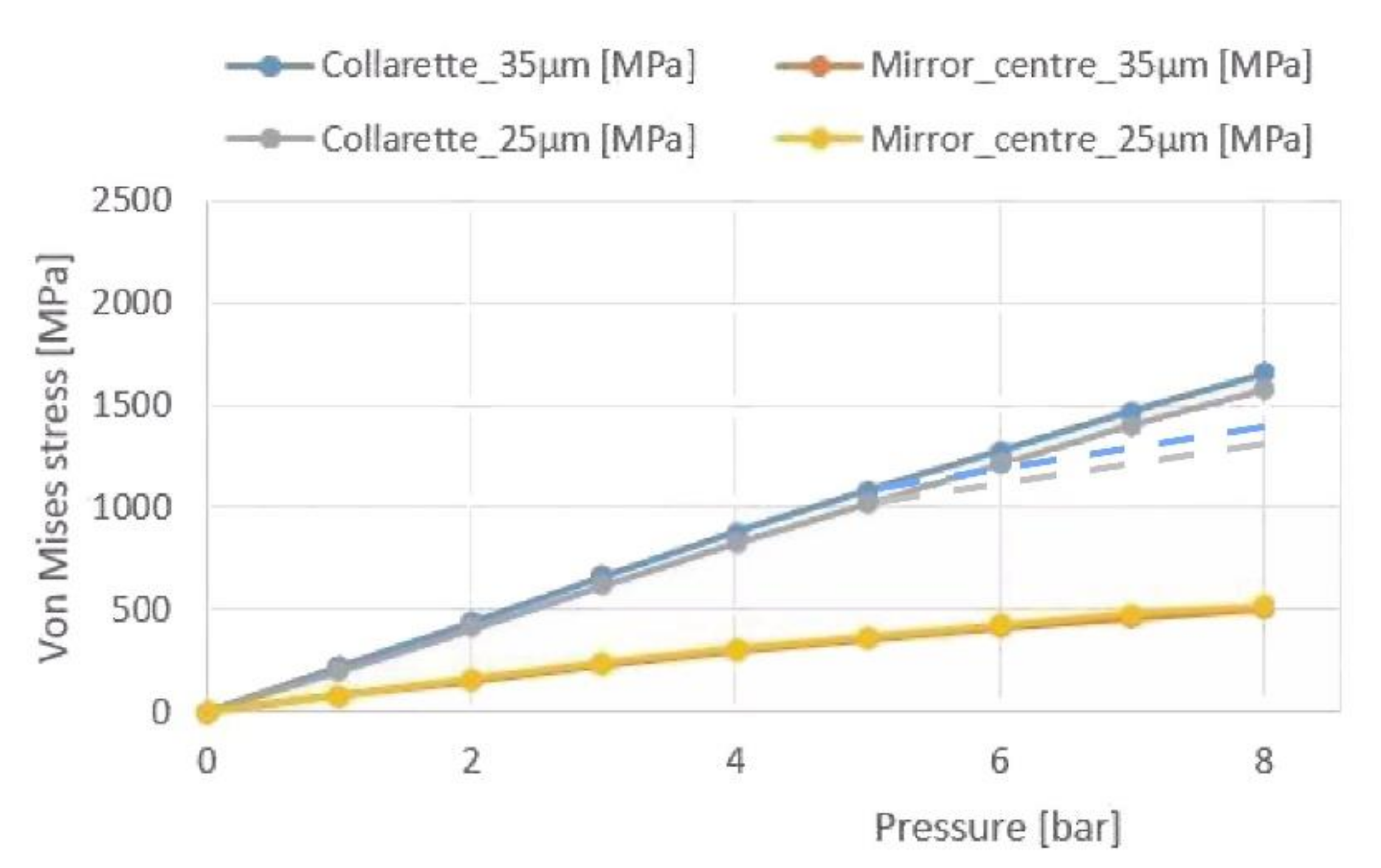
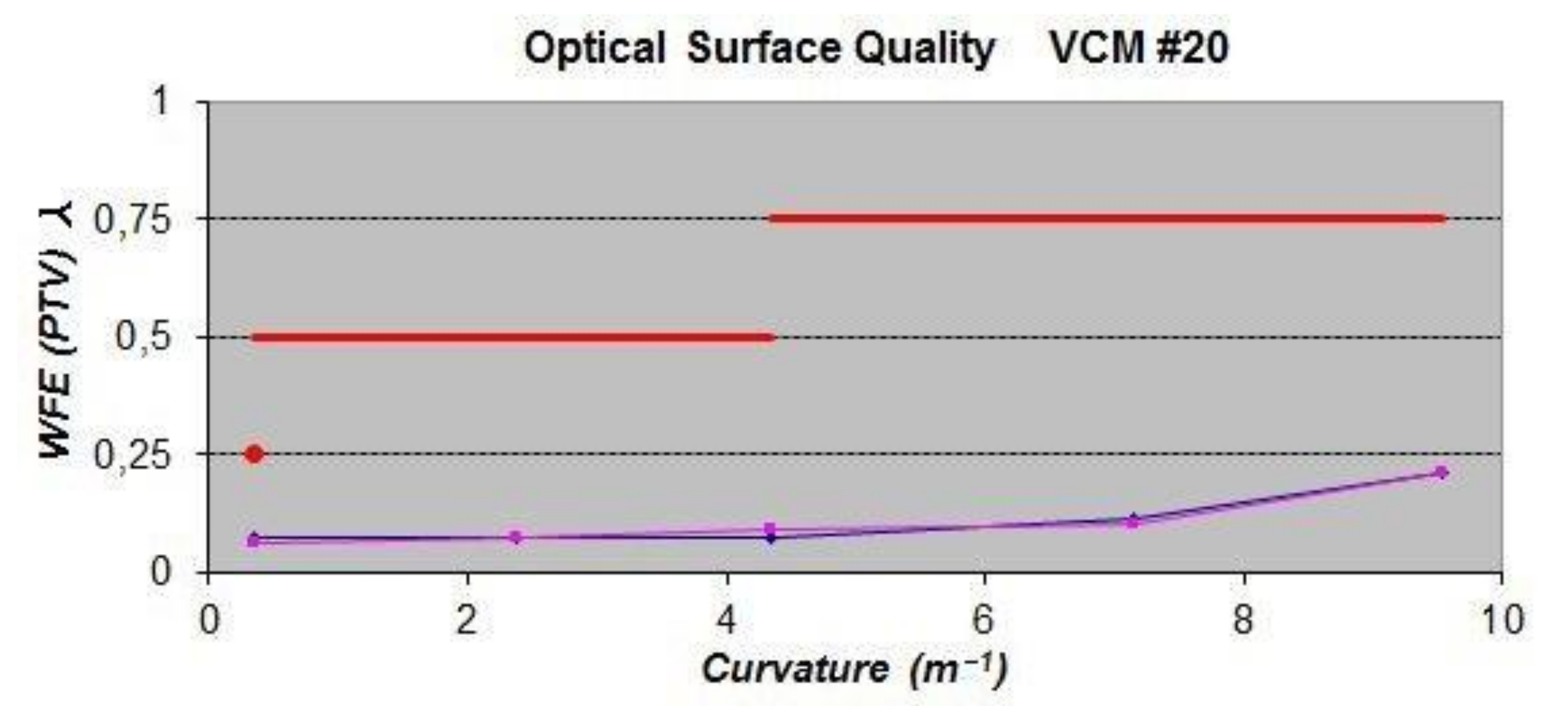
5.3. Pre-Stressing and Maximum Stresses
5.4. Deformability Advantage of Present Alloy over Some Other Materials
5.5. Interferometric Results
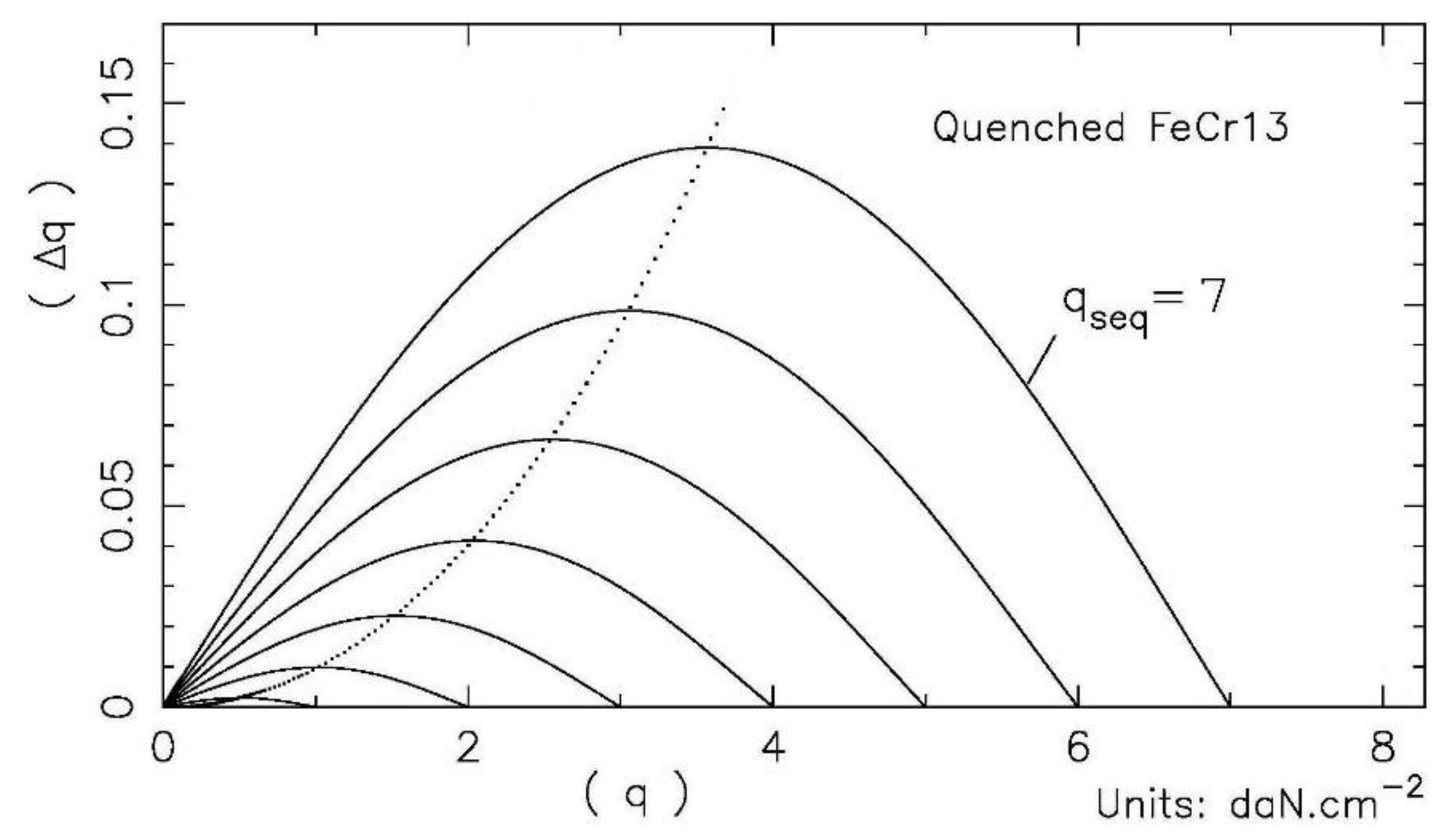
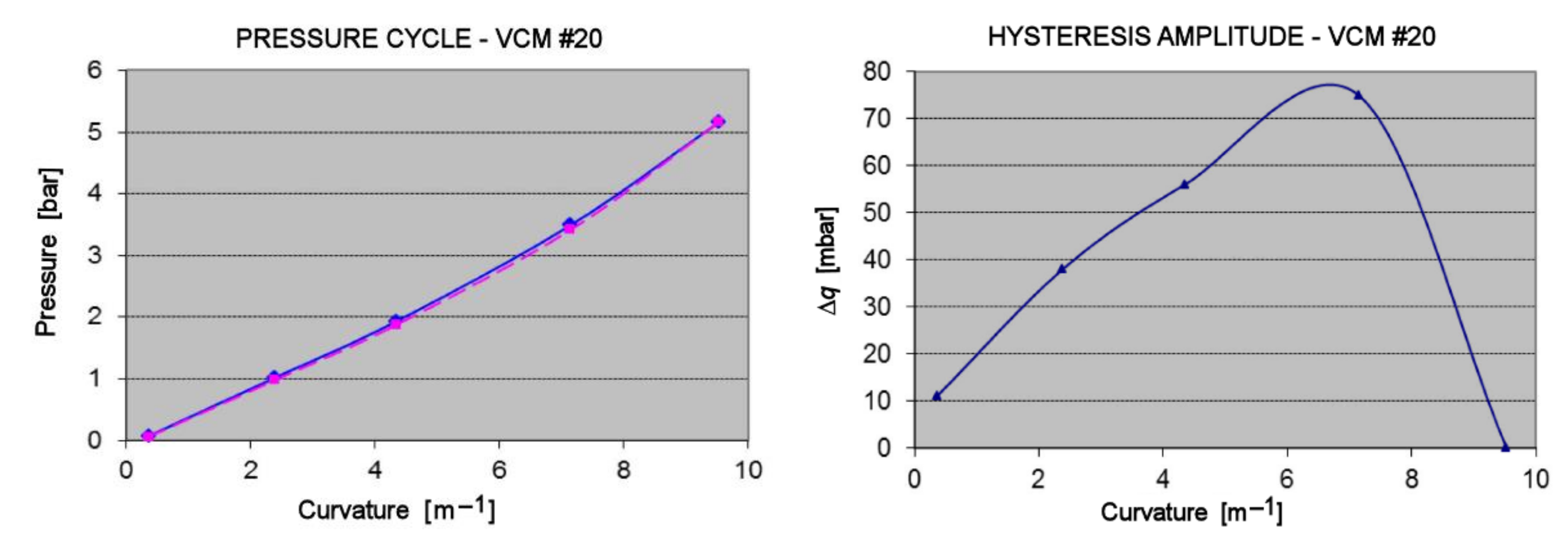
5.6. Hysteresis Cycles and Hysteresis Modeling
- During the de-loading, the same curvatures than when loading are obtained by lower applied loads.
- After the loading and subsequent de-loading sequence of about 12 h, the initial and final curvatures are identical in a new cycle.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lemaitre, G.R. Elasticité et Miroirs à Focale Variable. Comptes Rendus De L’Académie Sci. 1976, 282, 87. [Google Scholar]
- Ferrari, M.; Lemaitre, G.R. Analysis of large deflection zoom mirrors for the ESO VLTI. Astron. Astrophys. 1993, 274, 12–18. [Google Scholar]
- Ferrari, M. Development of variable curvature mirrors for the delay lines of the VLTI. Astron. Astrophys. Suppl. Ser. 1998, 128, 221–227. [Google Scholar] [CrossRef] [Green Version]
- Lemaitre, G.R. Elasticity Theory and Astronomical Optics—Active Optics Methods; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-68905-8. [Google Scholar]
- Connes, P. Astronomical Fourier spectroscopy. Annu. Rev. Astron. Astrophys. 1970, 8, 209–230. [Google Scholar] [CrossRef]
- Camy-Peyret, C.; Payan, S.; Jeseck, P.; Té, Y. Mesures spectroscopiques de constituents. Comptes Rendus De L’académie Sci. Ser. IV-Phys. 2001, 2, 905–922. [Google Scholar]
- Labeyrie, A. Stellar interferometry methods. Ann. Rev. Astron. Astrophys. 1978, 16, 77–102. [Google Scholar] [CrossRef]
- Mourard, D.; Bonneau, D.; Glentzlin, A.; Merlin, G.; Petrov, R.G.; Pierron, M.; Thureau, N.D.; Abe, L.; Berio, P.; Blazit, A. The GI2T/REGAIN interferometer, in Astronomical Interferometry. In Proceedings of the Astronomical Telescopes and Instrumentation, Munich, Germany, 27 March–1 April 2000. [Google Scholar] [CrossRef]
- Beckers, J.M. Field of view considerations for telescope arrays. In Proceedings of the 1986 Astronomy Conferences, Tucson, AZ, USA, 1–2 March 1986. [Google Scholar]
- Beckers, J.M. Interferometric imaging with the VLTI. J. Opt. 1991, 22, 73. [Google Scholar] [CrossRef]
- von der Luehe, O.; Derie, F.; Koehler, B.; Leveque, S.A.; Paresce, F.; Verola, M. Interferometry with the ESO very large telescope. In Optical Telescopes of Today and Tomorrow; International Society for Optics and Photonics: Landskrona/Hven, Sweden, 1997; Volume 2871, pp. 498–503. [Google Scholar] [CrossRef]
- Glindemann, A.; Abuter, R.; Carbognani, F.; Delplancke, F.; Derie, F.; Gennai, A.; Gitton, P.B.; Kervella, P.; Koehler, B.; Leveque, S.A. The VLT Interferometer: A unique instrument for high-resolution astronomy. In Interferometry in Optical Astronomy; International Society for Optics and Photonics: Munich, Germany, 2000; Volume 4006, pp. 2–12. [Google Scholar] [CrossRef]
- Dérie, F.J. VLTI delay lines: Design, development and performance requirements. In Interferometry in Optical Astronomy; International Society for Optics and Photonics: Munich, Germany, 2000; pp. 25–30. [Google Scholar] [CrossRef]
- Koehler, B.; Leveque, S.A.; Gitton, P.B. A decade of VLTI technical development. In Interferometry for Optical Astronomy II; International Society for Optics and Photonics: Waikoloa, HI, USA, 2003; Volume 4838. [Google Scholar] [CrossRef]
- Gonté, F.Y.J.; Alonso, J.; Aller-Carpentier, E.; Andolfato, L.; Berger, J.P.; Cortes, A.; Delplancke-Strobele, F.; Donaldson, R.; Dorn, R.J.; Dupuy, C. NAOMI: A low-order adaptive optics system for the VLT Interferometer. In Optical and Infrared Interferometry and Imaging V; International Society for Optics and Photonics: Edinburgh, UK, 2016; p. 990720. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill Publ. Company: New York, NY, USA, 1964; p. 396. ISBN1 10:0070858209. ISBN2 13:9780070858206. [Google Scholar]
- Connes, P.; Michel, G. Astronomical Fourier spectrometer. Appl. Opt 1974, 14, 2067–2084. [Google Scholar] [CrossRef] [PubMed]
- Ugitech Corp. UGIMA 4028W. 1990. Available online: https://eservices.ugitech.com/CatalogDocuments/BarProducts.pdf (accessed on 18 January 2022).
- Klimenko, S.A.; Mukovoz, Y.A.; Lyashko, V.A.; Vashchenko, A.N.; Ogorodnik, V.V. On the wear mechanism of cubic boron nitride base cutting tools. Wear 1992, 157, 1–7. [Google Scholar] [CrossRef]
- Matsumura, T. Chip formation and minimum chip thickness. In Comprehensive Materials Processing; Elsevier Ltd.: Amsterdam, The Netherlands, 2014; Section 11.07.4.1; ISBN 978-0-08-096533-8. [Google Scholar]
- Aubert & Duval Corp. Strength of Quenched Chromium Stainless Steel. 2000. Available online: https://www.aubertduval.com/wp-media/uploads/sites/2/pdf/fr_X13.pdf (accessed on 18 January 2022).
- Quick Fringes Code by Diffraction Limited Corp. Ottawa, Canada. Available online: https://diffractionlimited.com (accessed on 18 January 2022).
- Lemaitre, G.R.; Ferrari, M.; Mazzanti, S.P.; Lanzoni, P.; Joulie, P.; Leduc, D.; Copede, M. VLTI pupil transfer: Variable curvature mirrors II—Plasticity, hysteresis, and curvature control. In Interferometry in Optical Astronomy; International Society for Optics and Photonics: Munich, Germany, 2000; pp. 192–197. [Google Scholar] [CrossRef]




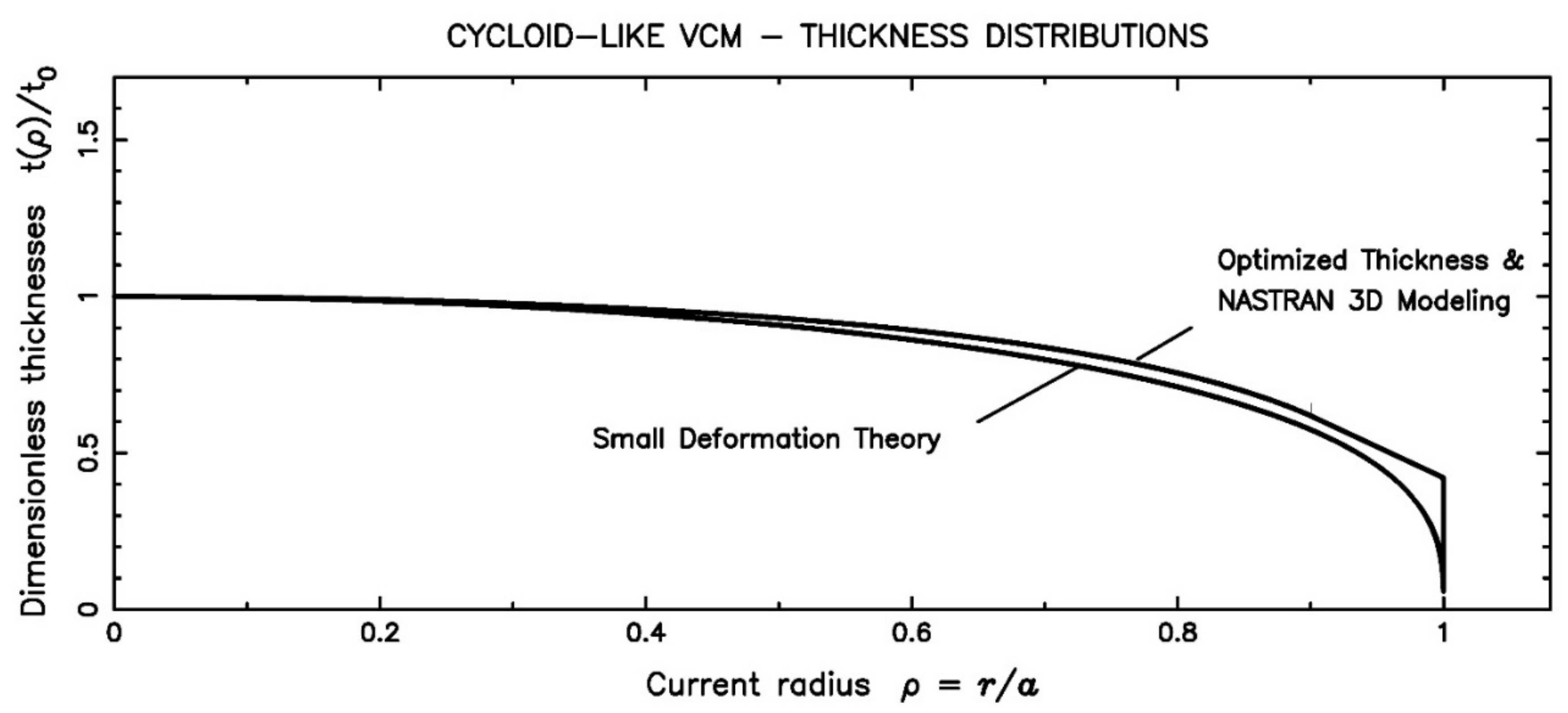
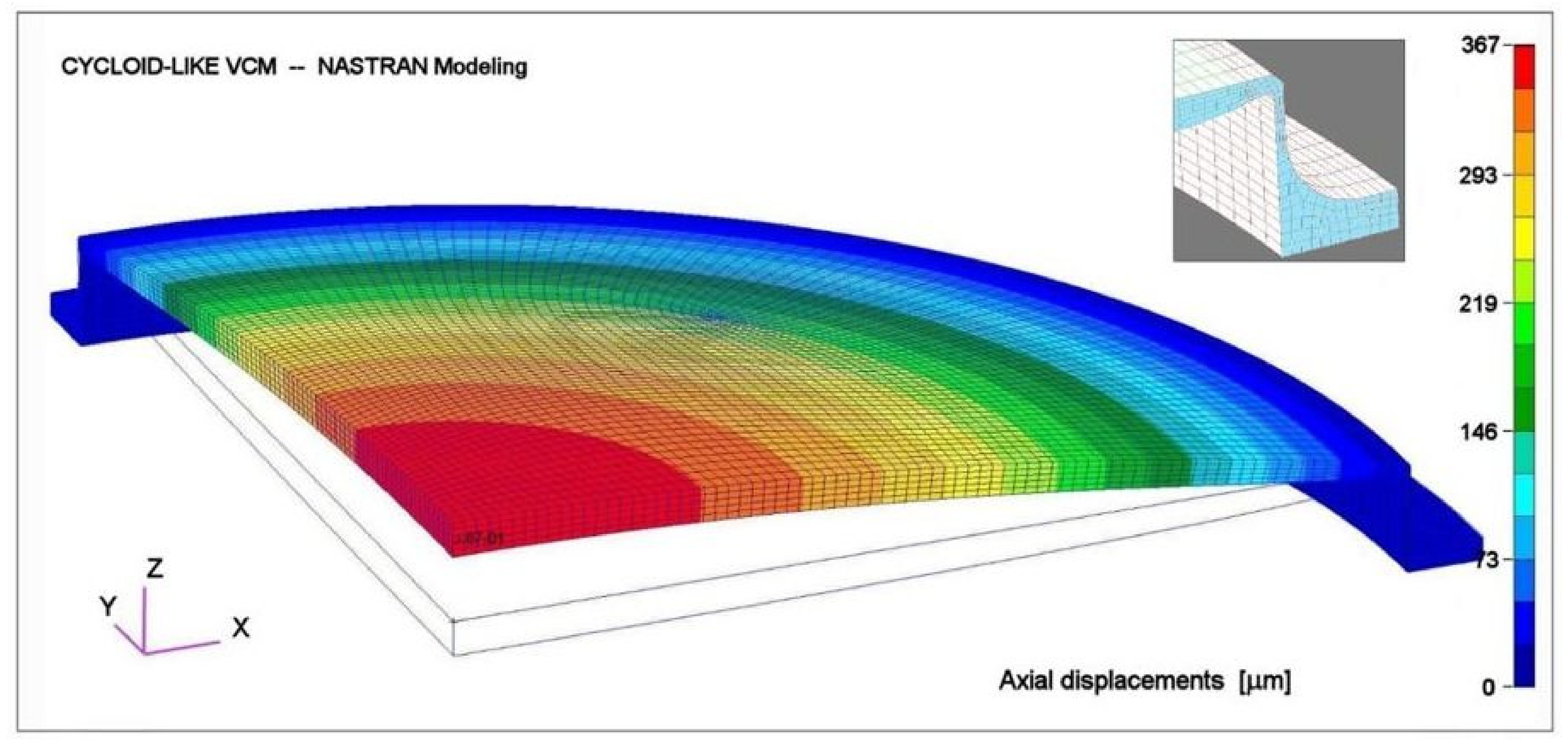








| Radius ρ | (1 − ρ2)1/3 | TNastran | Comment |
|---|---|---|---|
| 0.00 | 1.0000 | 1.0000 | |
| 0.20 | 0.9864 | 0.9864 | |
| 0.40 | 0.9435 | 0.9435 | |
| 0.50 | 0.9085 | 0.9085 | |
| 0.60 | 0.8618 | 0.8618 | |
| 0.70 | 0.7989 | 0.7989 | |
| 0.80 | 0.7114 | 0.7114 | |
| 0.90 | 0.5749 | 0.5749 | conical |
| 0.95 | 0.4602 | 0.4861 | conical |
| 0.99 | 0.2710 | 0.4150 | conical |
| 1.00 | 0.0000 | 0.3973 | conical |
| r (mm) | 0 | 2 | 4 | 5 | 6 | 7 | 7.2 | 8- | 8 | 8+ | 12 |
| t (µm) | 300 | 293 | 272 | 254 | 228 | 185 | 172 | 120 | 6750 | 6000 | 6000 |
| t* (µm) | 315 | 308 | 287 | 269 | 243 | 200 | 187 | 135 | 6750 | 6000 | 6000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lemaitre, G.R.; Vola, P.; Lanzoni, P.; Mazzanti, S.; Dérie, F.J.; Gonté, F.Y. Active Optics—Advances of Cycloid-like Variable Curvature Mirrors for the VLTI Array. Photonics 2022, 9, 66. https://doi.org/10.3390/photonics9020066
Lemaitre GR, Vola P, Lanzoni P, Mazzanti S, Dérie FJ, Gonté FY. Active Optics—Advances of Cycloid-like Variable Curvature Mirrors for the VLTI Array. Photonics. 2022; 9(2):66. https://doi.org/10.3390/photonics9020066
Chicago/Turabian StyleLemaitre, Gerard Rene, Pascal Vola, Patrick Lanzoni, Silvio Mazzanti, Frederic J. Dérie, and Frederic Y. Gonté. 2022. "Active Optics—Advances of Cycloid-like Variable Curvature Mirrors for the VLTI Array" Photonics 9, no. 2: 66. https://doi.org/10.3390/photonics9020066





