Machine Learning Based Low-Cost Optical Performance Monitoring in Mode Division Multiplexed Optical Networks
Abstract
:1. Introduction
2. Fmf Optical Channel
3. The Proposed OPM Scheme
3.1. Asynchronous Tap Delay Histogram (ADTH)
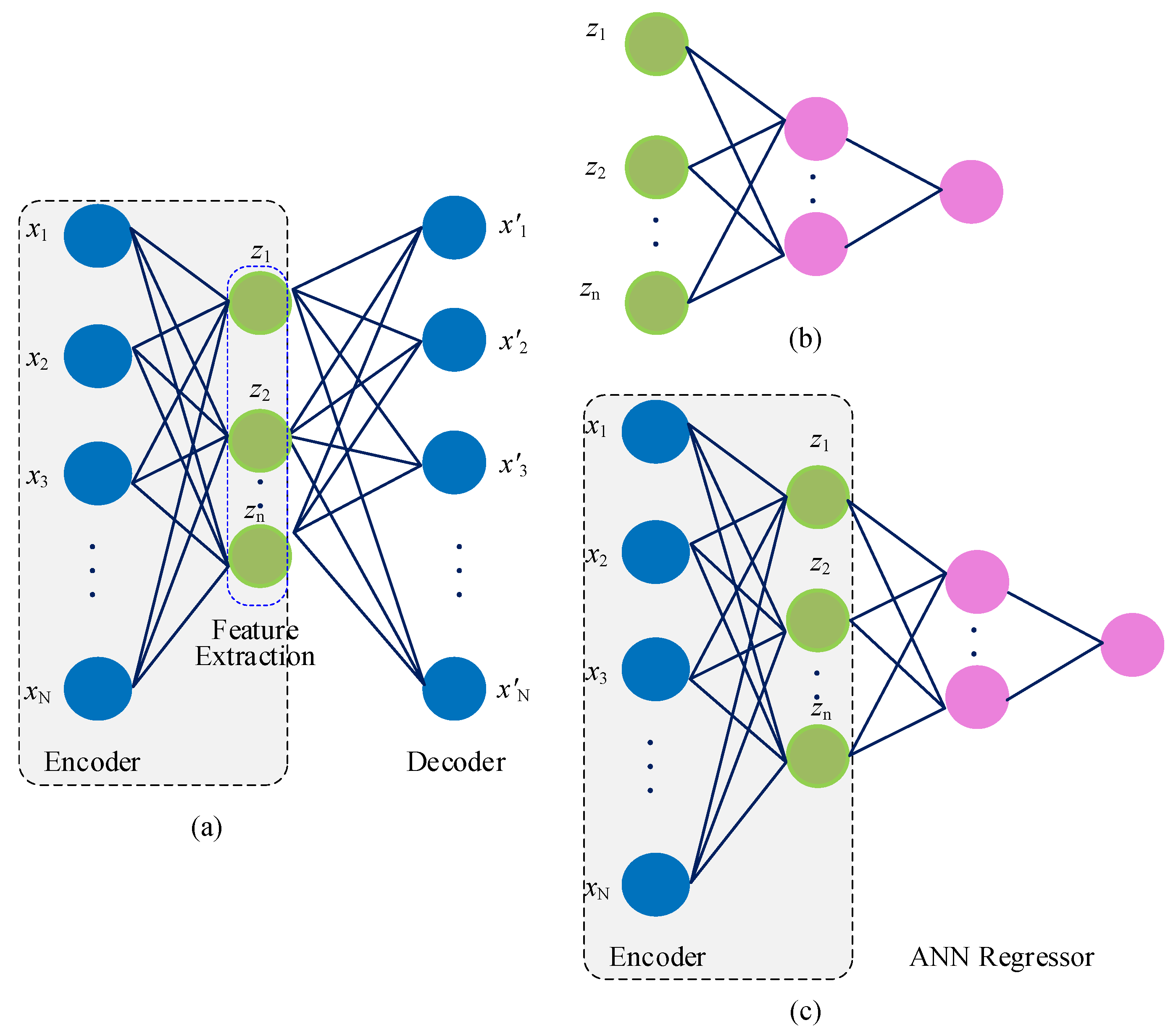
3.2. Opm Using ADTH with AE
- An encoder part which transfers the input vector x to a feature vector z.
- A decoder part that uses the feature vector z to reconstruct the input vector x.
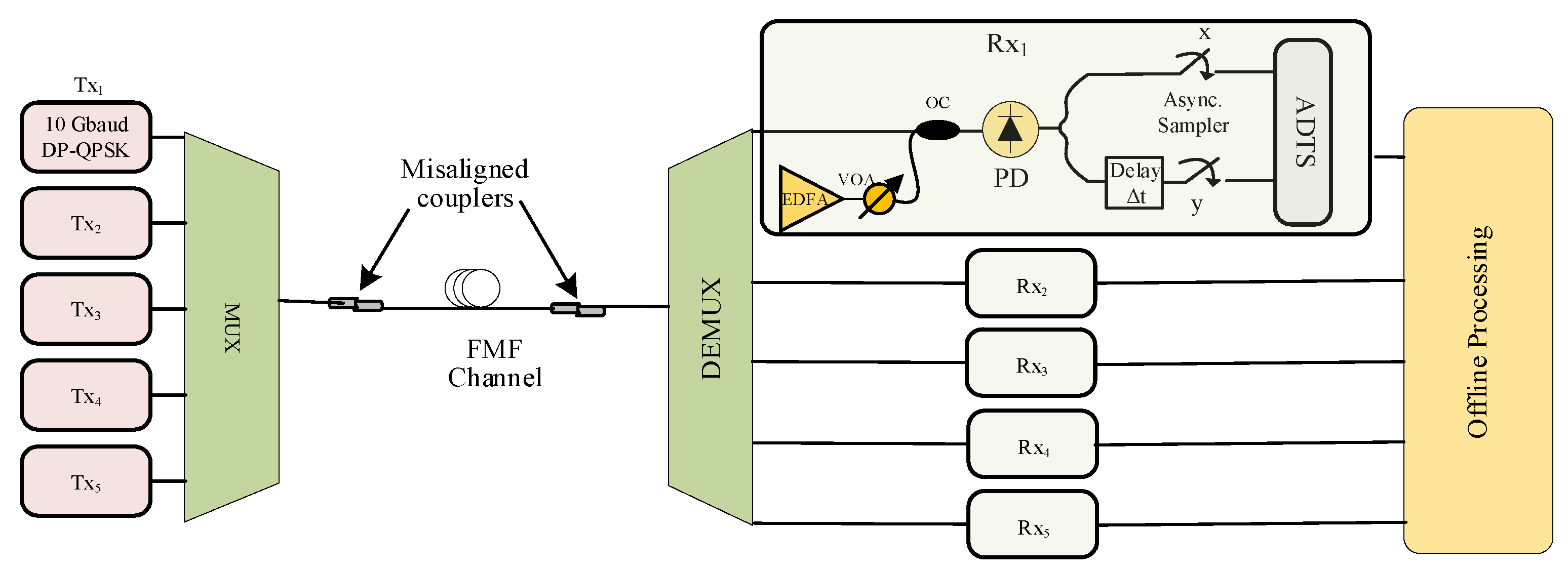
4. Simulation Setup
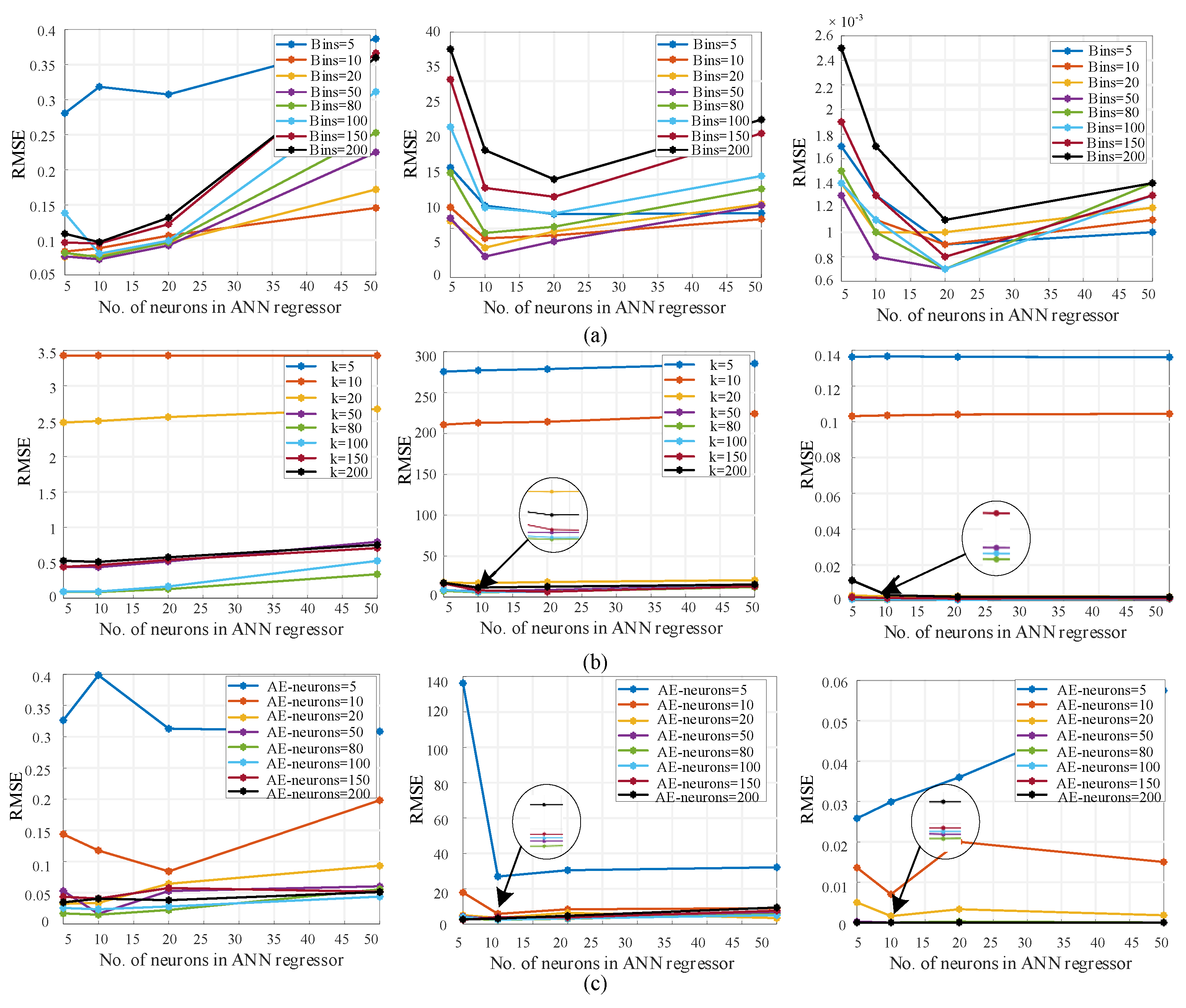
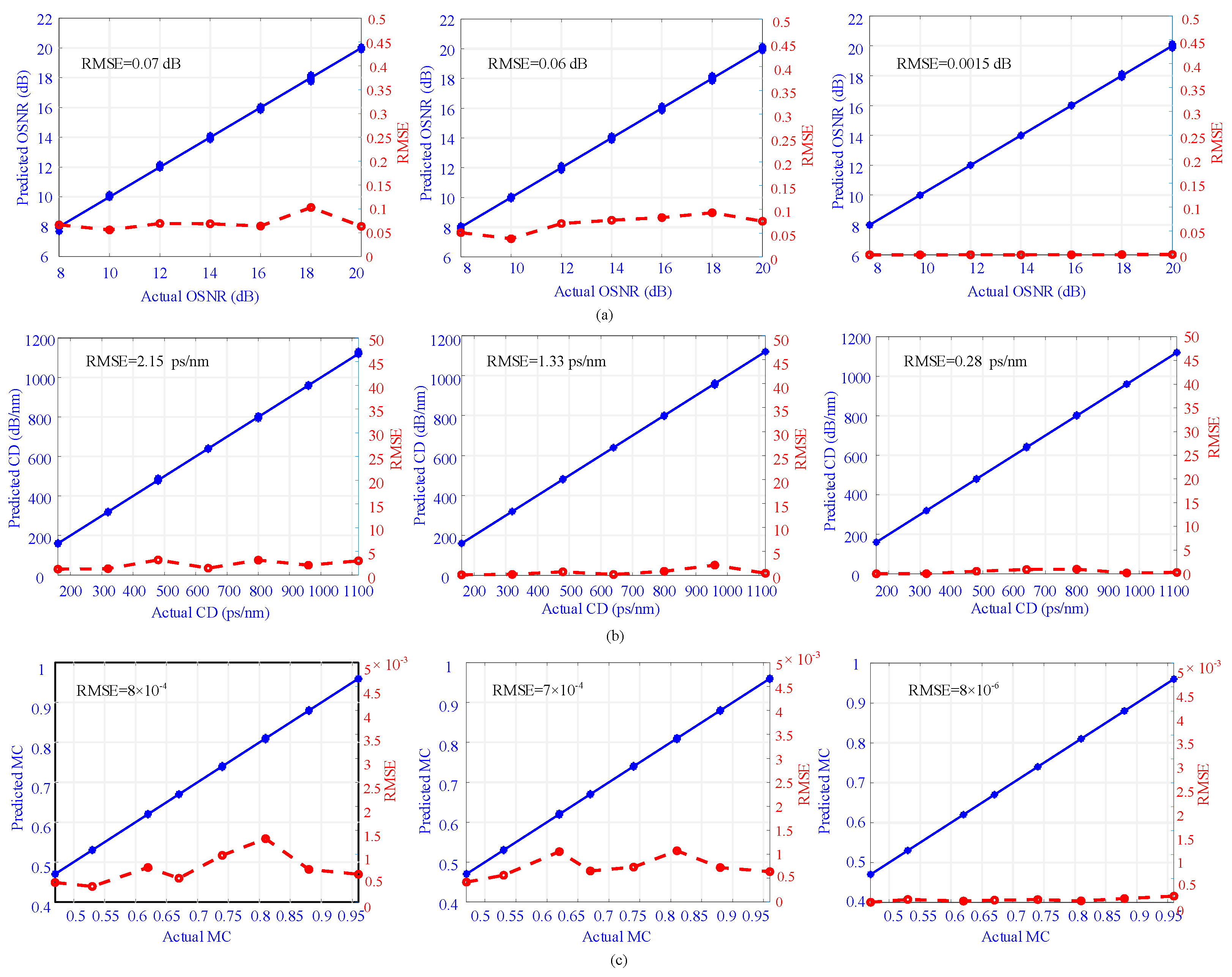
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saridis, G.M.; Alexandropoulos, D.; Zervas, G.; Simeonidou, D. Survey and evaluation of space division multiplexing: From technologies to optical networks. IEEE Commun. Surv. Tutor. 2015, 17, 2136–2156. [Google Scholar] [CrossRef] [Green Version]
- Essiambre, R.J.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity limits of optical fiber networks. J. Lightwave Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Gerstel, O.; Jinno, M.; Lord, A.; Yoo, S.B. Elastic optical networking: A new dawn for the optical layer? IEEE Commun. Mag. 2012, 50, s12–s20. [Google Scholar] [CrossRef]
- Jinno, M.; Ohara, T.; Sone, Y.; Hirano, A.; Ishida, O.; Tomizawa, M. Elastic and adaptive optical networks: Possible adoption scenarios and future standardization aspects. IEEE Commun. Mag. 2011, 49, 164–172. [Google Scholar] [CrossRef]
- Chatterjee, B.C.; Sarma, N.; Oki, E. Routing and spectrum allocation in elastic optical networks: A tutorial. IEEE Commun. Surv. Tutor. 2015, 17, 1776–1800. [Google Scholar] [CrossRef]
- Dong, Z.; Khan, F.N.; Sui, Q.; Zhong, K.; Lu, C.; Lau, A.P.T. Optical performance monitoring: A review of current and future technologies. J. Lightwave Technol. 2016, 34, 525–543. [Google Scholar] [CrossRef]
- Wang, D.; Jiang, H.; Liang, G.; Zhan, Q.; Mo, Y.; Sui, Q.; Li, Z. Optical Performance Monitoring of Multiple Parameters in Future Optical Networks. J. Lightwave Technol. 2021, 39, 3792–3800. [Google Scholar] [CrossRef]
- Thyagaturu, A.S.; Mercian, A.; McGarry, M.P.; Reisslein, M.; Kellerer, W. Software defined optical networks (SDONs): A comprehensive survey. IEEE Commun. Surv. Tutor. 2016, 18, 2738–2786. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Yu, F.R.; Huang, T.; Xie, R.; Liu, J.; Wang, C.; Liu, Y. A survey of machine learning techniques applied to software defined networking (SDN): Research issues and challenges. IEEE Commun. Surv. Tutor. 2018, 21, 393–430. [Google Scholar] [CrossRef]
- FG-ML5G, I. Focus Group on Machine Learning for Future Networks Including 5G. Available online: https://www.itu.int/en/ITU-T/focusgroups/ml5g/Pages/default.aspx (accessed on 21 December 2021).
- Pointurier, Y. Machine learning techniques for quality of transmission estimation in optical networks. J. Opt. Commun. Netw. 2021, 13, B60–B71. [Google Scholar] [CrossRef]
- Saif, W.S.; Esmail, M.A.; Ragheb, A.M.; Alshawi, T.A.; Alshebeili, S.A. Machine learning techniques for optical performance monitoring and modulation format identification: A survey. IEEE Commun. Surv. Tutor. 2020, 22, 2839–2882. [Google Scholar] [CrossRef]
- Tanaka, T.; Inui, T.; Kawai, S.; Kuwabara, S.; Nishizawa, H. Monitoring and diagnostic technologies usingdeep neural networks for predictive optical network maintenance. J. Opt. Commun. Netw. 2021, 13, E13–E22. [Google Scholar] [CrossRef]
- Tanimura, T.; Hoshida, T.; Kato, T.; Watanabe, S.; Morikawa, H. Convolutional neural network-based optical performance monitoring for optical transport networks. J. Opt. Commun. Netw. 2019, 11, A52–A59. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, A.; Guo, P.; He, P. OSNR and nonlinear noise power estimation for optical fiber communication systems using LSTM based deep learning technique. Opt. Express 2018, 26, 21346–21357. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Q.; Yang, Y.; Zhang, Q.; Yao, Y. Joint, accurate and robust optical signal-to-noise ratio and modulation format monitoring scheme using a single Stokes-parameter-based artificial neural network. Opt. Express 2021, 29, 7276–7287. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Yu, Z.; Wan, Z.; Hu, S.; Shu, L.; Zhang, J.; Xu, K. Low Complexity OSNR Monitoring and Modulation Format Identification Based on Binarized Neural Networks. J. Lightwave Technol. 2020, 38, 1314–1322. [Google Scholar] [CrossRef]
- Saif, W.S.; Alshawi, T.; Esmail, M.A.; Ragheb, A.; Alshebeili, S. Separability of histogram based features for optical performance monitoring: An investigation using t-SNE technique. IEEE Photonics J. 2019, 11, 1–12. [Google Scholar] [CrossRef]
- Shen, T.S.R.; Meng, K.; Lau, A.P.T.; Dong, Z.Y. Optical performance monitoring using artificial neural network trained with asynchronous amplitude histograms. IEEE Photonics Technol. Lett. 2010, 22, 1665–1667. [Google Scholar] [CrossRef]
- Cheng, Y.; Fu, S.; Tang, M.; Liu, D. Multi-task deep neural network (MT-DNN) enabled optical performance monitoring from directly detected PDM-QAM signals. Opt. Express 2019, 27, 19062–19074. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, W.; Fu, S.; Tang, M.; Liu, D. Transfer learning simplified multi-task deep neural network for PDM-64QAM optical performance monitoring. Opt. Express 2020, 28, 7607–7617. [Google Scholar] [CrossRef]
- Jargon, J.A.; Wu, X.; Willner, A.E. Optical performance monitoring by use of artificial neural networks trained with parameters derived from delay-tap asynchronous sampling. In Proceedings of the 2009 Conference on Optical Fiber Communication, San Diego, CA, USA, 22–26 March 2009; pp. 1–3. [Google Scholar]
- Khan, F.N.; Zhou, Y.; Sui, Q.; Lau, A.P.T. Non-data-aided joint bit-rate and modulation format identification for next-generation heterogeneous optical networks. Opt. Fiber Technol. 2014, 20, 68–74. [Google Scholar] [CrossRef]
- Tan, M.C.; Khan, F.N.; Al-Arashi, W.H.; Zhou, Y.; Lau, A.P.T. Simultaneous optical performance monitoring and modulation format/bit-rate identification using principal component analysis. J. Opt. Commun. Netw. 2014, 6, 441–448. [Google Scholar] [CrossRef]
- Fan, X.; Xie, Y.; Ren, F.; Zhang, Y.; Huang, X.; Chen, W.; Zhangsun, T.; Wang, J. Joint optical performance monitoring and modulation format/bit-rate identification by CNN-based multi-task learning. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Khan, F.N.; Fan, Q.; Lu, C.; Lau, A.P.T. An optical communication’s perspective on machine learning and its applications. J. Lightwave Technol. 2019, 37, 493–516. [Google Scholar] [CrossRef]
- Wang, D.; Wang, M.; Zhang, M.; Zhang, Z.; Yang, H.; Li, J.; Li, J.; Chen, X. Cost-effective and data size–adaptive OPM at intermediated node using convolutional neural network-based image processor. Opt. Express 2019, 27, 9403–9419. [Google Scholar] [CrossRef]
- Luo, H.; Huang, Z.; Wu, X.; Yu, C. Cost-Effective Multi-Parameter Optical Performance Monitoring Using Multi-Task Deep Learning With Adaptive ADTP and AAH. J. Lightwave Technol. 2021, 39, 1733–1741. [Google Scholar] [CrossRef]
- Saif, W.S.; Ragheb, A.M.; Alshawi, T.A.; Alshebeili, S.A. Optical Performance Monitoring in Mode Division Multiplexed Optical Networks. J. Lightwave Technol. 2020, 39, 491–504. [Google Scholar] [CrossRef]
- Snyder, A.W.; Love, J. Optical Waveguide Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Garth, S.J. Few-Mode Optical Waveguides and Their Study by the Four-Photon Mixing Process. Ph.D. Thesis, The Australian National University, Canberra, Australia, 1987. [Google Scholar]
- Dods, S.D.; Anderson, T.B. Optical performance monitoring technique using delay tap asynchronous waveform sampling. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 5–10 March 2006; p. OThP5. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Olshausen, B.A.; Field, D.J. Sparse coding with an overcomplete basis set: A strategy employed by V1? Vis. Res. 1997, 37, 3311–3325. [Google Scholar] [CrossRef] [Green Version]
- VPIphotonics. VPItransmissionMaker Optical Systems–Overview. Available online: https://www.vpiphotonics.com/Tools/OpticalSystems/ (accessed on 20 January 2022).
- Vuong, J.; Ramantanis, P.; Frignac, Y.; Salsi, M.; Genevaux, P.; Bendimerad, D.F.; Charlet, G. Mode coupling at connectors in mode-division multiplexed transmission over few-mode fiber. Opt. Express 2015, 23, 1438–1455. [Google Scholar] [CrossRef] [Green Version]
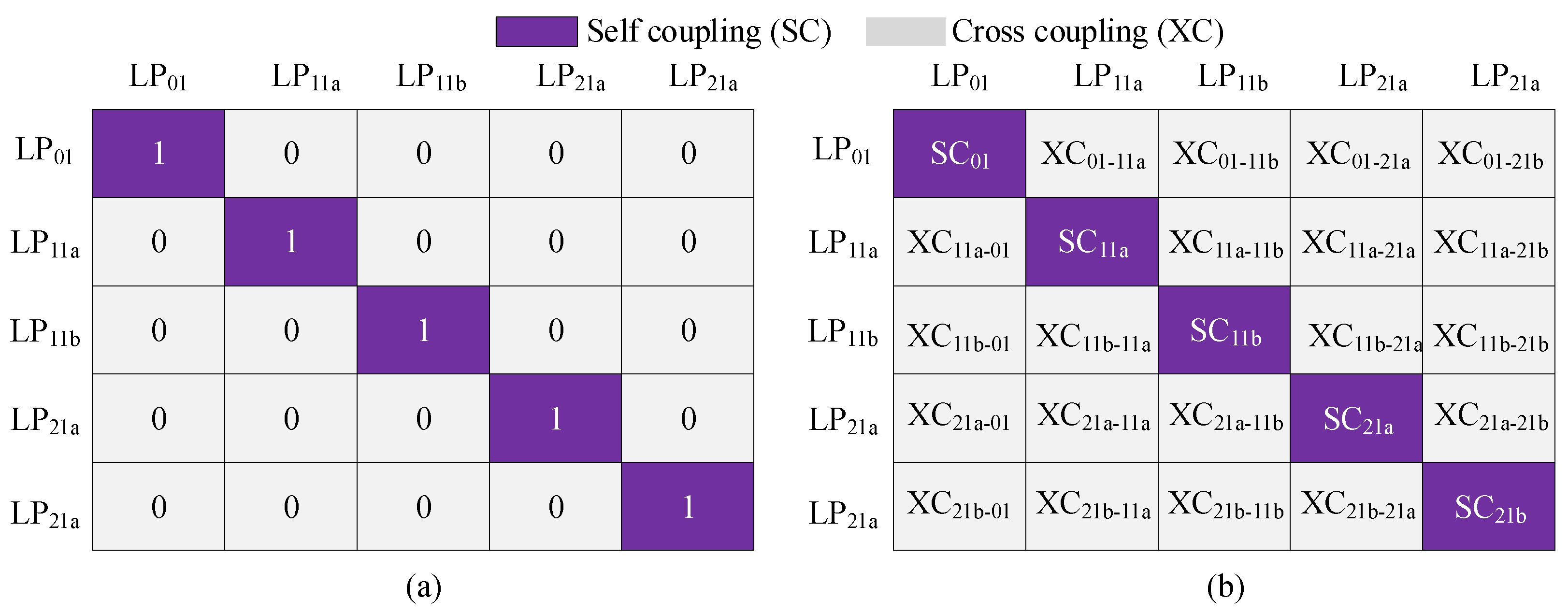

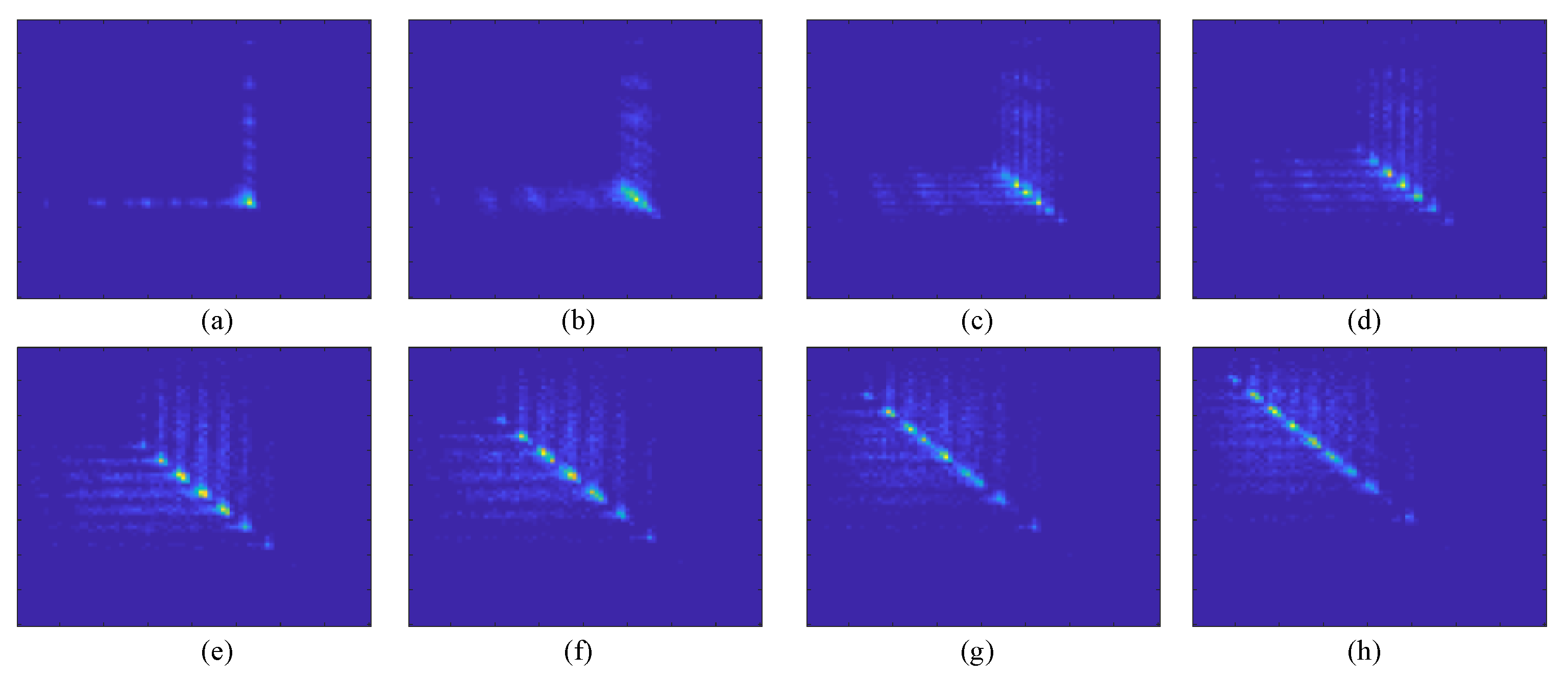
| Case 1 (Light) | Case 2 (Moderate) | Case 3 (Severe) | |
|---|---|---|---|
| OSNR | CD = 160 ps/nm MC = 0.96 | CD = 550 ps/nm MC = 0.74 | CD = 1100 ps/nm MC = 0.47 |
| CD | OSNR = 20 dB MC = 0.96 | OSNR = 14 dB MC = 0.74 | OSNR = 8 dB MC = 0.47 |
| MC | OSNR = 20 dB CD = 160 ps/nm | OSNR = 14 dB CD = 550 ps/nm | OSNR = 8 dB CD = 1100 ps/nm |
| RMSE of OSNR (B) | RMSE of CD (ps/nm) | RMSE of MC | |||||||
|---|---|---|---|---|---|---|---|---|---|
| AAH | ADTH | ADTH-AE | AAH | ADTH | ADTH-AE | AAH | ADTH | ADTH-AE | |
| Case 1 (light) | 0.07 | 0.06 | 0.0015 | 2.15 | 1.33 | 0.28 | 8 × 10−4 | 7 × 10−4 | 7.88 × 10−6 |
| Case 2 (moderate) | 0.16 | 0.12 | 0.004 | 203 | 76 | 37 | 24 × 10−3 | 23 × 10−3 | 3.18 × 10−5 |
| Case 3 (severe) | 0.17 | 0.16 | 0.06 | 633 | 389 | 302 | 28 × 10−3 | 26 × 10−3 | 1 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saif, W.S.; Ragheb, A.M.; Esmail, M.A.; Marey, M.; Alshebeili, S.A. Machine Learning Based Low-Cost Optical Performance Monitoring in Mode Division Multiplexed Optical Networks. Photonics 2022, 9, 73. https://doi.org/10.3390/photonics9020073
Saif WS, Ragheb AM, Esmail MA, Marey M, Alshebeili SA. Machine Learning Based Low-Cost Optical Performance Monitoring in Mode Division Multiplexed Optical Networks. Photonics. 2022; 9(2):73. https://doi.org/10.3390/photonics9020073
Chicago/Turabian StyleSaif, Waddah S., Amr M. Ragheb, Maged A. Esmail, Mohamed Marey, and Saleh A. Alshebeili. 2022. "Machine Learning Based Low-Cost Optical Performance Monitoring in Mode Division Multiplexed Optical Networks" Photonics 9, no. 2: 73. https://doi.org/10.3390/photonics9020073
APA StyleSaif, W. S., Ragheb, A. M., Esmail, M. A., Marey, M., & Alshebeili, S. A. (2022). Machine Learning Based Low-Cost Optical Performance Monitoring in Mode Division Multiplexed Optical Networks. Photonics, 9(2), 73. https://doi.org/10.3390/photonics9020073





