Topological Charge of Multi-Color Optical Vortices
Abstract
:1. Introduction
2. Topological Charge of a Two-Color Superposition of Optical Vortices
3. Numerical Simulation
3.1. Visualization of Polychromatic Beams
3.2. Numerical Simulation of Two-Color Laguerre–Gaussian Vortices with Different Topological Charges
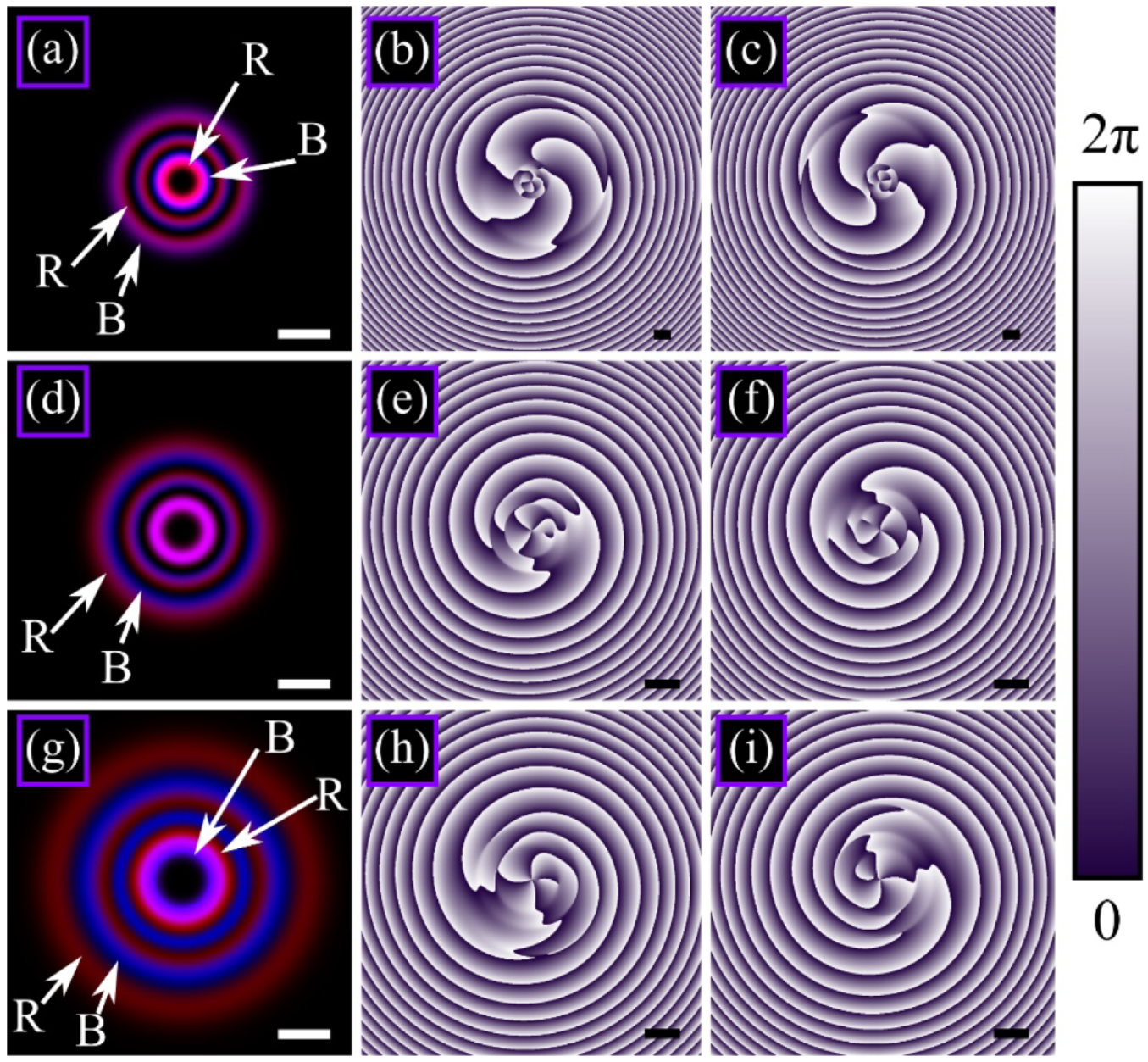
3.3. Numerical Simulation of a Three-Color Laguerre–Gaussian Vortex with Different Topological Charges
3.4. Numerical Simulation of Three-Color Laguerre–Gaussian Vortex with Different Permutations of Light Rings Colors
3.5. Numerical Simulation of a Three-Color Superposition of the Laguerre–Gaussian Vortex with the Same Topological Charge
3.6. Numerical Simulation of Paraxial Free-Space Space Propagation of a Three-Color Gaussian Beam Passed through a Spiral Phase Plate
3.7. FDTD Simulation of the Propagation a Three-Color Gaussian Beam through a Refractive Spiral Phase Plate and in the Near Field
4. Topological Charge of a White Optical Vortex
5. Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kotlyar, V.V.; Kovalev, A.A. Topological Charge of Optical Vortices; Novaya Tekhnika: Samara, Russia, 2021. [Google Scholar]
- Gbur, G.; Tyson, R.K. Vortex beam propagation through atmospheric turbulence and topological charge conservation. J. Opt. Soc. Am. A 2008, 25, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zeng, J.; Duan, M. Classification of coherent vortices creation and distance of topological charge conservation in non-Kolmogorov atmospheric turbulence. Opt. Express 2015, 23, 11556–11565. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Situ, G. Recovery of the topological charge of a vortex beam propagated through a scattering layer. Appl. Opt. 2021, 60, B95–B99. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A.; Amiri, P.; Soltani, P.; Rasouli, S. Topological charge of two parallel Laguerre-Gaussian beams. Opt. Express 2021, 29, 42962–42977. [Google Scholar] [CrossRef]
- Pu, M.; Li, X.; Ma, X.; Wang, Y.; Zhao, Z.; Wang, C.; Hu, C.; Gao, P.; Huang, C.; Ren, H.; et al. Topological charge of two parallel Laguerre-Gaussian beams. Sci. Adv. 2015, 1, 1500396. [Google Scholar] [CrossRef] [Green Version]
- Ponomarenko, S.A.; Wolf, E. Spectral anomalies in a Fraunhofer diffraction pattern. Opt. Lett. 2002, 27, 1211–1213. [Google Scholar] [CrossRef]
- Berry, M.V. Coloured phase singularities. New J. Phys. 2002, 4, 66. [Google Scholar] [CrossRef]
- Leach, J.; Padgett, M. Observation of chromatic effects near a white-light vortex. New J. Phys. 2003, 5, 154. [Google Scholar] [CrossRef]
- Volyar, A.V.; Fadeeva, T.A. Generation of singular beams in uniaxial crystals. Opt. Spectrosc. 2003, 94, 235–244. [Google Scholar] [CrossRef]
- Angelsky, O.V.; Maksimyak, A.P.; Maksimyak, P.P.; Hanson, S.G. Interference diagnostics of white-light vortices. Opt. Express 2005, 13, 8179–8183. [Google Scholar] [CrossRef]
- Arkhelyuk, O.O.; Polyanskii, P.V.; Ivanovskii, A.A.; Soskin, M.S. Creation and diagnostics of stable rainbow optical vortices. Opt. Appl. 2004, 34, 419–426. [Google Scholar]
- Denisenko, V.; Shvedov, V.; Desyatnikov, A.S.; Neshev, D.N.; Krolikovski, W.; Volyar, A.; Soskin, M.; Kivshar, Y.S. Deter-mination of topological charges of polychromatic optical vortices. Opt. Express 2009, 17, 23374–23379. [Google Scholar] [CrossRef] [PubMed]
- Hakobyan, D.; Magallanes, H.; Seniutinas, G.; Juodkazis, S.; Brasselet, E. Tailoring Orbital Angular Momentum of Light in the Visible Domain with Metallic Metasurfaces. Adv. Opt. Mater. 2015, 4, 306–312. [Google Scholar] [CrossRef]
- Kobashi, J.; Yoshida, H.; Ozaki, M. Polychromatic Optical Vortex Generation from Patterned Cholesteric Liquid Crystals. Phys. Rev. Lett. 2016, 116. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, H.; Qiu, X.; Lu, X.; Ren, X.; Chen, L. LED-based chromatic and white-light vortices of fractional topological charges. Opt. Commun. 2020, 485, 126732. [Google Scholar] [CrossRef]
- Tokizane, Y.; Oka, K.; Morita, R. Supercontinuum optical vortex pulse generation without spatial or topological-charge dis-persion. Opt. Express 2009, 17, 14517–14525. [Google Scholar] [CrossRef]
- Anderson, M.E.; Serrano, A.; Stinson, C.; Talamantes, A.; Miller, N.; Chaloupka, J.L. Spatial Manipulation of a Supercontinuum Beam for the Study of Vortex Interference Effects. Appl. Sci. 2020, 10, 1966. [Google Scholar] [CrossRef] [Green Version]
- Siegman, A.E. Lasers; University Science Books: Mill Valley, CA, USA, 1986. [Google Scholar]
- Kotlyar, V.V.; Elfstrom, H.; Turunen, J.; Almazov, A.A.; Khonina, S.; Soifer, V. Generation of phase singularity through diffracting a plane or Gaussian beam by a spiral phase plate. J. Opt. Soc. Am. A 2005, 22, 849–861. [Google Scholar] [CrossRef]
- Vallone, G. On the properties of circular beams: Normalization, Laguerre-Gauss expansion, and free-space divergence. Opt. Lett. 2015, 40, 1717–1720. [Google Scholar] [CrossRef] [Green Version]
- Vallone, G. Role of beam waist in Laguerre-Gauss expansion of vortex beams. Opt. Lett. 2017, 42, 1097–1100. [Google Scholar] [CrossRef]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259–268. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Volyar, A.V. Topological charge of a linear combination of optical vortices: Topological compe-tition. Opt. Express 2020, 28, 8266–8281. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Kölbig, K.S.; Prudnikov, A.P.; Bryckov, Y.A.; Maricev, O.I. Integrals and Series of Special Functions; CRC Press: Boca Raton, FL, USA, 1986. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotlyar, V.V.; Kovalev, A.A.; Nalimov, A.G.; Stafeev, S.S. Topological Charge of Multi-Color Optical Vortices. Photonics 2022, 9, 145. https://doi.org/10.3390/photonics9030145
Kotlyar VV, Kovalev AA, Nalimov AG, Stafeev SS. Topological Charge of Multi-Color Optical Vortices. Photonics. 2022; 9(3):145. https://doi.org/10.3390/photonics9030145
Chicago/Turabian StyleKotlyar, Victor Victorovich, Alexey Andreevich Kovalev, Anton Gennadyevich Nalimov, and Sergey Sergeevich Stafeev. 2022. "Topological Charge of Multi-Color Optical Vortices" Photonics 9, no. 3: 145. https://doi.org/10.3390/photonics9030145




