Gullstrand Intracapsular Accommodation Mechanism Revised

Abstract

More than a century has passed since Allvar Gullstrand proposed his so called “mechanism of intracapsular accommodation” based on the concept that the change in lens power during accommodation can be larger if the lens is modeled by two different refractive indexes (cortex and nucleus) than if it is homogenous. Intracapsular accommodation of the original eye model proposed by Gullstrand is compared with that of a six-surfaces model eye built based on actual experimental data obtained with precise imaging techniques of the lens change during accommodation. The results show that nearly half (42%) of the accommodation of the Gullstrand model eye is produced by said mechanism, while a model eye based on actual data produces a small intracapsular dis-accommodation. The main reason for the discrepancy is the larger change in the radii of curvature of the lens nucleus during accommodation proposed by Gullstrand, which is necessary because his model likely did not take into account the reduction in the change in lens power produced by depth-of-focus.

1. Introduction

Swedish ophthalmologist Allvar Gullstrand’s innovative development of the slit lamp and his careful development of a detailed optical model of the human eye earned him the Nobel Prize in 1911 for his studies on the optics of the eye. In his acceptance speech, titled “How I found the mechanism of intracapsular accommodation” [1], he describes an innovative model of human eye accommodation, in which increasing optical power is achieved by a combination of curvature changes to the lens surface, already proposed by Young [2] and Helmholtz [3], and an original new change in power originating inside the lens which he named the “intracapsular mechanism of accommodation” (IMA).

As a result of his research, Dr. Gullstrand proposed a model eye with a gradient index (GRIN) distribution for the lens [4,5]. Gullstrand also proposed a simpler model for the lens made up of four spherical surfaces, two corresponding to the cortex and two to the nucleus, with both regions of the lens having different refractive indices which presumably accounts for the optical effects generated by the GRIN distribution. Figure 1 shows a copy of the original drawings from Gullstrand presented during his Nobel speech, which represents a meridional section of the lens when the eye is relaxed (Figure 1, left) or accommodated (Figure 1, right), corresponding to a subject of an approximate age of 20 years and an accommodation of 10.9 D [1,6]. Possibly for simplicity, Gullstrand proposed symmetry about the equatorial plane of the accommodated nucleus, although he admits that it most likely is not [6]. Comparing both figures, we find that one of the most remarkable changes during accommodation is undergone by the surfaces of the nucleus, whose radii of curvature become much smaller.

Gullstrand, who could only get direct in vivo measurements of the external shape of the lens (the interface between the cortex and nucleus does not reflect enough light to be seen, contrary to the 3rd and 4th Purkinje images), was aware of the difference of the refractive index between the nucleus and the cortex of the lens [1,6]. He also measured the changes of the lens cortex shape during accommodation, which together with the curvature of the cornea and distance between surfaces measured by himself and previous scientists, persuaded him to propose a model eye with six refractive surfaces (two for the cornea and four for the lens) in relaxed and accommodated states.

Gullstrand suggested that the refractive change of the eye during accommodation would be greater if you consider that the lens has more than one refractive index, which is shown in Figure 1, than in the hypothetical case that the refractive index was unique (homogeneous lens). As a result, the refractive change during accommodation of the eye model proposed by Gullstrand is greater for the lens with two different refractive indexes, than that achieved by a lens with a single equivalent refractive index. To quote Gullstrand [1] “Since the refraction of a homogeneous lens of particular shape is given by the refractive index, it follows that if a lens is made having the same shape as that of the eye, firstly at rest and secondly at maximum accommodation with the refractive index in both cases chosen so that the refraction of the homogeneous lens is the same as that of the eye lens, the refractive index of the homogeneous lens corresponding to the state of accommodation must be made larger than that of the lens corresponding to rest”.

The large change in the lens nucleus was due to the way the lens fibers modify within the lens during accommodation. In the words of Gullstrand [1]: “The most notable feature to emerge from a comparison of these two diagrams (Figure 1) is the strikingly large change in shape undergone by the innermost of the two drawn isoindicial surfaces. These two surfaces change and tend to become spherical, but the inner surface changes most. As shown by a comparison of the two indicial equations, this phenomenon in the drawings is an expression of the fact that the accommodative change in shape of the isoindicial surfaces increases with their proximity to the centre of the lens. On the other hand it follows from the mathematical analysis that this condition corresponds to an accommodative increase in refraction greater than the one that would be brought about by the change in shape itself if the lens were homogeneous”.

A convenient way of summarizing the optical impact of complex structural changes is to represent them as a change in refractive index. For example, Gullstrand’s reduced eye model includes a refractive index of water, which significantly underestimates the actual refractive index of many of the eye’s optical components. More familiar to clinicians is the strategy of employing a refractive index for the cornea that is lower than reality in order to convert anterior corneal radii measured with a keratometer into total corneal power. Gullstrand, and some years later Le Grand [7], employed the same approach to quantify the increase in power of the eye’s homogeneous lens during accommodation that is not explained by change in surface curvature. Therefore, if the lens nucleus contributes added power to the lens when accommodated, the impact of this structural change can be characterized by an increase in the equivalent refractive index (the refractive index required to achieve measured power with surface curvature of outer lens surface if the lens had a single homogeneous refractive index). This approach is convenient for generating the required optical power, but it clearly misrepresents the reality of the lens, as noted by Gullstrand [1]: “But it is this same imaginary refractive index which, as I have previously mentioned, has been termed the total index of the eye lens. Thus in the eye the total index of the lens increases during accommodation, a truly remarkable situation although as we have seen, the total index is not a physical refractive index but an imaginary concept”. Although Gullstrand employed the computation convenience of “equivalent refractive index”, his model (see Figure 1) achieves the change in optical power during accommodation by changing surface curvatures and not refractive indices. So the intracapsular accommodation proposed by Gullstrand does not indicate an increase in the cortex or nucleus indices of refraction during accommodation.

During the last 100 years, the intracapsular mechanism proposed by Gullstrand has been studied by several research groups [8,9,10,11,12,13,14,15,16,17]. Although some studies found evidence of an intracapsular mechanism with an increase of the equivalent refractive index of the lens during accommodation [8,9,12,13], others found no evidence of such a mechanism [10,11,14].

In 1933, Koch and Fisher [8] showed that the external zones of the lens nucleus change their shape during accommodation in the same direction as the lens external surfaces, while the inner zones of the nucleus do not seem to change their shape. However, Fincham found changes at both the outer and inner zones of the nucleus [9]. Based on a Le Grand model eye [7] and photography of the Purkinje images, Fincham was able to find a small increase in the equivalent refractive index of two young eyes during accommodation, changing from 1.413 to 1.432 and 1.415, respectively [9].

A few years later, Huggert [10], using a slit lamp, studied some zonular cataracts under different accommodation states. He showed that the distance between the anterior surface of the lens and the nucleus increased during accommodation, indicating that there should be some displacements between inner lens shells. Huggert, citing the work from Stanka, Vogt, and Gala [10], said: “The changes in the lens calculated by Gullstrand had not at that time been observed and for many years there was little experimental support for Gullstrand’s calculation”.

In 1997, Garner and Smith [11] published an article about the shape and position of the lens before and after accommodation. They indicated that it was possible to simulate accommodation with a GRIN lens with a central refractive index of 1.406 and 1.3859 for the surface. Their model lens showed a mean equivalent refractive index of 1.4277, which did not change during accommodation.

On the other hand, Dubbelman and collaborators [12], using a similar approach as Garner and colleagues [13], observed an increase in the refractive index equivalent of 0.0015 per diopter of accommodation in accordance with Gullstrand’s theory, and close to 0.001 corresponding to the value used by Le Grand [7]. However, as the authors indicated, their calculations were obtained under the hypothesis that the eye was accommodating perfectly to the object, without taking into account any possible underestimation of accommodation (accommodative lag). This error of accommodation was taken into account by means of an objective refractive state in a second study performed by the same group [14]. They obtained the curvatures and surface positions of the lens of the eye while stimulating accommodation and measuring the wavefront of the contralateral eye. Their measurements and calculations based on a lens with two refractive indices did not show any increase in the equivalent refractive index during accommodation.

Smith et al. [15,16] modeled a GRIN lens with isoindicial elliptical surfaces using the radii of curvature for the lens found by Koretz and collaborators [18]. Their results showed that the change in the power of the lens during accommodation depended on the changes in the isoindicial surfaces within the lens, concluding that the change in the power of the lens during accommodation required an increase in the equivalent refractive index if it was to be calculated using a homogenous lens [16].

From this literature review, it seems that the existence, or not, of the intracapsular mechanism would depend upon the model eye used, which depends on the experimental data obtained to build the model eye. In this article, we analyze this mechanism in the model eye proposed by Gullstrand and another model based on experimental data obtained from actual in vivo measurements using technology with a much higher accuracy than the one used by Gullstrand and his predecessors more than a century ago.

2. Materials and Methods

2.1. Eye Models

The existence of intracapsular accommodation has been studied in two eye models:

• Gullstrand eye model: The original model proposed by Gullstrand called “the exact schematic eye” in relaxed and accommodated (near point at 9.2 cm) states. The model details and measurements and Gullstrand’s calculations with this model can be found in his appendix to Helmholtz’s Physiological Optics [6].
• DB eye model: A two-element lens model based on four surfaces forming a nucleus and a cortex (similar to Gullstrand’s exact model eye), with values based on anatomical data of the cornea and the anterior and posterior radii of the lens by Dubbelman and collaborators [12,14,19], the change in the shape and the position of the lens during accommodation [20], as well as the change in the nucleus of the lens during accommodation [21]. In these studies [12,14,19], the subject fixated on a stimulus (usually a Maltese cross) which apparently approached the subject in steps of 1D by placing negative lenses in front of the subject’s eye. Scheimpflug imaging technology was used to obtain the topography of the cortex and nucleus surfaces of the lens during accommodation [19]. The lens refractive indices (cortex and nucleus) were obtained to match accommodation responses after objective measurements using aberrometry [14].

Table 1. Optical parameters of the original Gullstrand eye model, relaxed (2nd column) and accommodated to a stimulus at 10 cm from the eye (3rd column), and those corresponding to the DB eye model (4th column), where “D” represents the stimulus position in diopters (positive numbers indicate that accommodation is not relaxed), and “age” is measured in years. Distances are in mm.

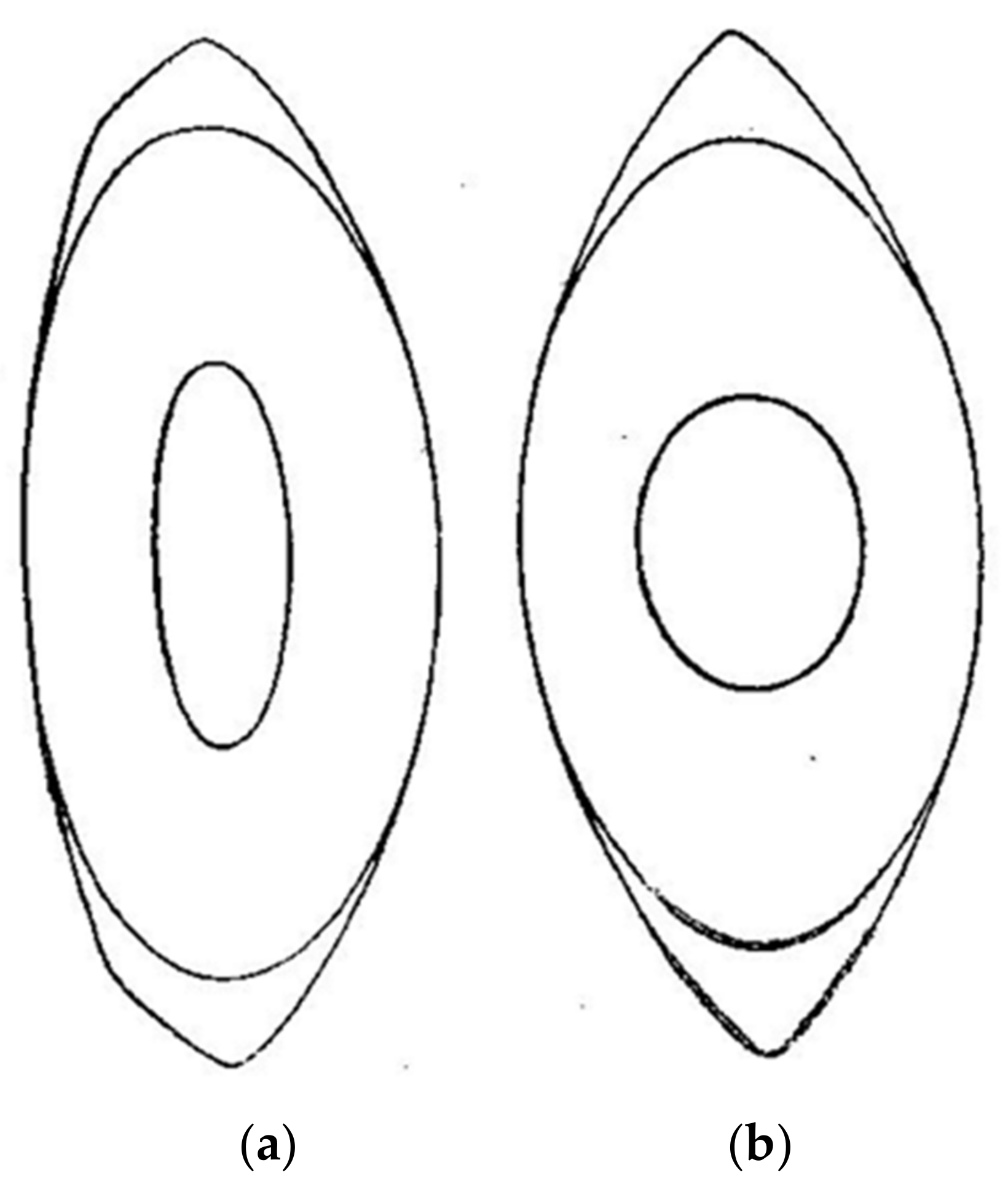
	Gullstrand Eye Model (6 Surf) Relax	Gullstrand Eye Model (6 Surf) Acc	DB Eye Model (6 Surf)
Radius of the anterior surface of the cornea	7.7	7.7	7.87
Q of the anterior surface of the cornea	0	0	0.85
Corneal refractive index	1.376	1.376	1.376
Corneal thickness	0.5	0.5	0.574
Radius of the posterior surface of the cornea	6.8	6.8	6.4
Q of the posterior surface of the cornea	0	0	0.82
Refractive index of the aqueous humor	1.336	1.336	1.336
Anterior chamber depth	3.1	2.7	2.996–0.036 D
Radius of the anterior surface of the lens	10	5.333	1/(0.0894 + 0.0067 D)
Q of the anterior surface of the lens	0	0	−4.5–0.5 D
Refractive index of the cortex lens	1.386	1.386	1.386
Anterior cortex thickness	0.546	0.6725	0.51 + 0.012 Age + 0.004 D
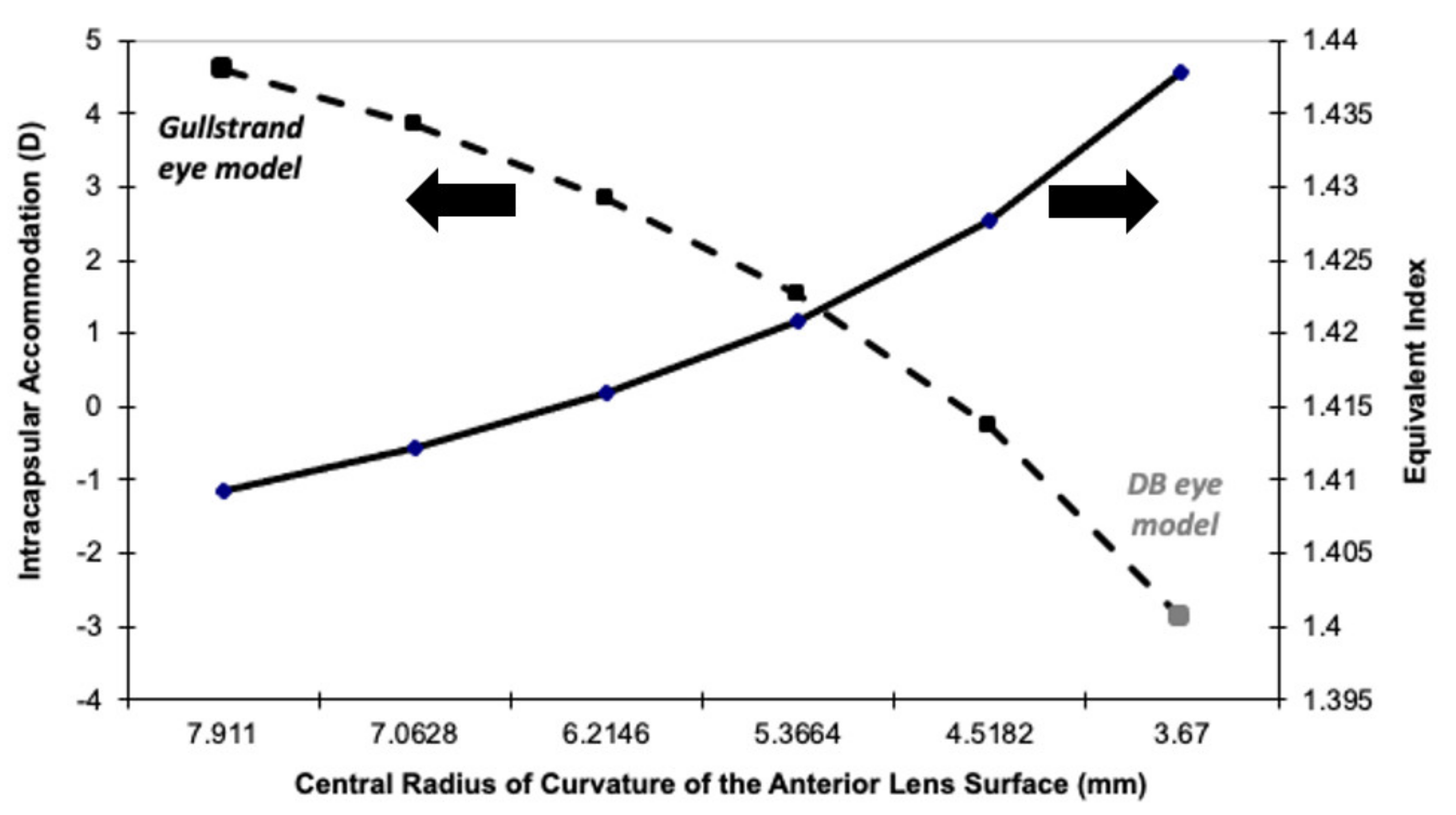
Radius of the anterior nucleus	7.911	2.655	3.67–0.145 D
Q of the ant. and post. surf. of the nucleus	0	0	0
Refractive index of the nucleus	1.406	1.406	1.406
Nucleus thickness	2.419	2.655	2.11 + 0.003 Age + 0.04 D
Radius of the posterior nucleus	−5.76	−2.655	−2.59 + 0.045 D
Posterior cortex thickness	0.635	0.6725	0.33 + 0.0082 Age + 0.0006 D
Radius of the posterior surface of the lens	−6	−5.333	−1/(0.1712 + 0.0037 D)
Q of the posterior surface of the lens	0	0	−1.43
Refractive index of the vitreous humor	1.336	1.336	1.336

shows the data corresponding to both eye models. The original eye model proposed by Gullstrand [6] was composed of six spherical surfaces (asphericity Q = 0 or k = 1), of which the last four correspond to the lens with a refractive index for the nucleus and the cortex of the lens of 1.406 and 1.386, respectively, which do not change between the two refractive states proposed (relaxed and accommodated to a target at 10 cm from the corneal vertex). The DB eye model also presents six surfaces which were not spherical. The change of the shape and position of the lens during accommodation could be calculated by including in each parameter the value “D”, corresponding to the position (in diopters) of the stimulus. Some values also depended on the subject’s age.

As calculated from Table 1, the main differences between the two eye models concerned the shape of the lens nucleus and the presence of asphericity in the surfaces of the model obtained from the data of Dubbelman and coworkers. In particular, for a stimulus at 10 cm (A = 10 D), the anterior and posterior surfaces of the nucleus in Gullstrand’s model eye changed their radius from 7.9 to 2.7 mm (66%) and from 5.8 to 2.7 mm (53%), respectively, while in the DB eye model they changed from 3.7 to 2.2 (41%) and 11.2 to 10.1 mm (9.8%), respectively.

2.2. Paraxial Calculations

Using Gaussian optics, by iterative application of Abbe’s invariant [7] on all the surfaces of the model eye, the position of the object that creates a paraxial image (aberration free) on the retina of the eye can be found.

In our calculations, we have assumed the Gullstrand model eye in the relaxed version to be paraxially emmetropic, while the original eye was hypermetropic by +1 D. Gullstrand created a hypermetropic model eye as he thought that it would better match with a real emmetropic eye due to the presence of high-order aberrations. He said: “Although the exact schematic eye in the passive state has an hypermetropia of one dioptry along axis, so as to represent the actual normal emmetropic eye, this effect of aberration cannot be taken in account in the case of accommodating eye, because the amount of aberration under these circumstances has never yet been ascertained” [6]. Repeating our calculation with a +1 D hyperopic version of Gullstrand’s model resulted in less than 0.1 D change in accommodation with respect to the emmetropic eye shown in Table 1. This is due to the fact that

Table 2. Paraxial and non-paraxial (5 mm pupil) accommodation of the two eye models in Table 1, for a vergence change of 10 D. The equivalent refractive index corresponded to the refractive index for a homogeneous lens that had the same accommodation as the two-component lens with outer surface changes in the two surfaces lens of the relaxed eye.

	Gullstrand Eye Model (6 Surf) Acc	Gullstrand Eye Model (4 Surf) Acc	DB Eye Model (6 Surf) Acc	DB Eye Model (4 Surf) Acc
AA (paraxial) (D) Lens equivalent index	10.9	6.31.409	7.9	8.2 1.439
AA (no paraxial)(D) Lens equivalent index	14.0	6.8 1.409	6.7	7.1 1.439

represents the differences between two refractive states, and thus ametropia practically played no role in the accommodation results, as can be expected from a previous study [22].

To analyze the intracapsular mechanism, we took the following steps:

• The position of the image of an object formed at infinity through each of the six spherical surfaces of the relaxed model eye in Table 1 was found. This gave us the axial length of the emmetropic eye.
• The position of the object that forms an image on the retina of the accommodated eye was found. The vergence of that object corresponded to the paraxial accommodation of the eye.
• The equivalent refractive index (n_eq) of the relaxed emmetropic eye, using the same model eye as in step 1, but with a cortex and nucleus of the lens with the same index of refraction (n_eq), was calculated.
• The accommodation in the eye with a homogeneous lens (step 3) was calculated in a similar way to the heterogeneous lens (step 2), but this time only employing the lens surface changes and n_eq that was already calculated (step 3).

2.3. Non-Paraxial Calculations

A similar procedure as the one used for the paraxial calculations was performed under non-paraxial optics, using the ray-tracing software Zemax-EE for a 5 mm pupil. In this case, the conjugate plane of the object was computed as the one that showed the minimum variance of the wavefront, that is, the minimum RMS [23] that was largely affected by the presence of spherical aberration in the Gullstrand eye model with spherical surfaces.

2.4. Gradient of Curvature

Recently, the importance of a parameter that should be taken into account when studying the power of the gradient index lens, and how the curvature of the isoindicial surfaces change during accommodation has been pointed out [24]. A parameter that can be used to describe that change is the gradient of curvature of the isoindicial surfaces, G (assuming that they are spherical). Parallel isoindicial surfaces correspond to G = 0, while G > 0 or G < 0 corresponds to when their radius reduces or increases, respectively, as they approach the lens center.

Change in the G value during accommodation can be obtained in both eye models from both sides (anterior and rear) of the lens by computing the slope of the change in curvature between the surface of the cortex and that of the nucleus. The results will shed light on the relation between IMA and G.

3. Results

Table 2 shows the results of the accommodation of the two model eyes in Table 1 for a stimulus vergence of −10 D, as well as the equivalent refractive index calculated for the model eye with four surfaces (homogenous lens).

The IMA of both eye models can be computed by subtracting the AA of the four-surface model from that of the six-surface model, resulting in 4.6 D and −0.28 D under paraxial approximation for Gullstrand and DB eye models, respectively. Thus, 42% of the total accommodation is performed by the IMA in the Gullstrand eye model, that is, the AA is much higher in the six-surface model than in the four-surface model. However, the BD model with four surfaces just accommodated 4% more than the six-surface model. Thus, the contribution of the internal nucleus to AA has in both models the opposing sign, and is about 10 times larger in the Gullstrand model than in the DB model.

The main factor responsible for this difference is the radius of curvature of the anterior surface of the nucleus of the relaxed eye (7.91 mm and 3.67 mm for the Gullstrand and DB eye models, respectively; see Table 1). If Gullstrand had used a lower radius for his model (3.67 mm), it would present an intraocular dis-accommodation mechanism (IMA ≈ −3 D). Figure 2 confirms this fact by showing the transition of the equivalent refractive index and the intracapsular paraxial accommodation (computed as the accommodation of the eye modeled with six surfaces minus the accommodation of the eye modeled with four surfaces), from the Gullstrand eye model to the DB eye model eye. A linear decrease in the radius of the anterior surface of the lens core was assumed.

Figure 3 shows the G values at 0 and 10 of stimulus vergence obtained from the slope of the change in curvature of the two eye models, using the data from the anterior and posterior part of the lens independently.

4. Discussion

The main difference between the Gullstrand and DB eye model was the change in the shape of the nucleus radius during accommodation. As indicated previously, nuclear radii of curvature in the Gullstrand model eye were much larger than the DB eye model (see Table 1). Indeed, it was much larger than any other model eyes proposed in the last 20 years, such as the one from Garner and Smith [11], Popiolek-Masajada and Karsprzak [25], or Navarro and collaborators [26]. In particular, Koretz and colloraborators [27], based on the analysis of Scheimpflug photographic images of the eye for different accommodation states, found that the nuclear anterior and posterior surface radii of curvature changed from about 3.75 mm to 3.2 mm and from −5 mm to −3.3 mm, respectively, for 10 D of accommodation. These changes were much closer to the ones found by Dubbelman and collaborators than the one used by Gullstrand, especially for the anterior surface of the nucleus, from which Gullstrand indicated a change from 7.911 mm to 2.655 mm for 10 D of accommodation (Table 1).

Table 2 and Figure 2 show the intracapsular mechanism of accommodation proposed by Gullstrand in his eye model. However, the model designed according to the measurements obtained by Dubbelman and coworkers did not show such a mechanism, but in that case, we should speak of a slightly “dis-accommodation intracapsular mechanism”, as the four-surface model eye accommodated more than the six-surface one, showing a small negative intracapsular accommodation (see Figure 2 and Table 2).

The results found in the DB model eye largely agreed with that found by Garner and Smith [11], who did not find differences between the amplitude of accommodation calculated from a model eye with a gradient index in comparison with the same model eye with a constant refractive index. In the discussion of their article, these authors already said that the result would depend on the model eye used, as our results clearly showed. A similar result was found by Maceo and collaborators, who studied the in vitro contribution of the gradient refractive index of the lens of non-human primates to the accommodation amplitude [28]. These authors showed that the relative contribution of the gradient index to the total lens power remained constant during accommodation, which implied that there was almost no intracapsular accommodation in primates. However, a few years earlier, the model proposed by Navarro and collaborators in 2007 [26] showed a change in the power of the GRIN lens of about 4 D for 8 D of accommodative demand, while the same lens with a unique refractive index (an estimated value of 1.42) changed its power by about 6 D, showing an intracapsular dis-accommodation.

More recently, relatively complex GRIN models proposed by Goranchov [29] and the application of different gradient curvatures to a previous existing GRIN model [24,26] showed that the larger G > 0 value, the larger the power of the lens. Then, if G increased during accommodation, a positive IMA was expected, although this may depend on how large that increase was. For instance, the DB eye model presented an increasing positive G value during accommodation (Figure 3), but a negative IMA was found (Figure 2). On the other hand, Gullstrand’s eye model, with lower G values than the DB eye model (see Figure 3) showed a larger change (nearly twice) in G value for each side (anterior and posterior) of the lens during accommodation. This indicated that the sign and magnitude of IMA depended strongly on the change in G during accommodation, and therefore it seems critical to know how G changes during accommodation to know the actual accommodation of the eye. In this regard, there are some empirical data related to the change in iso-index surfaces distribution with age [30], apparently indicating that, at least the relaxed lens showed a G > 0 and it decreased with age (which theoretically can explain, at least partially, the lens paradox [31]). Unfortunately, so far there are no accurate in vivo experimental data on GRIN during accommodation, and thus the models proposed up until now have based some of their parameters in assumptions. In particular, the work from Navarro and López-Gil used a G value of 1 (concentric isoindicial surfaces) which stayed constant during accommodation, while the work from Dubbelman et al., [31] seemed to indicate an increase in G during accommodation. Empirical data of the change in the lens gradient index distribution during accommodation are needed to provide its real effect on accommodation, which will allow us to design future devices to restore visual function, such as new accommodative intraocular lenses.

Why did Gullstrand propose such a model? By the beginning of the 20th century, it was already known that the lens had a non-homogenous refractive index, as previously mentioned. However in vivo measurements of the curvatures of the anterior and posterior surface lens nucleus is a difficult task, even today, and impossible at the time, when those measurements were based on the analysis of the Purkinje images, which in the case of the lens nucleus were practically negligeable, especially in the presence of GRIN. Thus, knowing the corneal and lens cortex radii of curvature, using some other distances between surfaces and the refractive index of the cornea which was already known, and assuming that the young eye accommodates perfectly for objects placed at 10 cm, Gullstrand used paraxial optics to find that the radii of curvature of the lens cortex, suggesting a nucleus with two radii of curvature that change in such a way that the calculations matched with the experimental outcomes. Interestingly, he used the same absolute value of radius of curvature for both surfaces of the lens nucleus in the accommodated eye (see Table 1).

As mentioned in the Introduction, Hermans and collaborators explained the results obtained by Gullstrand, taking into account that Gullstrand did not account for the lag of accommodation of the accommodated eye [14]. Nevertheless, it is interesting to know that Gullstrand was aware of the presence of depth of focus in the eye, and especially in the accommodated eye, due to the small pupil produced by accommodative myosis [6]: “…a necessary result of the same pupillary contraction is to draw the practical near point of the schematic eye rather nearer the eye than the exact near point, because the depth of focus has to be added in”. However, paraxial calculations in his model showed a paraxial accommodation of 10.9 D, or 14 D using a minimum RMS metric (see Table 2), which was even larger than the dioptric change of the stimulus (10 D), indicating that not only did his model eye not show an accommodation lag, but rather showed an accommodation lead of 0.9 D. In the case of the minimum RMS metric, the lead was much bigger (4 D) due to the fact that spherical aberration increased as the curvature of the spherical surfaces of the lens increased during accommodation. The increase of spherical aberration during accommodation was different to our actual experimental and theoretical knowledge, which showed a decrease in SA during accommodation due to the hyperbolic shapes of the lens surfaces [30]. Indeed, a positive spherical aberration in the relaxed eye, as is the usual case [32], helps the visual system to see small letters even beyond their paraxial far point, despite a decrease in their contrast [33]. Moreover, accommodative miosis and negative spherical aberration in the accommodated eye, as is also the normal case [32], helps to bring the near point closer [34]. Thus, actual changes in spherical aberration increases depth of focus at both ends of the interval of vision, increasing the subjective amplitude of accommodation [35], a fact that Gullstrand certainly did not take into account in his calculations.

Overall, it is fair to recognize Allvar Gullstrand as the first scientist to show that there was something special in the distribution of the refractive index inside the lens, which may help the eye to accommodate more than a homogenous lens. His findings make actual studies on new eye models based on GRIN lenses of great interest for two reasons. From a fundamental point of view, they may solve the old question as to the real usefulness of the GRIN on accommodation or the explanation of the lens paradox. From a more applied point of view, new eye models based on GRIN will predict retinal image formation and deterioration better and will help to develop new accommodative IOLs which change power with a lower change in the curvature of their surfaces.

In conclusion, Gullstrand’s eye model, which showed for the first time the intracapsular accommodation mechanism, overestimated the real accommodation of the eye (very likely due to the fact that he assumed that the lens changes its power during accommodation more than it really does [19]). To account for such a large power change, Gullstrand proposed a much larger change in the curvature of the surfaces of the nucleus during accommodation than the lens really undergoes.