Investigation of the Way of Phase Synchronization of a Self-Injected Bunch and an Accelerating Wakefield in Solid-State Plasma
Abstract
:1. Introduction
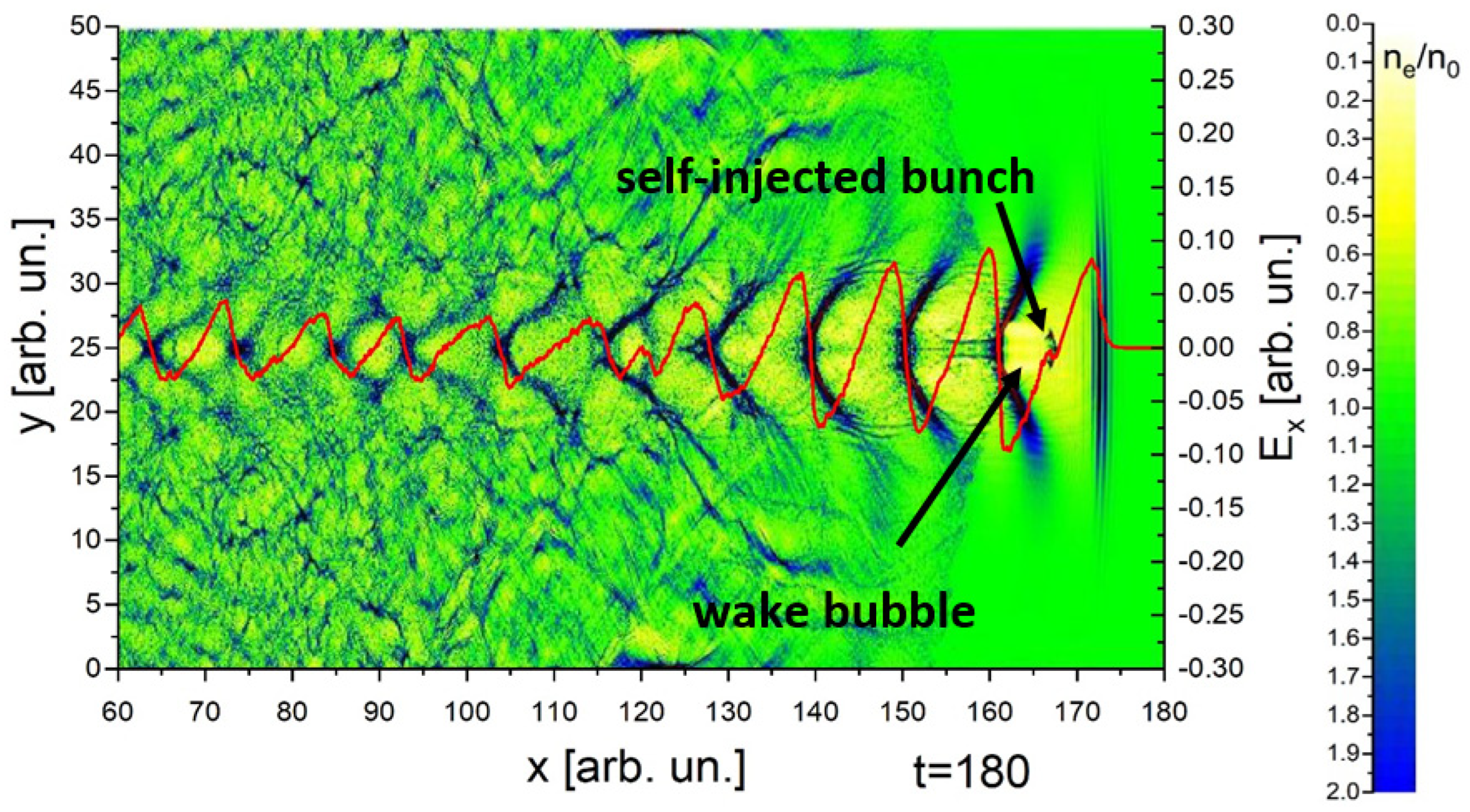
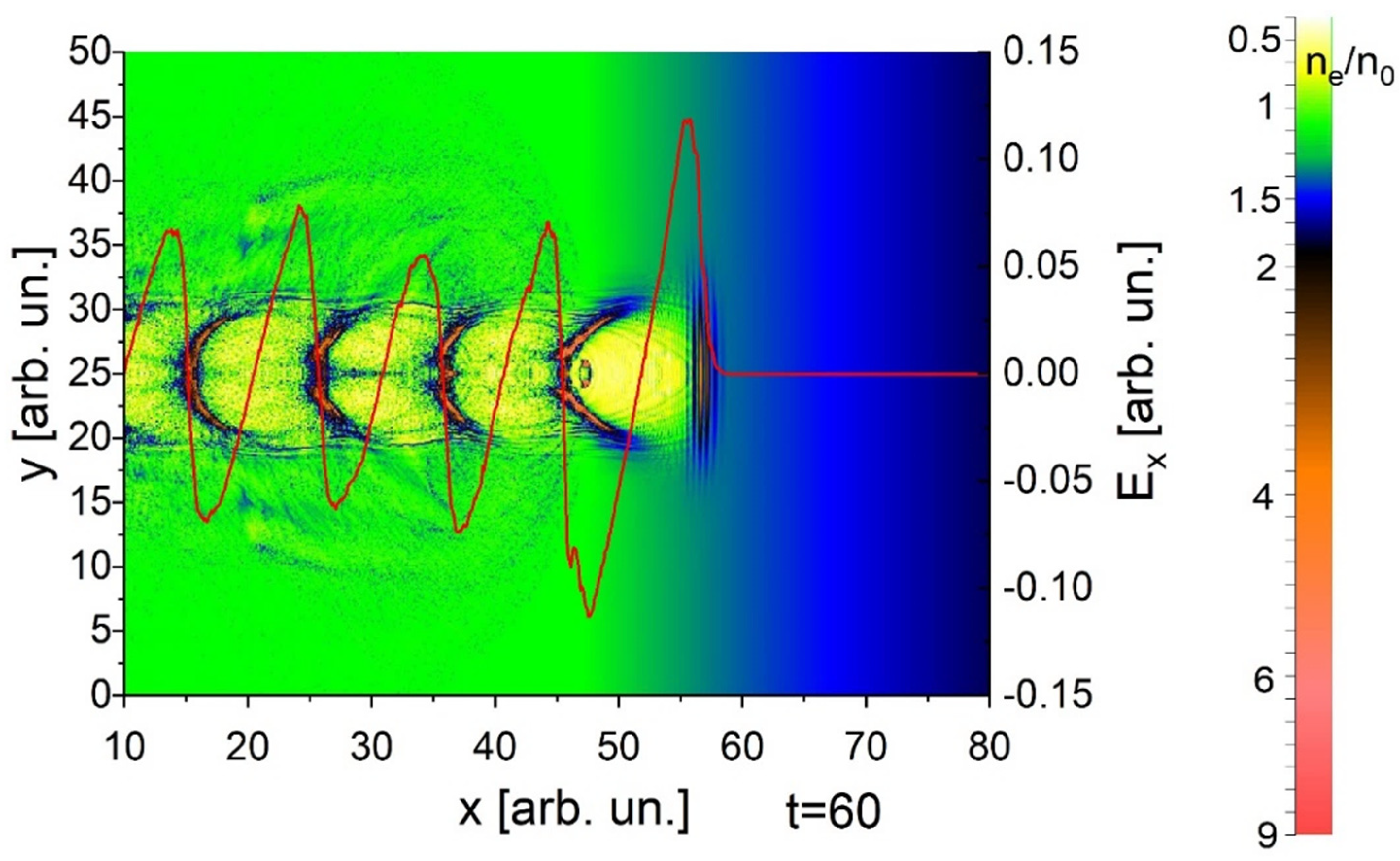
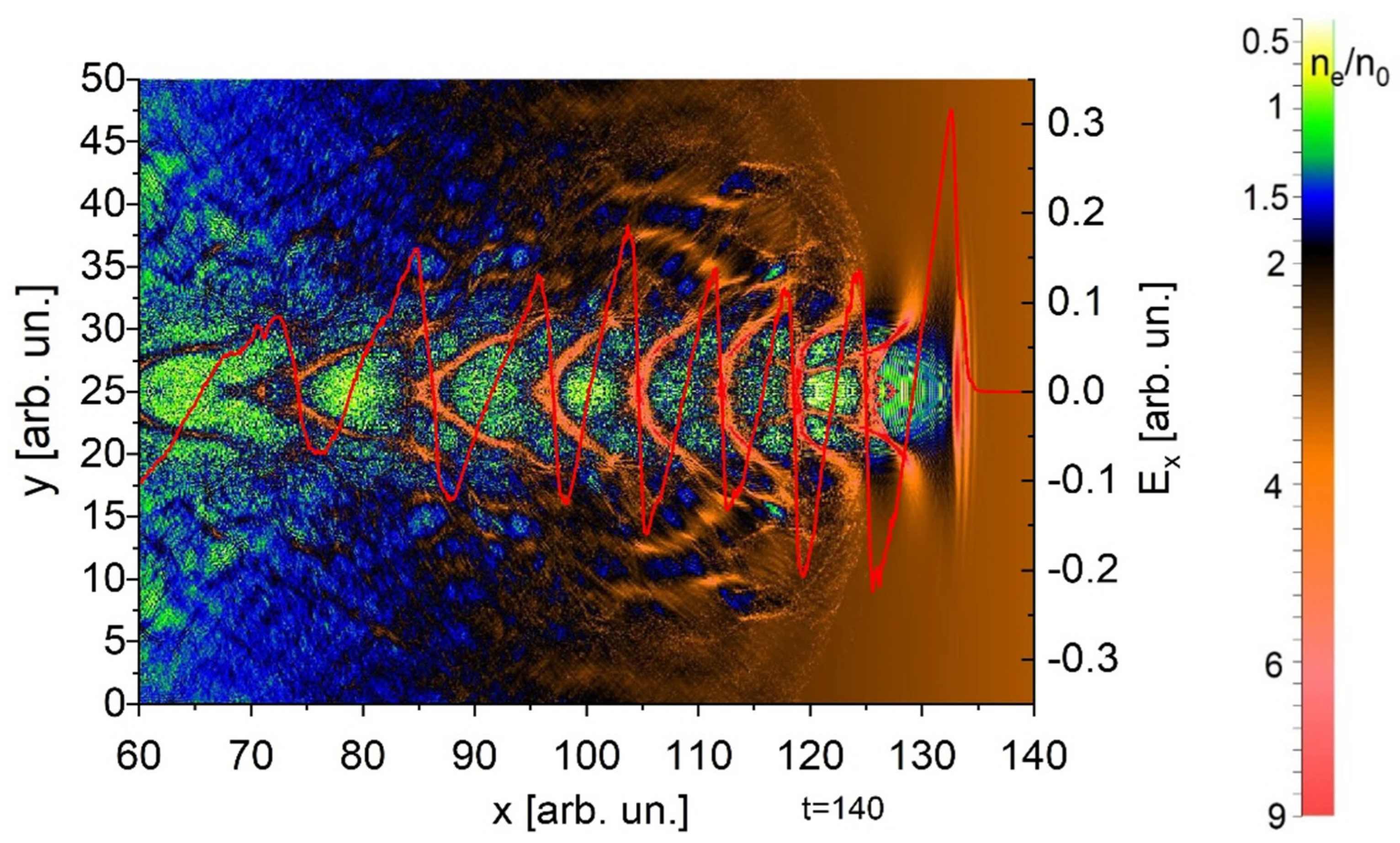
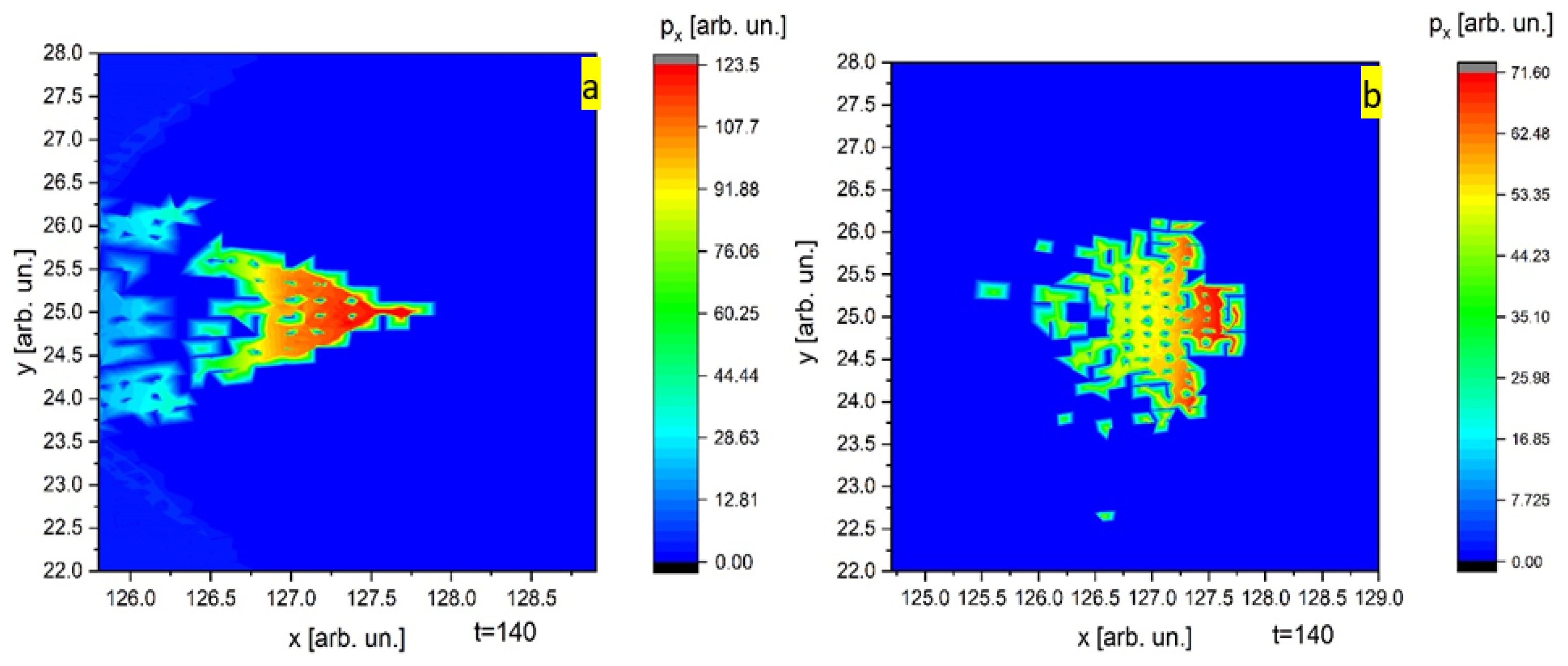
2. Results of Simulation
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brantov, A.V.; Esirkepov, T.Z.; Kando, M.; Kotaki, H.; Bychenkov, V.Y.; Bulanov, S.V. Controlled electron injection into the wake wave using plasma density inhomogeneity. Phys. Plasmas 2008, 15, 073111. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Naumova, N.; Pegoraro, F.; Sakai, J. Particle injection into the wave acceleration phase due to nonlinear wake wave breaking. Phys. Rev. E 1998, 58, R5257. [Google Scholar] [CrossRef] [Green Version]
- Ohkubo, T.; Zhidkov, A.; Hosokai, T.; Kinoshita, K.; Uesaka, M. Effects of density gradient on short-bunch injection by wave breaking in the laser wake field acceleration. Phys. Plasmas 2006, 13, 033110. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Inovenkov, I.N.; Kirsanov, V.I.; Naumova, N.M.; Sakharov, A.S. Nonlinear depletion of ultrashort and relativistically strong laser pulses in an underdense plasma. Phys. Fluids B Plasma Phys. 1992, 4, 1935–1942. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Pegoraro, F.; Pukhov, A.M.; Sakharov, A.S. Transverse-Wake Wave Breaking. Phys. Rev. Lett. 1997, 78, 4205. [Google Scholar] [CrossRef]
- Liseikina, T.V.; Califano, F.; Vshivkov, V.A.; Pegoraro, F.; Bulanov, S.V. Small-scale electron density and magnetic-field structures in the wake of an ultraintense laser pulse. Phys. Rev. E 1999, 60, 5991. [Google Scholar] [CrossRef] [PubMed]
- Tajima, T. Laser acceleration in novel media. Eur. Phys. J. Spec. Top. 2014, 223, 1037–1044. [Google Scholar] [CrossRef]
- Tajima, T.; Nakajima, K.; Mourou, G. Laser acceleration. La Riv. Nuovo Cim. 2017, 40, 33–133. [Google Scholar]
- Bondar, D.S.; Maslov, V.I.; Levchuk, I.P.; Onishchenko, I.N. Excitation of wakefield by a laser pulse in a metallicdensity electron plasma. Probl. At. Sci. Technol. 2018, 6, 156–159. [Google Scholar]
- Albert, F.; Couprie, M.E.; Debus, A.; Downer, M.C.; Faure, J.; Flacco, A.; Gizzi, L.A.; Grismayer, T.; Huebl, A.; Joshi, C.; et al. 2020 roadmap on plasma accelerators. New J. Phys. 2021, 23, 031101. [Google Scholar] [CrossRef]
- Assmann, R.W.; Weikum, M.K.; Akhter, T.; Alesini, D.; Alexandrova, A.S.; Anania, M.P.; Andreev, N.E.; Andriyash, I.; Artioli, M.; Aschikhin, A.; et al. Eupraxia conceptual design report. Eur. Phys. J. Spec. Top. 2020, 229, 3675–4284. [Google Scholar] [CrossRef]
- Dudnikova, G.I.; Liseykina, T.V.; Bychenkov, V.Y. Parallel algorithms for numerical simulation of propagation of an electromagnetic radiation in plasma. Comp. Techn. 2005, 10, 37. [Google Scholar]
- Leemans, W.P.; Gonsalves, A.J.; Mao, H.S.; Nakamura, K.; Benedetti, C.; Schroeder, C.B.; Tóth, C.; Daniels, J.; Mittelberger, D.E.; Bulanov, S.S.; et al. Multi-GeV electron beams from capillary-discharge-guided subpetawatt laser pulses in the self-trapping regime. Phys. Rev. Lett. 2014, 113, 245002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pieronek, C.V.; Gonsalves, A.J.; Benedetti, C.; Bulanov, S.S.; Van Tilborg, J.; Bin, J.H.; Swanson, K.K.; Daniels, J.; Bagdasarov, G.A.; Bobrova, N.A.; et al. Laser-heated capillary discharge waveguides as tunable structures for laser-plasma acceleration. Phys. Plasmas 2020, 27, 093101. [Google Scholar] [CrossRef]
- Hakimi, S.; Nguyen, T.; Farinella, D.; Lau, C.K.; Wang, H.Y.; Taborek, P.; Dollar, F.; Tajima, T. Wakefield in solid state plasma with the ionic lattice force. Phys. Plasmas 2018, 25, 023112. [Google Scholar] [CrossRef]
- Thompson, M.C.; Badakov, H.; Cook, A.M.; Rosenzweig, J.B.; Tikhoplav, R.; Travish, G.; Blumenfeld, I.; Hogan, M.J.; Ischebeck, R.; Kirby, N.; et al. Breakdown limits on gigavolt-per-meter electron-beam-driven wakefields in dielectric structures. Phys. Rev. Lett. 2008, 100, 214801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Danson, C.N.; Haefner, C.; Bromage, J.; Butcher, T.; Chanteloup, J.-C.F.; Chowdhury, E.A.; Galvanauskas, A.; Gizzi, L.A.; Hein, J.; Hillier, D.I. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 2019, 7, e54. [Google Scholar] [CrossRef]
- Kim, T.H.; Pathak, V.B.; Hojbota, C.L.; Mirzaie, M.; Pae, K.H.; Kim, C.M.; Yoon, J.W.; Sung, J.H.; Lee, S.K. Multi-GeV Laser Wakefield Electron Acceleration with PW Lasers. Appl. Sci. 2021, 11, 5831. [Google Scholar] [CrossRef]
- Onishchenko, I.N.; Kiselev, V.A.; Linnik, A.F.; Sotnikov, G.V. Concept of dielectric wakefield accelerator driven by a long sequence of electron bunches. In Proceedings of the IPAC, Shanghai, China, 12–17 May 2013; p. 1259, ISBN 978-3-95450-122-9. [Google Scholar]
- Onishchenko, I.N.; Kiseljob, V.A.; Berezin, A.K.; Sotnikov, G.V.; Uskov, V.V.; Linnik, A.F.; Fainberg, Y.B. The wake-field excitation in plasma-dielectric structure by sequence of short bunches of relativistic electrons. In Proceedings of the Particle Accelerator Conference, Dallas, TX, USA, 1–5 May 1995; p. 2782. [Google Scholar]
- Lotov, K.V.; Maslov, V.I.; Onishchenko, I.N.; Yarovaya, I.P. Mechanisms of synchronization of relativistic electron bunches at wakefield excitation in plasma. Probl. At. Sci. Technol. 2013, 4, 73–76. [Google Scholar]
- Lotov, K.V.; Maslov, V.I.; Onishchenko, I.N. Long sequence of relativistic electron bunches as a driver in wakefield method of charged particles acceleration in plasma. Probl. At. Sci. Technol. 2010, 6, 103–107. [Google Scholar]
- Bondar, D.S.; Maslov, V.I.; Boychenko, A.P.; Ovsiannikov, R.T.; Onishchenko, I.N. Dependence of wakefield excitation in plasma by non-resonant sequence of electron bunches on their lengths. Probl. At. Sci. Technol. 2021, 4, 65–69. [Google Scholar] [CrossRef]
- Lotov, K.V.; Maslov, V.I.; Onishchenko, I.N. Transformation ratio in wake-field method of acceleration for sequence of relativistic electron bunches. Probl. At. Sci. Technol. 2010, 4, 85–89. [Google Scholar]
- Baturin, S.S.; Zholents, A. Upper limit for the accelerating gradient in the collinear wakefield accelerator as a function of the transformer ratio. Phys. Rev. Accel. Beams 2017, 20, 061302. [Google Scholar] [CrossRef] [Green Version]
- Marzbanrad, B.; Toyserkani, E.; Jahed, H. Characterization of single-and multilayer cold-spray coating of Zn on AZ31B. Surf. Coat. Technol. 2021, 416, 127155. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maslov, V.I.; Bondar, D.S.; Onishchenko, I.N. Investigation of the Way of Phase Synchronization of a Self-Injected Bunch and an Accelerating Wakefield in Solid-State Plasma. Photonics 2022, 9, 174. https://doi.org/10.3390/photonics9030174
Maslov VI, Bondar DS, Onishchenko IN. Investigation of the Way of Phase Synchronization of a Self-Injected Bunch and an Accelerating Wakefield in Solid-State Plasma. Photonics. 2022; 9(3):174. https://doi.org/10.3390/photonics9030174
Chicago/Turabian StyleMaslov, Vasyl I., Denys S. Bondar, and Ivan N. Onishchenko. 2022. "Investigation of the Way of Phase Synchronization of a Self-Injected Bunch and an Accelerating Wakefield in Solid-State Plasma" Photonics 9, no. 3: 174. https://doi.org/10.3390/photonics9030174
APA StyleMaslov, V. I., Bondar, D. S., & Onishchenko, I. N. (2022). Investigation of the Way of Phase Synchronization of a Self-Injected Bunch and an Accelerating Wakefield in Solid-State Plasma. Photonics, 9(3), 174. https://doi.org/10.3390/photonics9030174




