Segmentation and Quantitative Analysis of Photoacoustic Imaging: A Review
Abstract
:1. Introduction
2. Segmentation and Quantification for PAI
2.1. Classic Segmentation and Quantification Approaches
2.1.1. Thresholding Segmentation
2.1.2. Morphology Segmentation
2.1.3. Wavelet-Based Frequency Segmentation
2.2. Deep Learning Segmentation Approaches
2.2.1. Overview of Deep Learning Segmentation Networks
2.2.2. Supervised Learning Segmentation
2.2.3. Unsupervised Learning Segmentation
3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 41101. [Google Scholar] [CrossRef] [Green Version]
- Gibson, A.P.; Hebden, J.C.; Arridge, S.R. Recent advances in diffuse optical imaging. Phys. Med. Biol. 2005, 50, R1–R43. [Google Scholar] [CrossRef] [PubMed]
- Farsiu, S.; Christofferson, J.; Eriksson, B.; Milanfar, P.; Friedlander, B.; Shakouri, A.; Nowak, R. Statistical detection and imaging of objects hidden in turbid media using ballistic photons. Appl. Opt. 2007, 46, 5805–5822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Durduran, T.; Choe, R.; Baker, W.B.; Yodh, A.G. Diffuse Optics for Tissue Monitoring and Tomography. Rep. Prog. Phys. 2010, 73, 76701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonner, R.F.; Nossal, R.; Havlin, S.; Weiss, G.H. Model for photon migration in turbid biological media. J. Opt. Soc. Am. A 1987, 4, 423–432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, X.; Kim, C.; Pramanik, M.; Wang, L.V. Photoacoustic tomography of foreign bodies in soft biological tissue. J. Biomed. Opt. 2011, 16, 46017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.; Han, S.; Kim, S.; Jeon, M.; Jeon, M.Y.; Kim, C.; Kim, J. Combined photoacoustic and optical coherence tomography using a single near-infrared supercontinuum laser source. Appl. Opt. 2013, 52, 1824–1828. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, C.; Park, K.; Han, S.; Kim, C. High-speed and high-SNR photoacoustic microscopy based on a galvanometer mirror in non-conducting liquid. Sci. Rep. 2016, 6, 34803. [Google Scholar] [CrossRef]
- Lee, D.; Lee, C.; Kim, S.; Zhou, Q.; Kim, J.; Kim, C. In Vivo Near Infrared Virtual Intraoperative Surgical Photoacoustic Optical Coherence Tomography. Sci. Rep. 2016, 6, 35176. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Jeon, M.; Jeon, M.Y.; Kim, J.; Kim, C. In vitro photoacoustic measurement of hemoglobin oxygen saturation using a single pulsed broadband supercontinuum laser source. Appl. Opt. 2014, 53, 3884–3889. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.; Jung, U.; Kim, C. Photoacoustic imaging platforms for multimodal imaging. Ultrasonography 2015, 34, 88–97. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Kwon, O.; Jeon, M.; Song, J.; Shin, S.; Kim, H.; Jo, M.; Rim, T.; Doh, J.; Kim, S.; et al. Super-resolution visible photoactivated atomic force microscopy. Light Sci. Appl. 2017, 6, e17080. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, S.; Maslov, K.; Wang, L.V. Second-generation optical-resolution photoacoustic microscopy with improved sensitivity and speed. Opt. Lett. 2011, 36, 1134–1136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.; Kim, J.Y.; Jeon, S.; Baik, J.W.; Cho, S.H.; Kim, C. Super-resolution localization photoacoustic microscopy using intrinsic red blood cells as contrast absorbers. Light Sci. Appl. 2019, 8, 103. [Google Scholar] [CrossRef]
- Wang, Y.; Maslov, K.I.; Zhang, Y.; Hu, S.; Yang, L.-M.; Xia, Y.; Liu, J.; Wang, L.V. Fiber-laser-based photoacoustic microscopy and melanoma cell detection. J. Biomed. Opt. 2011, 16, 11014. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.-Y.; Lee, C.; Jung, H.S.; Jeon, M.; Kim, K.S.; Yun, S.H.; Kim, C.; Hahn, S.K. Biodegradable Photonic Melanoidin for Theranostic Applications. ACS Nano 2016, 10, 822–831. [Google Scholar] [CrossRef]
- Zhang, Y.; Jeon, M.; Rich, L.J.; Hong, H.; Geng, J.; Zhang, Y.; Shi, S.; Barnhart, T.E.; Alexandridis, P.; Huizinga, J.D.; et al. Non-invasive multimodal functional imaging of the intestine with frozen micellar naphthalocyanines. Nat. Nanotechnol. 2014, 9, 631–638. [Google Scholar] [CrossRef]
- Jeong, S.; Yoo, S.W.; Kim, H.J.; Park, J.; Kim, J.W.; Lee, C.; Kim, H. Recent Progress on Molecular Photoacoustic Imaging with Carbon-Based Nanocomposites. Materials 2021, 14, 5643. [Google Scholar] [CrossRef]
- Lovell, J.F.; Jin, C.S.; Huynh, E.; Jin, H.; Kim, C.; Rubinstein, J.L.; Chan, W.C.W.; Cao, W.; Wang, L.V.; Zheng, G. Porphysome nanovesicles generated by porphyrin bilayers for use as multimodal biophotonic contrast agents. Nat. Mater. 2011, 10, 324–332. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Yang, M.; Zhang, Q.; Cho, E.C.; Cobley, C.M.; Kim, C.; Glaus, C.; Wang, L.V.; Welch, M.J.; Xia, Y. Gold Nanocages: A Novel Class of Multifunctional Nanomaterials for Theranostic Applications. Adv. Funct. Mater. 2010, 20, 3684–3694. [Google Scholar] [CrossRef]
- Kim, C.; Jeon, M.; Wang, L.V. Nonionizing photoacoustic cystography in vivo. Opt. Lett. 2011, 36, 3599–3601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.; Kim, J.; Zhang, Y.; Jeon, M.; Liu, C.; Song, L.; Lovell, J.F.; Kim, C. Dual-color photoacoustic lymph node imaging using nanoformulated naphthalocyanines. Biomaterials 2015, 73, 142–148. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Maslov, K.I.; Zhang, Y.; Xia, Y.; Wang, L.V. Label-free oxygen-metabolic photoacoustic microscopy in vivo. J. Biomed. Opt. 2011, 16, 76003. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Xing, W.; Maslov, K.I.; Cornelius, L.A.; Wang, L.V. Handheld photoacoustic microscopy to detect melanoma depth in vivo. Opt. Lett. 2014, 39, 4731–4734. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Wang, L.V.; Cheng, Y.-J.; Chen, J.; Wickline, S.A. Label-free photoacoustic microscopy of myocardial sheet architecture. J. Biomed. Opt. 2012, 17, 60506. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Wang, L. Neurovascular photoacoustic tomography. Front. Neuroenerg. 2010, 2, 10. [Google Scholar] [CrossRef] [Green Version]
- Jiao, S.; Jiang, M.; Hu, J.; Fawzi, A.; Zhou, Q.; Shung, K.K.; Puliafito, C.A.; Zhang, H.F. Photoacoustic ophthalmoscopy for in vivo retinal imaging. Opt. Express 2010, 18, 3967–3972. [Google Scholar] [CrossRef]
- Wang, L.V. Photoacoustic Imaging and Spectroscopy; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-4200-5992-2. [Google Scholar]
- Lee, C.; Kim, J.Y.; Kim, C. Recent Progress on Photoacoustic Imaging Enhanced with Microelectromechanical Systems (MEMS) Technologies. Micromachines 2018, 9, 584. [Google Scholar] [CrossRef] [Green Version]
- Park, K.; Kim, J.Y.; Lee, C.; Jeon, S.; Lim, G.; Kim, C. Handheld Photoacoustic Microscopy Probe. Sci. Rep. 2017, 7, 13359. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, C.; Park, K.; Lim, G.; Kim, C. Fast optical-resolution photoacoustic microscopy using a 2-axis water-proofing MEMS scanner. Sci. Rep. 2015, 5, 7932. [Google Scholar] [CrossRef]
- Han, S.; Lee, C.; Kim, S.; Jeon, M.; Kim, J.; Kim, C. In vivo virtual intraoperative surgical photoacoustic microscopy. Appl. Phys. Lett. 2013, 103, 203702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, J.; Xia, J.; Maslov, K.I.; Nasiriavanaki, M.; Tsytsarev, V.; Demchenko, A.V.; Wang, L.V. Noninvasive photoacoustic computed tomography of mouse brain metabolism in vivo. Neuroimage 2013, 64, 257–266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.V.; Hu, S. Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs. Science 2012, 335, 1458–1462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chatni, M.R.; Xia, J.; Maslov, K.I.; Guo, Z.; Wang, K.; Anastasio, M.A.; Wang, L.V.; Sohn, R.; Arbeit, J.M.; Zhang, Y.; et al. Tumor glucose metabolism imaged in vivo in small animals with whole-body photoacoustic computed tomography. J. Biomed. Opt. 2012, 17, 76012. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Razansky, D.; Distel, M.; Vinegoni, C.; Ma, R.; Perrimon, N.; Köster, R.W.; Ntziachristos, V. Multispectral opto-acoustic tomography of deep-seated fluorescent proteins in vivo. Nat. Photonics 2009, 3, 412–417. [Google Scholar] [CrossRef]
- Filonov, G.S.; Krumholz, A.; Xia, J.; Yao, J.; Wang, L.V.; Verkhusha, V.V. Deep-Tissue Photoacoustic Tomography of a Genetically Encoded Near-Infrared Fluorescent Probe. Angew. Chem. Int. Ed. 2012, 51, 1448–1451. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Lee, C.; Kim, J.; Kim, C. Acoustic resolution photoacoustic microscopy. Biomed. Eng. Lett. 2014, 4, 213–222. [Google Scholar] [CrossRef]
- Xu, M.; Wang, L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E 2005, 71, 16706. [Google Scholar] [CrossRef] [Green Version]
- Treeby, B.E.; Zhang, E.Z.; Cox, B.T. Photoacoustic tomography in absorbing acoustic media using time reversal. Inverse Probl. 2010, 26, 115003. [Google Scholar] [CrossRef]
- Xia, J.; Yao, J.; Wang, L.V. Photoacoustic Tomography: Principles and Advances (Invited Review). Electromagn. Waves. 2014, 147, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Cox, B.T.; Laufer, J.G.; Beard, P.C.; Arridge, S.R. Quantitative spectroscopic photoacoustic imaging: A review. J. Biomed. Opt. 2012, 17, 61202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cox, B.T.; Arridge, S.R.; Beard, P.C. Estimating chromophore distributions from multiwavelength photoacoustic images. J. Opt. Soc. Am. A 2009, 26, 443–455. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cox, B.T.; Arridge, S.R.; Köstli, K.P.; Beard, P.C. Two-dimensional quantitative photoacoustic image reconstruction of absorption distributions in scattering media by use of a simple iterative method. Appl. Opt. 2006, 45, 1866–1875. [Google Scholar] [CrossRef] [PubMed]
- Cox, B.T.; Arridge, S.R.; Kostli, K.P.; Beard, P.C. Quantitative photoacoustic imaging: Fitting a model of light transport to the initial pressure distribution. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2005: The Sixth Conference on Biomedical Thermoacoustics, Optoacoustics, and Acousto-Optics, San Jose, CA, USA, 22–27 January 2005; Volume 5697, pp. 49–55. [Google Scholar]
- Mai, T.T.; Yoo, S.W.; Park, S.; Kim, J.Y.; Choi, K.-H.; Kim, C.; Kwon, S.Y.; Min, J.-J.; Lee, C. In Vivo Quantitative Vasculature Segmentation and Assessment for Photodynamic Therapy Process Monitoring Using Photoacoustic Microscopy. Sensors 2021, 21, 1776. [Google Scholar] [CrossRef] [PubMed]
- Mai, T.T.; Vo, M.-C.; Chu, T.-H.; Kim, J.Y.; Kim, C.; Lee, J.-J.; Jung, S.-H.; Lee, C. Pilot Study: Quantitative Photoacoustic Evaluation of Peripheral Vascular Dynamics Induced by Carfilzomib in vivo. Sensors 2021, 21, 836. [Google Scholar] [CrossRef]
- Kim, J.; Mai, T.T.; Kim, J.Y.; Min, J.-J.; Kim, C.; Lee, C. Feasibility Study of Precise Balloon Catheter Tracking and Visualization with Fast Photoacoustic Microscopy. Sensors 2020, 20, 5585. [Google Scholar] [CrossRef]
- Allen, T.J.; Beard, P.C.; Hall, A.; Dhillon, A.P.; Owen, J.S. Spectroscopic photoacoustic imaging of lipid-rich plaques in the human aorta in the 740 to 1400 nm wavelength range. J. Biomed. Opt. 2012, 17, 61209. [Google Scholar] [CrossRef]
- Cao, Y.; Kole, A.; Hui, J.; Zhang, Y.; Mai, J.; Alloosh, M.; Sturek, M.; Cheng, J.-X. Fast assessment of lipid content in arteries in vivo by intravascular photoacoustic tomography. Sci. Rep. 2018, 8, 2400. [Google Scholar] [CrossRef]
- Xu, M.; Lei, P.; Feng, J.; Liu, F.; Yang, S.; Zhang, P. Photoacoustic characteristics of lipid-rich plaques under ultra-low temperature and formaldehyde treatment. Chin. Opt. Lett. 2018, 16, 31702. [Google Scholar]
- Yao, J.; Wang, L.V. Photoacoustic microscopy. Laser Photonics Rev. 2013, 7, 758–778. [Google Scholar] [CrossRef]
- Xia, J.; Wang, L.V. Small-Animal Whole-Body Photoacoustic Tomography: A Review. IEEE Trans. Biomed. Eng. 2014, 61, 1380–1389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, C.; Lan, H.; Gao, F.; Gao, F. Review of deep learning for photoacoustic imaging. Photoacoustics 2021, 21, 100215. [Google Scholar] [CrossRef] [PubMed]
- Antholzer, S.; Haltmeier, M.; Schwab, J. Deep learning for photoacoustic tomography from sparse data. Inverse Probl. Sci. Eng. 2019, 27, 987–1005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
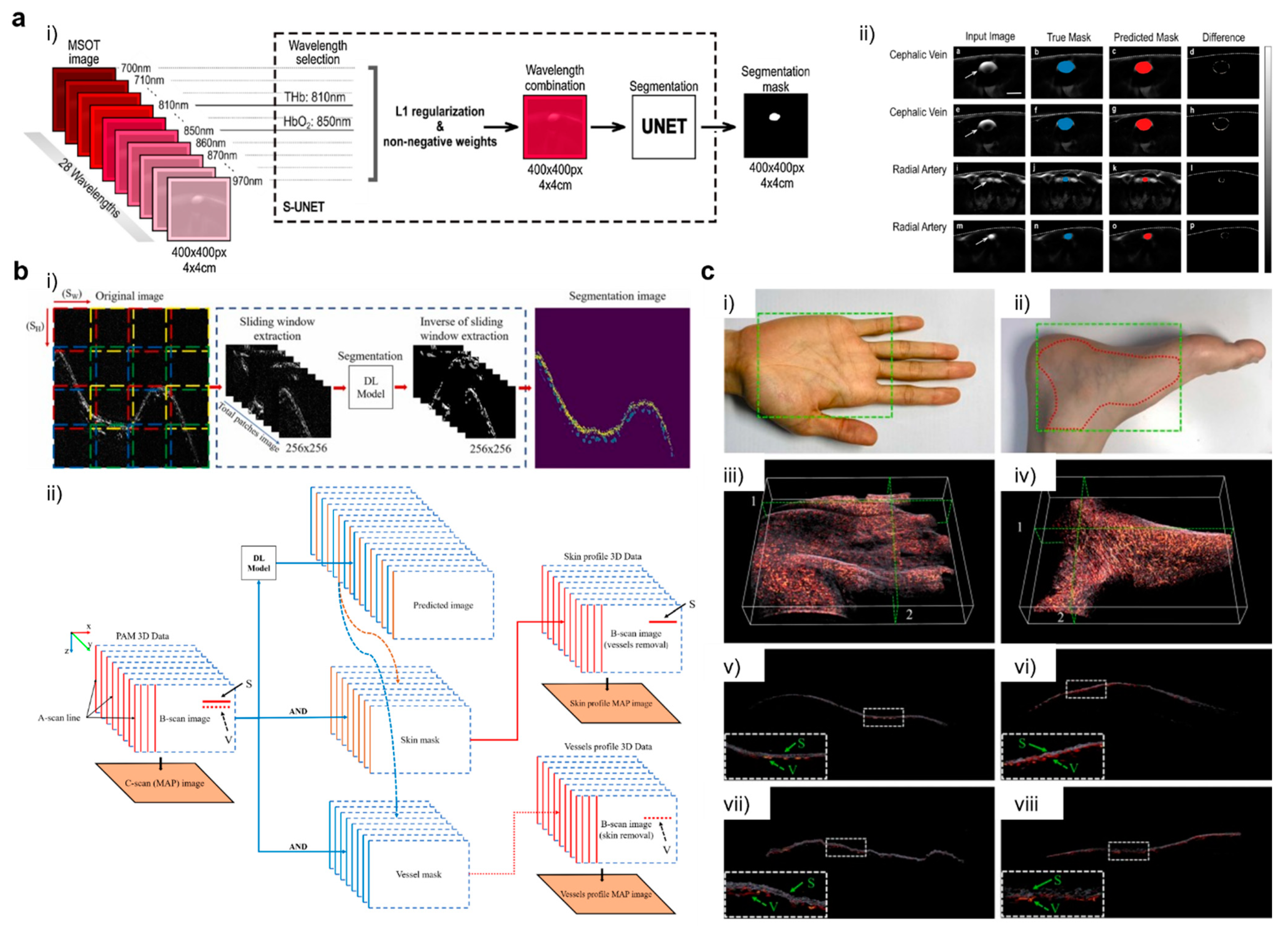
- Ly, C.D.; Nguyen, V.T.; Vo, T.H.; Mondal, S.; Park, S.; Choi, J.; Vu, T.T.H.; Kim, C.-S.; Oh, J. Full-view in vivo skin and blood vessels profile segmentation in photoacoustic imaging based on deep learning. Photoacoustics 2022, 25, 100310. [Google Scholar] [CrossRef] [PubMed]
- Singh, C. Medical Imaging using Deep Learning Models. Eur. J. Eng. Technol. Res. 2021, 6, 156–167. [Google Scholar] [CrossRef]
- Arakala, A.; Davis, S.; Horadam, K.J. Vascular Biometric Graph Comparison: Theory and Performance. In Handbook of Vascular Biometrics; Advances in Computer Vision and Pattern Recognition; Uhl, A., Busch, C., Marcel, S., Veldhuis, R., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 355–393. ISBN 978-3-030-27731-4. [Google Scholar]
- Semerád, L.; Drahanský, M. Retinal Vascular Characteristics. In Handbook of Vascular Biometrics; Advances in Computer Vision and Pattern Recognition; Uhl, A., Busch, C., Marcel, S., Veldhuis, R., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 309–354. ISBN 978-3-030-27731-4. [Google Scholar]
- Center for Devices and Radiological Health. Medical Imaging. Available online: https://www.fda.gov/radiation-emitting-products/radiation-emitting-products-and-procedures/medical-imaging (accessed on 17 December 2021).
- Ganguly, D.; Chakraborty, S.; Balitanas, M.; Kim, T. Medical Imaging: A Review. In Security-Enriched Urban Computing and Smart Grid; Kim, T., Stoica, A., Chang, R.-S., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 504–516. [Google Scholar]
- Cho, S.-G.; Jabin, Z.; Lee, C.; Bom, H.H.-S. The tools are ready, are we? J. Nucl. Cardiol. 2019, 26, 557–560. [Google Scholar] [CrossRef]
- Mamat, N.; Rahman, W.E.Z.W.A.; Soh, S.C.; Mahmud, R. Review methods for image segmentation from computed tomography images. In Proceedings of the AIP Conference Proceedings, Langkawi, Malaysia, 17 February 2015; Volume 1635, pp. 146–152. [Google Scholar] [CrossRef]
- Lenchik, L.; Heacock, L.; Weaver, A.A.; Boutin, R.D.; Cook, T.S.; Itri, J.; Filippi, C.G.; Gullapalli, R.P.; Lee, J.; Zagurovskaya, M.; et al. Automated Segmentation of Tissues Using CT and MRI: A Systematic Review. Acad. Radiol. 2019, 26, 1695–1706. [Google Scholar] [CrossRef]
- Reamaroon, N.; Sjoding, M.W.; Derksen, H.; Sabeti, E.; Gryak, J.; Barbaro, R.P.; Athey, B.D.; Najarian, K. Robust segmentation of lung in chest X-ray: Applications in analysis of acute respiratory distress syndrome. BMC Med. Imaging 2020, 20, 116. [Google Scholar] [CrossRef]
- Saad, M.N.; Muda, Z.; Ashaari, N.S.; Hamid, H.A. Image segmentation for lung region in chest X-ray images using edge detection and morphology. In Proceedings of the 2014 IEEE International Conference on Control System, Computing and Engineering (ICCSCE 2014), Penang, Malaysia, 28–30 November 2014; pp. 46–51. [Google Scholar]
- Cover, G.S.; Herrera, W.G.; Bento, M.P.; Appenzeller, S.; Rittner, L. Computational methods for corpus callosum segmentation on MRI: A systematic literature review. Comput. Methods Programs Biomed. 2018, 154, 25–35. [Google Scholar] [CrossRef]
- Gordillo, N.; Montseny, E.; Sobrevilla, P. State of the art survey on MRI brain tumor segmentation. Magn. Reson. Imaging 2013, 31, 1426–1438. [Google Scholar] [CrossRef]
- Helms, G. Segmentation of human brain using structural MRI. Magn. Reson. Mater. Phys. Biol. Med. 2016, 29, 111–124. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Kim, Y.; Zhou, L.; Plichta, K.; Allen, B.; Buatti, J.; Wu, X. Improving tumor co-segmentation on PET-CT images with 3D co-matting. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 224–227. [Google Scholar]
- Han, D.; Bayouth, J.; Song, Q.; Taurani, A.; Sonka, M.; Buatti, J.; Wu, X. Globally Optimal Tumor Segmentation in PET-CT Images: A Graph-Based Co-segmentation Method. In Information Processing in Medical Imaging; Székely, G., Hahn, H.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 245–256. [Google Scholar]
- Zhao, X.; Li, L.; Lu, W.; Tan, S. Tumor co-segmentation in PET/CT using multi-modality fully convolutional neural network. Phys. Med. Biol. 2018, 64, 15011. [Google Scholar] [CrossRef] [PubMed]
- Bass, V.; Mateos, J.; Rosado-Mendez, I.M.; Márquez, J. Ultrasound image segmentation methods: A review. AIP Conf. Proc. 2021, 2348, 50018. [Google Scholar] [CrossRef]
- Cheng, H.D.; Shan, J.; Ju, W.; Guo, Y.; Zhang, L. Automated breast cancer detection and classification using ultrasound images: A survey. Pattern Recognit. 2010, 43, 299–317. [Google Scholar] [CrossRef] [Green Version]
- Xian, M.; Zhang, Y.; Cheng, H.D.; Xu, F.; Zhang, B.; Ding, J. Automatic breast ultrasound image segmentation: A survey. Pattern Recognit. 2018, 79, 340–355. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Huang, Q.; Huang, X.; Hu, H.; Zeng, F.; Wang, W. Predicting Breast Cancer in Breast Imaging Reporting and Data System (BI-RADS) Ultrasound Category 4 or 5 Lesions: A Nomogram Combining Radiomics and BI-RADS. Sci. Rep. 2019, 9, 11921. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Chen, B.; Zhou, M.; Lan, H.; Gao, F. Photoacoustic Image Classification and Segmentation of Breast Cancer: A Feasibility Study. IEEE Access 2019, 7, 5457–5466. [Google Scholar] [CrossRef]
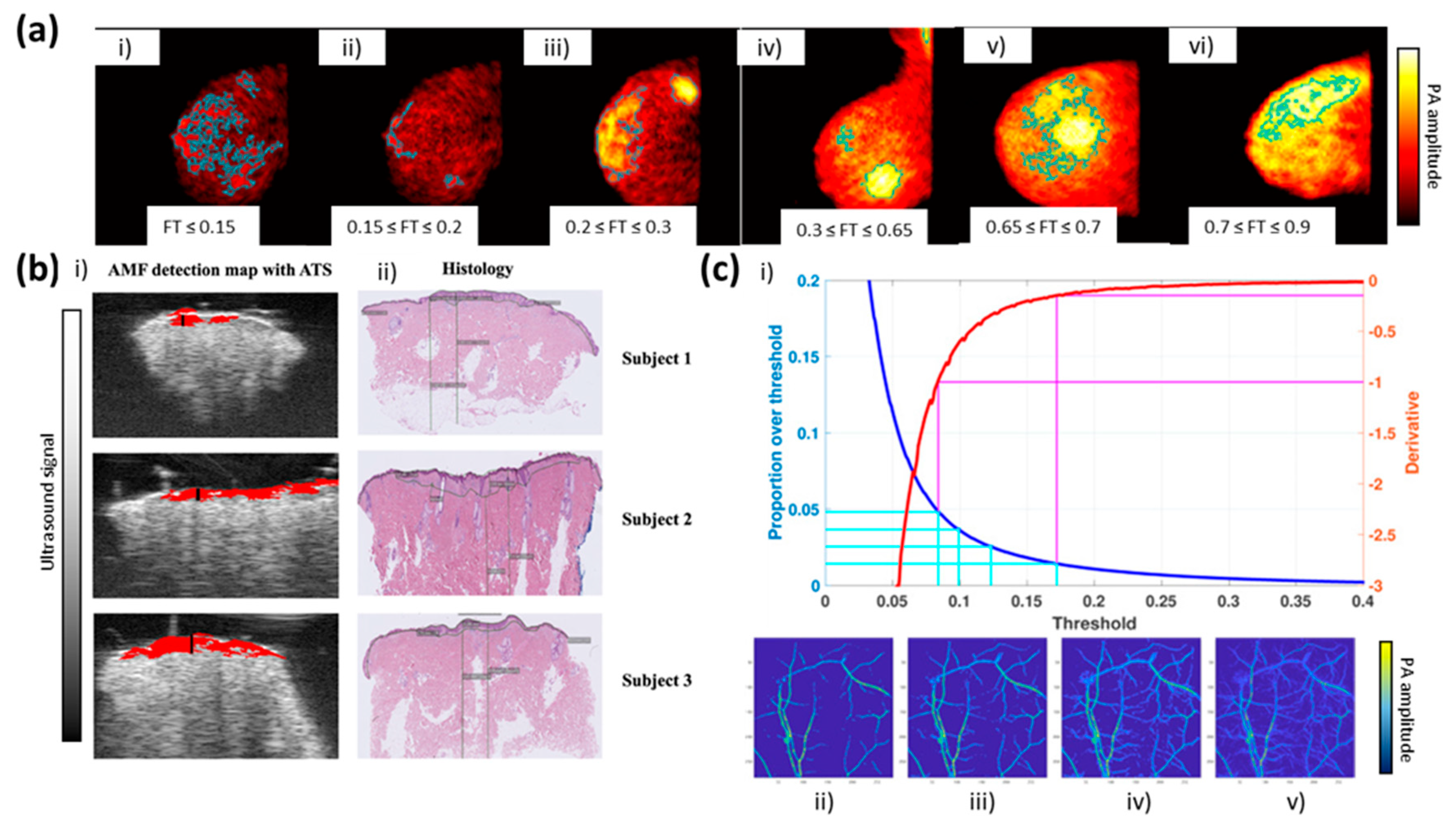
- Khodaverdi, A.; Erlöv, T.; Hult, J.; Reistad, N.; Pekar-Lukacs, A.; Albinsson, J.; Merdasa, A.; Sheikh, R.; Malmsjö, M.; Cinthio, M. Automatic threshold selection algorithm to distinguish a tissue chromophore from the background in photoacoustic imaging. Biomed. Opt. Express 2021, 12, 3836–3850. [Google Scholar] [CrossRef]
- Raumonen, P.; Tarvainen, T. Segmentation of vessel structures from photoacoustic images with reliability assessment. Biomed. Opt. Express 2018, 9, 2887–2904. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Chen, J.; Yao, J.; Lin, R.; Meng, J.; Liu, C.; Yang, J.; Li, X.; Wang, L.; Song, L. Multi-parametric quantitative microvascular imaging with optical-resolution photoacoustic microscopy in vivo. Opt. Express 2014, 22, 1500–1511. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Wang, G.; Lin, R.; Gong, X.; Song, L.; Li, T.; Wang, W.; Zhang, K.; Qian, X.; Zhang, H.; et al. Three-dimensional Hessian matrix-based quantitative vascular imaging of rat iris with optical-resolution photoacoustic microscopy in vivo. J. Biomed. Opt. 2018, 23, 46006. [Google Scholar] [CrossRef]
- Sun, M.; Li, C.; Chen, N.; Zhao, H.; Ma, L.; Liu, C.; Shen, Y.; Lin, R.; Gong, X. Full three-dimensional segmentation and quantification of tumor vessels for photoacoustic images. Photoacoustics 2020, 20, 100212. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, E.A.; Graham, C.A.; Lediju Bell, M.A. Acoustic Frequency-Based Approach for Identification of Photoacoustic Surgical Biomarkers. Front. Photonics 2021, 2, 6. [Google Scholar] [CrossRef]
- Cao, Y.; Kole, A.; Lan, L.; Wang, P.; Hui, J.; Sturek, M.; Cheng, J.-X. Spectral analysis assisted photoacoustic imaging for lipid composition differentiation. Photoacoustics 2017, 7, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Moore, M.J.; Hysi, E.; Fadhel, M.N.; El-Rass, S.; Xiao, Y.; Wen, X.-Y.; Kolios, M.C. Photoacoustic F-Mode imaging for scale specific contrast in biological systems. Commun. Phys. 2019, 2, 30. [Google Scholar] [CrossRef]
- Weszka, J.S.; Nagel, R.N.; Rosenfeld, A. A Threshold Selection Technique. IEEE Trans. Comput. 1974, 100, 1322–1326. [Google Scholar] [CrossRef]
- Abdallah, Y.M.Y.; Alqahtani, T. Research in Medical Imaging Using Image Processing Techniques; Medical Imaging—Principles and Applications; IntechOpen: London, UK, 2019; ISBN 978-1-78923-872-3. [Google Scholar]
- Find Connected Components in Binary Image-MATLAB Bwconncomp. Available online: https://www.mathworks.com/help/images/ref/bwconncomp.html (accessed on 17 December 2021).
- Measure Properties of Image Regions-MATLAB Regionprops. Available online: https://www.mathworks.com/help/images/ref/regionprops.html (accessed on 17 December 2021).
- Find Abrupt Changes in Signal-MATLAB Findchangepts. Available online: https://www.mathworks.com/help/signal/ref/findchangepts.html (accessed on 17 December 2021).
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Cao, R.; Li, J.; Kharel, Y.; Zhang, C.; Morris, E.; Santos, W.L.; Lynch, K.R.; Zuo, Z.; Hu, S. Photoacoustic microscopy reveals the hemodynamic basis of sphingosine 1-phosphate-induced neuroprotection against ischemic stroke. Theranostics 2018, 8, 6111–6120. [Google Scholar] [CrossRef]
- Meyer, F.; Beucher, S. Morphological segmentation. J. Vis. Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
- Frangi, A.F.; Niessen, W.J.; Vincken, K.L.; Viergever, M.A. Multiscale vessel enhancement filtering. In Medical Image Computing and Computer-Assisted Intervention—MICCAI’98; Wells, W.M., Colchester, A., Delp, S., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 130–137. [Google Scholar]
- Parikh, A.H.; Smith, J.K.; Ewend, M.G.; Bullitt, E. Correlation of MR Perfusion Imaging and Vessel Tortuosity Parameters in Assessment of Intracranial Neoplasms. Technol. Cancer Res. Treat. 2004, 3, 585–590. [Google Scholar] [CrossRef] [Green Version]
- Bullitt, E.; Gerig, G.; Pizer, S.M.; Lin, W.; Aylward, S.R. Measuring tortuosity of the intracerebral vasculature from MRA images. IEEE Trans. Med. Imaging 2003, 22, 1163–1171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baddour, N. Theory and analysis of frequency-domain photoacoustic tomography. J. Acoust. Soc. Am. 2008, 123, 2577–2590. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Wang, L. Incorporating spatial information in spectral unmixing: A review. Remote Sens. Environ. 2014, 149, 70–87. [Google Scholar] [CrossRef]
- Nondestructive Evaluation Techniques: Ultrasound. Available online: https://www.nde-ed.org/NDETechniques/Ultrasonics/EquipmentTrans/piezotransducers.xhtml (accessed on 17 December 2021).
- Press, W.; Teukolsky, S.; Vetterling, W.; Flannery, B. Gaussian mixture models and k-means clustering. In Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007; Volume 843, p. 846. [Google Scholar]
- Suganyadevi, S.; Seethalakshmi, V.; Balasamy, K. A review on deep learning in medical image analysis. Int. J. Multimed. Inf. Retr. 2021, 11, 19–38. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, R.; Sounderajah, V.; Martin, G.; Ting, D.S.W.; Karthikesalingam, A.; King, D.; Ashrafian, H.; Darzi, A. Diagnostic accuracy of deep learning in medical imaging: A systematic review and meta-analysis. NPJ Digit. Med. 2021, 4, 65. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2012; Volume 25. [Google Scholar]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Anaya-Isaza, A.; Mera-Jiménez, L.; Zequera-Diaz, M. An overview of deep learning in medical imaging. Inform. Med. Unlocked 2021, 26, 100723. [Google Scholar] [CrossRef]
- Huang, S.-C.; Pareek, A.; Seyyedi, S.; Banerjee, I.; Lungren, M.P. Fusion of medical imaging and electronic health records using deep learning: A systematic review and implementation guidelines. NPJ Digit. Med. 2020, 3, 136. [Google Scholar] [CrossRef]
- Zhou, S.K.; Greenspan, H.; Davatzikos, C.; Duncan, J.S.; Van Ginneken, B.; Madabhushi, A.; Prince, J.L.; Rueckert, D.; Summers, R.M. A Review of Deep Learning in Medical Imaging: Imaging Traits, Technology Trends, Case Studies With Progress Highlights, and Future Promises. Proc. IEEE 2021, 109, 820–838. [Google Scholar] [CrossRef]
- Liu, X.; Gao, K.; Liu, B.; Pan, C.; Liang, K.; Yan, L.; Ma, J.; He, F.; Zhang, S.; Pan, S.; et al. Advances in Deep Learning-Based Medical Image Analysis. Health Data Sci. 2021, 2021, 8786793. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, C.; Zhang, J.; Wang, Y.; Gao, F.; Gao, F. Human Breast Numerical Model Generation Based on Deep Learning for Photoacoustic Imaging. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 1919–1922. [Google Scholar]
- Chlis, N.-K.; Karlas, A.; Fasoula, N.-A.; Kallmayer, M.; Eckstein, H.-H.; Theis, F.J.; Ntziachristos, V.; Marr, C. A sparse deep learning approach for automatic segmentation of human vasculature in multispectral optoacoustic tomography. Photoacoustics 2020, 20, 100203. [Google Scholar] [CrossRef] [PubMed]
- Yuan, A.Y.; Yuan, A.Y.; Gao, Y.; Gao, Y.; Peng, L.; Zhou, L.; Zhou, L.; Zhou, L.; Liu, J.; Liu, J.; et al. Hybrid deep learning network for vascular segmentation in photoacoustic imaging. Biomed. Opt. Express 2020, 11, 6445–6457. [Google Scholar] [CrossRef] [PubMed]
- Gröhl, J.; Kirchner, T.; Adler, T.J.; Hacker, L.; Holzwarth, N.; Hernández-Aguilera, A.; Herrera, M.A.; Santos, E.; Bohndiek, S.E.; Maier-Hein, L. Learned spectral decoloring enables photoacoustic oximetry. Sci. Rep. 2021, 11, 6565. [Google Scholar] [CrossRef] [PubMed]
- Luke, G.P.; Hoffer-Hawlik, K.; Van Namen, A.C.; Shang, R. O-Net: A Convolutional Neural Network for Quantitative Photoacoustic Image Segmentation and Oximetry. arXiv 2019, arXiv:1911.01935. [Google Scholar]
- Ntziachristos, V.; Razansky, D. Molecular Imaging by Means of Multispectral Optoacoustic Tomography (MSOT). Chem. Rev. 2010, 110, 2783–2794. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Li, M.; Tang, Y.; Yao, J. Photoacoustic tomography of blood oxygenation: A mini review. Photoacoustics 2018, 10, 65–73. [Google Scholar] [CrossRef]
- Taruttis, A.; Ntziachristos, V. Advances in real-time multispectral optoacoustic imaging and its applications. Nat. Photonics 2015, 9, 219–227. [Google Scholar] [CrossRef]
- Choi, W.; Park, E.-Y.; Jeon, S.; Kim, C. Clinical photoacoustic imaging platforms. Biomed. Eng. Lett. 2018, 8, 139–155. [Google Scholar] [CrossRef]
- Steinberg, I.; Huland, D.M.; Vermesh, O.; Frostig, H.E.; Tummers, W.S.; Gambhir, S.S. Photoacoustic clinical imaging. Photoacoustics 2019, 14, 77–98. [Google Scholar] [CrossRef]
- Attia, A.B.E.; Balasundaram, G.; Moothanchery, M.; Dinish, U.S.; Bi, R.; Ntziachristos, V.; Olivo, M. A review of clinical photoacoustic imaging: Current and future trends. Photoacoustics 2019, 16, 100144. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, R. Legal and human rights issues of AI: Gaps, challenges and vulnerabilities. J. Responsible Technol. 2020, 4, 100005. [Google Scholar] [CrossRef]



| Type | Description | Advantages | Disadvantages | Applications | Paper(s) |
|---|---|---|---|---|---|
| Thresholding segmentation | Based on a histogram of image intensity to detect bias | (1) Manual/adaptive flexibility (2) Simplest process | (1) Manual process (2) Cut-off weak signal mixed with noise | Leveling breast cancer Tissue chromophore measuring Micro-vessel mapping | [76,77,78,79] |
| Morphology segmentation | Based on the partitioning of image intensity into homogeneous regions or clusters | (1) Boundary region to separate background/target (2) Measurement of shape | (1) Complex algorithms (expensive computation systems) | Quantitative measurement of oxygenation Tracking/monitoring of vasculature Three-dimensional mapping | [46,47,80,81,82] |
| Wavelet-based frequency segmentation | Based on the frequency domain to determine the difference in absorption coefficient | (1) Consistent with the characteristics of wide-band ultrasound transducers (2) Measurement of quantitative coefficient | (1) Complex algorithms (expensive computation systems) | Blood vessel segmentation Enhanced visualization of biological cells | [83,84,85] |
| Type | Description | Advantages | Disadvantages | Application | Paper(s) |
|---|---|---|---|---|---|
| Supervised learning | Based on label observation in the training prediction model | (1) Classification and regression (2) Simplest learning process | (1) Manual process (2) Limited by current knowledge |
| [56,77,109,110] |
| Unsupervised learning | Desired decisions without specific or explicit sample instruction | (1) Clustering/anomaly detection without instruction. (2) Quantitative measurement with hidden features | (1) Poor accuracy |
| [111,112,113] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.D.; Kwon, S.-Y.; Lee, C. Segmentation and Quantitative Analysis of Photoacoustic Imaging: A Review. Photonics 2022, 9, 176. https://doi.org/10.3390/photonics9030176
Le TD, Kwon S-Y, Lee C. Segmentation and Quantitative Analysis of Photoacoustic Imaging: A Review. Photonics. 2022; 9(3):176. https://doi.org/10.3390/photonics9030176
Chicago/Turabian StyleLe, Thanh Dat, Seong-Young Kwon, and Changho Lee. 2022. "Segmentation and Quantitative Analysis of Photoacoustic Imaging: A Review" Photonics 9, no. 3: 176. https://doi.org/10.3390/photonics9030176
APA StyleLe, T. D., Kwon, S.-Y., & Lee, C. (2022). Segmentation and Quantitative Analysis of Photoacoustic Imaging: A Review. Photonics, 9(3), 176. https://doi.org/10.3390/photonics9030176






