Analysis and Simulation of the Optical Properties of a Quantum Dot on a Graphene Nanoribbon System
Abstract
:1. Introduction
2. Theoretical Formulation
2.1. Plasma Frequency and Surface Plasmons Polarization of Graphene
2.2. Interaction between the Graphene Nanoribbon and the Quantum Dot
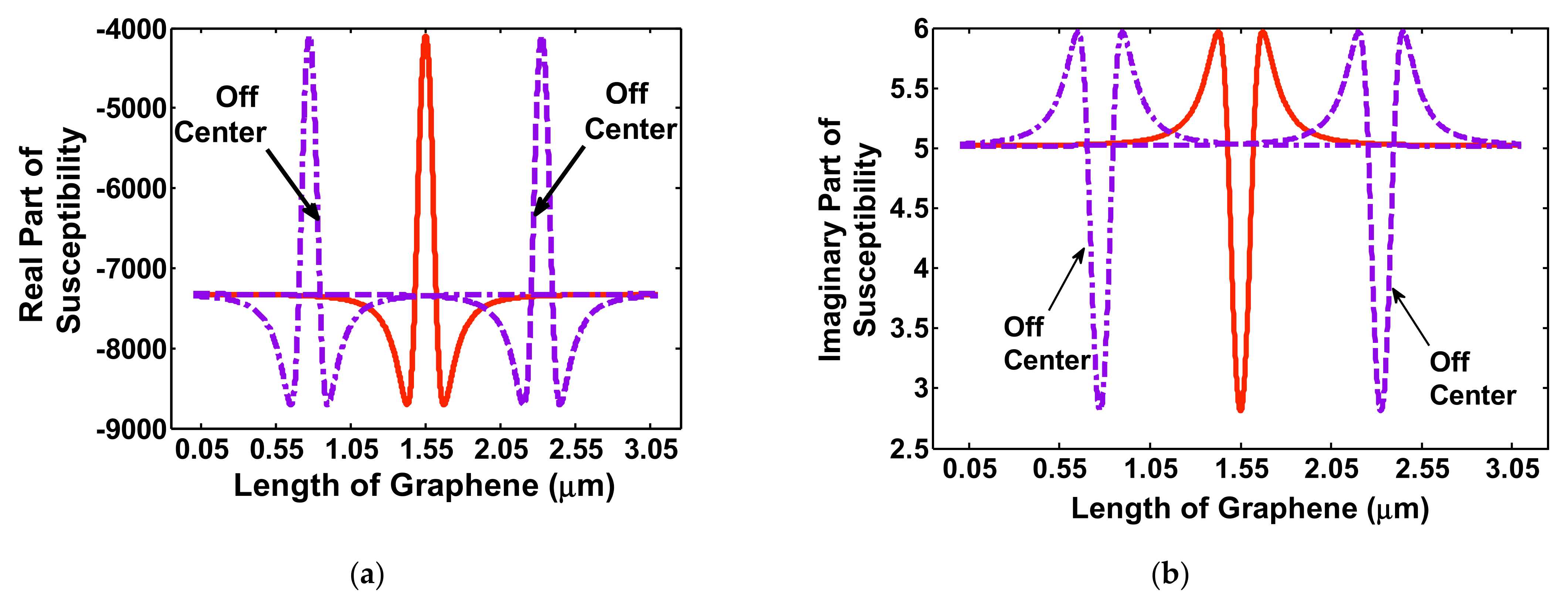
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bozhevolnyi, S.I.; Martin-Moreno, L.; Garcia-Vidal, F. Quantum Plasmonics; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Luther, J.; Jain, P.; Ewers, T.; Alivisatos, P. Localized surface plasmon resonances arising from free carriers in doped quantum dots. Nat. Mater. 2011, 10, 361–366. [Google Scholar] [CrossRef]
- Sadeghi, S.M.; Deng, L.; Li, X.; Huang, W.P. Plasmonic (thermal) electromagnetically induced transparency in metallic nanoparticle–quantum dot hybrid systems. Nanotechnology 2009, 20, 365401. [Google Scholar] [CrossRef]
- Artuso, R.D.; Bryant, G.W. Strongly coupled quantum dot-metal nanoparticle systems: Exciton-induced transparency, discontinuous response, and suppression as driven quantum oscillator effects. Phys. Rev. B 2010, 82, 195419. [Google Scholar] [CrossRef]
- Gubin, M.Y.; Prokhorov, A.V.; Volkov, V.S.; Evlyukhin, A.B. Controllable Excitation of Surface Plasmon Polaritons in Graphene-Based Semiconductor Quantum Dot Waveguides. Annalen Physik 2021, 533, 2100139. [Google Scholar] [CrossRef]
- Cox, J.D.; Singh, M.R.; Gumbs, G.; Anton, M.A.; Carreno, F. Dipole-dipole interaction between a quantum dot and a Graphene nanodisk. Phys. Rev. B 2012, 86, 125452. [Google Scholar] [CrossRef] [Green Version]
- Ogawa, S.; Fukushima, S.; Shimatani, M. Graphene Plasmonics in Sensor Applications: A Review. Sensors 2020, 20, 3563. [Google Scholar] [CrossRef] [PubMed]
- Plesco, I.; Dragoman, M.; Strobel, J.; Ghimpu, L.; Schütt, F.; Dinescu, A.; Ursaki, V.; Kienle, L.; Adelung, R.; Tiginyanu, I. Flexible pressure sensor based on Graphene aerogel microstructures functionalized with CdS nanocrystalline thin film. Superlattices Microstruct. 2018, 117, 418–422. [Google Scholar] [CrossRef]
- Armaghani, S.; Khani, S.; Danaei, M. Design of all-optical Graphene switches based on a Mach-Zehnder interferometer employing optical Kerr effect. Superlattices Microstruct. 2019, 135, 106244. [Google Scholar] [CrossRef]
- Kimmitt, N.; Wertz, E.A. Tracking the Coupling of Single Emitters to Plasmonic Nanoantennas with Single-Molecule Super-Resolution Imaging. ACS Photonics 2021, 8, 1020–1026. [Google Scholar] [CrossRef]
- Kok, P.; Lovett, B.W. Introduction to Optical Quantum Information Processing; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gonzalez-Tudela, A.; Cano, D.M.; Moreno, E.; Martín-Moreno, L.; Tejedor, C.; Garcia-Vidal, F.J. Entanglement of two qubits mediated by one-dimensional plasmonic waveguides. Phys. Rev. Lett. 2011, 106, 020501. [Google Scholar] [CrossRef]
- Kawata, S. Plasmonics: Future outlook. Jpn. J. Appl. Phys. 2012, 52, 010001. [Google Scholar] [CrossRef] [Green Version]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2007; Volume 1. [Google Scholar]
- West, P.; Ishii, S.; Naik, G.; Emani, N.K.; Shalaev, V.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Martinez, A.; Wang, F. Optical modulators with 2D layered materials. Nat. Photonics 2016, 10, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Wu, L.; Gao, F.; Luo, Y.; Zhang, B. Spoof plasmonics: From metamaterial concept to topological description. Adv. Mater. 2018, 30, 1706683. [Google Scholar] [CrossRef]
- Luo, X. Engineering optics 2.0: A revolution in optical materials, devices, and systems. ACS Photonics 2018, 5, 4724–4738. [Google Scholar] [CrossRef]
- Vakil, A. Transformation Optics Using Graphene: One-Atom-Thick Optical Devices Based on Graphene; University of Pennsylvania: Philadelphia, PA, USA, 2012. [Google Scholar]
- Wu, J.; Gong, M.; Schmitz, R.C.; Liu, B. Quantum Dot/Graphene Heterostructure Nanohybrid Photodetectors. In Quantum Dot Photodetectors; Springer: Berlin/Heidelberg, Germany, 2021; pp. 215–248. [Google Scholar]
- Vakil, A.; Engheta, N. Transformation optics using Graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [Green Version]
- Amirhosseini, A.A.; Safian, R. A hybrid plasmonic waveguide for the propagation of surface plasmon polariton at 1.55 μm on SOI substrate. IEEE Trans. Nanotechnol. 2013, 12, 1031–1036. [Google Scholar] [CrossRef]
- Ban, X.; Zhong, M.; Little, B.E. Broadband hybrid plasmonic Graphene modulator operating at mid-Infrared wavelength. Optik 2021, 247, 168036. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, X.; Ma, Z.; Cai, W.; Wang, L.; Xu, J. Surface plasmon modes in Graphene wedge and groove waveguides. Opt. Express 2013, 21, 32432–32440. [Google Scholar] [CrossRef]
- Gu, X.; Lin, I.-T.; Liu, J.-M. Extremely confined terahertz surface plasmon-polaritons in Graphene-metal structures. Appl. Phys. Lett. 2013, 103, 071103. [Google Scholar] [CrossRef]
- Gan, C.H.; Chu, H.S.; Li, E.P. Synthesis of highly confined surface plasmon modes with doped Graphene sheets in the midinfrared and terahertz frequencies. Phys. Rev. B 2012, 85, 125431. [Google Scholar] [CrossRef] [Green Version]
- Hosseininejad, S.E.; Komjani, N.; Noghani, M.T. A comparison of Graphene and noble metals as conductors for plasmonic one-dimensional waveguides. IEEE Trans. Nanotechnol. 2015, 14, 829–836. [Google Scholar] [CrossRef]
- Jovanović, V.B.; Radovic, I.; Borka, D.; Mišković, Z.L. High-energy plasmon spectroscopy of freestanding multilayer Graphene. Phys. Rev. B 2011, 84, 155416. [Google Scholar] [CrossRef] [Green Version]
- Engheta, N.; Ziolkowski, R.W. Metamaterials: Physics and Engineering Explorations; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Siahsar, M.; Jabbarzadeh, F.; Dolatyari, M.; Rostami, G.; Rostami, A. Fabrication of highly sensitive and Fast Response MIR Photodetector based on a New Hybrid Graphene Structure. Sens. Actuators A Phys. 2016, 238, 150–157. [Google Scholar] [CrossRef]
- Georgakilas, V.; Tiwari, J.N.; Kemp, K.C.; Perman, J.A.; Bourlinos, A.B.; Kim, K.S.; Zboril, R. Noncovalent functionalization of graphene and graphene oxide for energy materials, biosensing, catalytic, and biomedical applications. Chem. Rev. 2016, 116, 5464–5519. [Google Scholar] [CrossRef] [Green Version]
- Low, S.; Shon, Y.S. Molecular interactions between preformed metal nanoparticles and graphene families. Adv. Nano Res. 2018, 6, 357–375. [Google Scholar]
- Kuila, T.; Bose, S.; Mishra, A.K.; Khanra, P.; Kim, N.H.; Lee, J.H. Chemical functionalization of graphene and its applications. Prog. Mater. Sci. 2012, 57, 1061–1105. [Google Scholar] [CrossRef]
- Lu, Y.H.; Chen, W.; Feng, Y.P.; He, P.M. Tuning the Electronic Structure of Graphene by an Organic Molecule. J. Phys. Chem. B 2009, 113, 2–5. [Google Scholar] [CrossRef] [Green Version]

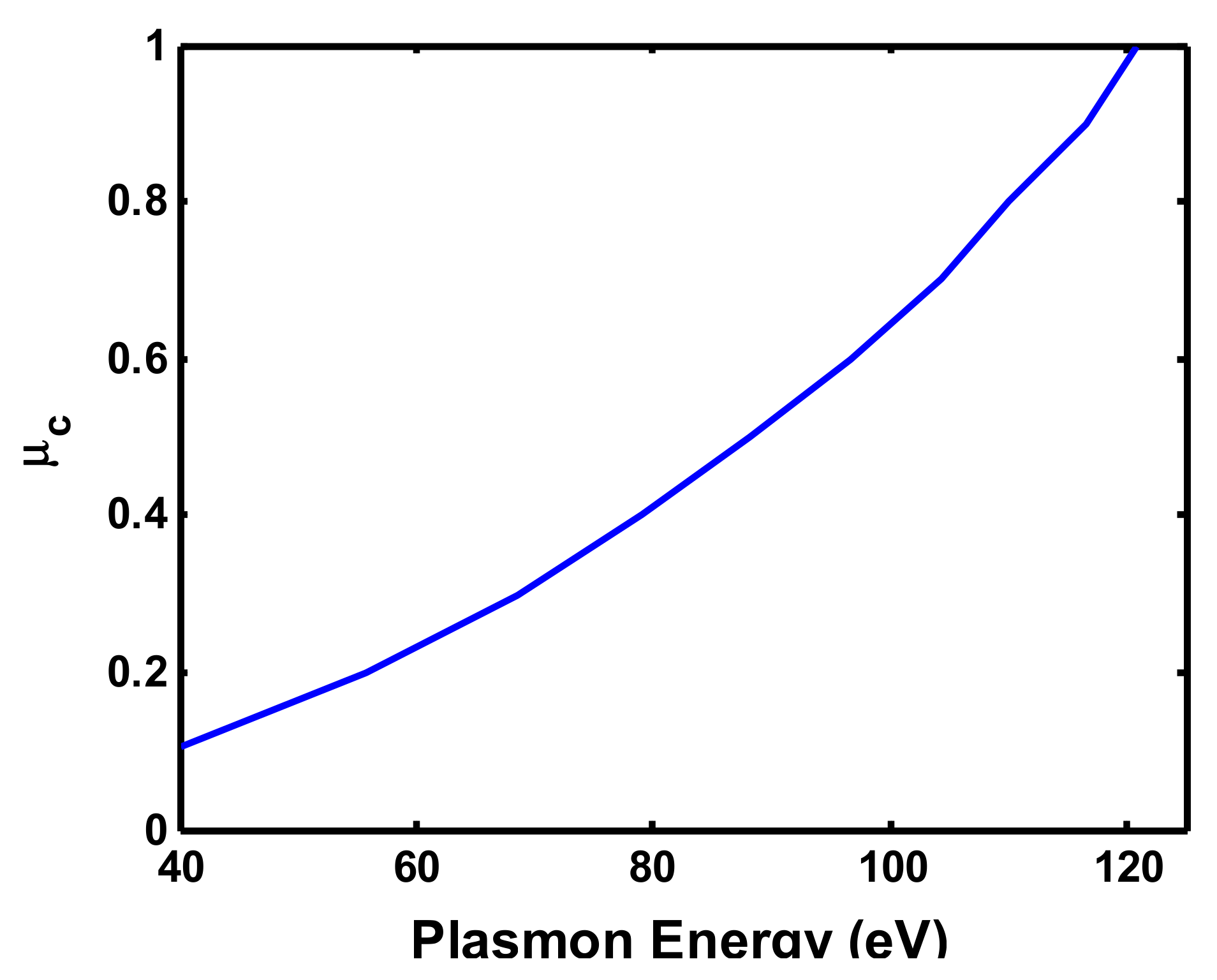




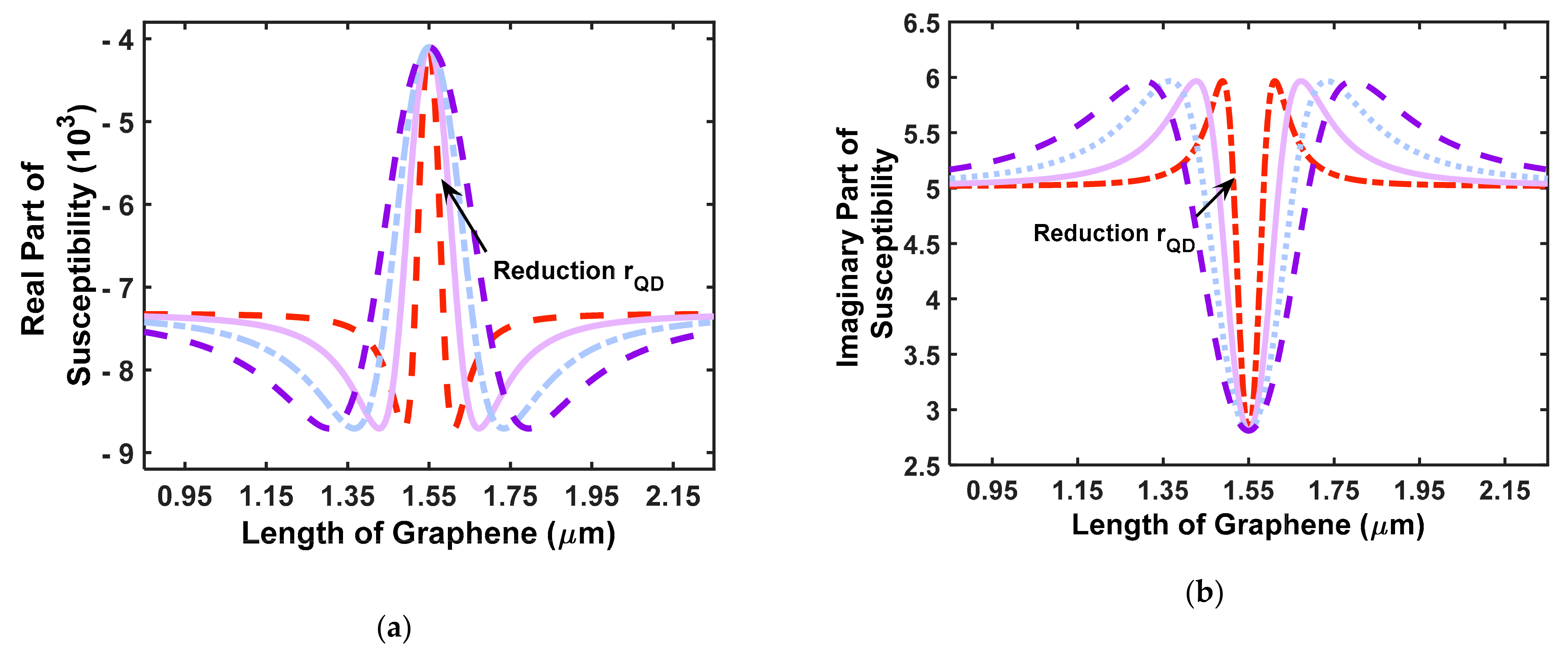
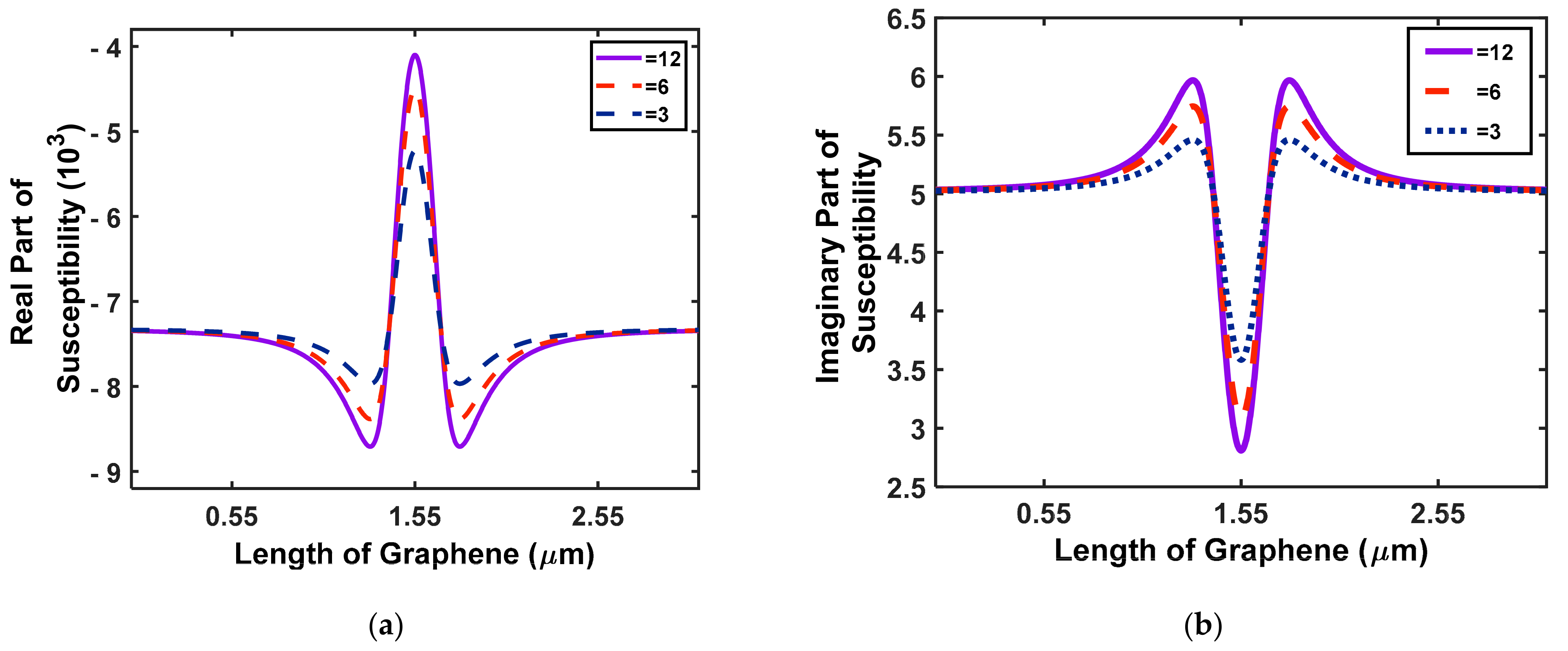
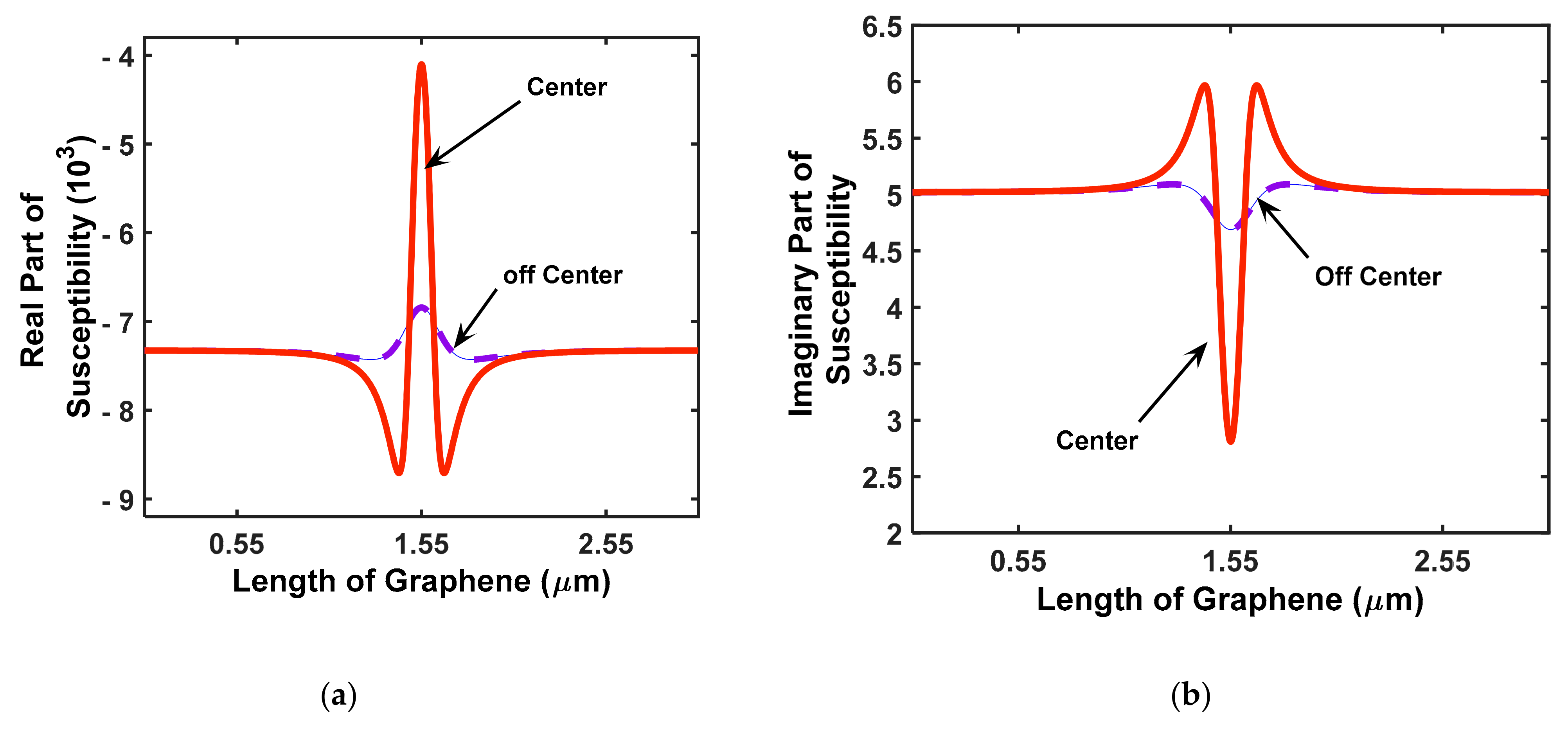
| Chemical Potential (eV) | Plasmon Energy (eV) |
|---|---|
| 0.2 | 55.87 |
| 0.4 | 88.22 |
| 0.6 | 104.4 |
| 0.8 | 110 |
| 1 | 121 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Armaghani, S.; Rostami, A.; Mirtaheri, P. Analysis and Simulation of the Optical Properties of a Quantum Dot on a Graphene Nanoribbon System. Photonics 2022, 9, 220. https://doi.org/10.3390/photonics9040220
Armaghani S, Rostami A, Mirtaheri P. Analysis and Simulation of the Optical Properties of a Quantum Dot on a Graphene Nanoribbon System. Photonics. 2022; 9(4):220. https://doi.org/10.3390/photonics9040220
Chicago/Turabian StyleArmaghani, Sahar, Ali Rostami, and Peyman Mirtaheri. 2022. "Analysis and Simulation of the Optical Properties of a Quantum Dot on a Graphene Nanoribbon System" Photonics 9, no. 4: 220. https://doi.org/10.3390/photonics9040220
APA StyleArmaghani, S., Rostami, A., & Mirtaheri, P. (2022). Analysis and Simulation of the Optical Properties of a Quantum Dot on a Graphene Nanoribbon System. Photonics, 9(4), 220. https://doi.org/10.3390/photonics9040220





