Real-Time Phase Retrieval Based on Cube-Corner Prisms Single Exposure
Abstract
:1. Introduction
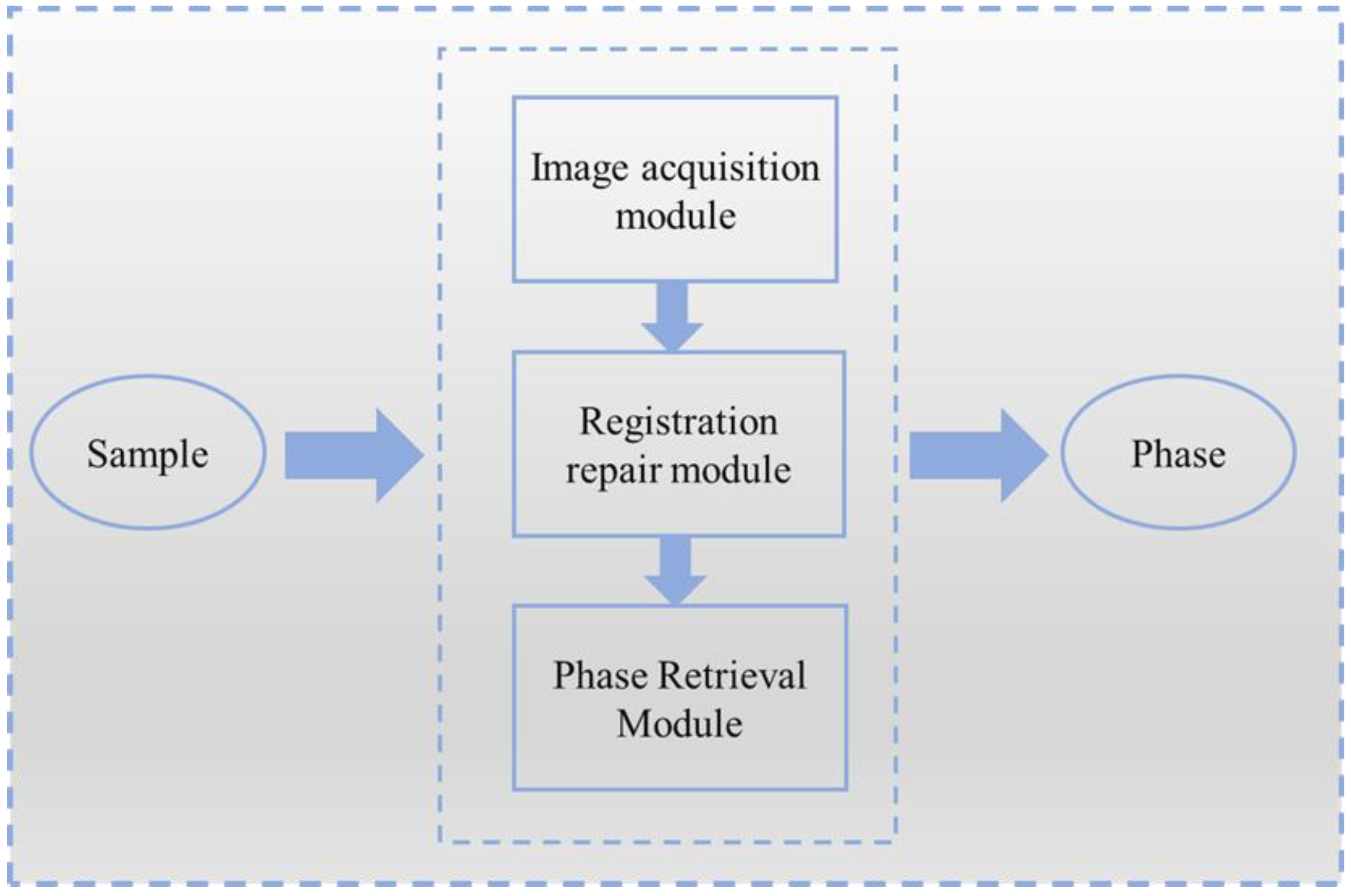
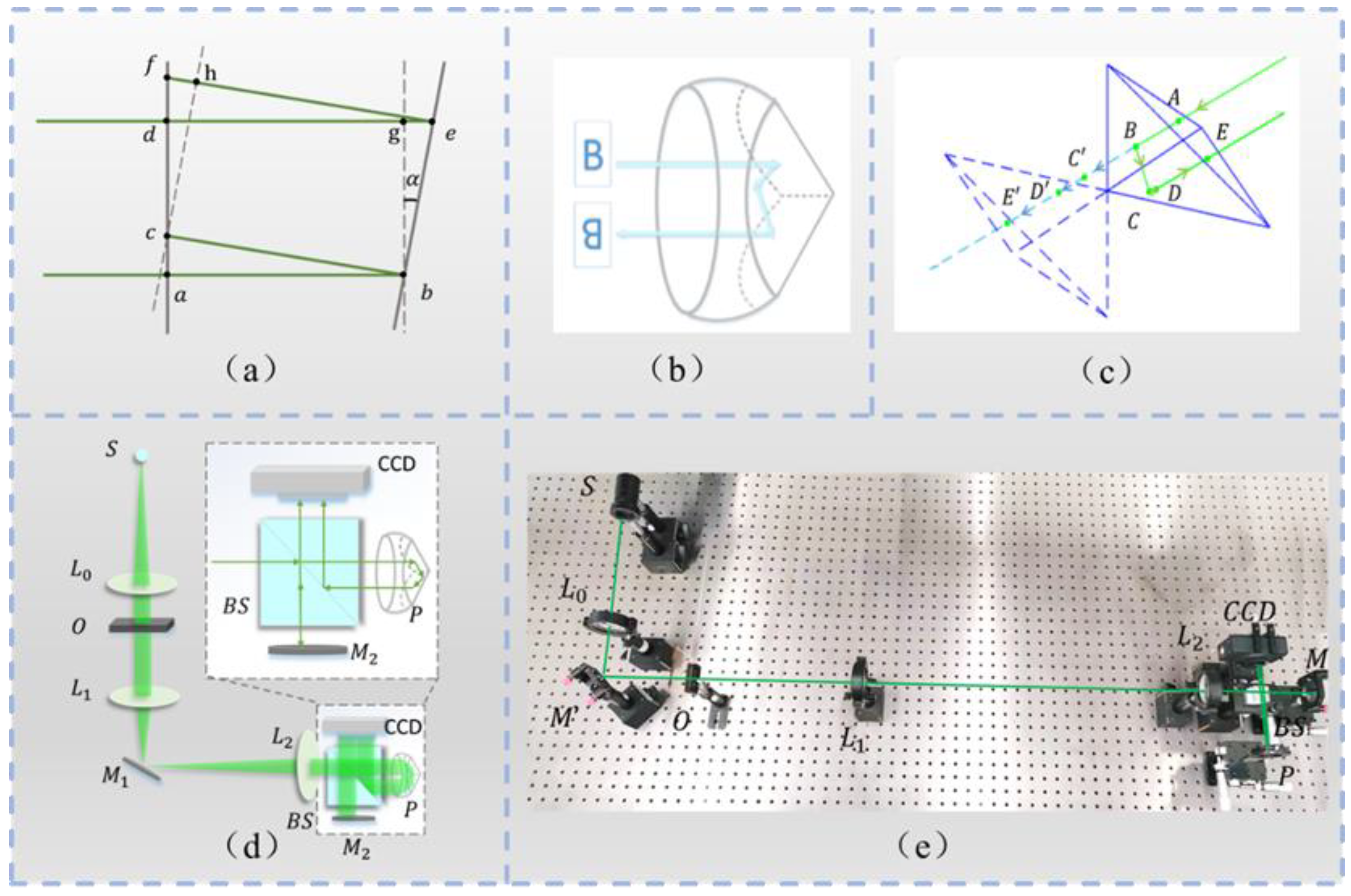
2. Phase Retrieval Imaging Technology Based on Cube-Corner Prisms
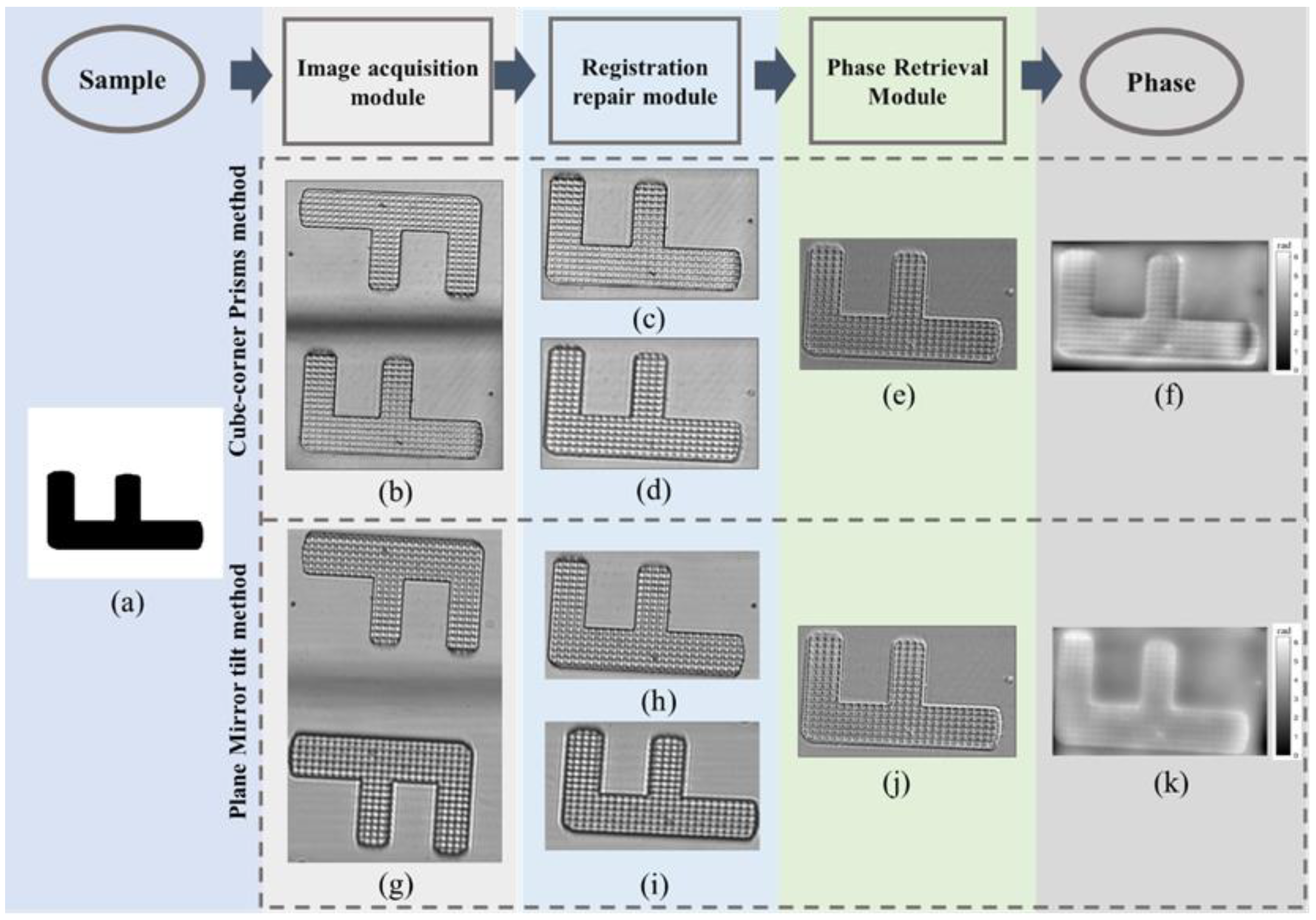
2.1. Image Acquisition Module
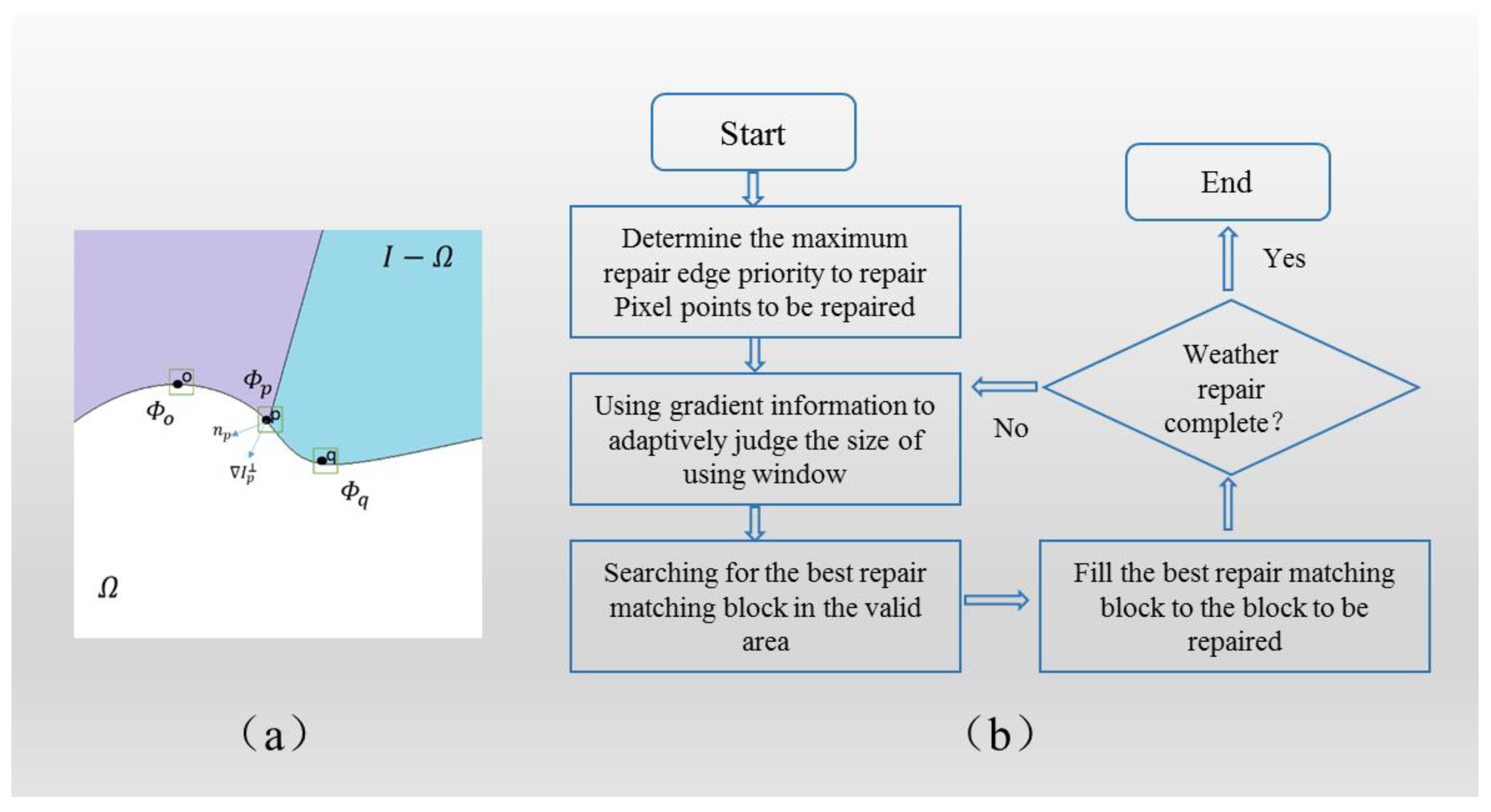
2.2. Registration Repair Module
2.2.1. Harris Corner Registration Algorithm
2.2.2. Fast Adaptive Repair Algorithm
2.2.3. Phase Retrieval Module
3. Experiment
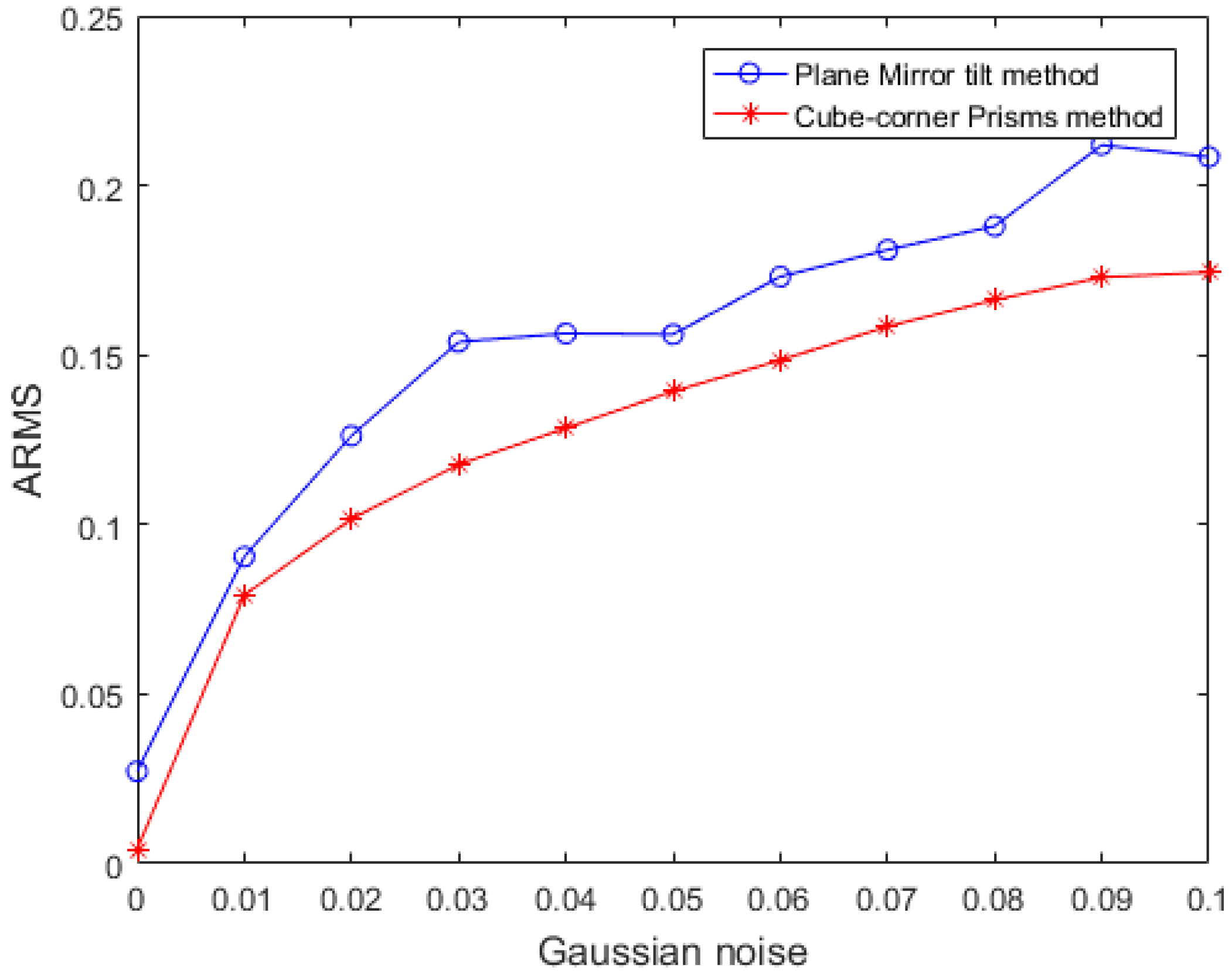
3.1. Simulation Experiment
3.2. Experimental Measurements
3.2.1. Qualitative Experiments Based on Lithography Samples
3.2.2. Quantitative Experiment Based on Micro-Lens Array
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Picazo-Bueno, J.A.; Trusiak, M.; Micó, V. Single-shot slightly off-axis digital holographic microscopy with add-on module based on beamsplitter cube. Opt. Express 2019, 27, 5655–5669. [Google Scholar] [CrossRef] [PubMed]
- Balasubramani, V.; Kujawińska, M.; Allier, C.; Anand, V.; Cheng, C.-J.; Depeursinge, C.; Hai, N.; Juodkazis, S.; Kalkman, J.; Kuś, A.; et al. Roadimage on digital holography-based quantitative phase imaging. J. Imaging 2021, 7, 252. [Google Scholar] [CrossRef] [PubMed]
- Konijnenberg, A.P.; Lu, X.; Liu, L.; Coene, W.M.; Zhao, C.; Urbach, H.P. Non-iterative method for phase retrieval and coherence characterization by focus variation using a fixed star-shaped mask. Opt. Express 2018, 26, 9332–9343. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anand, V.; Katkus, T.; Linklater, D.P.; Ivanova, E.P.; Juodkazis, S. Lensless three-dimensional quantitative phase imaging using phase retrieval algorithm. J. Imaging 2020, 6, 99. [Google Scholar] [CrossRef]
- Bai, H.; Min, R.; Yang, Z.; Zhu, F. Slightly off-axis flipping digital holography using a reflective grating. J. Opt. 2020, 22, 035602. [Google Scholar] [CrossRef]
- Teague, M.R. Deterministic phase retrieval: A Green’s function solution. JOSA 1983, 73, 1434–1441. [Google Scholar] [CrossRef]
- Estrada, J.C.; Marroquin, J.L.; Medina, O.M. Reconstruction of local frequencies for recovering the unwrapped phase in optical interferometry. Sci. Rep. 2017, 7, 6727. [Google Scholar] [CrossRef] [PubMed]
- Nugent, K.A.; Gureyev, T.E.; Cookson, D.F.; Paganin, D.; Barnea, Z.N. Quantitative phase imaging using hard x rays. Phys. Rev. Lett. 1996, 77, 2961. [Google Scholar] [CrossRef] [PubMed]
- Volkov, V.V.; Zhu, Y.; De Graef, M. A new symmetrized solution for phase retrieval using the transport of intensity equation. Micron 2002, 33, 411–416. [Google Scholar] [CrossRef]
- Mayo, S.C.; Davis, T.J.; Gureyev, T.E.; Miller, P.R.; Paganin, D.; Pogany, A.; Stevenson, A.W.; Wilkins, S.W. X-ray phase-contrast microscopy and microtomography. Opt. Express 2003, 11, 2289–2302. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Wang, J.; Shen, C.; Zhang, C.; Zhang, F.; Bao, W. Multiplicative Reconstruction Based on the Transport of Intensity Equation. In Fuzzy Systems and Data Mining IV; IOS Press: Amsterdam, The Netherlands, 2018; pp. 924–929. [Google Scholar]
- Zuo, C.; Li, J.; Sun, J.; Fan, Y.; Zhang, J.; Lu, L.; Zhang, R.; Wang, B.; Huang, L.; Chen, Q. Transport of intensity equation: A tutorial. Opt. Lasers Eng. 2020, 16, 106187. [Google Scholar] [CrossRef]
- Waller, L.; Kou, S.S.; Sheppard, C.J.; Barbastathis, G. Phase from chromatic aberrations. Opt. Express 2010, 18, 22817–22825. [Google Scholar] [CrossRef] [PubMed]
- Waller, L.; Luo, Y.; Yang, S.Y.; Barbastathis, G. Transport of intensity phase imaging in a volume holographic microscope. Opt. Lett. 2010, 35, 2961–2963. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Qu, W.; Asundi, A. Noninterferometric single-shot quantitative phase microscopy. Opt. Lett. 2013, 38, 3538–3541. [Google Scholar] [CrossRef]
- Kwon, H.; Arbabi, E.; Kamali, S.M.; Faraji-Dana, M.; Faraon, A. Computational complex optical field imaging using a designed metasurface diffuser. Optica 2018, 5, 924–931. [Google Scholar] [CrossRef]
- Kwon, H.; Arbabi, E.; Kamali, S.M.; Faraji-Dana, M.; Faraon, A. Single-shot quantitative phase gradient microscopy using a system of multifunctional metasurfaces. Nat. Photonics 2020, 14, 109–114. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A.K.; Nishchal, N.K. Single-shot transport of intensity equation based phase imaging using refractive index variation. In Digital Holography and Three-Dimensional Imaging; Optical Society of America: Bordeaux, France, 2019; p. M5B.7. [Google Scholar]
- Wang, K.; Di, J.; Li, Y.; Ren, Z.; Kemao, Q.; Zhao, J. Transport of intensity equation from a single intensity image via deep learning. Opt. Lasers Eng. 2020, 134, 106233. [Google Scholar] [CrossRef]
- Engay, E.; Huo, D.; Malureanu, R.; Bunea, A.-I.; Lavrinenko, A. Polarization-Dependent All-Dielectric Metasurface for Single-Shot Quantitative Phase Imaging. Nano Lett. 2021, 21, 3820–3826. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Di, J.; Ma, C.; Zhang, J.; Zhong, J.; Wang, K.; Xi, T.; Zhao, J. Quantitative phase microscopy for cellular dynamics based on transport of intensity equation. Opt. Express 2018, 26, 586–593. [Google Scholar] [CrossRef]
- Gupta, A.K.; Mahendra, R.; Nishchal, N.K. Single-shot phase imaging based on transport of intensity equation. Opt. Commun. 2020, 477, 126347. [Google Scholar] [CrossRef]
- Kuang, C.F.; Feng, Q.B.; Liu, X. Analysis of Reflection Property of Cube-corner retroreflector with Vector Expression. J. Appl. Opt. 2004, 25, 25–27. [Google Scholar]
- Zeng, Q.; Liu, L.; Li, J. Image registration method based on improved Harris corner detector. Chin. Opt. Lett. 2010, 8, 573–576. [Google Scholar] [CrossRef]
- Criminisi, A.; Pérez, P.; Toyama, K. Region filling and object removal by exemplar-based image inpainting. IEEE Trans. Image Processing 2004, 13, 1200–1212. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.M.; Zhang, F.; Song, Q.; Zhu, J. Application of Hybrid Iterative Algorithm in TIE Phase Retrieval with Large Defocusing Distance. J. Photonics 2016, 36, 912001. [Google Scholar]
- Allen, L.J.; Oxley, M.P. Phase retrieval from series of images obtained by defocus variation. Opt. Commun. 2001, 199, 65–75. [Google Scholar] [CrossRef]
- Fang, C.; Dai, B.; Zhuo, R.; Yuan, X.; Gao, X.; Wen, J.; Sheng, B.; Zhang, D. Focal-length-tunable elastomer-based liquid-filled plano–convex mini lens. Opt. Lett. 2016, 41, 404–407. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Lv, Q.; Wei, S.; Deng, H.; Gao, Y. Rapid phase retrieval using SLM based on transport of intensity equation. Infrared Laser Eng. 2018, 47, 0722003. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Q.; Sun, J.; Tian, L.; Zuo, C. On a universal solution to the transport-of-intensity equation. Opt. Lett. 2020, 45, 3649–3652. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Zhu, X.; Li, J.; Tian, Z. Real-Time Phase Retrieval Based on Cube-Corner Prisms Single Exposure. Photonics 2022, 9, 230. https://doi.org/10.3390/photonics9040230
Cheng H, Zhu X, Li J, Tian Z. Real-Time Phase Retrieval Based on Cube-Corner Prisms Single Exposure. Photonics. 2022; 9(4):230. https://doi.org/10.3390/photonics9040230
Chicago/Turabian StyleCheng, Hong, Xiaotian Zhu, Ju Li, and Zhengguang Tian. 2022. "Real-Time Phase Retrieval Based on Cube-Corner Prisms Single Exposure" Photonics 9, no. 4: 230. https://doi.org/10.3390/photonics9040230
APA StyleCheng, H., Zhu, X., Li, J., & Tian, Z. (2022). Real-Time Phase Retrieval Based on Cube-Corner Prisms Single Exposure. Photonics, 9(4), 230. https://doi.org/10.3390/photonics9040230



