Analyzing the Effects of a Basin on Atmospheric Environment Relevant to Optical Turbulence
Abstract
:1. Introduction
2. Experiments Details
3. Methodology of Estimating Optical Turbulence
3.1. Estimation Models
3.2. Integrated Astroclimatic Parameters
4. Results and Discussion
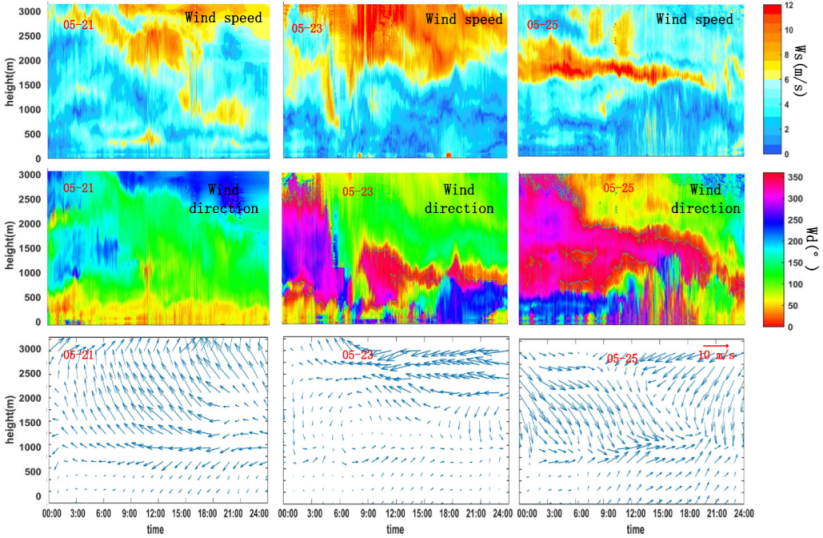
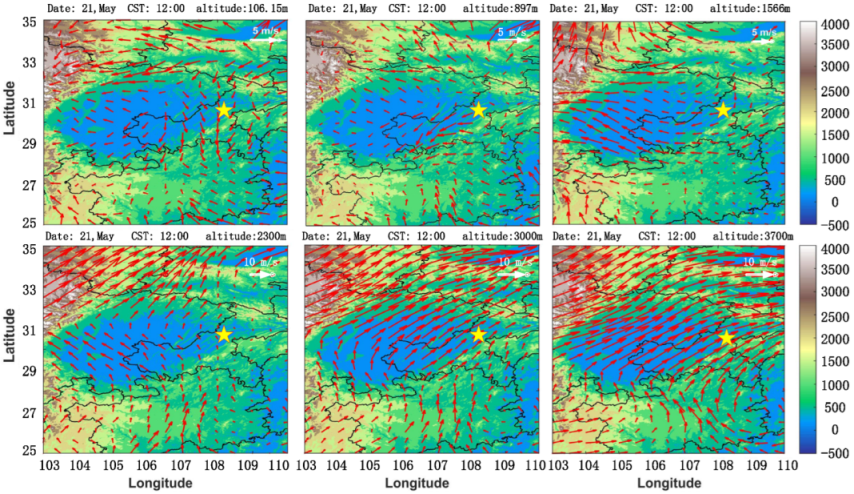
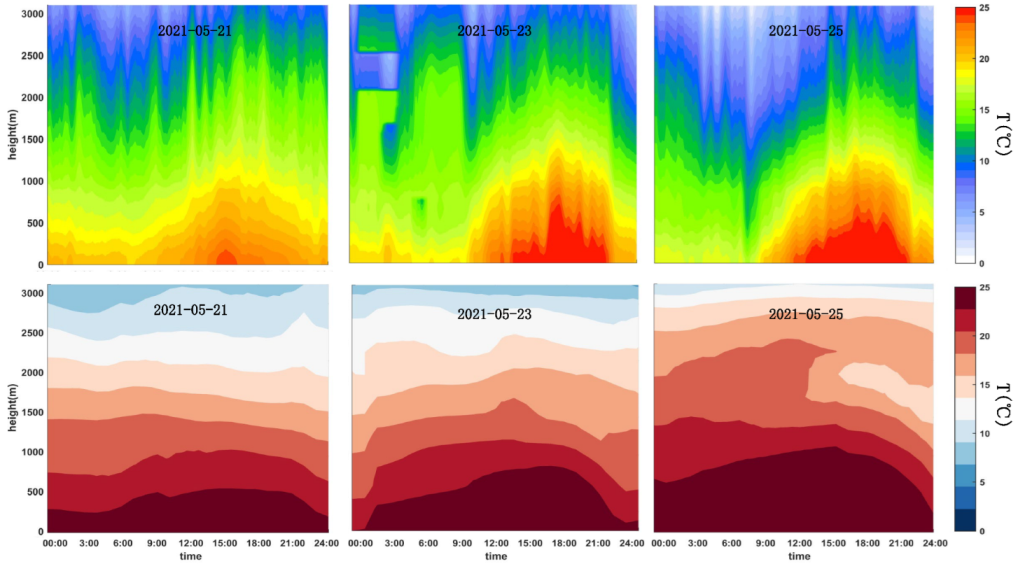
4.1. Characteristics of Basic Meteorological Parameters
4.2. Modification of HMNSP99 Outer Scale Model
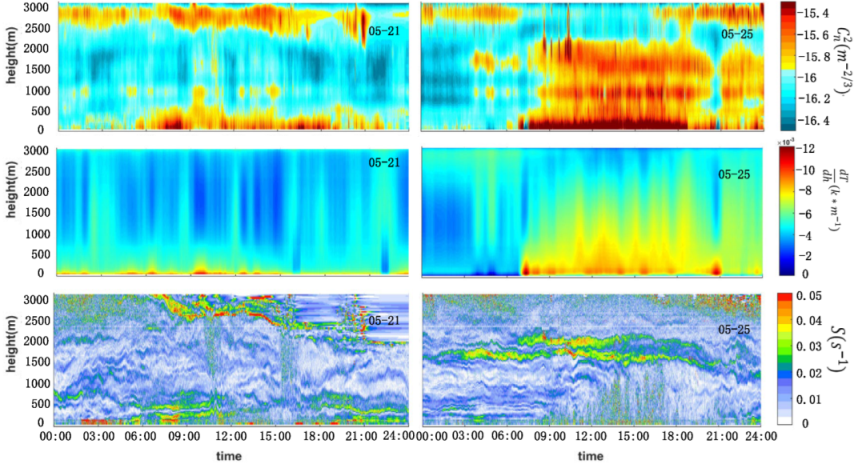
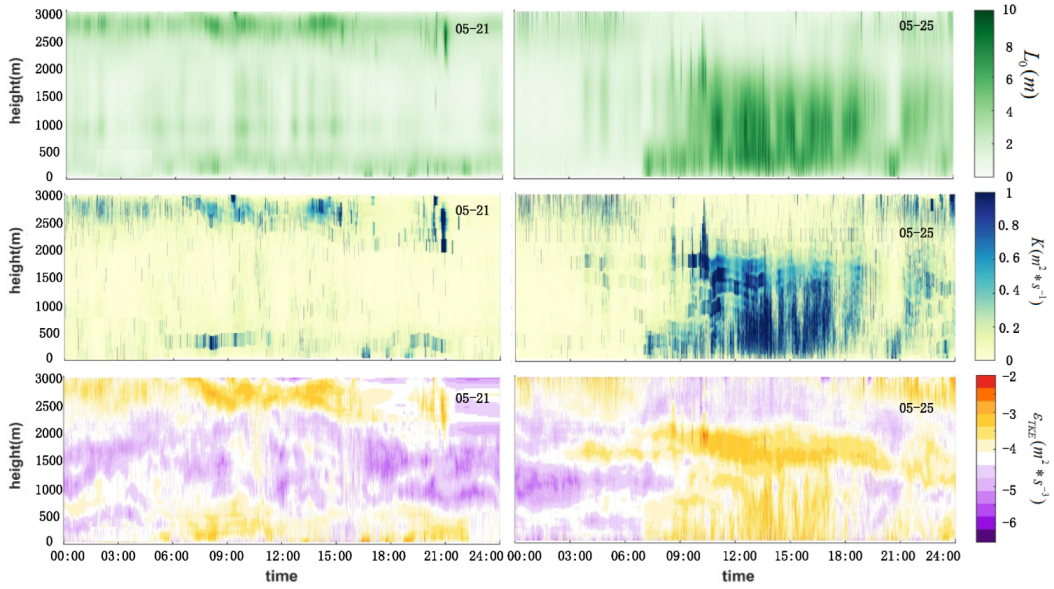
4.3. Spatiotemporal Characteristics and Effect Factors of Optical Turbulence
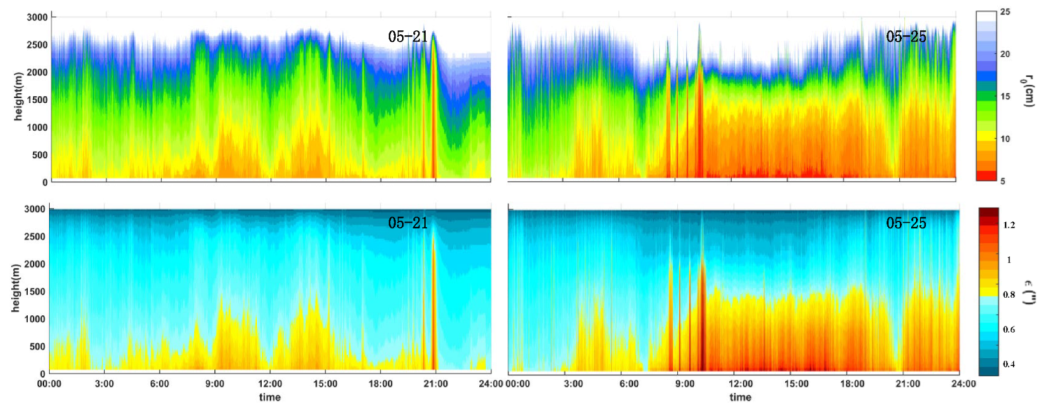
4.4. Spatiotemporal Characteristics of Turbulence Basic Parameters
4.5. Spatiotemporal Characteristics of Astronomical Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tatarski, V.I.; Silverman, R.A.; Chako, N. Wave Propagation in a Turbulent Medium. Phys. Today 1961, 14, 46. [Google Scholar] [CrossRef]
- Hutt, D.L. Modeling and measurement of atmospheric optical turbulence over land. Opt. Eng. 1999, 38, 1288–1295. [Google Scholar] [CrossRef]
- Roddier, F. V The Effects of Atmospheric Turbulence in Optical Astronomy. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 1981; Volume 19, pp. 281–376. [Google Scholar]
- Fried, D.L.; Mevers, G.E.; Keister, M.P. Measurements of Laser-Beam Scintillation in the Atmosphere. J. Opt. Soc. Am. 1967, 57, 787–797. [Google Scholar] [CrossRef]
- Scipión, D.E.; Lawrence, D.A.; Milla, M.A.; Woodman, R.F.; Lume, D.A.; Balsley, B.B. Simultaneous observations of structure function parameter of refractive index using a high-resolution radar and the DataHawk small airborne measurement system. Ann. Geophys. 2016, 34, 767–780. [Google Scholar] [CrossRef] [Green Version]
- Shao, S.; Qin, F.; Liu, Q.; Xu, M.; Cheng, X. Turbulent Structure Function Analysis Using Wireless Micro-Thermometer. IEEE Access 2020, 8, 123929–123937. [Google Scholar] [CrossRef]
- Xiaoqing, W.U.; Qiguo, T.; Peng, J.; Bo, C.; Qing, C.; Jun, C.A.I.; Xinmiao, J.I.N.; Hongyan, Z. A new method of measuring optical turbulence of atmospheric surface layer at Antarctic Taishan Station with ultrasonic anemometer. Adv. Polar Sci. 2015, 26, 305. [Google Scholar] [CrossRef]
- Vernin, J.; Barletti, R.; Ceppatelli, G.; Paternò, L.; Righini, A.; Speroni, N. Optical remote sensing of atmospheric turbulence: A comparison with simultaneous thermal measurements. Appl. Opt. 1979, 18, 243–247. [Google Scholar] [CrossRef] [PubMed]
- Anand, N.; Sunilkumar, K.; Satheesh, S.K.; Moorthy, K.K. Entanglement of near-surface optical turbulence to atmospheric boundary layer dynamics and particulate concentration: Implications for optical wireless communication systems. Appl. Opt. 2020, 59, 1471–1483. [Google Scholar] [CrossRef] [PubMed]
- Miller, M.; Zieske, P. Turbulence Environment Characterization; Interim Report; Avco-Everett Research Lab.: Everett, MA, USA, 1979; p. 135. [Google Scholar]
- Good, R.E.; Beland, R.R.; Murphy, E.A.; Brown, J.H.; Dewan, E.M. Atmospheric models of optical turbulence. Proc. SPIE 1988, 928, 165–186. [Google Scholar] [CrossRef]
- Jumper, G.; Beland, R. Progress in the understanding and modeling of atmospheric optical turbulence. In Proceedings of the 31st Plasmadynamics and Lasers Conference, Denver, CO, USA, 19–22 June 2000. [Google Scholar]
- Beland, R.R.; Brown, J.H. A deterministic temperature model for stratospheric optical turbulence. Phys. Scr. 1988, 37, 419–423. [Google Scholar] [CrossRef]
- Nath, D.; Venkat Ratnam, M.; Patra, A.K.; Krishna Murthy, B.V.; Bhaskar Rao, S.V. Turbulence characteristics over tropical station Gadanki (13.5°N, 79.2°E) estimated using high-resolution GPS radiosonde data. J. Geophys. Res. Atmos. 2010, 115, D07102. [Google Scholar] [CrossRef]
- Hufnagel, R.; Stanley, N. Modulation Transfer Function Associated with Image Transmission through Turbulent Media. JOSA 1964, 54, 52–60. [Google Scholar] [CrossRef]
- Warnock, J.M.; Vanzandt, T.E. A statistical model to estimate refractivity turbulence structure constant Cn2 in the free atmosphere. Int. Counc. Sci. Unions Middle Atmos. Program. Handb. MAP 1986, 20, 166. [Google Scholar]
- Abahamid, A.; Jabiri, A.; Vernin, J.; Zouhair, B.; Azouit, M.; Agabi, A. Optical turbulence modeling in the boundary layer and free atmosphere using instrumented meteorological balloons. Astron. Astrophys. 2004, 416, 1193–1200. [Google Scholar] [CrossRef] [Green Version]
- Bi, C.; Qian, X.; Liu, Q.; Zhu, W.; Li, X.; Luo, T.; Wu, X.; Qing, C. Estimating and measurement of atmospheric optical turbulence accordingto balloon-borne radiosonde for three sites in China. J. Opt. Soc. Am. A 2020, 37, 1785–1794. [Google Scholar] [CrossRef]
- Zhang, R.; Jing, J.; Tao, J.; Hsu, S.C.; Wang, G.; Cao, J.; Lee, C.S.L.; Zhu, L.; Chen, Z.; Zhao, Y.; et al. Chemical characterization and source apportionment of PM2.5 in Beijing: Seasonal perspective. Atmos. Chem. Phys. 2013, 13, 7053–7074. [Google Scholar] [CrossRef] [Green Version]
- Qing, C.; Wu, X.; Li, X.; Zhu, W. Performance analysis of weather research and forecasting model for simulating near-surface optical turbulence over land. Optik 2019, 188, 225–232. [Google Scholar] [CrossRef]
- Qing, C.; Wu, X.; Li, X.; Zhu, W.; Qiao, C.; Rao, R.; Mei, H. Use of weather research and forecasting model outputs to obtain near-surface refractive index structure constant over the ocean. Opt. Express 2016, 24, 13303–13315. [Google Scholar] [CrossRef]
- Shao, S.; Qin, F.; Xu, M.; Liu, Q.; Han, Y.; Xu, Z. Temporal and spatial variation of refractive index structure coefficient over South China sea. Results Eng. 2020, 9, 100191. [Google Scholar] [CrossRef]
- Su, C.; Wu, X.; Luo, T.; Wu, S.; Qing, C. Adaptive niche-genetic algorithm based on backpropagation neural network for atmospheric turbulence forecasting. Appl. Opt. 2020, 59, 3699–3705. [Google Scholar] [CrossRef]
- Beland, R.R. Propagation through atmospheric optical turbulence. In The Infrared and Electro-Optical Systems Handbook; Infrared Information Analysis Center: Ann Arbor, MI, USA, 1993; pp. 157–232. [Google Scholar]
- Bufton, J. Correlation of Microthermal Turbulence Data with Meteorological Soundings in the Troposphere. J. Atmos. Sci. 1973, 30, 83–87. [Google Scholar] [CrossRef]
- Dewan, E.; Good, R.; Beland, R.; Brown, J. A Model for Cn(2) (Optical Turbulence) Profiles Using Radiosonde Data; Directorate of Geophysics, Air Force Materiel Command: MA, USA, 1993; p. 50. Available online: https://www.semanticscholar.org/paper/A-Model-for-Csubn(2)-(Optical-Turbulence)-Profiles-Dewan-Good/b202d31abb56ab8af7810f1c26d9135e436d46b8 (accessed on 16 February 2022).
- Han, Y.; Wu, X.; Luo, T.; Qing, C.; Yang, Q.; Jin, X.; Liu, N.; Wu, S.; Su, C. New Cn2 statistical model based on first radiosonde turbulence observation over Lhasa. J. Opt. Soc. Am. A 2020, 37, 995–1001. [Google Scholar] [CrossRef]
- Cai, J.; Li, X.B.; Zhan, G.W.; Wu, P.F.; Xu, C.Y.; Qing, C.; Wu, X.Q. A new model for the profiles of optical turbulence outer scale and Cn2 on the coast. Wuli Xuebao/Acta Phys. Sin. 2018, 67, 137–151. [Google Scholar] [CrossRef]
- Qing, C.; Wu, X.; Li, X.; Luo, T.; Su, C.; Zhu, W. Mesoscale optical turbulence simulations above Tibetan Plateau: First attempt. Opt. Express 2020, 28, 4571–4586. [Google Scholar] [CrossRef]
- Trinquet, H.; Vernin, J. A Model to Forecast Seeing and Estimate C2N Profiles from Meteorological Data. Publ. Astron. Soc. Pac. 2006, 118, 756–764. [Google Scholar] [CrossRef] [Green Version]
- Ruggiero, F.H.; Debenedictis, F.H. Forecasting optical turbulence from mesoscale numerical weather prediction models. In Proceedings of the DoD High Performance Modernization Program Users Group Conference, Austin, TX, USA, 10–14 June 2002. [Google Scholar]
- Roddier, F.; Gilli, J.M.; Lund, G. On the origin of speckle boiling and its effects in stellar speckle interferometry. J. Opt. 2000, 13, 263. [Google Scholar] [CrossRef]
- Han, Y.; Yang, Q.; Nana, L.; Zhang, K.; Qing, C.; Li, X.; Wu, X.; Luo, T. Analysis of wind-speed profiles and optical turbulence above Gaomeigu and the Tibetan Plateau using ERA5 data. Mon. Not. R. Astron. Soc. 2021, 501, 4692–4702. [Google Scholar] [CrossRef]
- Masciadri, E.; Vernin, J.; Bougeault, P.J.A. 3D numerical simulations of optical turbulence at the Roque de Los Muchachos Observatory using the atmospherical model Meso-Nh. Astron. Astrophys. 2001, 365, 699–708. [Google Scholar] [CrossRef] [Green Version]
- Takato, N.; Yamaguchi, I. Spatial correlation of Zernike phase-expansion coefficients for atmospheric turbulence with finite outer scale. J. Opt. Soc. Am. A 1995, 12, 958–963. [Google Scholar] [CrossRef]
- McHugh, J.; Jumper, G.; Chun, M. Balloon Thermosonde Measurements over Mauna Kea and Comparison with Seeing Measurements. Publ. Astron. Soc. Pac. 2008, 120, 1318–1324. [Google Scholar] [CrossRef]
- Tian, Q.; Jiang, P.; Jin, X.; Li, J.; Pei, C.; Du, F.; Li, Z.; Li, X.; Chen, H.; Ji, T.; et al. Discovery of high-quality daytime seeing windows at the Antarctic Taishan station. Mon. Not. R. Astron. Soc. 2020, 493, 5648–5652. [Google Scholar] [CrossRef]






| Parameters | Wavelength (nm) | Detection Distance (m) | Wind Speed Detection Range (m/s) | Wind Direction Detection Range (°) | Vertical Resolution (m) |
|---|---|---|---|---|---|
| Value | 1550 | 30–10,000 | 0–75 | 0–360 | 30/50/100/200 |
| Parameters | Detection Distance (m) | Temperature Detection Range (°C) | Temporal Resolution (s) | Vertical Resolution (m) |
|---|---|---|---|---|
| Value | 0–10,000 | −60–40 | 1 | 50 |
| Instruments | Measurement Parameters | Working Status |
|---|---|---|
| PCDL | Wind speed, wind direction | Continuous |
| Microwave radiometer | Temperature, humidity | Continuous |
| Micro-thermometer | Turbulence strength (3 m above ground level) | Continuous |
| Radiosonde | Turbulence strength (0–30 km) | Intermittent |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Zhou, L.; Shao, S.; Weng, N.; Liu, Q. Analyzing the Effects of a Basin on Atmospheric Environment Relevant to Optical Turbulence. Photonics 2022, 9, 235. https://doi.org/10.3390/photonics9040235
Xu M, Zhou L, Shao S, Weng N, Liu Q. Analyzing the Effects of a Basin on Atmospheric Environment Relevant to Optical Turbulence. Photonics. 2022; 9(4):235. https://doi.org/10.3390/photonics9040235
Chicago/Turabian StyleXu, Manman, Liangping Zhou, Shiyong Shao, Ningquan Weng, and Qing Liu. 2022. "Analyzing the Effects of a Basin on Atmospheric Environment Relevant to Optical Turbulence" Photonics 9, no. 4: 235. https://doi.org/10.3390/photonics9040235
APA StyleXu, M., Zhou, L., Shao, S., Weng, N., & Liu, Q. (2022). Analyzing the Effects of a Basin on Atmospheric Environment Relevant to Optical Turbulence. Photonics, 9(4), 235. https://doi.org/10.3390/photonics9040235





