Processing-Speed Enhancement in a Delay-Laser-Based Reservoir Computer by Optical Injection
Abstract
:1. Introduction
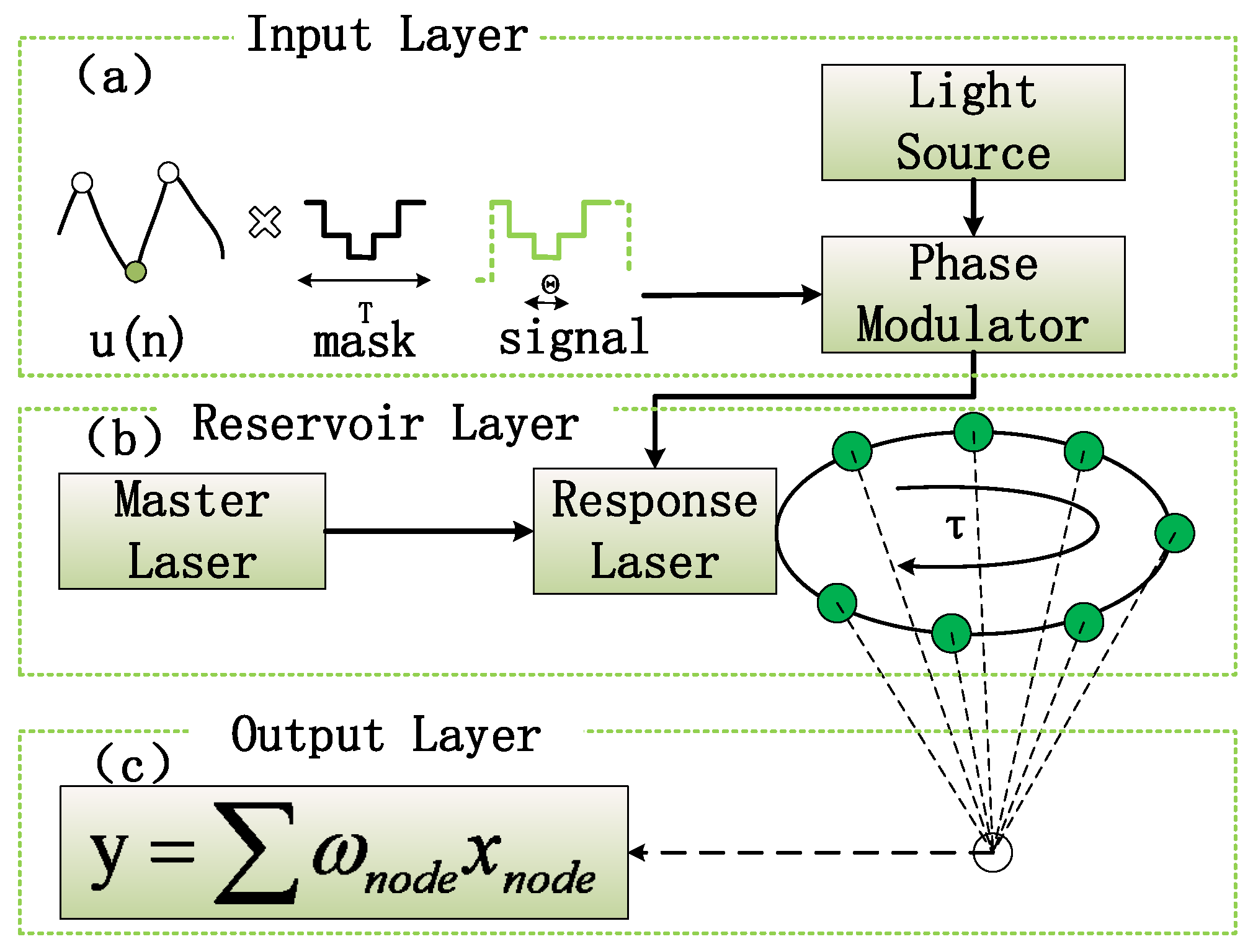
2. Methods
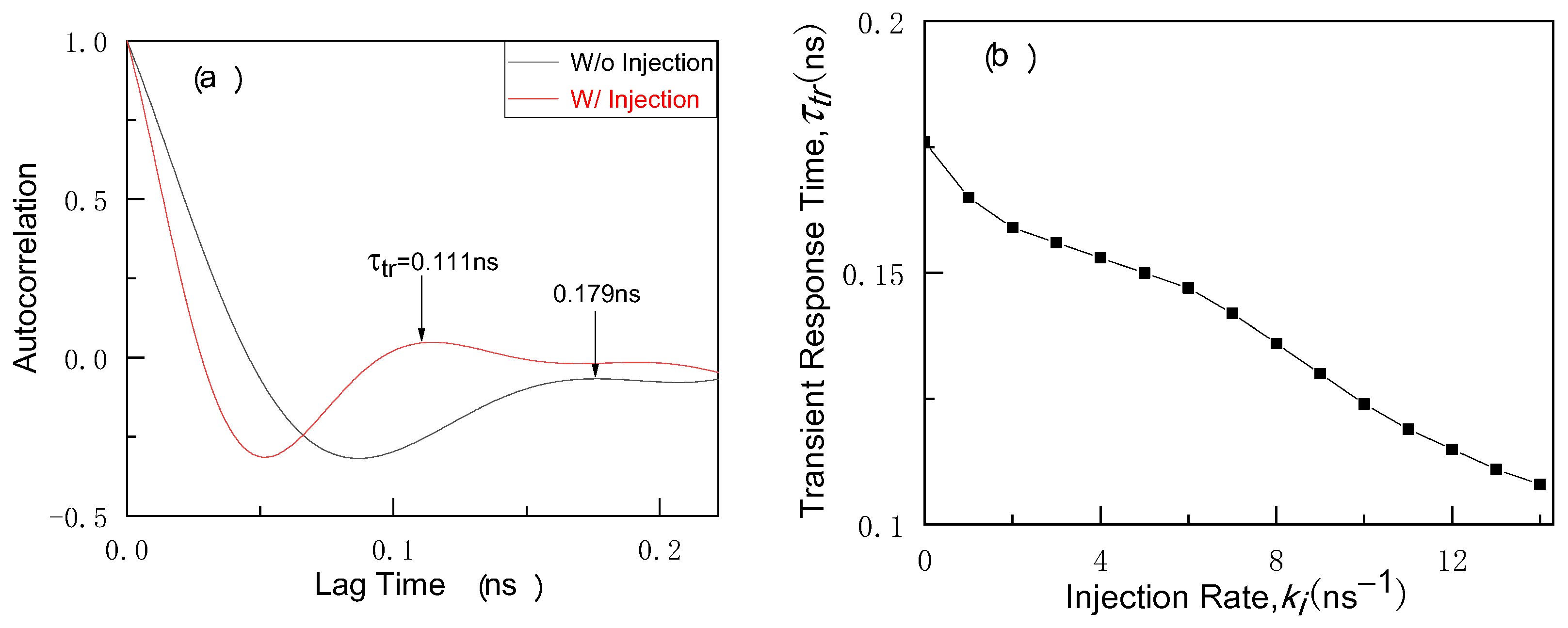
3. Transient Dynamics of Response Laser
4. Results
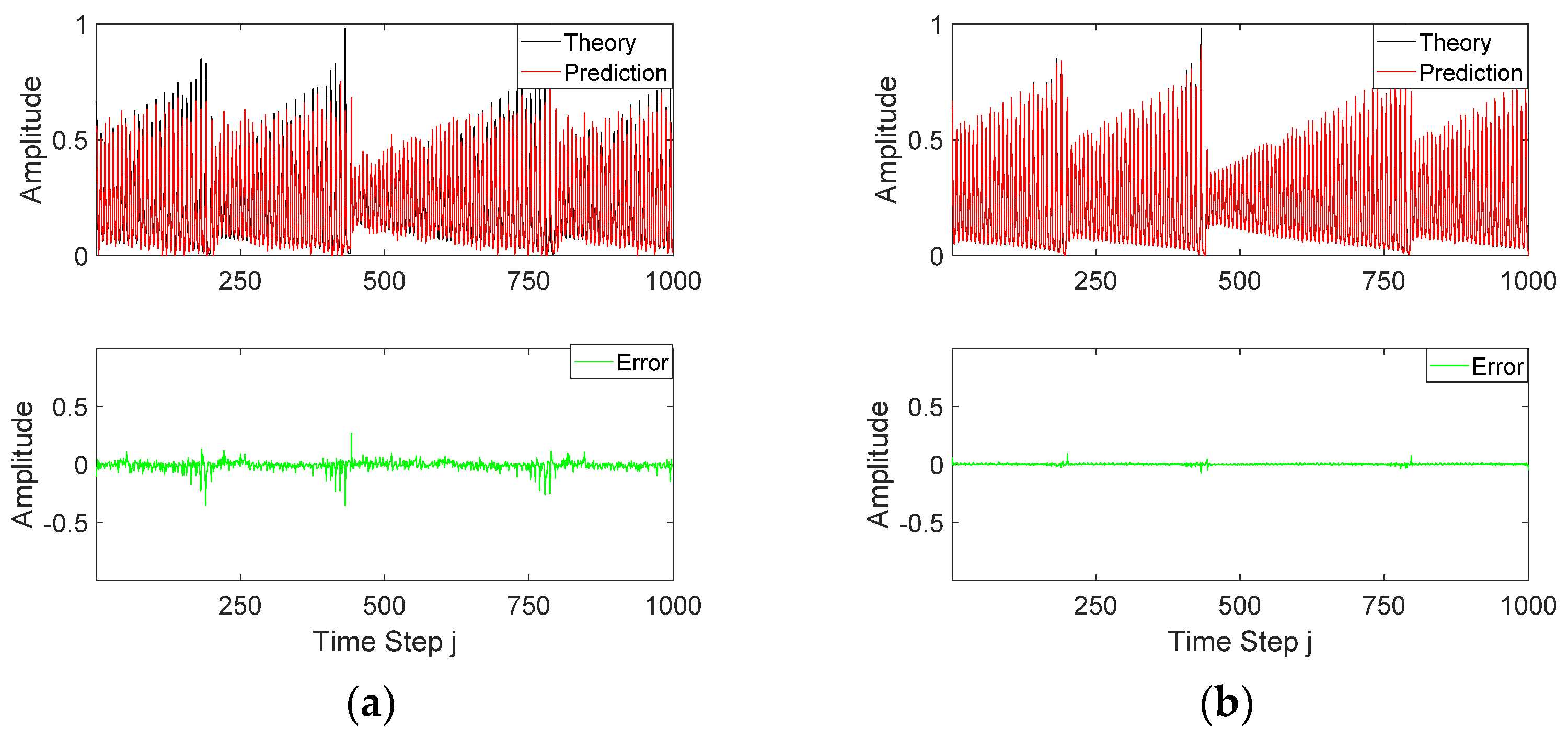
4.1. Chaotic Time-Series Prediction
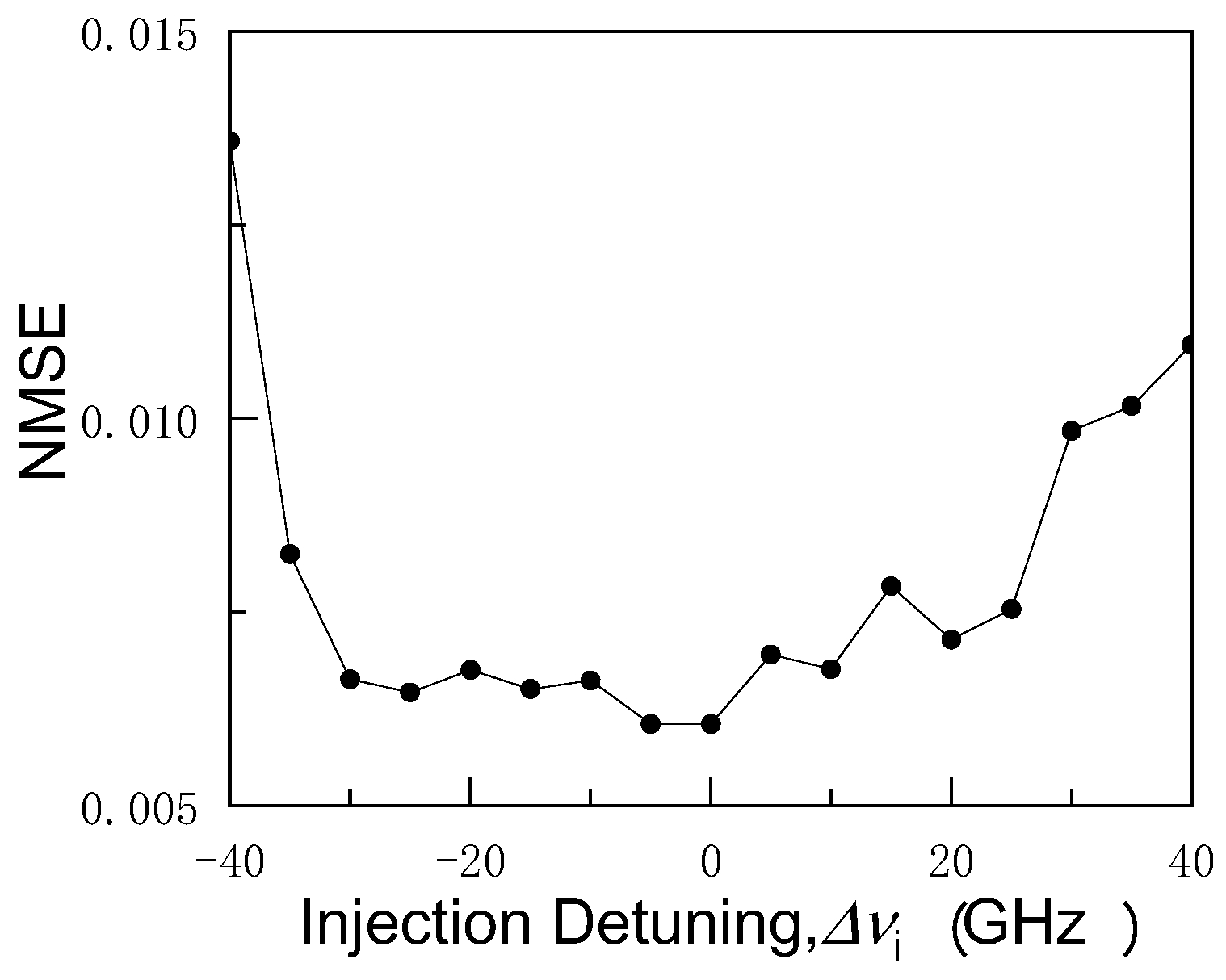
4.1.1. Dependencies on Injection Parameters
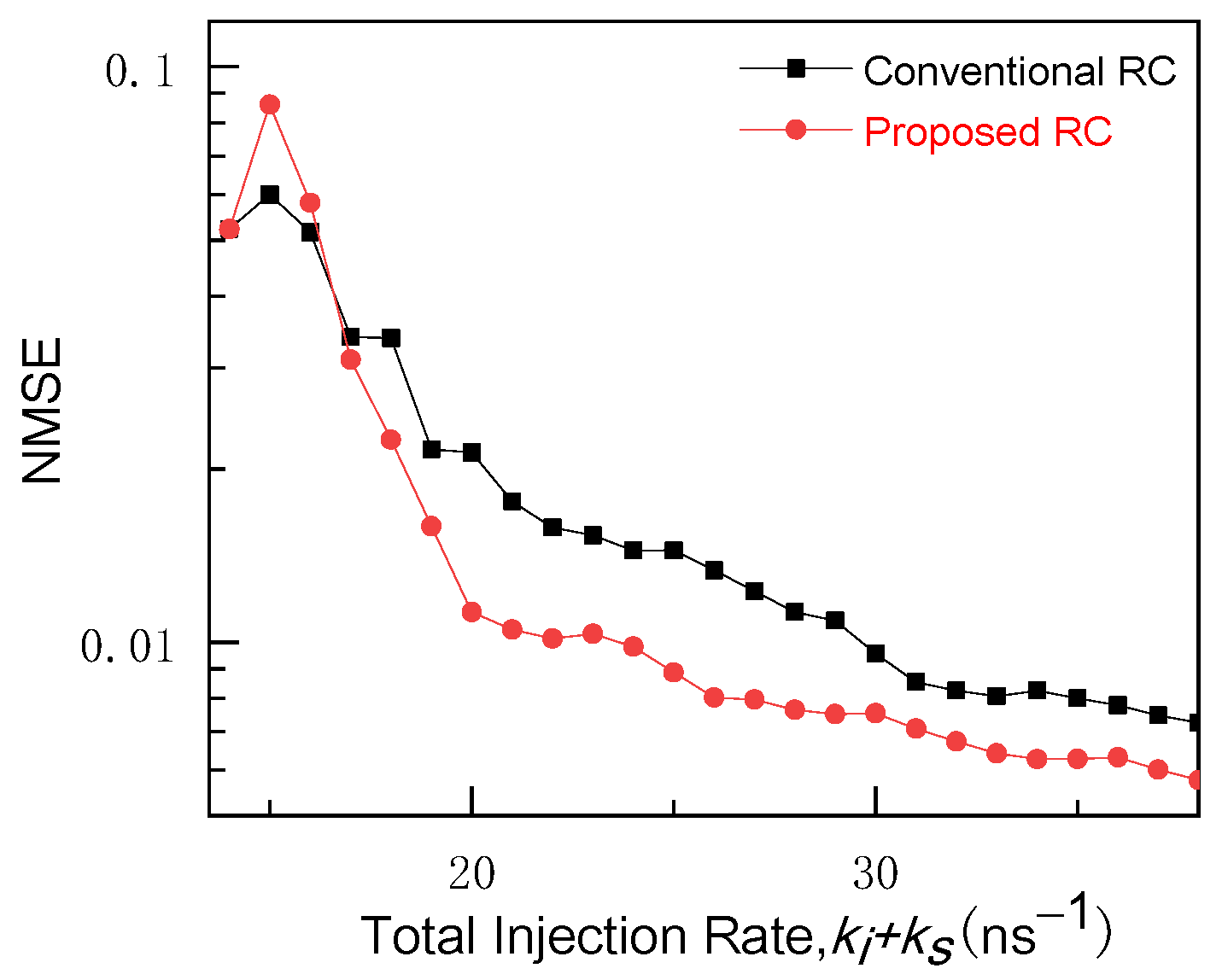
4.1.2. Processing-Speed Enhancement
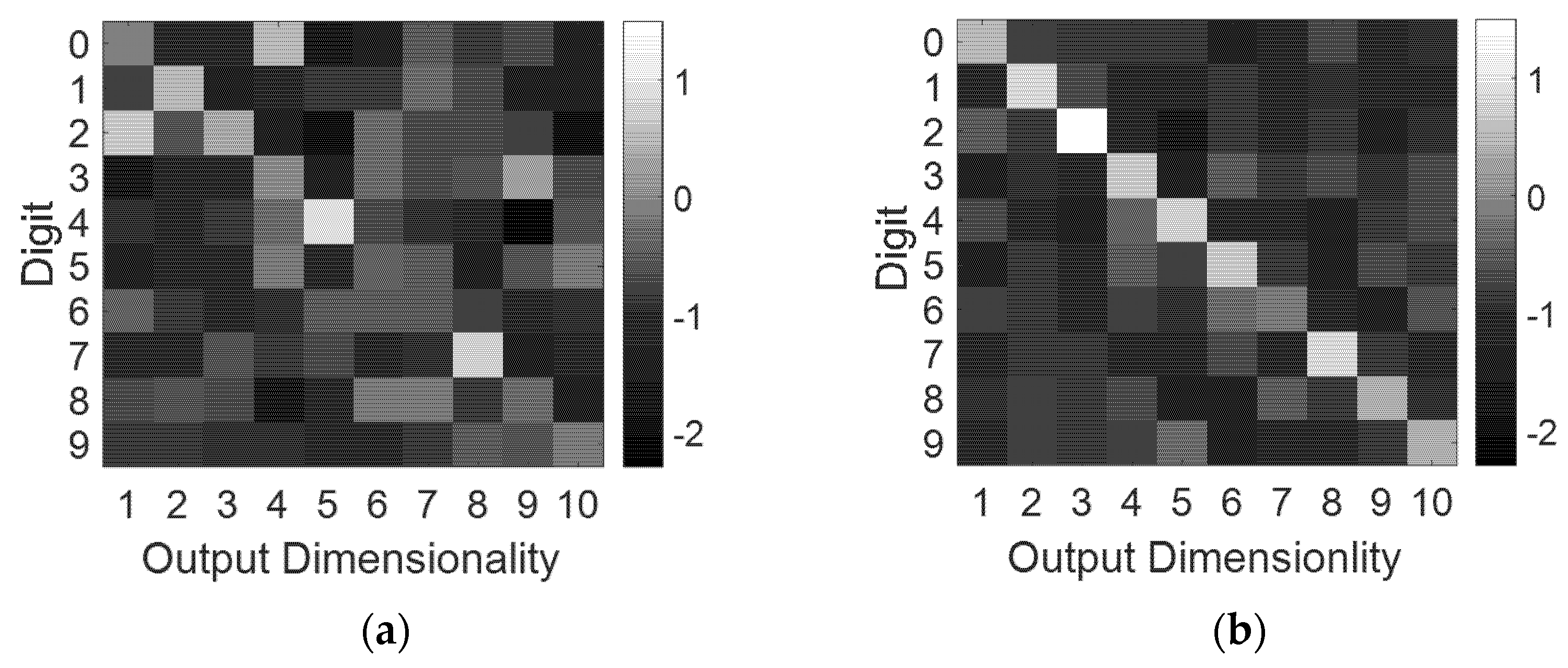
4.2. Handwritten Digit Recognition
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scardapane, S.; Gallicchio, C.; Micheli, A. Guest Editorial: Trends in Reservoir Computing. Cogn. Comput. 2021, 1–2. [Google Scholar] [CrossRef]
- Van der Sande, G.; Brunner, D.; Soriano, M.C. Advances in photonic reservoir computing. Nanophotonics 2017, 6, 561–576. [Google Scholar] [CrossRef]
- Woods, D.; Naughton, T. Photonic neural networks. Nat. Phys. 2012, 8, 257–259. [Google Scholar] [CrossRef]
- Lukoševičius, M.; Jaeger, S.; Schrauwen, H.B. Reservoir Computing Trends. Künstl. Intell. 2012, 26, 365–371. [Google Scholar] [CrossRef]
- Sunada, S.; Uchida, A. Photonic reservoir computing based on nonlinear wave dynamics at microscale. Sci. Rep. 2019, 9, 19078. [Google Scholar] [CrossRef] [Green Version]
- Appeltant, L.; Soriano, M.C.; Van der Sande, G.; Danckaert, J.; Massar, S.; Dambre, J.; Schrauwen, B.; Mirasso, C.R.; Fischer, I. Information processing using a single dynamical node as complex system. Nat. Commun. 2011, 2, 468. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brunner, D.; Soriano, M.C.; Mirasso, C.R.; Fischer, I. Parallel photonic information processing at gigabyte per second data rates using transient states. Nat. Commun. 2013, 4, 1364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hou, Y.S.; Xia, G.Q.; Jayaprasath, E. Parallel information processing using a reservoir computing system based on mutually coupled semiconductor lasers. Appl. Phys. 2020, 40, 126. [Google Scholar] [CrossRef]
- Nguimdo, R.M.; Verschaffelt, G.; Danckaert, J.; Van der Sande, G. Simultaneous Computation of Two Independent Tasks Using Reservoir Computing Based on a Single Photonic Nonlinear Node with Optical Feedback. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3301–3307. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.X.; Xiang, S.Y.; Zhang, Y.H. Enhanced memory capacity of a neuromorphic reservoir computing system based on a VCSEL with double optical feedbacks. Sci. China Inf. Sci. 2020, 63, 160407. [Google Scholar] [CrossRef]
- Harkhoe1, K.; Van der Sande, G. Delay-Based Reservoir Computing Using Multimode Semiconductor Lasers: Exploiting the Rich Carrier Dynamics. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1502909. [Google Scholar] [CrossRef]
- Guo, X.X.; Xiang, S.Y.; Zhang, Y.H.; Lin, L.; Wen, A.J.; Hao, Y. Polarization Multiplexing Reservoir Computing Based on a VCSEL with Polarized Optical Feedback. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1700109. [Google Scholar] [CrossRef]
- Bueno, J.; Brunner, D.; Soriano, M.C.; Fischer, I. Conditions for reservoir computing performance using semiconductor lasers with delayed optical feedback. Opt. Express 2017, 25, 2401–2412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, X.X.; Xiang, S.Y.; Zhang, Y.H.; Lin, L.; Wen, A.J.; Hao, Y. High-Speed Neuromorphic Reservoir Computing Based on a Semiconductor Nanolaser with Optical Feedback Under Electrical Modulation. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1500707. [Google Scholar] [CrossRef]
- Larger, L.; Baylón-Fuentes, A.; Martinenghi, R.; Udaltsov, V.S.; Chembo, Y.K.; Jacquot, M. High-speed photonic reservoir computing using a time-delay-based architecture: Million words per second classification. Phys. Rev. X 2017, 7, 011015. [Google Scholar] [CrossRef]
- Yue, D.Z.; Wu, Z.M.; Hou, Y.S.; Hu, C.X.; Jiang, Z.F.; Xia, G.Q. Reservoir Computing Based on Two Parallel Reservoirs under Identical Electrical Message Injection. IEEE Photon. J. 2021, 13, 7800311. [Google Scholar] [CrossRef]
- Martinenghi, R.; Rybalko, S.; Jacquot, M.; Chembo, Y.; Larger, L. Photonic nonlinear transient computing with multiple-delay wavelength d ynamics. Phys. Rev. Lett. 2012, 108, 244101. [Google Scholar] [CrossRef] [Green Version]
- Nguimdo, R.; Verschaffelt, G.; Danckaert, J.; Van der Sande, G. Fast photonic information processing using semiconductor lasers with delayed optical feedback: Role of phase dynamics. Opt. Express 2014, 7, 72–86. [Google Scholar] [CrossRef]
- Nakayama, J.; Kanno, K.; Uchida, A. Laser dynamical reservoir computing with consistency: An approach of a chaos mask signal. Opt. Express 2016, 24, 79–92. [Google Scholar] [CrossRef]
- Kuriki, Y.; Nakayama, J.; Takano, K.; Uchida, A. Impact of input mask signals on delay-based photonic reservoir computing with semiconductor lasers. Opt. Express 2018, 26, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Duport, F.; Schneider, B.; Smerieri, A.; Haelterman, M.; Massar, S. All-optical reservoir computing. Opt. Express 2012, 20, 783–795. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhou, P.; Yang, Y.; Li, N.Q. High-speed photonic reservoir computer based on a delayed Fano laser under electrical modulation. Opt. Lett. 2021, 46, 35–38. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.X.; Xiang, S.Y.; Zhang, Y.H.; Lin, L.; Wen, A.J.; Hao, Y. Four-channels reservoir computing based on polarization dynamics in mutually coupled VCSELs system. Opt. Express 2019, 27, 23293–23306. [Google Scholar] [CrossRef] [PubMed]
- Vatin, J.; Rontani, D.; Sciamanna, M. Enhanced performance of a reservoir computer using polarization dynamics in VCSELs. Opt. Lett. 2018, 43, 4497–4500. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Uchida, A. Optical Communication with Chaotic Lasers, Applications of Nonlinear Dynamics and Synchronization; Wiley-VCH: Hoboken, NJ, USA, 2012; pp. 156–192. [Google Scholar]
- Chan, S.C.; Hwang, S.K.; Liu, J.M. Period-one oscillation for photonic microwave transmission using an optically injected semiconductor laser. Opt. Express 2007, 15, 14921–14935. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Chan, S. Chaotic Time-Delay Signature Suppression in a Semiconductor Laser with Frequency-Detuned Grating Feedback. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 541–552. [Google Scholar]
- Simpson, T.B.; Liu, J.M.; Gavrielides, A. Bandwidth enhancement and broadband noise reduction in injection-locked semiconductor laser. IEEE Photon. Technol. Lett. 1995, 7, 709–711. [Google Scholar] [CrossRef]
- Wang, J.; Haldar, M.K.; Li, L.; Mendis, F.V.C. Enhancement of modulation bandwidth of laser diodes by injection locking. IEEE Photon. Technol. Lett. 1996, 8, 34–36. [Google Scholar] [CrossRef]
- Harkhoe, K.; Van der Sande, G. Task-Independent Computational Abilities of Semiconductor Lasers with Delayed Optical Feedback for Reservoir Computing. Photonics 2019, 6, 124. [Google Scholar] [CrossRef] [Green Version]
- Hübner, U.; Abraham, N.; Weiss, C. Dimensions and entropies of chaotic intensity pulsations in a single-mode far-infrared NH3 laser. Phys. Rev. A 1989, 11, 54–65. [Google Scholar]
- Weigend, A.S.; Gershenfeld, N.A. Time Series Prediction: Forecasting the Future and Understanding the Past; 1993. Available online: http://wwwpsych.stanford.edu/~andreas/Time-Series/SantaFe.html (accessed on 31 March 2022).
- Paquot, Y.; Duport, F.; Smerieri, A. Optoelectronic Reservoir Computing. Sci. Rep. 2012, 2, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Ortín, S.; Pesquera, L. Delay-based reservoir computing: Tackling performance degradation due to system response time. Opt. Lett. 2020, 45, 905–908. [Google Scholar] [CrossRef] [PubMed]
- Yue, D.Z.; Xia, G.Q.; Iayaprasath, E.; Yue, D.Z.; Yang, W.Y.; Wu, Z.M. Prediction and classification performance of reservoir computing system using mutually delay-coupled semiconductor lasers. Opt. Commun. 2019, 433, 215–220. [Google Scholar]
- Nguimdo, R.M.; Antonik, P.; Marsal, N.; Rontani, D. Impact of optical coherence on the performance of large-scale spatiotemporal photonic reservoir computing systems. Opt. Express 2020, 28, 27989–28005. [Google Scholar] [CrossRef]

| Parameters | Designation | Value |
|---|---|---|
| Linewidth enhancement factor | ||
| Gain coefficient | ||
| Carrier density at transparency | ||
| Gain saturation | ||
| Injection current of the response laser | J | |
| Carrier lifetime | ||
| Photon lifetime | ||
| Intensity of light source/master laser | ||
| Coupling strength of light source | ||
| Coupling detuning frequency of light source | ||
| Injection rate of master laser | ||
| Detuning frequency of master laser | ||
| Node number of delay loop | 100 | |
| Interval of node | ||
| Holding time in input layer | ||
| Loop delay time |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, S.-S.; Zou, X.; Pan, W.; Yan, L. Processing-Speed Enhancement in a Delay-Laser-Based Reservoir Computer by Optical Injection. Photonics 2022, 9, 240. https://doi.org/10.3390/photonics9040240
Li Z, Li S-S, Zou X, Pan W, Yan L. Processing-Speed Enhancement in a Delay-Laser-Based Reservoir Computer by Optical Injection. Photonics. 2022; 9(4):240. https://doi.org/10.3390/photonics9040240
Chicago/Turabian StyleLi, Ziyue, Song-Sui Li, Xihua Zou, Wei Pan, and Lianshan Yan. 2022. "Processing-Speed Enhancement in a Delay-Laser-Based Reservoir Computer by Optical Injection" Photonics 9, no. 4: 240. https://doi.org/10.3390/photonics9040240
APA StyleLi, Z., Li, S.-S., Zou, X., Pan, W., & Yan, L. (2022). Processing-Speed Enhancement in a Delay-Laser-Based Reservoir Computer by Optical Injection. Photonics, 9(4), 240. https://doi.org/10.3390/photonics9040240





