Multiparameter Sensing Based on Tunable Fano Resonances in MIM Waveguide Structure with Square-Ring and Triangular Cavities
Abstract
:1. Introduction
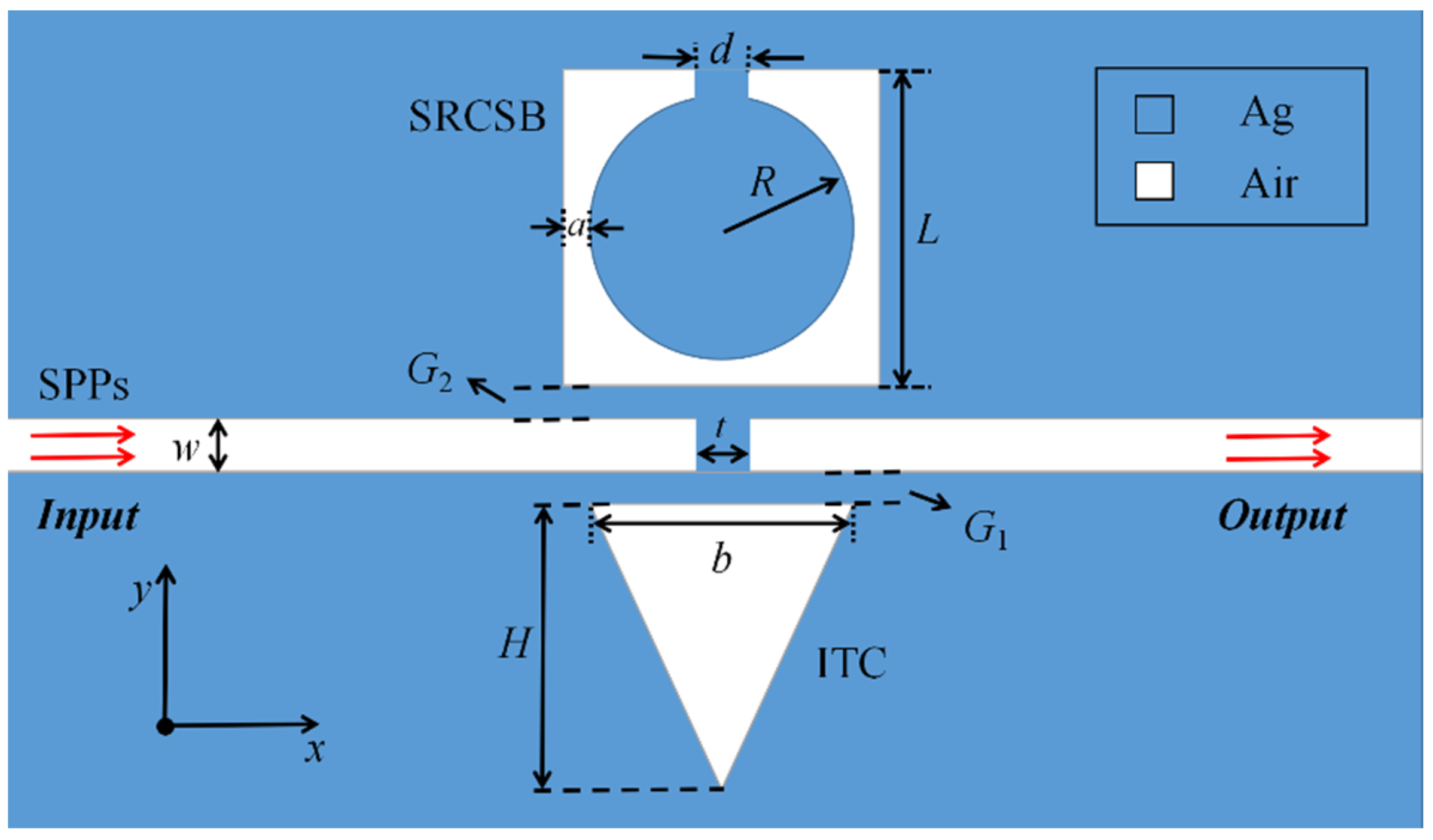
2. Materials and Methods
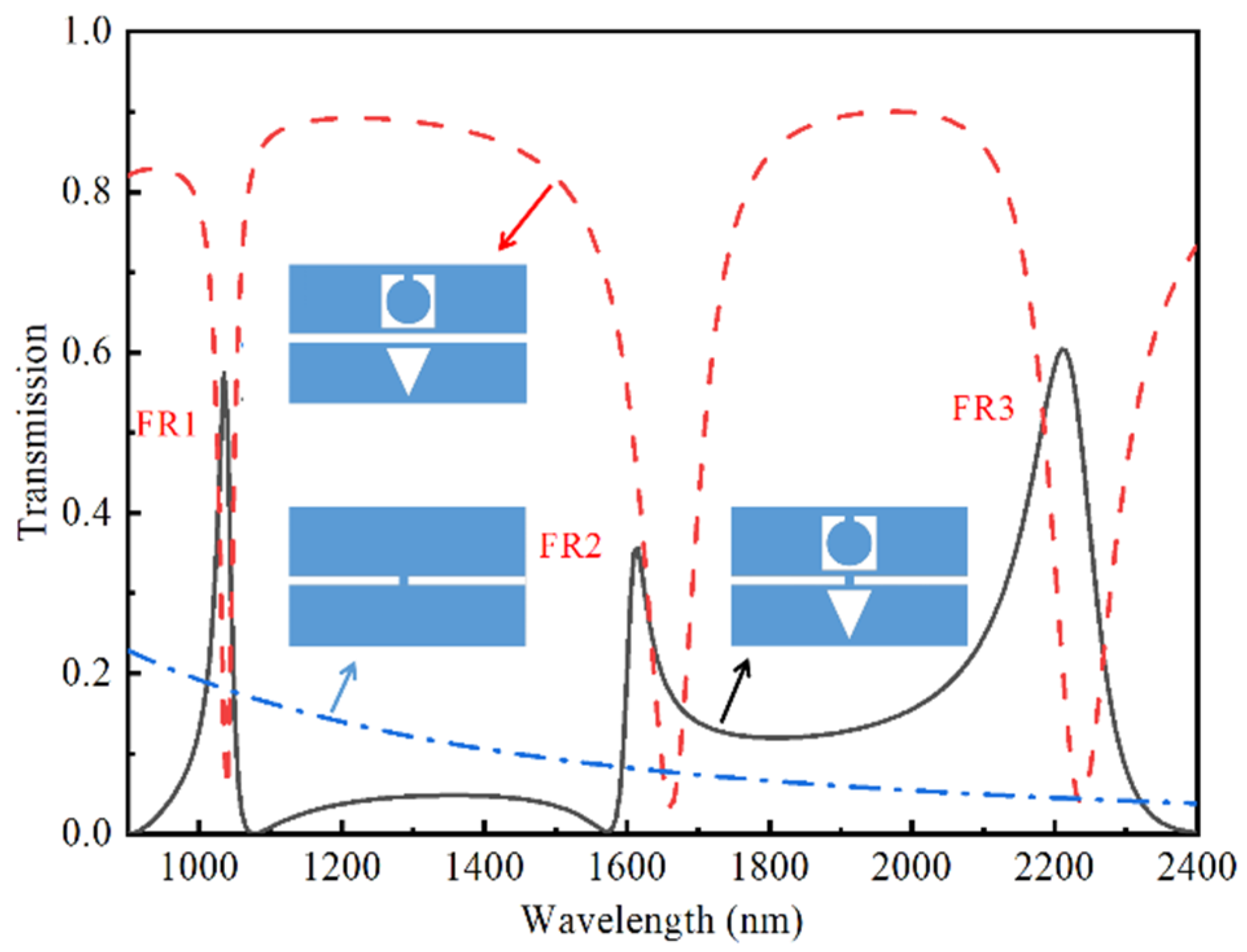
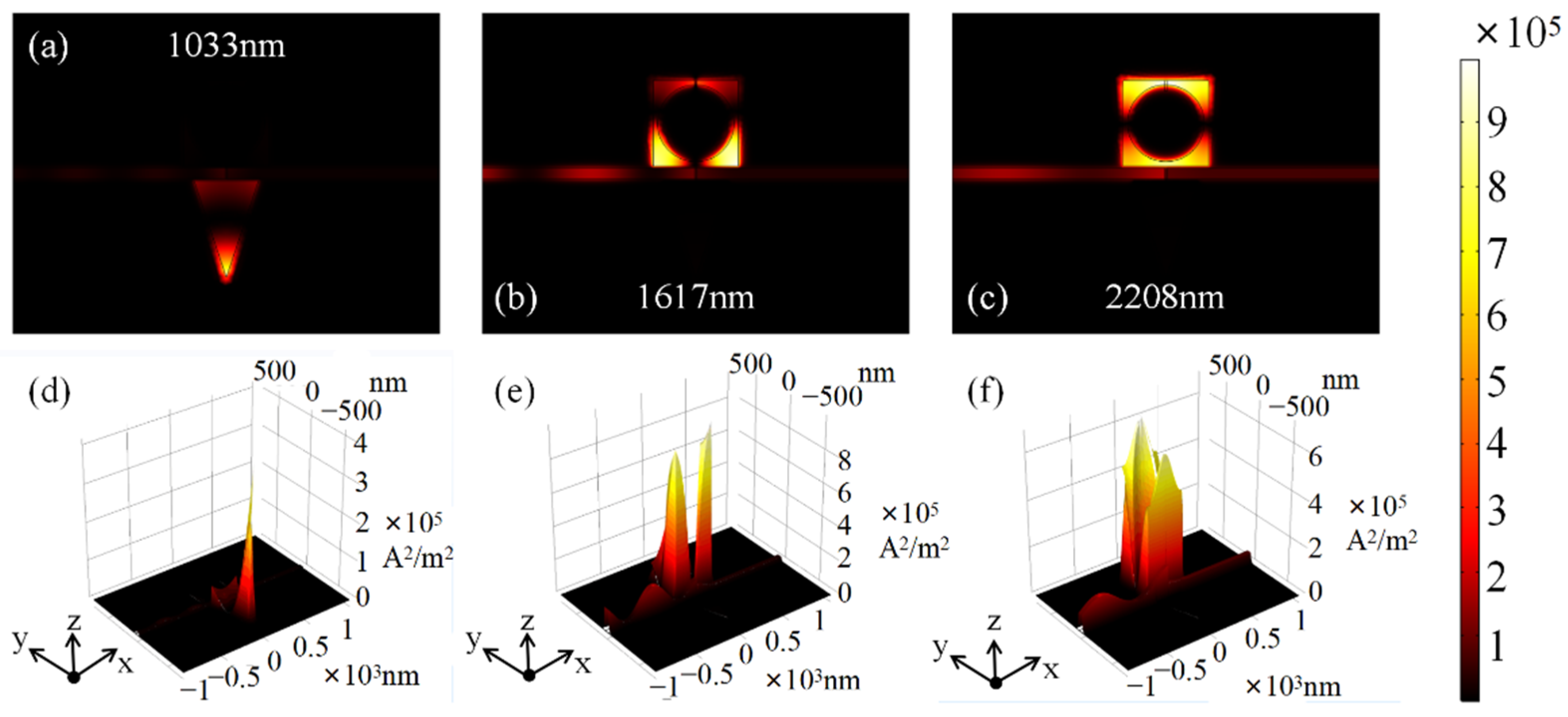
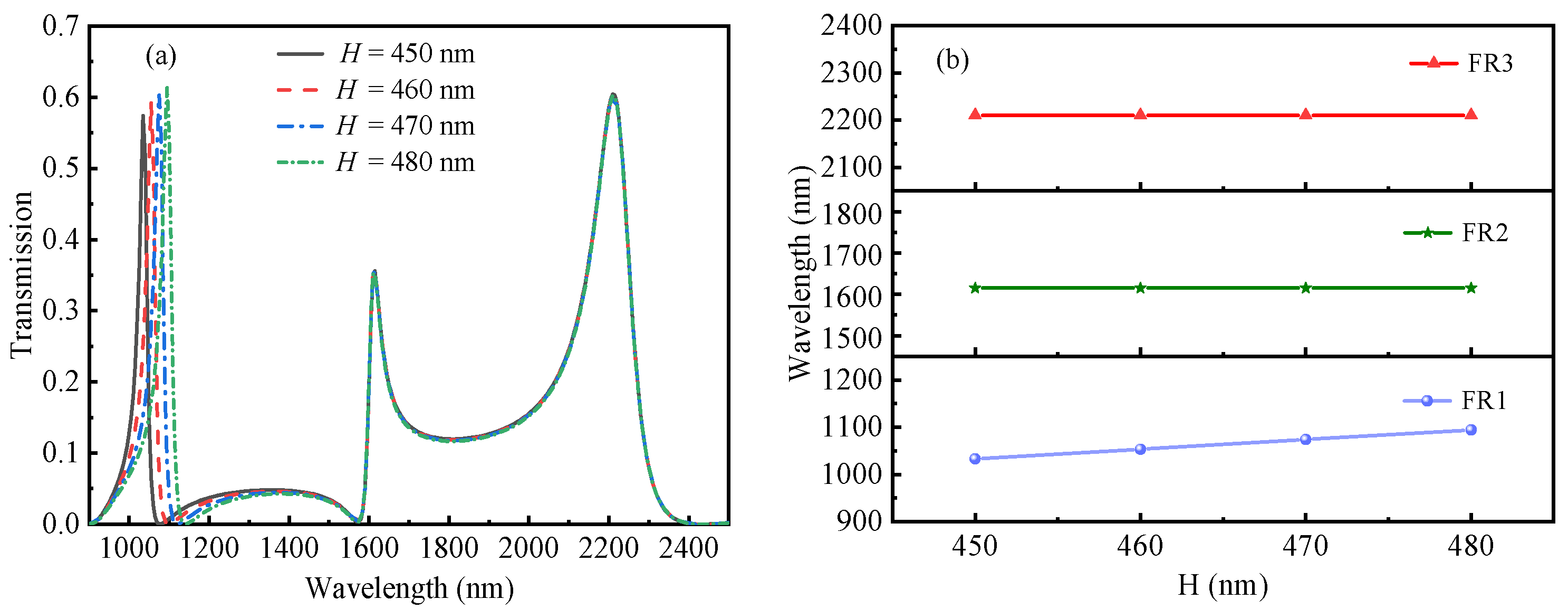
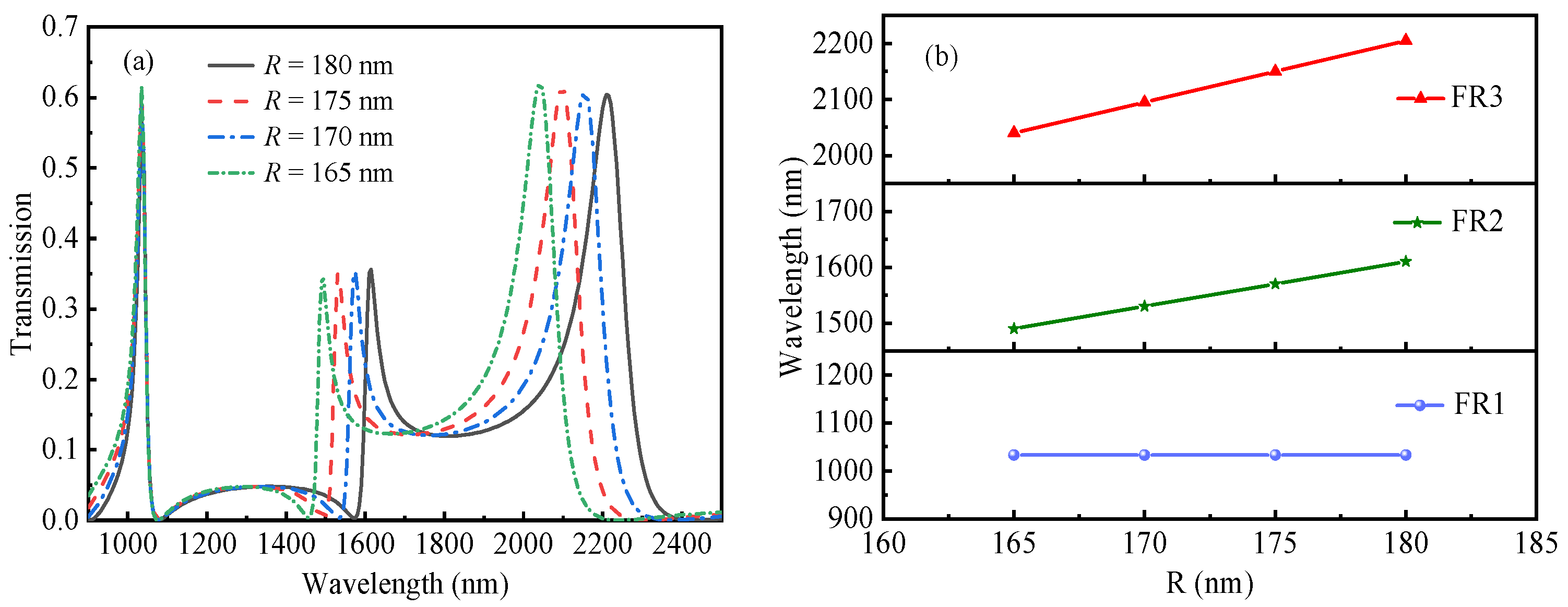
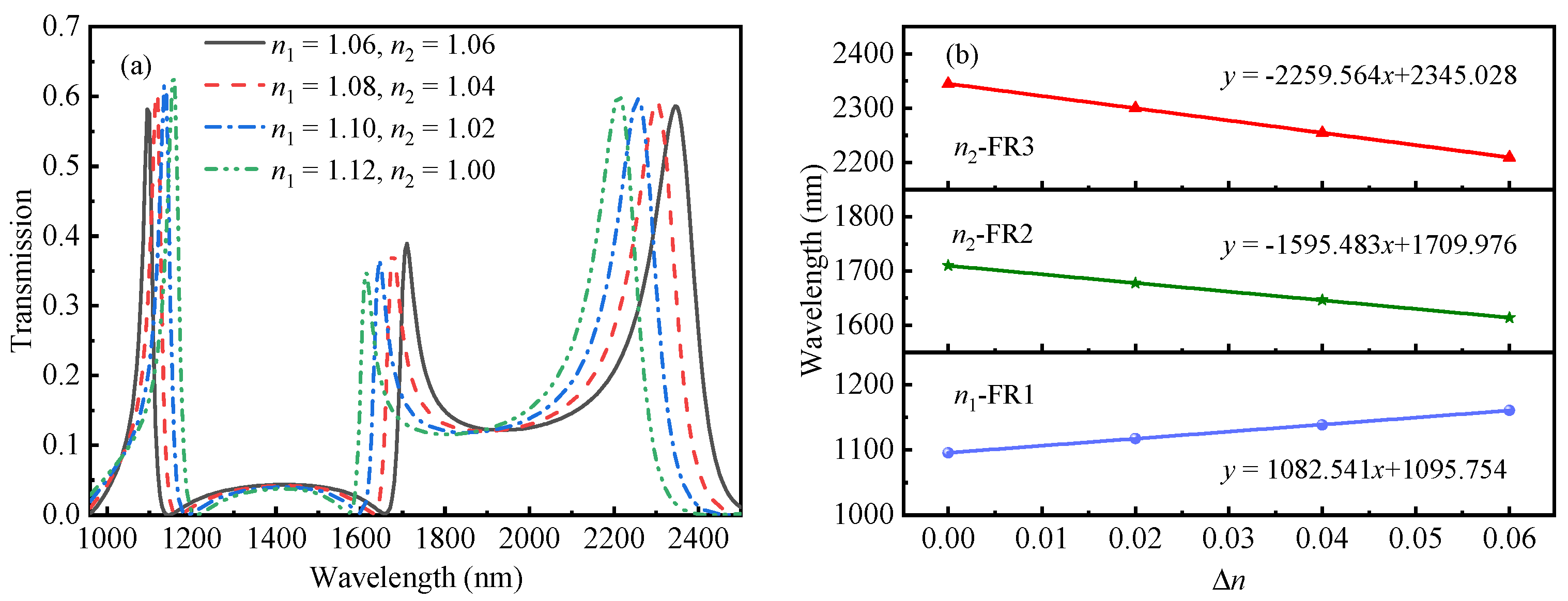
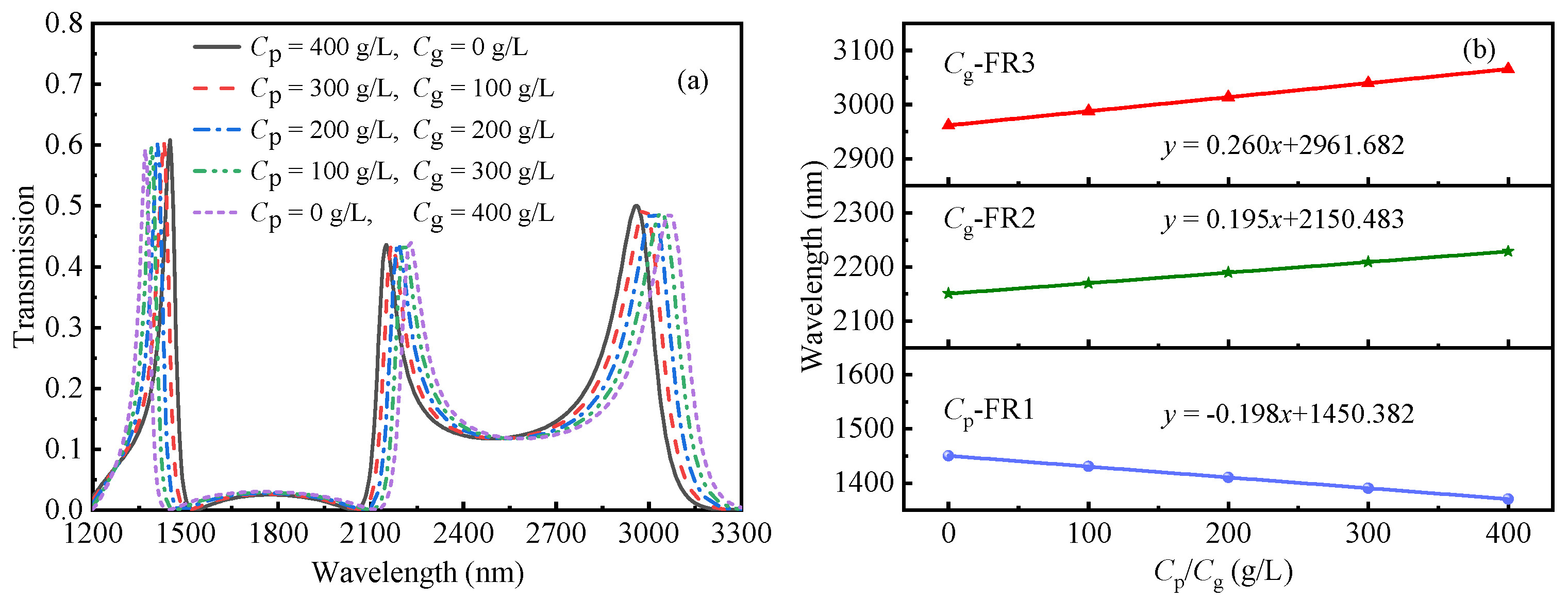
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Bao, K.; Halas, N.J.; Xu, H.; Nordlander, P. Substrate-Induced Fano Resonances of a Plasmonic: Nanocube: A Route to Increased-Sensitivity Localized Surface Plasmon Resonance Sensors Revealed. Nano Lett. 2011, 11, 1657–1663. [Google Scholar] [CrossRef]
- Verellen, N.; Sonnefraud, Y.; Sobhani, H.; Hao, F.; Moshchalkov, V.V.; Van Dorpe, P.; Nordlander, P.; Maier, S.A. Fano Resonances in Individual Coherent Plasmonic Nanocavities. Nano Lett. 2009, 9, 1663–1667. [Google Scholar] [CrossRef] [PubMed]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef] [Green Version]
- Luk’yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef] [PubMed]
- Limonov, M.F.; Rybin, M.V.; Poddubny, A.N.; Kivshar, Y.S. Fano resonances in photonics. Nat. Photonics 2017, 11, 543–554. [Google Scholar] [CrossRef]
- Lassiter, J.B.; Sobhani, H.; Fan, J.A.; Kundu, J.; Capasso, F.; Nordlander, P.; Halas, N.J. Fano Resonances in Plasmonic Nanoclusters: Geometrical and Chemical Tunability. Nano Lett. 2010, 10, 3184–3189. [Google Scholar] [CrossRef]
- Fan, S.H.; Suh, W.; Joannopoulos, J.D. Temporal coupled-mode theory for the Fano resonance in optical resonators. J. Opt. Soc. Am. A 2003, 20, 569–572. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.; Al-Naib, I.A.I.; Koch, M.; Zhang, W. Sharp Fano resonances in THz metamaterials. Opt. Express 2011, 19, 6312–6319. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.; Liu, X.; Mao, D.; Wang, G. Plasmonic nanosensor based on Fano resonance in waveguide-coupled resonators. Opt. Lett. 2012, 37, 3780–3782. [Google Scholar] [CrossRef]
- Liu, G.; Cheng, D.; Zhang, B.; Shu, G.X.; Wang, J.X. A microwave biosensor based on spoof surface plasmon polaritons for in vivo measurement of the water content of human skin tissues. J. Phys. D Appl. Phys. 2019, 52, 205401. [Google Scholar] [CrossRef]
- Sun, M.T.; Hou, Y.X.; Xu, H.X. Can information of chemical reaction propagate with plasmonic waveguide and be detected at remote terminal of nanowire? Nanoscale 2011, 3, 4114–4116. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Z.; Yan, S. Tunable Fano Resonance in Asymmetric MIM Waveguide Structure. Sensors 2017, 17, 1494. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Kuang, Y.; Zhang, Z.; Tang, Y.; Han, J.; Wang, R.; Cui, J.; Hou, Y.; Liu, W. High-sensitivity refractive index sensors based on Fano resonance in the plasmonic system of splitting ring cavity-coupled MIM waveguide with tooth cavity. Appl. Phys. A 2019, 125, 13. [Google Scholar] [CrossRef]
- Refki, S.; Hayashi, S.; Ishitobi, H.; Nesterenko, D.V.; Rahmouni, A.; Inouye, Y.; Sekkat, Z. Resolution Enhancement of Plasmonic Sensors by Metal-Insulator-Metal Structures. Ann. Phys. 2018, 530, 1700411. [Google Scholar] [CrossRef]
- Sekkat, Z.; Hayashi, S.; Nesterenko, D.V.; Rahmouni, A.; Refki, S.; Ishitobi, H.; Inouye, Y.; Kawata, S. Plasmonic coupled modes in metal-dielectric multilayer structures: Fano resonance and giant field enhancement. Opt. Express 2016, 24, 20080–20088. [Google Scholar] [CrossRef]
- Andam, N.; Refki, S.; Hayashi, S.; Sekkat, Z. Plasmonic mode coupling and thin film sensing in metal-insulator-metal structures. Sci. Rep. 2021, 11, 15093. [Google Scholar] [CrossRef]
- Nasari, H.; Abrishamian, M.S.; Berini, P. Nonlinear optics of surface plasmon polaritons in subwavelength graphene ribbon resonators. Opt. Express 2016, 24, 708–723. [Google Scholar] [CrossRef]
- Zafar, R.; Salim, M. Wideband slow light achievement in MIM plasmonic waveguide by controlling Fano resonance. Infrared Phys. Technol. 2014, 67, 25–29. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, M.; Wang, Y.; Zhao, R.; Yan, S. Fano Resonance in an Asymmetric MIM Waveguide Structure and Its Application in a Refractive Index Nanosensor. Sensors 2019, 19, 791. [Google Scholar] [CrossRef] [Green Version]
- Qi, J.; Chen, Z.; Chen, J.; Li, Y.; Qiang, W.; Xu, J.; Sun, Q. Independently tunable double Fano resonances in asymmetric MIM waveguide structure. Opt. Express 2014, 22, 14688–14695. [Google Scholar] [CrossRef]
- Pang, S.; Huo, Y.; Xie, Y.; Hao, L. Fano resonance in MIM waveguide structure with oblique rectangular cavity and its application in sensor. Opt. Commun. 2016, 381, 409–413. [Google Scholar] [CrossRef]
- Li, Z.; Wen, K.; Chen, L.; Lei, L.; Zhou, J.; Zhou, D.; Fang, Y.; Wu, B. Control of Multiple Fano Resonances Based on a Subwavelength MIM Coupled Cavities System. IEEE Access 2019, 7, 59369–59375. [Google Scholar] [CrossRef]
- Chen, Z.; Song, X.; Duan, G.; Wang, L.; Yu, L. Multiple Fano Resonances Control in MIM Side-Coupled Cavities Systems. IEEE Photonics J. 2015, 7, 2433012. [Google Scholar] [CrossRef]
- Li, Z.; Wen, K.; Chen, L.; Lei, L.; Zhou, J.; Zhou, D.; Fang, Y.; Wu, B. Refractive index sensor based on multiple Fano resonances in a plasmonic MIM structure. Appl. Opt. 2019, 58, 4878–4883. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Poon, A.W. Fano resonance-based electrically reconfigurable add-drop filters in silicon microring resonator-coupled Mach-Zehnder interferometers. Opt. Lett. 2007, 32, 781–783. [Google Scholar] [CrossRef] [PubMed]
- Song, J.F.; Ochiai, Y.; Bird, J.P. Fano resonances in open quantum dots and their application as spin filters. Appl. Phys. Lett. 2003, 82, 4561–4563. [Google Scholar] [CrossRef]
- Qiang, Z.; Yang, H.; Chen, L.; Pang, H.; Ma, Z.; Zhou, W. Fano filters based on transferred silicon nanomembranes on plastic substrates. Appl. Phys. Lett. 2008, 93, 061106. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Khanikaev, A.B.; Shvets, G. Broadband Slow Light Metamaterial Based on a Double-Continuum Fano Resonance. Phys. Rev. Lett. 2011, 106, 107403. [Google Scholar] [CrossRef]
- Jiang, C.; Jiang, L.; Yu, H.; Cui, Y.; Li, X.; Chen, G. Fano resonance and slow light in hybrid optomechanics mediated by a two-level system. Phys. Rev. A 2017, 96, 053821. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, L.; Xue, C.; Zhang, W.; Yan, S. Fano Resonance Based on Metal-Insulator-Metal Waveguide-Coupled Double Rectangular Cavities for Plasmonic Nanosensors. Sensors 2016, 16, 642. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Tejeira, F.; Paniagua-Dominguez, R.; Sanchez-Gil, J.A. High-Performance Nanosensors Based on Plasmonic Fano-like Interference: Probing Refractive Index with Individual Nanorice and Nanobelts. ACS Nano 2012, 6, 8989–8996. [Google Scholar] [CrossRef]
- Chen, Z.-Q.; Qi, J.-W.; Chen, J.; Li, Y.-D.; Hao, Z.-Q.; Lu, W.-Q.; Xu, J.-J.; Sun, Q. Fano Resonance Based on Multimode Interference in Symmetric Plasmonic Structures and its Applications in Plasmonic Nanosensors. Chin. Phys. Lett. 2013, 30, 057301. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Chen, J.; Rohimah, S.; Tian, H.; Wang, J. Independently tunable triple Fano resonances based on MIM waveguide structure with a semi-ring cavity and its sensing characteristics. Opt. Express 2021, 29, 20829–20838. [Google Scholar] [CrossRef]
- Ji, P.; Shi, Q.; Zheng, L.; Wang, G.; Chen, F. High sensitivity plasmonic refractive index and temperature sensor based on square ring shape resonator with nanorods defects. Opt. Quantum Electron. 2022, 54, 184. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Liu, X.; Tian, H.; Wang, J.; Cui, J.; Rohimah, S. Optical sensing based on multimode Fano resonances in metal-insulator-metal waveguide systems with X-shaped resonant cavities. Appl. Opt. 2021, 60, 5312–5319. [Google Scholar] [CrossRef]
- Rohimah, S.; Tian, H.; Wang, J.; Chen, J.; Li, J.; Liu, X.; Cui, J.; Hao, Y. Tunable multiple Fano resonances based on a plasmonic metal-insulator-metal structure for nano-sensing and plasma blood sensing applications. Appl. Opt. 2022, 61, 1275–1283. [Google Scholar] [CrossRef]
- Fu, H.X.; Li, S.L.; Wang, Y.L.; Song, G.; Zhang, P.F.; Wang, L.L.; Yu, L. Independently Tunable Ultrasharp Double Fano Resonances in Coupled Plasmonic Resonator System. IEEE Photonics J. 2018, 10, 2791612. [Google Scholar] [CrossRef]
- Zhou, C.; Huo, Y.P.; Guo, Y.Y.; Niu, Q.Q. Tunable Multiple Fano Resonances and Stable Plasmonic Band-Stop Filter Based on a Metal-Insulator-Metal Waveguide. Plasmonics 2021, 16, 1735–1743. [Google Scholar] [CrossRef]
- Jurich, G.; Sievers, S. Reply to “Comment on ‘Observation of an index-of-refraction-induced change in the Drude parameters of Ag films.’”. Phys. Rev. B. 1986, 34, 1322–1324. [Google Scholar] [CrossRef]
- Zhu, J.H.; Wang, Q.J.; Shum, P.; Huang, X.G. A Simple Nanometeric Plasmonic Narrow-Band Filter Structure Based on Metal-Insulator-Metal Waveguide. IEEE. Trans. Nanotechnol. 2011, 10, 1371–1376. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Z.; Wang, R.; Hai, Z.; Xue, C.; Zhang, W.; Yan, S. Refractive Index Sensor Based on Fano Resonances in Metal-Insulator-Metal Waveguides Coupled with Resonators. Sensors 2017, 17, 784. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Xu, Y.; Cao, J. Fano resonance sensing characteristics of MIM waveguide coupled Square Convex Ring Resonator with metallic baffle. Results Phys. 2019, 14, 102420. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Liu, X.; Rohimah, S.; Tian, H.; Qi, D. Fano resonance in a MIM waveguide with double symmetric rectangular stubs and its sensing characteristics. Opt. Commun. 2021, 482, 126563. [Google Scholar] [CrossRef]
- Xu, D.; Yan, S.; Yang, X.; Su, H.; Wu, X.; Hua, E. A Nanoscale Structure Based on a Ring With Matchstick-Shape Cavity for Glucose Concentration and Temperature Detection. IEEE Sens. J. 2021, 21, 4442–4450. [Google Scholar] [CrossRef]
- El-Khozondar, H.J.; Mahalakshmi, P.; El-Khozondar, R.J.; Ramanujam, N.R.; Amiri, I.S.; Yupapin, P. Design of one dimensional refractive index sensor using ternary photonic crystal waveguide for plasma blood samples applications. Physica. E 2019, 111, 29–36. [Google Scholar] [CrossRef]

| Reference | Waveguide Structure | Sensitivity |
|---|---|---|
| [12] | MIM waveguide with two silver baffles and a coupled ring cavity | 718 nm/RIU |
| [13] | MIM waveguide with tooth cavity-coupled ring splitting cavity | 1200 nm/RIU |
| [19] | MIM waveguide with a baffle and a circular split-ring resonator cavity | 1114 nm/RIU |
| [24] | Two side-coupled semi-ring cavities and a vertical cavity | 1405 nm/RIU |
| [30] | Square Convex Ring Resonator (SCRR) with single metallic baffle | 1120 nm/RIU |
| [33] | Side-coupled rectangular cavity and rightward-opening semi-ring cavity | 1550 nm/RIU |
| [42] | Circular split-ring resonance cavity and double symmetric rectangular cavity | 1180 nm/RIU |
| [43] | MIM waveguides coupled with double rectangular cavities | 596 nm/RIU |
| This paper | MIM waveguide structure with square ring and triangular cavities | 2260 nm/RIU |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Tian, H.; Liu, X.; Li, J.; Liu, Y. Multiparameter Sensing Based on Tunable Fano Resonances in MIM Waveguide Structure with Square-Ring and Triangular Cavities. Photonics 2022, 9, 291. https://doi.org/10.3390/photonics9050291
Wang M, Tian H, Liu X, Li J, Liu Y. Multiparameter Sensing Based on Tunable Fano Resonances in MIM Waveguide Structure with Square-Ring and Triangular Cavities. Photonics. 2022; 9(5):291. https://doi.org/10.3390/photonics9050291
Chicago/Turabian StyleWang, Mingyu, He Tian, Xing Liu, Jina Li, and Yajie Liu. 2022. "Multiparameter Sensing Based on Tunable Fano Resonances in MIM Waveguide Structure with Square-Ring and Triangular Cavities" Photonics 9, no. 5: 291. https://doi.org/10.3390/photonics9050291
APA StyleWang, M., Tian, H., Liu, X., Li, J., & Liu, Y. (2022). Multiparameter Sensing Based on Tunable Fano Resonances in MIM Waveguide Structure with Square-Ring and Triangular Cavities. Photonics, 9(5), 291. https://doi.org/10.3390/photonics9050291






