Angle-Dependent Magic Optical Trap for the 6S1/2↔nP3/2 Rydberg Transition of Cesium Atoms
Abstract
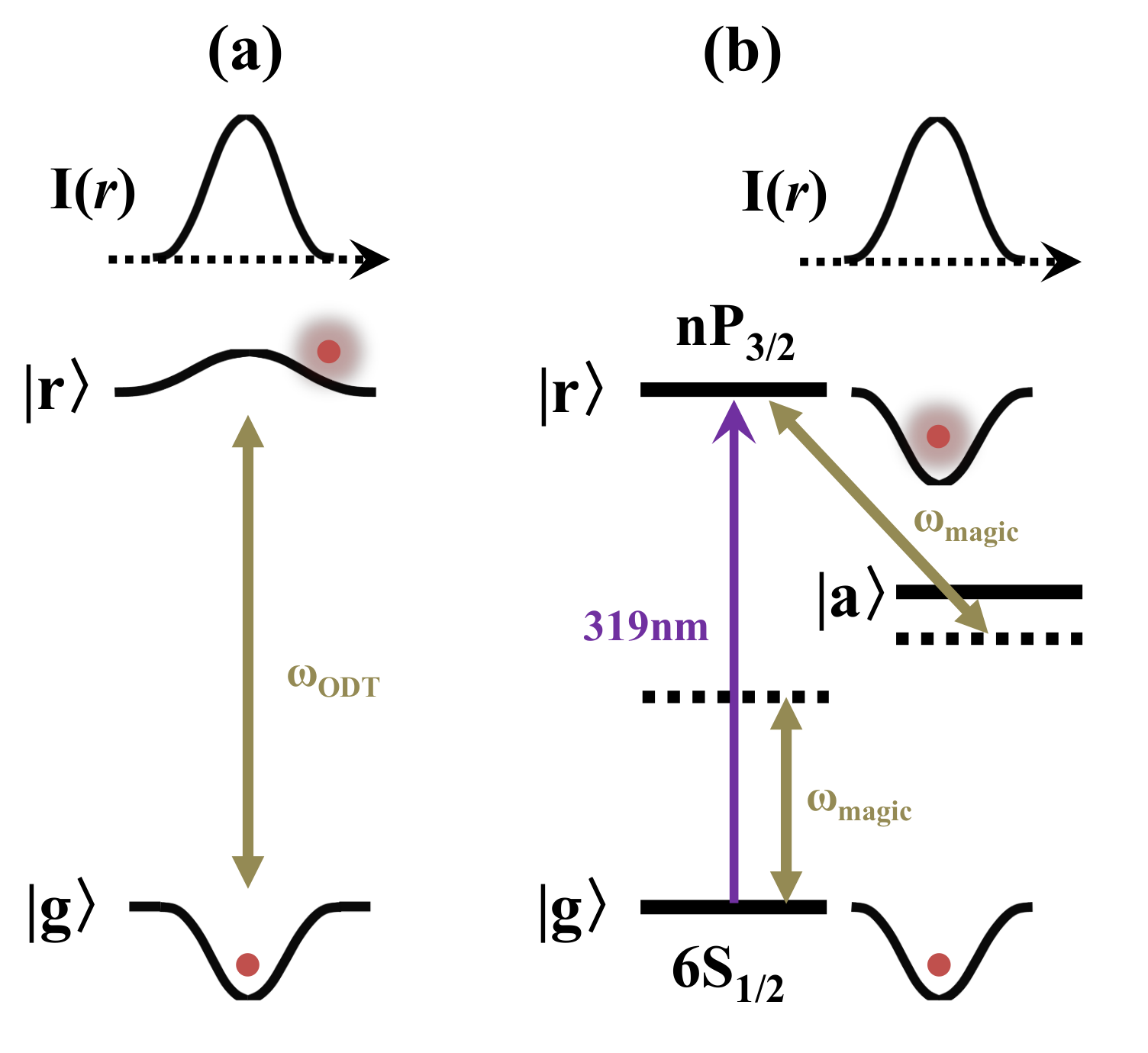
:1. Introduction
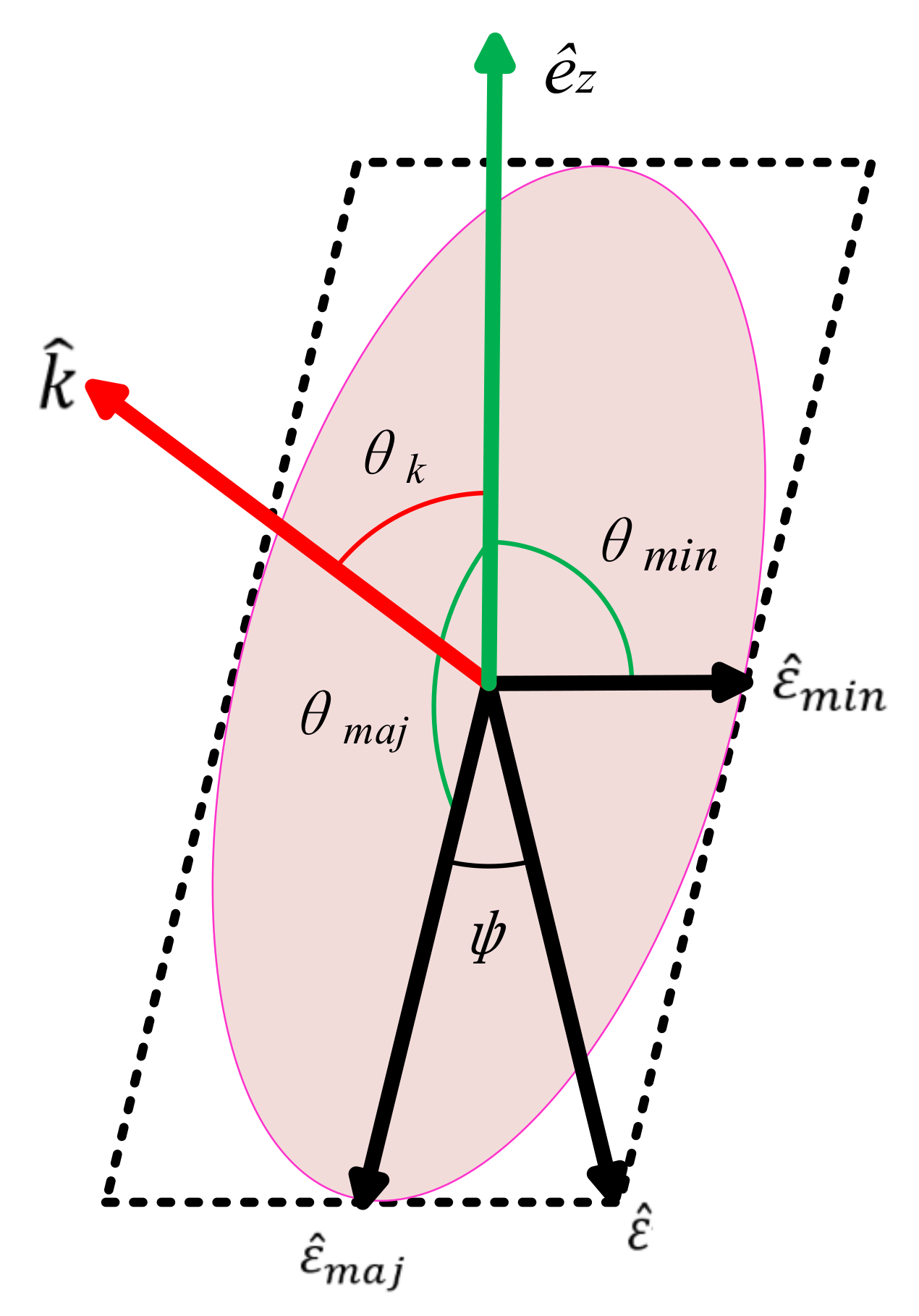
2. Calculation Methods
3. Results and Discussion
3.1. Magic Condition for Cs Ground State and Rydberg State
3.2. Magic Trapping Condition for Cs Rydberg States
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gallagher, T.F. Rydberg Atoms; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313–2363. [Google Scholar] [CrossRef]
- Adams, C.S.; Pritchard, J.D.; Shaffer, J.P. Rydberg atom quantum technologies. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 012002. [Google Scholar] [CrossRef] [Green Version]
- Browaeys, A.; Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 2020, 16, 132–142. [Google Scholar] [CrossRef]
- Dudin, Y.O.; Kuzmich, A. Strongly interacting Rydberg excitations of a cold atomic gas. Science 2012, 336, 887. [Google Scholar] [CrossRef]
- Ripka, F.; Kübler, H.; Löw, R.; Pfau, T. A room-temperature single-photon source based on strongly interacting Rydberg atoms. Science 2018, 362, 446–449. [Google Scholar] [CrossRef] [Green Version]
- Gorniaczyk, H.; Tresp, C.; Schmidt, J.; Fedder, H.; Hofferberth, S. Single-photon transistor mediated by interstate Rydberg interactions. Phys. Rev. Lett. 2014, 113, 053601. [Google Scholar] [CrossRef] [Green Version]
- Urban, E.; Johnson, T.A.; Henage, T.; Isenhower, L.; Yavuz, D.D.; Walker, T.G.; Saffman, M. Observation of Rydberg blockade between two atoms. Nat. Phys. 2009, 5, 110–114. [Google Scholar] [CrossRef]
- Sun, L.N.; Yan, L.L.; Su, S.L.; Jia, Y. One-step implementation of time-optimal-control three-qubit nonadiabatic holonomic controlled gates in Rydberg atoms. Phys. Rev. Appl. 2021, 16, 064040. [Google Scholar] [CrossRef]
- Grimm, R.; Weidemüller, M.; Ovchinnikov, Y.B. Optical dipole traps for neutral atoms. Adv. At. Mol. Opt. Phys. 2000, 42, 95–170. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.H.; Guest, J.R.; Povilus, A.P.; Hansis, E.; Raithel, G. Magnetic trapping of long-lived cold Rydberg atoms. Phys. Rev. Lett. 2005, 95, 243001. [Google Scholar] [CrossRef]
- Boetes, A.G.; Skannrup, R.V.; Naber, J.; Kokkelmans, S.J.J.M.F.; Spreeuw, R.J.C. Trapping of Rydberg atoms in tight magnetic microtraps. Phys. Rev. A 2018, 97, 013430. [Google Scholar] [CrossRef] [Green Version]
- Hogan, S.D.; Merkt, F. Demonstration of three-dimensional electrostatic trapping of state-selected Rydberg atoms. Phys. Rev. Lett. 2008, 100, 043001. [Google Scholar] [CrossRef] [Green Version]
- Anderson, S.E.; Younge, K.C.; Raithel, G. Trapping Rydberg atoms in an optical lattice. Phys. Rev. Lett. 2011, 107, 263001. [Google Scholar] [CrossRef]
- Barredo, D.; Lienhard, V.; Scholl, P.; de Léséleuc, S.; Boulier, T.; Browaeys, A.; Lahaye, T. Three-dimensional trapping of individual Rydberg atoms in ponderomotive bottle beam traps. Phys. Rev. Lett. 2020, 124, 023201. [Google Scholar] [CrossRef] [Green Version]
- Cortiñas, R.G.; Favier, M.; Ravon, B.; Méhaignerie, P.; Machu, Y.; Raimond, J.M.; Sayrin, C.; Brune, M. Laser trapping of circular Rydberg atoms. Phys. Rev. Lett. 2020, 124, 123201. [Google Scholar] [CrossRef] [Green Version]
- McKeever, J.; Buck, J.R.; Boozer, A.D.; Kuzmich, A.; Nagerl, H.C.; Stamper-Kurn, D.M.; Kimble, H.J. State-insensitive cooling and trapping of single atoms in an optical cavity. Phys. Rev. Lett. 2003, 90, 133602. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Dudin, Y.O.; Kuzmich, A. Entanglement between light and an optical atomic excitation. Nature 2013, 498, 466–469. [Google Scholar] [CrossRef]
- Bai, J.D.; Liu, S.; He, J.; Wang, J.M. Towards implementation of a magic optical-dipole trap for confining ground-state and Rydberg-state cesium cold atoms. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 155302. [Google Scholar] [CrossRef]
- Wilson, J.T.; Saskin, S.; Meng, Y.; Ma, S.; Dilip, R.; Burgers, A.P.; Thompson, J.D. Trapping alkaline earth Rydberg atoms optical tweezer arrays. Phys. Rev. Lett. 2022, 128, 033201. [Google Scholar] [CrossRef]
- Mei, Y.; Li, Y.; Nguyen, H.; Berman, P.; Kuzmich, A. Trapped alkali-metal Rydberg qubit. Phys. Rev. Lett. 2022, 128, 123601. [Google Scholar] [CrossRef]
- Wang, J.M.; Guo, S.L.; Ge, Y.L.; Cheng, Y.J.; Yang, B.D.; He, J. State-insensitive dichromatic optical-dipole trap for rubidium atoms: Calculation and the dicromatic laser’s realization. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 095001. [Google Scholar] [CrossRef]
- Liu, B.; Jin, G.; Sun, R.; He, J.; Wang, J.M. Measurement of magic-wavelength optical dipole trap by using the laser-induced fluorescence spectra of trapped single cesium atoms. Opt. Express 2017, 25, 15861–15867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zimmerman, M.L.; Littman, M.G.; Kash, M.M.; Kleppner, D. Stark structure of the Rydberg states of alkali-metal atoms. Phys. Rev. A 1979, 20, 2251–2275. [Google Scholar] [CrossRef]
- Kien, F.L.; Schneeweiss, P.; Rauschenbeutel, A. Dynamical polarizability of atoms in arbitrary light fields: General theory and application to cesium. Eur. Phys. J. D 2013, 67, 92. [Google Scholar] [CrossRef] [Green Version]
- Šibalić, N.; Pritchard, J.D.; Adams, C.S.; Weatherill, K.J. ARC: An open-source library for calculating properties of alkali Rydberg atoms. Comput. Phys. Commun. 2017, 220, 319–331. [Google Scholar] [CrossRef]
- Mitroy, J.; Safronova, M.S.; Clark, C.W. Theory and applications of atomic and ionic polarizabilities. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 202001. [Google Scholar] [CrossRef]
- Younge, K.C.; Anderson, S.E.; Raithel, G. Adiabatic potentials for Rydberg atoms in a ponderomotive optical lattice. New J. Phys. 2010, 12, 023031. [Google Scholar] [CrossRef]
- Budker, D.; Kimball, D.; DeMille, D. Atomic Physics: An Exploration through Problems and Solutions; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Hankin, A.M.; Jau, Y.Y.; Parazzoli, L.P.; Chou, C.W.; Armstrong, D.J.; Landahl, A.J.; Biedermann, G.W. Two-atom Rydberg blockade using direct 6S to nP excitation. Phys. Rev. A 2014, 89, 033416. [Google Scholar] [CrossRef] [Green Version]
- Jau, Y.Y.; Hankin, A.M.; Keating, T.; Deutsch, I.H.; Biedermann, G.W. Entangling atomic spins with a Rydberg-dressed spin-flip blockade. Nat. Phys. 2015, 12, 71–74. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.Y.; Bai, J.D.; He, J.; Wang, J.M. Single-photon cesium Rydberg excitation spectroscopy using 318.6-nm UV laser and room-temperature vapor cell. Opt. Express 2017, 25, 22510–22518. [Google Scholar] [CrossRef] [Green Version]
- Bai, J.D.; Wang, J.Y.; Liu, S.; He, J.; Wang, J.M. Autler–Townes doublet in single-photon Rydberg spectra of cesium atomic vapor with a 319 nm UV laser. Appl. Phys. B 2019, 125, 33. [Google Scholar] [CrossRef] [Green Version]
- Bai, J.D.; Liu, S.; Wang, J.Y.; He, J.; Wang, J.M. Single-photon Rydberg excitation and trap-loss spectroscopy of cold cesium atoms in a magneto-optical trap by using of a 319-nm ultraviolet laser system. IEEE J. Sel. Top. Quant. Electr. 2020, 26, 1600106. [Google Scholar] [CrossRef] [Green Version]



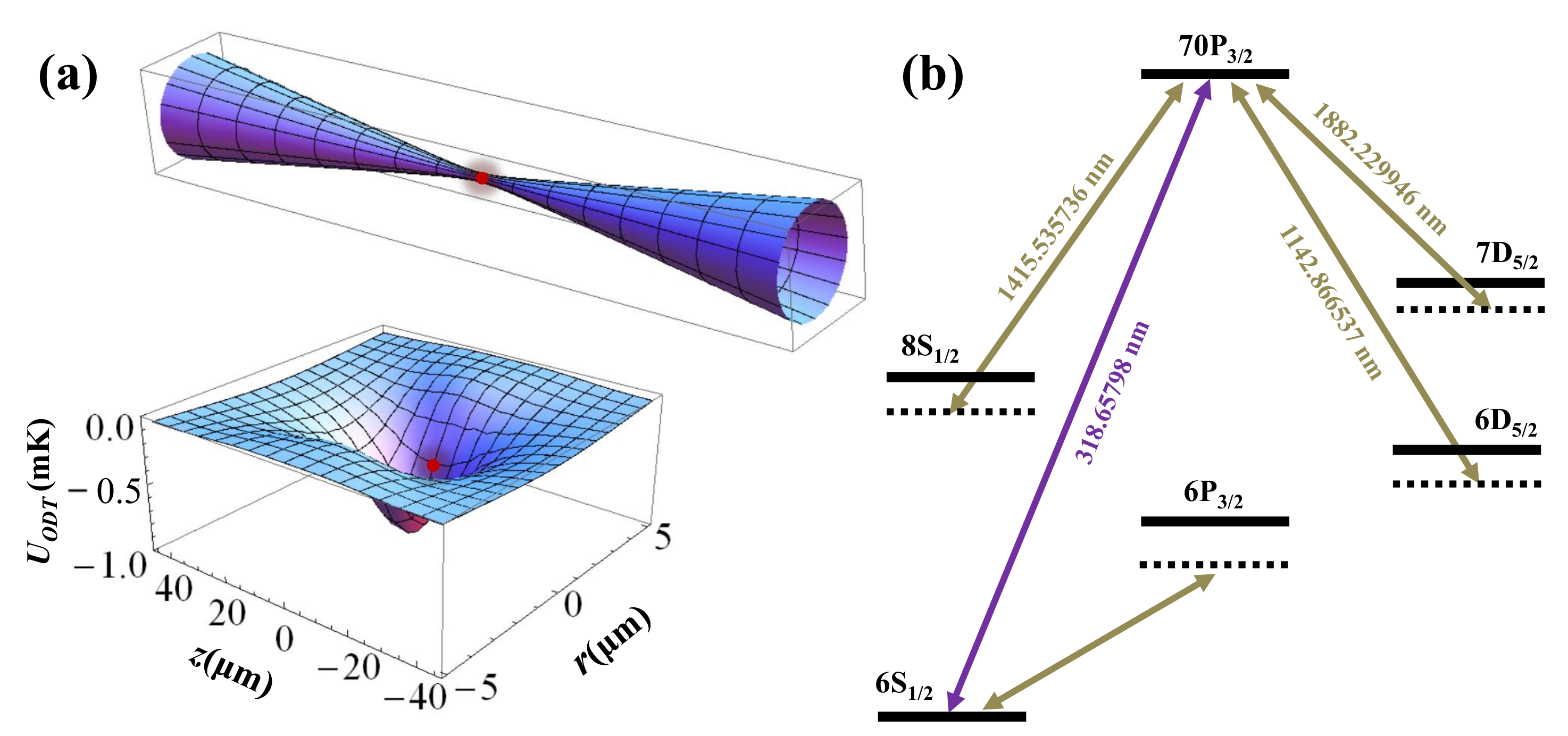

| Auxiliary Transition | Magic Detuning (MHz) | Magic Wavelength (nm) |
|---|---|---|
| 302.67 | 1882.229946 | |
| 77.08 | 1415.535736 | |
| 134.48 | 1142.866537 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Wang, X.; Hou, X.; Liu, W.; Wang, J. Angle-Dependent Magic Optical Trap for the 6S1/2↔nP3/2 Rydberg Transition of Cesium Atoms. Photonics 2022, 9, 303. https://doi.org/10.3390/photonics9050303
Bai J, Wang X, Hou X, Liu W, Wang J. Angle-Dependent Magic Optical Trap for the 6S1/2↔nP3/2 Rydberg Transition of Cesium Atoms. Photonics. 2022; 9(5):303. https://doi.org/10.3390/photonics9050303
Chicago/Turabian StyleBai, Jiandong, Xin Wang, Xiaokai Hou, Wenyuan Liu, and Junmin Wang. 2022. "Angle-Dependent Magic Optical Trap for the 6S1/2↔nP3/2 Rydberg Transition of Cesium Atoms" Photonics 9, no. 5: 303. https://doi.org/10.3390/photonics9050303
APA StyleBai, J., Wang, X., Hou, X., Liu, W., & Wang, J. (2022). Angle-Dependent Magic Optical Trap for the 6S1/2↔nP3/2 Rydberg Transition of Cesium Atoms. Photonics, 9(5), 303. https://doi.org/10.3390/photonics9050303





