Rapid Calibration of the Projector in Structured Light Systems Based on Brox Optical Flow Estimation
Abstract
:1. Introduction
- (a)
- The calibration is fast. Only two images before and after the motion of the calibration plate are required to calibrate the projector after the calibration of the camera;
- (b)
- High measurement accuracy. Although multiple images are recorded for calibration in traditional measurement methods, only dozens of feature points in each image are used as effective information points. However, in the proposed method, every pixel in the two images can be utilized as an information point, thus ensuring the accuracy of calibration results;
- (c)
- It is robust to noise because of the utilization of the Brox optical flow estimation algorithm in the calculation of the motion of each point between two images;
- (d)
- It is immunity from the non-uniform brightness distribution caused by the environment or by the lens distortion because the optical flow is calculated point-by-point.
2. Principles
2.1. Brox Optical Flow Estimation Algorithm
2.2. Principle of Camera Calibration
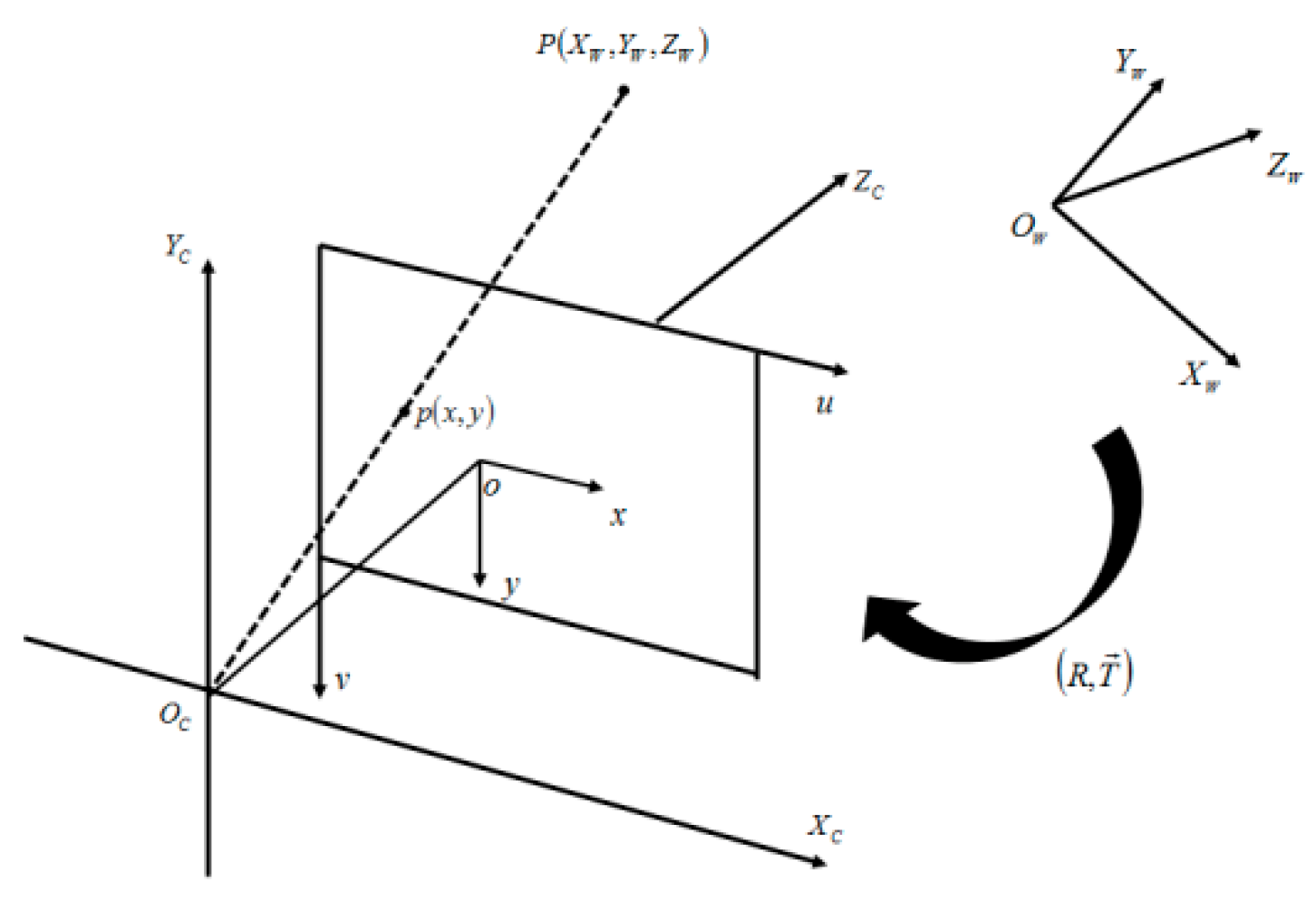
2.3. Principle of Projector Calibration
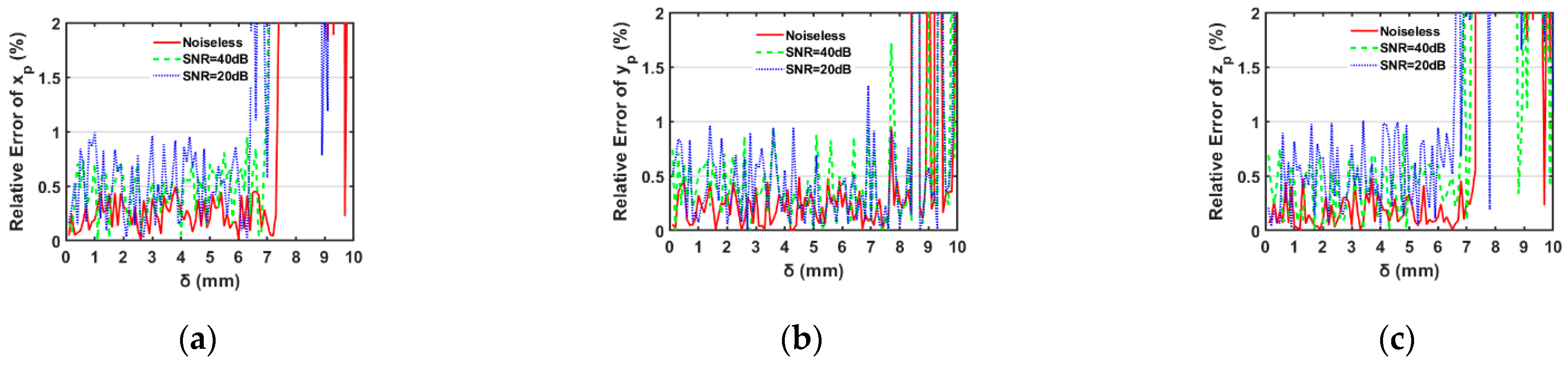
3. Numerical Simulations
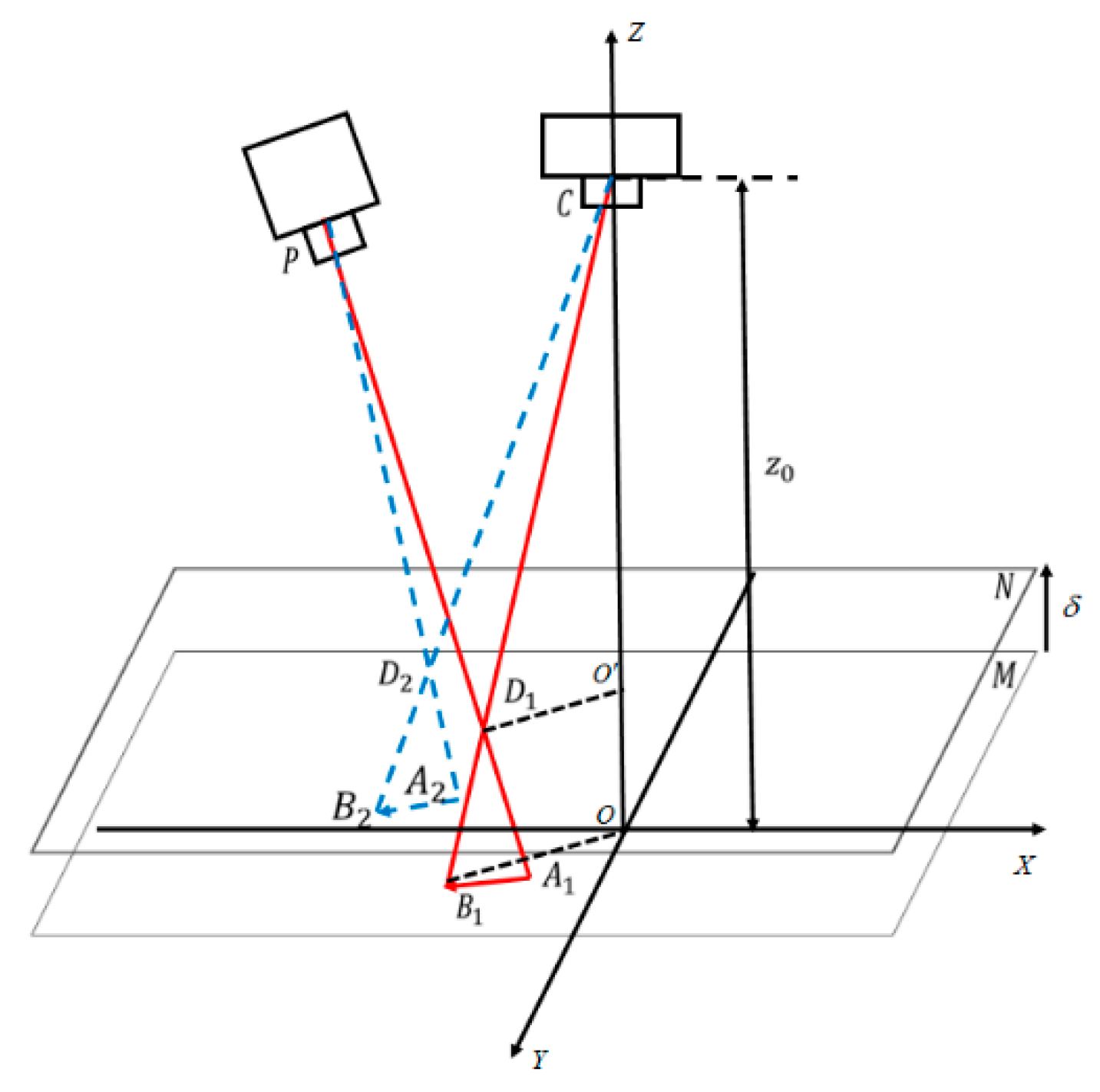
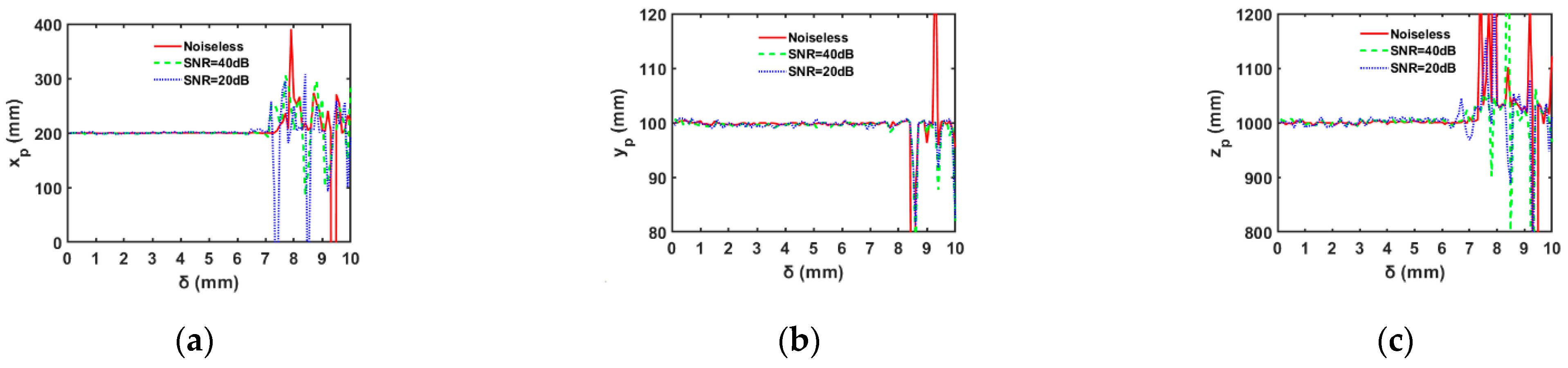
3.1. Range Estimation of Moving Distance of Calibration Plate
3.2. Projector Calibration
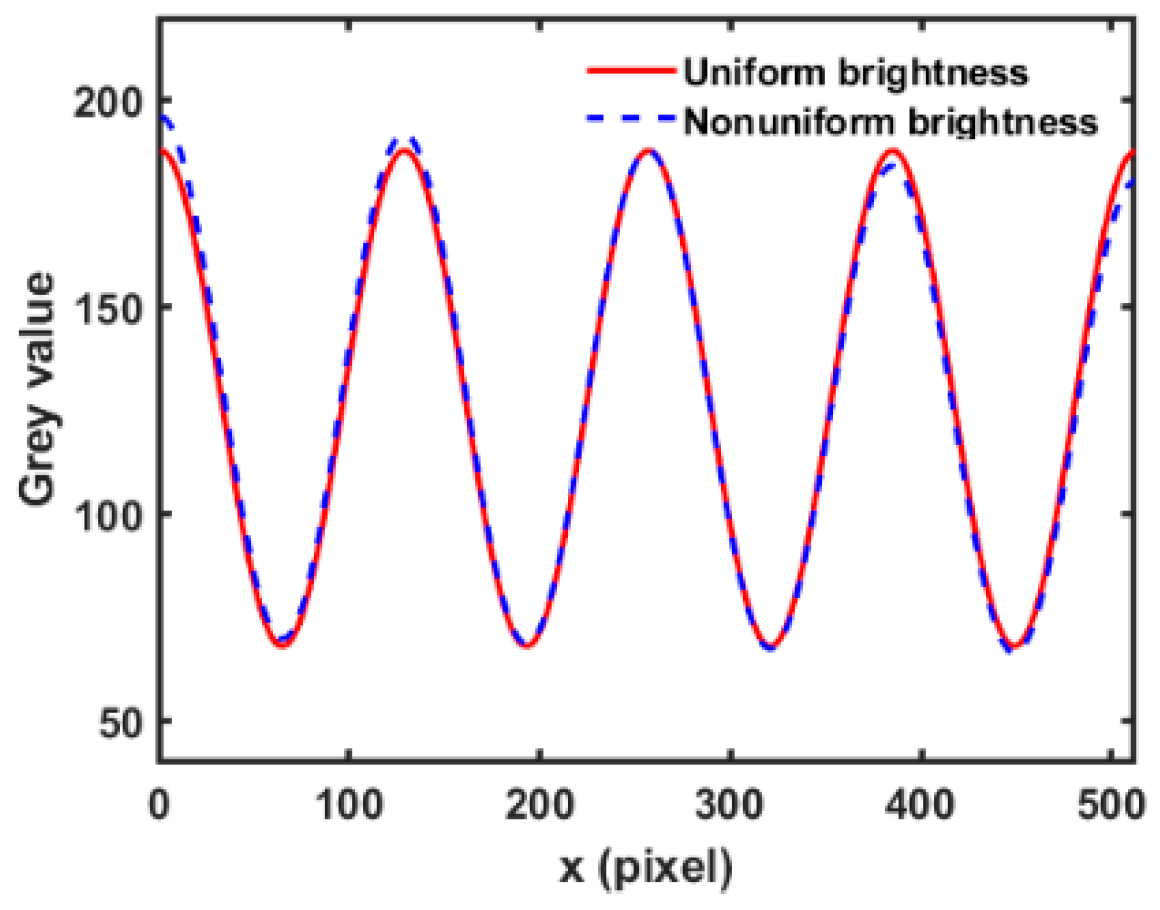
3.2.1. Projector Calibration with Uniform Brightness Pattern
3.2.2. Projector Calibration with Non-Uniform Brightness Pattern
3.3. Discussion of the Calibration
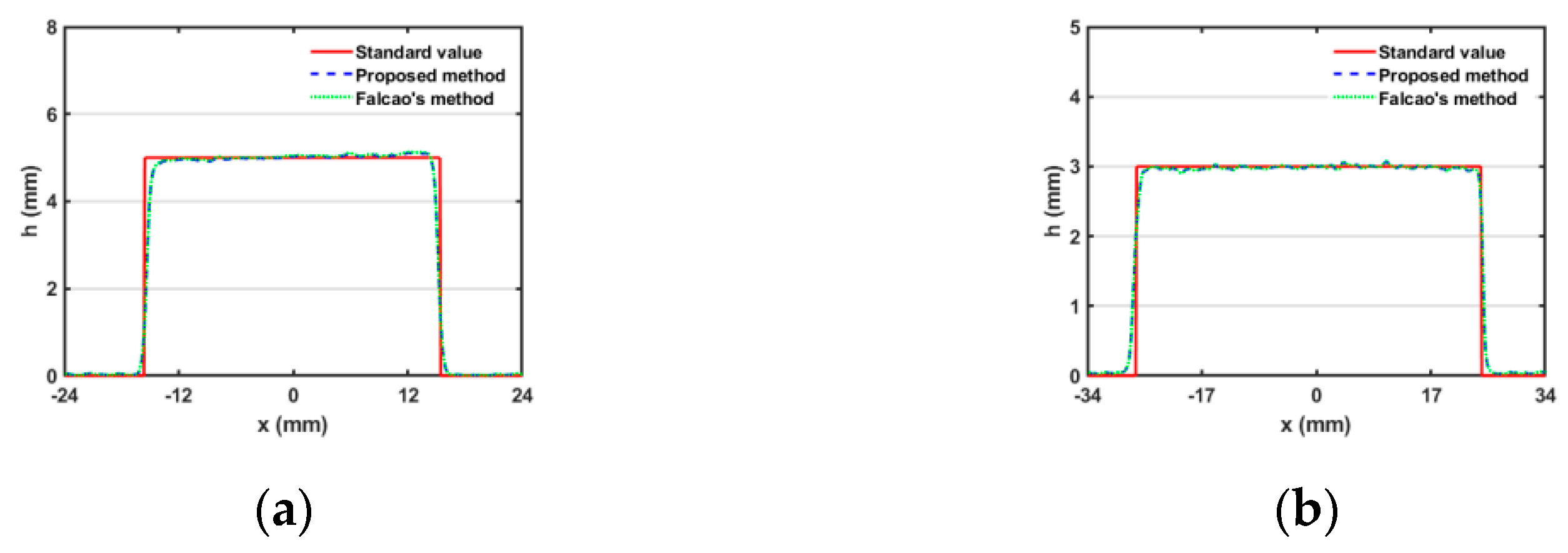
4. Experiment
- 1.
- The camera calibration is completed to obtain the image distance . This step can be completed by using the camera calibration toolbox with MATLAB;
- 2.
- The grid pattern generated according to Equation (13) is projected on the calibration plate. The first image captured by the camera is shown in Figure 13a, and the plane where the calibration plate is located is defined as the reference plane;
- 3.
- Move the platform and then capture the second image, as shown in Figure 13b, after estimating the motion range of the moving platform roughly according to Equation (12). If the calibration board moves toward the camera, the moving distance is defined as positive, and vice versa;
- 4.
- Calculate the optical flow between two images, and then the 3-D coordinates of the projector can be obtained using Equation (10).

5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Godin, G.; Beraldin, J.A.; Taylor, J.; Cournoyer, L.; Rioux, M.; El-Hakim, S.; Baribeau, R.; Blais, F.; Boulanger, P.; Domey, J.; et al. Active Optical 3D Imaging for Heritage Applications. IEEE Comput. Graph. Appl. 2002, 22, 24–36. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X. Application of 3D optical measurement system on quality inspection of turbine blade. In Proceedings of the 2009 16th International Conference on Industrial Engineering and Engineering Management, Beijing, China, 21–23 October 2009; pp. 1089–1092. [Google Scholar]
- Hung, Y.Y.; Lin, L.; Shang, H.M.; Park, B.G. Practical three-dimensional computer vision techniques for full-field surface measurement. Opt. Eng. 2000, 39, 143–149. [Google Scholar] [CrossRef]
- Fitts, J.M. High-Speed 3-D Surface Measurement Surface Inspection and Reverse-CAD System. U.S. Patent 5,175,601, 29 December 1992. [Google Scholar]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Figl, M.; Ede, C.; Hummel, J. A fully automated calibration method for an optical see-through head-mounted operating microscope with variable zoom and focus. IEEE Trans. Med. Imaging 2005, 24, 1492–1499. [Google Scholar] [CrossRef] [PubMed]
- Sarkis, M.; Senft, C.T.; Diepold, K. Calibrating an Automatic Zoom Camera with Moving Least Squares. IEEE Trans. Autom. Sci. Eng. 2009, 6, 492–503. [Google Scholar] [CrossRef]
- Huang, J.C.; Liu, C.S.; Tsai, C.Y. Calibration Procedure of Camera with Multifocus Zoom Lens for Three-Dimensional Scanning System. IEEE Access 2021, 9, 106387–106398. [Google Scholar] [CrossRef]
- Falcao, G.; Hurtos, N.; Massich, J. Plane-based calibration of a projector-camera system. VIBOT Master 2008, 9, 1–12. [Google Scholar]
- Fernandez, S.; Salvi, J. Planar-based camera-projector calibration. In Proceedings of the 7th International Symposium on Image and Signal Processing and Analysis, Dubrovnik, Croatia, 4–6 September 2011. [Google Scholar]
- Huang, Z.; Xi, J.; Yu, Y.; Guo, Q. Accurate projector calibration based on a new point-to-point mapping relationship between the camera and projector images. Appl. Opt. 2015, 54, 347–356. [Google Scholar] [CrossRef]
- Li, B.W.; Zhang, S. Flexible calibration method for microscopic structured light system using telecentric lens. Opt. Express 2015, 23, 25795. [Google Scholar] [CrossRef]
- Nacolas, V.J.; Arnaldo, L.J.; Leticia, A.; Laura, V.V.; Pablo, C.R.; Andres, A.R.D.; Mariana, L.; Carlos, M.; Teodiano, B.; Anselmo, F. A Comparative Study of Markerless Systems Based on Color-Depth Cameras, Polymer Optical Fiber Curvature Sensors, and Inertial Measurement Units: Towards Increasing the Accuracy in Joint Angle Estimation. Electronics 2019, 8, 173. [Google Scholar]
- Zhang, S.; Huang, P.S. Novel method for structured light system calibration. Opt. Eng. 2006, 45, 083601. [Google Scholar]
- Peng, J.; Liu, X.; Deng, D.; Guo, H.; Cai, Z.; Peng, X. Suppression of projector distortion in phase-measuring profilometry by projecting adaptive fringe patterns. Opt. Express 2016, 24, 21846. [Google Scholar] [CrossRef]
- Yang, S.; Liu, M.; Song, J.; Yin, S.; Ren, Y.; Zhu, J. Projector distortion residual compensation in fringe projection system. Opt. Lasers Eng. 2019, 114, 104–110. [Google Scholar] [CrossRef]
- Yang, S.; Liu, M.; Song, J.; Yin, S.; Guo, Y.; Ren, Y.; Zhu, J. Flexible digital projector calibration method based on per-pixel distortion measurement and correction. Opt. Lasers Eng. 2017, 92, 29–38. [Google Scholar] [CrossRef]
- Lei, Z.F.; Sun, P.; Hu, C.H. The sensitivity and the measuring range of the typical differential optical flow method for displacement measurement using the fringe pattern. Opt. Commun. 2021, 487, 126806. [Google Scholar] [CrossRef]
- Javh, J.; Slavič, J.; Boltežar, M. The subpixel resolution of optical-flow-based modal analysis. Mech. Syst. Signal Process. 2017, 88, 89–99. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the 7th International Joint Conference on ArtificialIntelligence, Lausanne, Switzerland, 8–10 October 1997; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1997. [Google Scholar]
- Brox, T.; Bruhn, A.; Papenberg, N.; Weickert, J. High accuracy optical flow estimation based on a theory for warping. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 25–36. [Google Scholar]
- Sun, P.; Dai, Q.; Tang, Y.X.; Lei, Z.F. Coordinate calculation for direct shape measurement based on optical flow. Appl. Opt. 2020, 59, 92. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.X.; Sun, P.; Dai, Q.; Fan, C.; Lei, Z.F. Object shape measurement based on Brox optical flow estimation and its correction method. Photonics 2020, 7, 109. [Google Scholar] [CrossRef]
- Zhao, R.; Li, X.; Sun, P. An improved windowed Fourier transform filter algorithm. Opt. Laser Technol. 2015, 74, 103–107. [Google Scholar] [CrossRef]









Relative Error (%) | Relative Error (%) | Relative Error (%) | ||||
|---|---|---|---|---|---|---|
| 1000.00/7.00 | 200.33 | 0.17 | 100.05 | 0.05 | 1003.78 | 0.38 |
| 1005.00/7.10 | 201.26 | 0.63 | 100.14 | 0.14 | 1007.12 | 0.71 |
| 995.00/6.90 | 199.34. | 0.33 | 100.77 | 0.77 | 993.54 | 0.65 |
| 1005.00/6.90 | 198.41 | 0.80 | 100.24 | 0.24 | 991.24 | 0.88 |
| 995.00/7.10 | 202.34 | 1.90 | 100.65 | 0.65 | 1009.71 | 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Sun, P.; Zhang, H.; Shao, N.; Zhao, R. Rapid Calibration of the Projector in Structured Light Systems Based on Brox Optical Flow Estimation. Photonics 2022, 9, 375. https://doi.org/10.3390/photonics9060375
Tang Y, Sun P, Zhang H, Shao N, Zhao R. Rapid Calibration of the Projector in Structured Light Systems Based on Brox Optical Flow Estimation. Photonics. 2022; 9(6):375. https://doi.org/10.3390/photonics9060375
Chicago/Turabian StyleTang, Yuxin, Ping Sun, Hua Zhang, Nan Shao, and Ran Zhao. 2022. "Rapid Calibration of the Projector in Structured Light Systems Based on Brox Optical Flow Estimation" Photonics 9, no. 6: 375. https://doi.org/10.3390/photonics9060375
APA StyleTang, Y., Sun, P., Zhang, H., Shao, N., & Zhao, R. (2022). Rapid Calibration of the Projector in Structured Light Systems Based on Brox Optical Flow Estimation. Photonics, 9(6), 375. https://doi.org/10.3390/photonics9060375




