Dual Polarization Simultaneous Optical Intensity Modulation in Single Birefringent LiNbO3 Mach–Zehnder Optical Modulator
Abstract
:1. Introduction
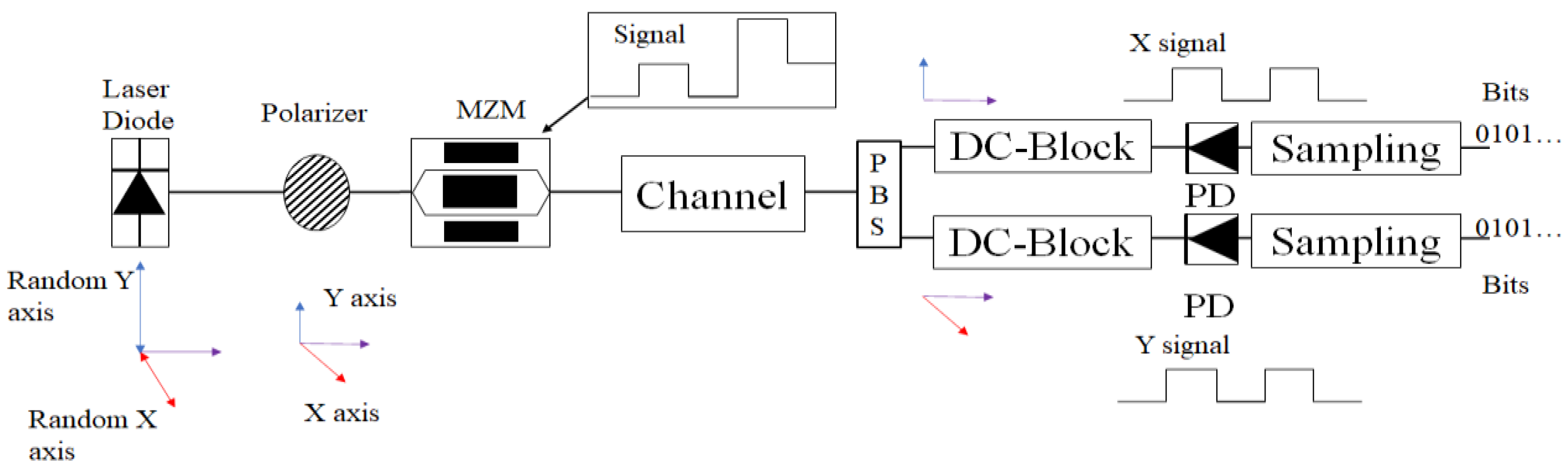
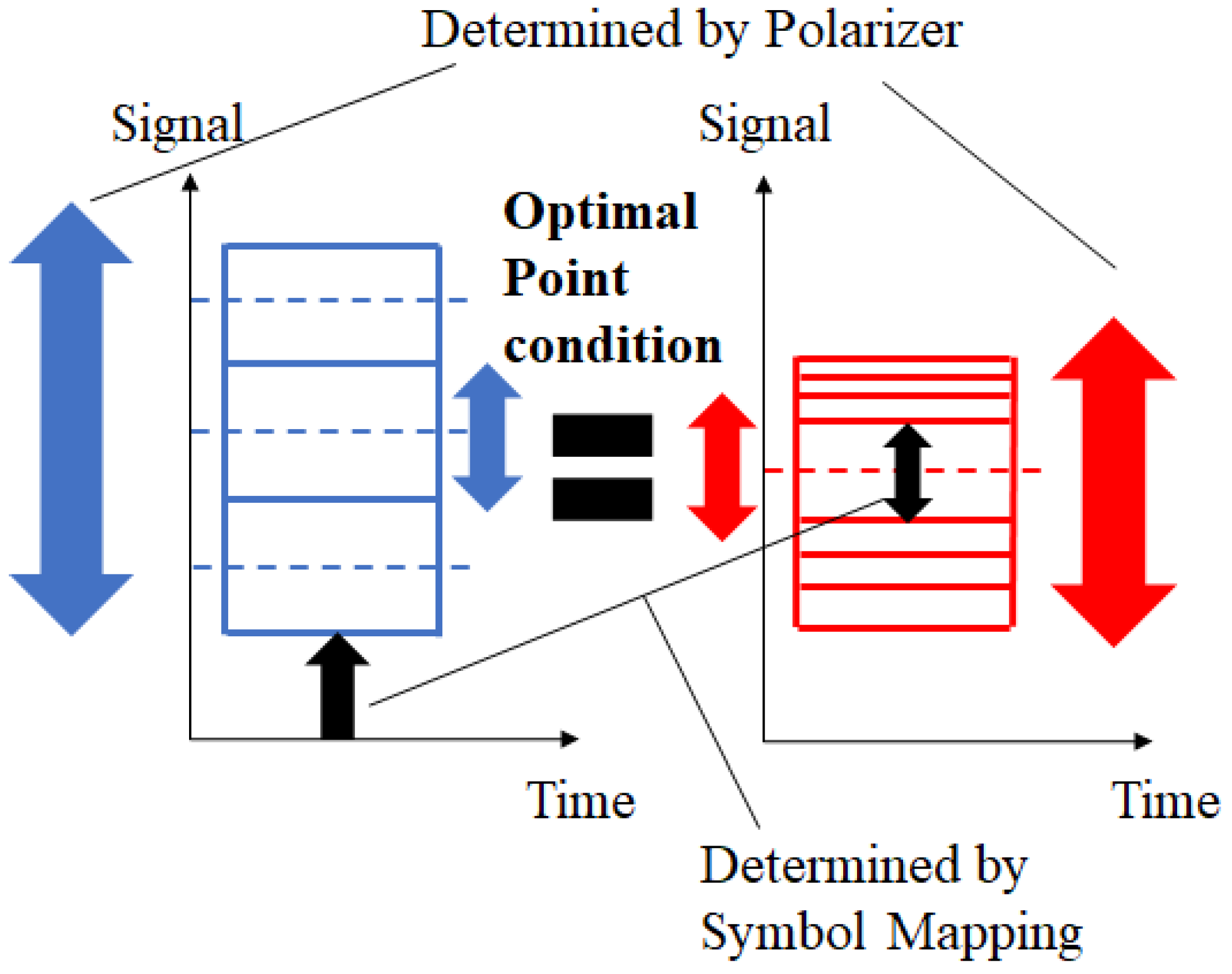
2. Schematics
3. Simulation and Experimental Results
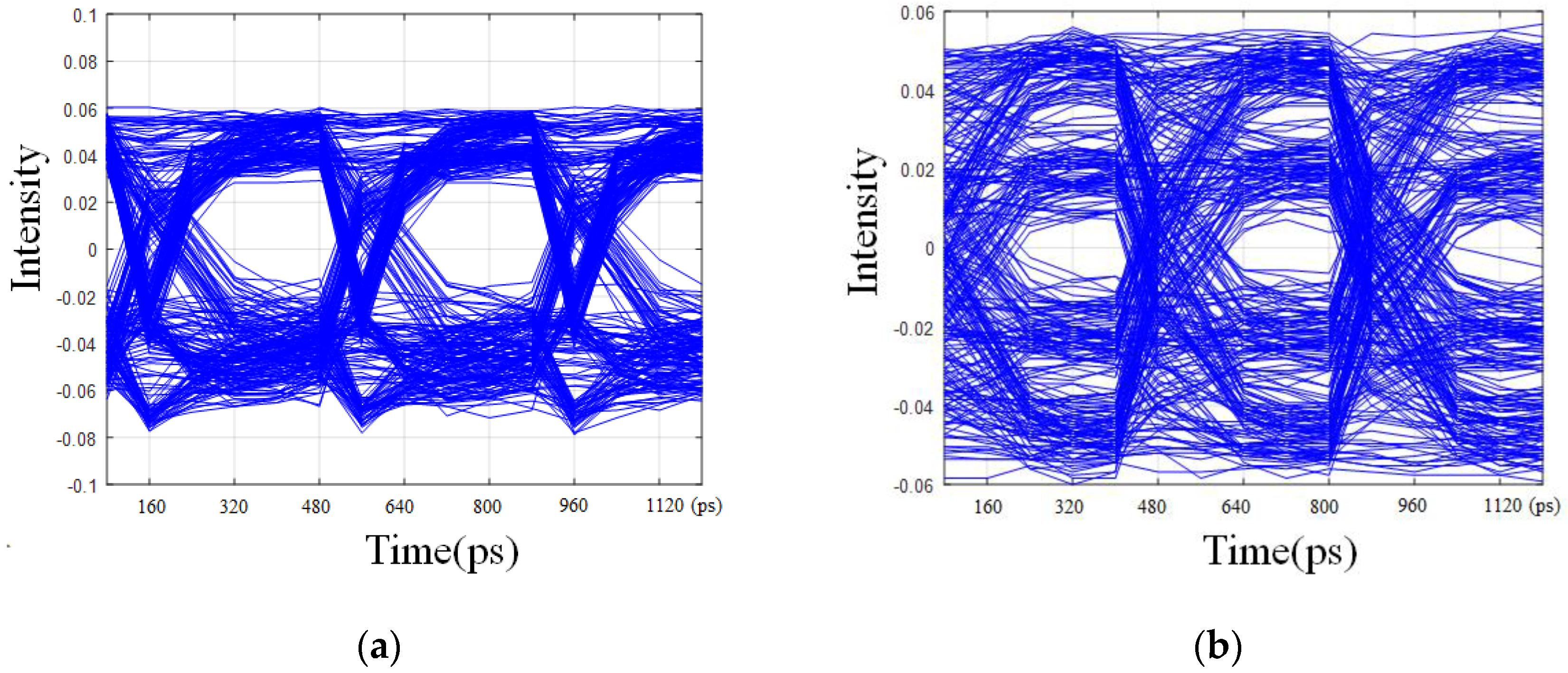
3.1. Simulation
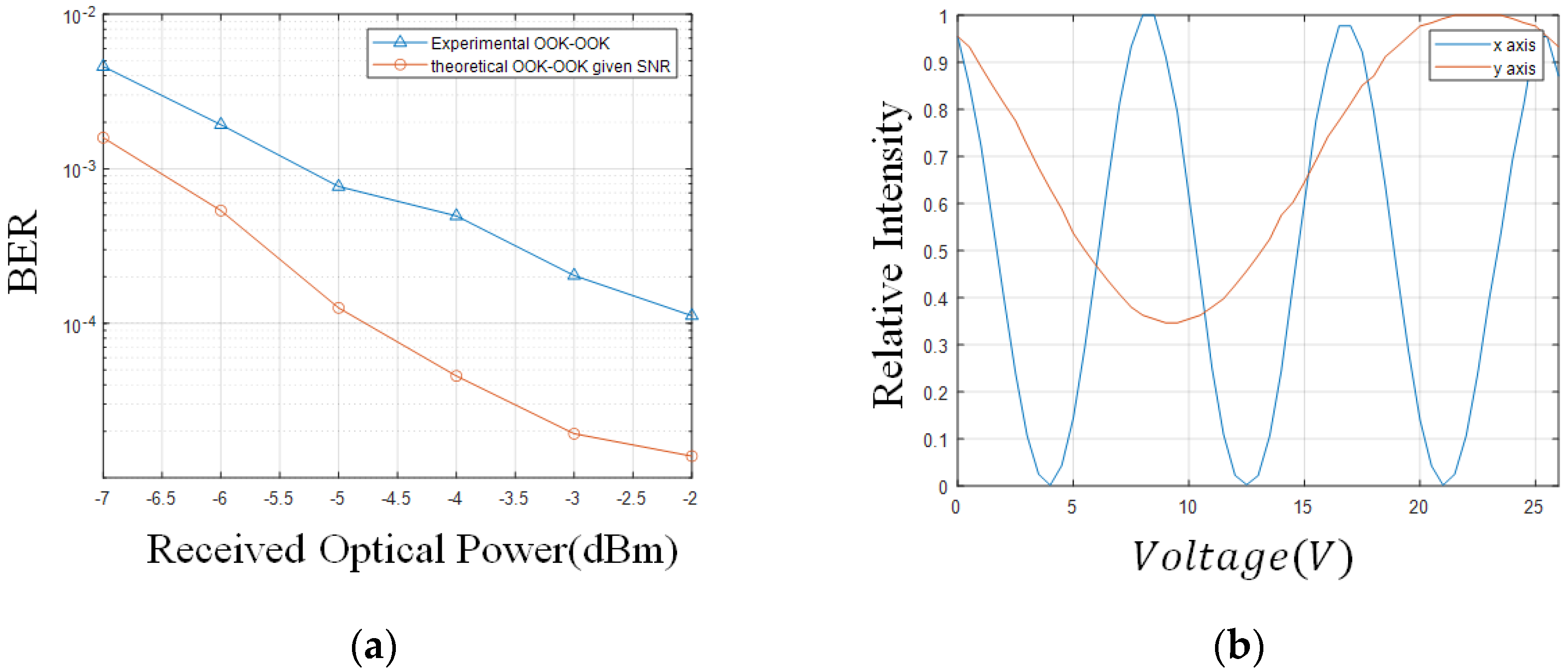
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, H.J.; Ha, I.H.; Kang, S.M.; Shin, W.H.; Han, S.K. 3D QAM-DPSK Optical Transmission Employing a Single Mach–Zehnder Modulator and Optical Direct Detection. J. Lightwave Technol. 2020, 38, 6247–6256. [Google Scholar] [CrossRef]
- Hong, Y.-Q.; Han, S.-K. Polarization-dependent SOA-based PolSK modulation for turbulence-robust FSO communication. Opt. Express 2021, 29, 15587–15594. [Google Scholar] [CrossRef] [PubMed]
- Luan, H.; Lin, D.; Li, K.; Meng, W.; Gu, M.; Fang, X. 768-ary Laguerre-Gaussian-mode shift keying free-space optical communication based on convolutional neural networks. Opt. Express 2021, 29, 19807–19818. [Google Scholar] [CrossRef] [PubMed]
- Sivakumar, P.; Boopathi, C.S.; Sumithra, M.G.; Singh, M.; Malhotra, J.; Grover, A. Ultra-high capacity long-haul PDM-16-QAM-based WDM-FSO transmission system using coherent detection and digital signal processing. Opt. Quantum Electron. 2020, 52, 500. [Google Scholar] [CrossRef]
- Muga, N.J.; Fernandes, G.M.; Ziaie, S.; Ferreira, R.M.; Shahpari, A.; Teixeira, A.L.; Pinto, A.N. Advanced digital signal processing techniques based on Stokes space analysis for high-capacity coherent optical systems. In Proceedings of the 19th International Conference on Transparent Optical Networks (ICTON 2017), Girona, Spain, 2–6 July 2017; pp. 1–5. [Google Scholar]
- Mun, K.-H.; Kang, S.-M.; Han, S.-K. Multiple-Noise-Tolerant CO-OFDMA-PON Uplink Multiple Access Using AM-DAPSK-OFDM With Reflective ONUs. J. Light. Technol. 2018, 36, 5462–5469. [Google Scholar] [CrossRef]
- Ohm, M.; Speidel, J. Quaternary optical ASK-DPSK and receivers with direct detection. IEEE Photon-Technol. Lett. 2003, 15, 159–161. [Google Scholar] [CrossRef]
- Jung, S.-M.; Mun, K.-H.; Kang, S.-M.; Han, S.-K. Wavelength reused bidirectional reflective coherent-PON based on cascaded SOA/RSOA ONUs. Opt. Fiber Technol. 2018, 45, 289–294. [Google Scholar] [CrossRef]
- Seimetz, M.; Noelle, M.; Patzak, E. Optical systems with high-order DPSK and star QAM modulation based on interferometric direct detection. J. Lightwave Technol. 2007, 25, 1515–1530. [Google Scholar] [CrossRef]
- Wang, P.; Xiong, W.; Huang, Z.; He, Y.; Liu, J.; Ye, H.; Xiao, J.; Li, Y.; Fan, D.; Chen, S. Diffractive Deep Neural Network for Optical Orbital Angular Momentum Multiplexing and Demultiplexing. IEEE J. Sel. Top. Quantum Electron. 2021, 28, 1–11. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, Z.; Xie, G.; Li, L.; Cao, Y.; Liu, C.; Liao, P.; Yan, Y.; Ahmed, N.; Zhao, Z.; et al. Free-space optical communications using orbital-angular-momentum multiplexing combined with MIMO-based spatial multiplexing. Opt. Lett. 2015, 40, 4210–4213. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Wang, J. Supermode fiber for orbital angular momentum (OAM) transmission. Opt. Express 2015, 23, 18736–18745. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Li, G. Direct detection differential polarization-phase-shift keying based on Jones vector. Opt. Express 2004, 12, 5821–5826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prabu, K.; Kumar, D.S. MIMO free-space optical communication employing coherent BPOLSK modulation in atmospheric optical turbulence channel with pointing errors. Opt. Commun. 2015, 343, 188–194. [Google Scholar] [CrossRef]
- Wong, K.K. Properties of Lithium Niobate; INSPEC: London, UK, 2002. [Google Scholar]
- Hu, E.; Hsueh, Y.; Wong, K.; Marhic, M.; Kazovsky, L.; Shimizu, K.; Kikuchi, N. 4-level direct-detection polarization shift-keying (DD-PolSK) system with phase modulators. In Proceedings of the OFC 2003 Optical Fiber Communications Conference, San Diego, CA, USA, 26 March 2003; IEEE: New York, NY, USA, 2003; Volume 2, pp. 647–649. [Google Scholar]
- Sklar, B. Digital Communications: Fundamentals and Applications; Prentics Hall: Hoboken, NJ, USA, 2001. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyun, Y.-J.; Choi, J.-Y.; Han, S.-K. Dual Polarization Simultaneous Optical Intensity Modulation in Single Birefringent LiNbO3 Mach–Zehnder Optical Modulator. Photonics 2022, 9, 386. https://doi.org/10.3390/photonics9060386
Hyun Y-J, Choi J-Y, Han S-K. Dual Polarization Simultaneous Optical Intensity Modulation in Single Birefringent LiNbO3 Mach–Zehnder Optical Modulator. Photonics. 2022; 9(6):386. https://doi.org/10.3390/photonics9060386
Chicago/Turabian StyleHyun, Young-Jin, Jae-Young Choi, and Sang-Kook Han. 2022. "Dual Polarization Simultaneous Optical Intensity Modulation in Single Birefringent LiNbO3 Mach–Zehnder Optical Modulator" Photonics 9, no. 6: 386. https://doi.org/10.3390/photonics9060386
APA StyleHyun, Y.-J., Choi, J.-Y., & Han, S.-K. (2022). Dual Polarization Simultaneous Optical Intensity Modulation in Single Birefringent LiNbO3 Mach–Zehnder Optical Modulator. Photonics, 9(6), 386. https://doi.org/10.3390/photonics9060386





