Combined Non-Invasive Optical Oximeter and Flowmeter with Basic Metrological Equipment
Abstract
:1. Introduction
2. Substantiation of Advantages to Develop a Multifunctional Oximeter
- The extension of a set of measured parameters;
- The substantiation of a number of the most important technical design parameters;
- The development of the initial tool for metrological tuning of measuring channels.
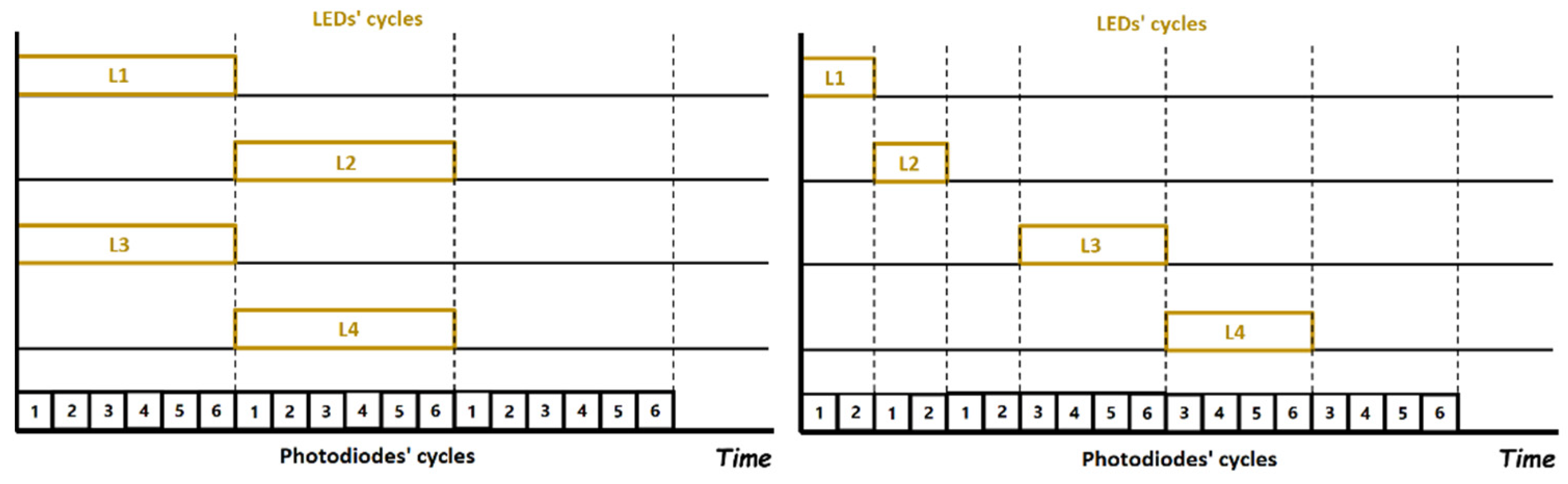
3. The Multifunctional Oximeter Design
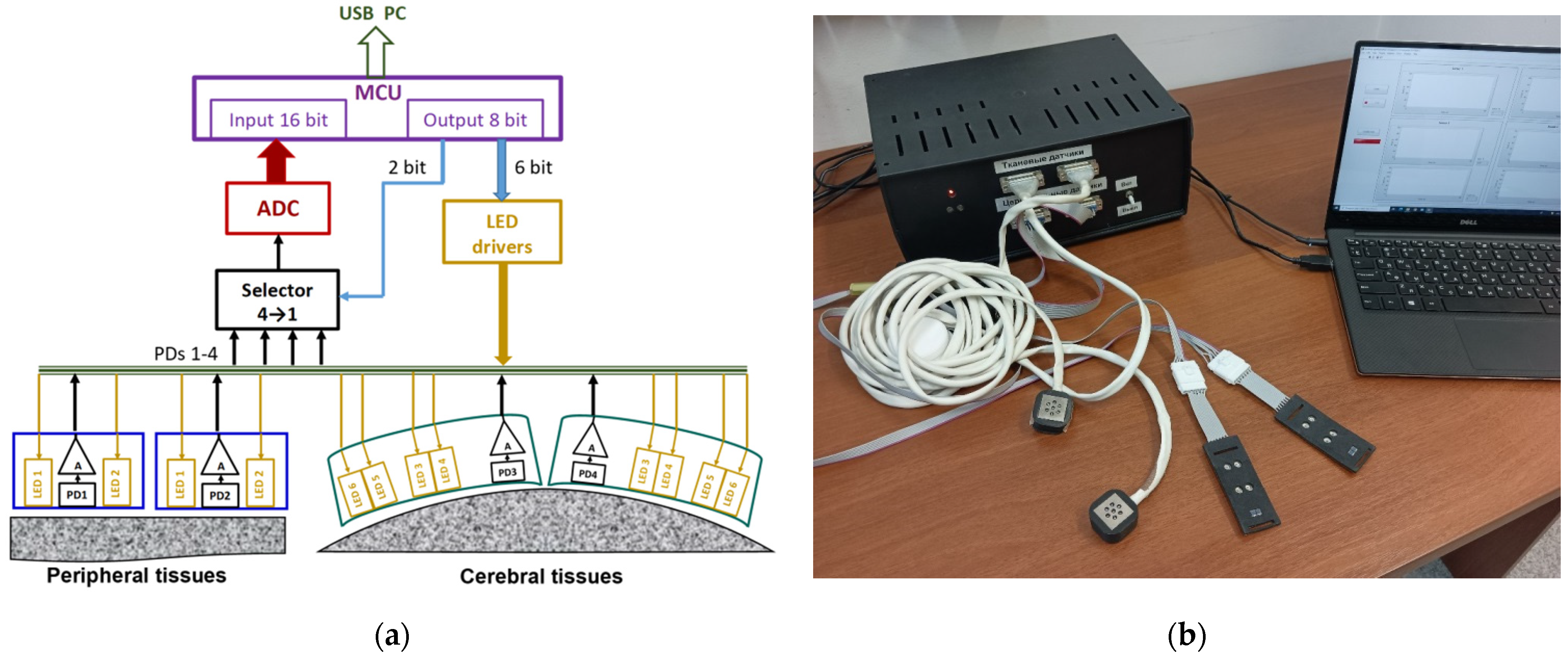
3.1. The System as a Whole
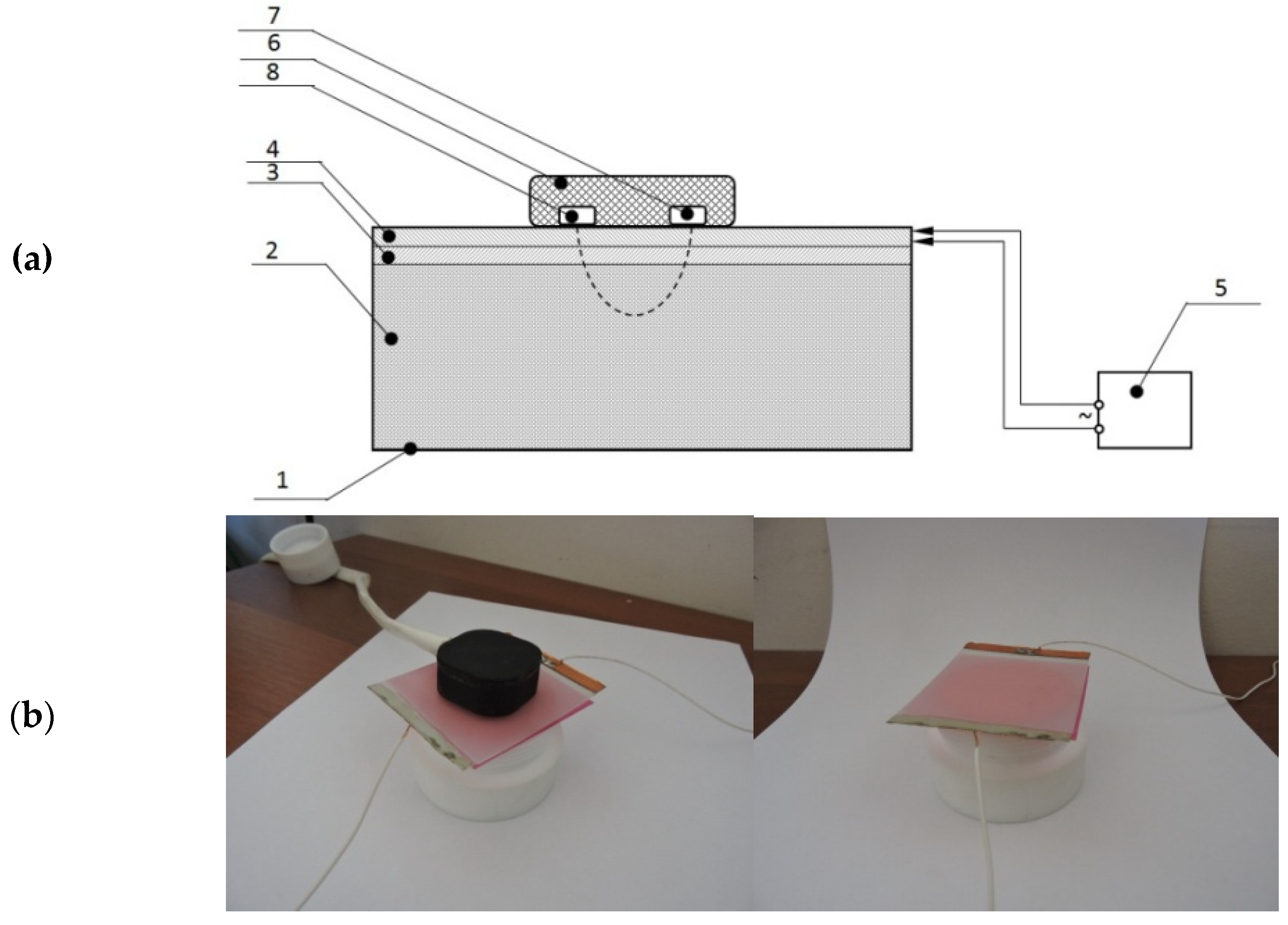
3.2. Peripheral Tissue Probe Design
3.3. Cerebral Optical Probe Design
4. Base Metrological Equipment
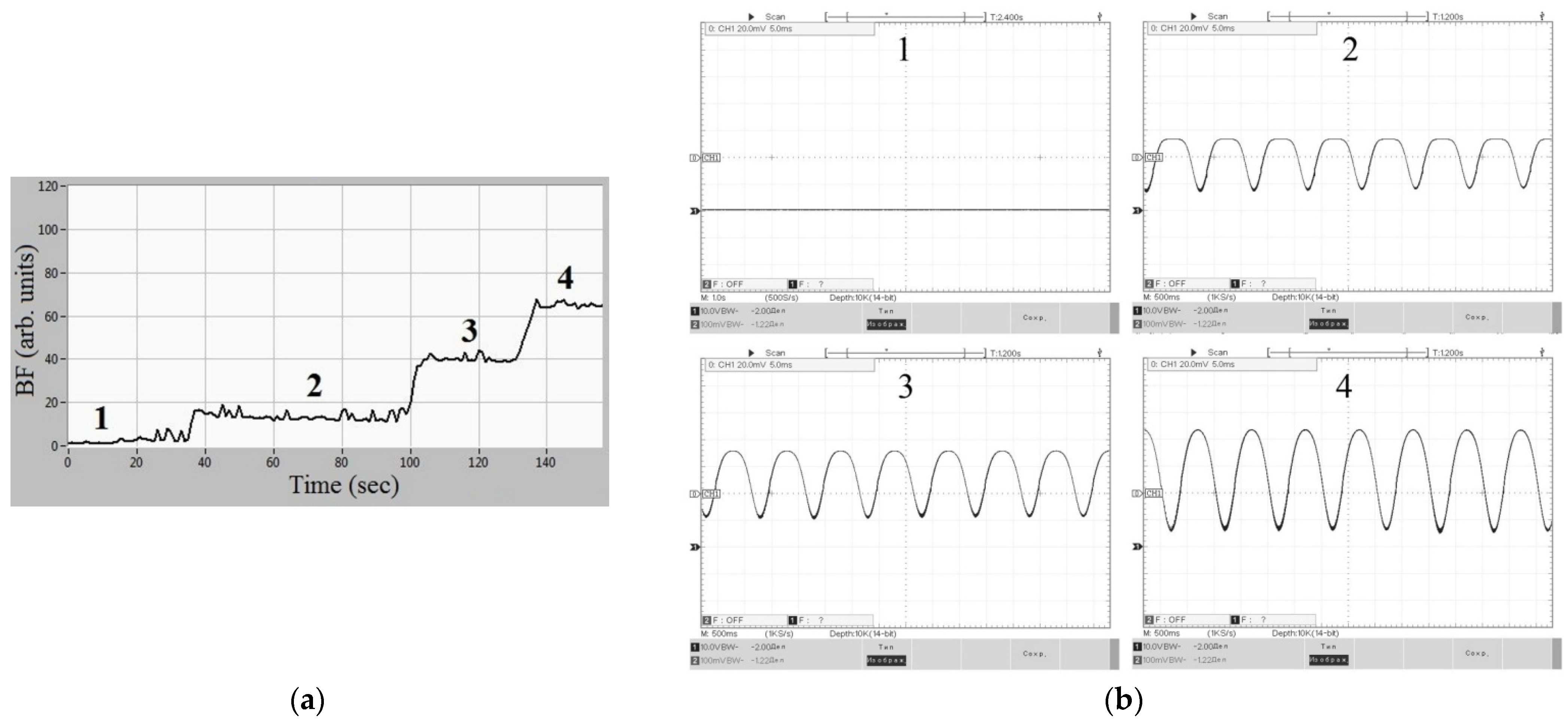
4.1. Imitation Measure for the IOFF Technique
4.2. Imitation Measure for the Cerebral Optical Probe
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nitzan, M.; Romem, A.; Koppel, R. Pulse oximetry: Fundamentals and technology update. Med. Devices 2014, 7, 231–239. [Google Scholar] [CrossRef]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1–R39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lange, F.; Tachtsidis, I. Clinical brain monitoring with time domain NIRS: A review and future perspectives. Appl. Sci. 2019, 9, 1612. [Google Scholar] [CrossRef] [Green Version]
- Fredriksson, I.; Fors, C.; Johansson, J. Laser Doppler Flowmetry—A Theoretical Framework. Department of Biomedical Engineering, Linköping University. 2007. Available online: https://www.researchgate.net/publication/238678169 (accessed on 18 March 2022).
- Drexler, W.; Liu, M.; Kumar, A.; Kamali, T.; Unterhuber, A.; Leitgeb, R.A. Optical coherence tomography today: Speed, contrast, and multimodality. J. Biomed. Opt. 2014, 19, 071412. [Google Scholar] [CrossRef] [PubMed]
- Yu, G. Diffuse correlation spectroscopy (DCS): A diagnostic tool for assessing tissue blood flow in vascular-related diseases and therapies. Curr. Med. Imaging 2012, 8, 194–210. [Google Scholar] [CrossRef]
- Rogatkin, D.A.; Dunaev, A.V.; Lapaeva, L.G. Metrological providing for methods and devices of non-invasive medical spectrophotometry. Biomed. Eng. 2010, 44, 66–77. [Google Scholar] [CrossRef]
- ISO 80601-2-61:2017. Medical Electrical Equipment—Part 2-61: Particular Requirements for the Basic Safety and Essential Performance of Pulse Oximeter Equipment. 2017. Available online: https://www.iso.org/standard/67963.html (accessed on 18 March 2022).
- Rogatkin, D. Biophotonic devices and technologies in problems of medical diagnostics. Quantum Electron. 2021, 51, 365. [Google Scholar] [CrossRef]
- Binzoni, T.; Martelli, F. Study on the mathematical relationship existing between single-photon laser-Doppler flowmetry and diffuse correlation spectroscopy with static background. J. Opt. Soc. Am. A 2017, 34, 2096–2101. [Google Scholar] [CrossRef]
- Fredriksson, I.; Larsson, M. On the equivalence and differences between laser Doppler flowmetry and laser speckle contrast analysis. J. Biomed. Opt. 2016, 21, 126018. [Google Scholar] [CrossRef]
- ISO 80601-2-85:2021. Medical Electrical Equipment—Part 2-85: Particular Requirements for the Basic Safety and Essential Performance of Cerebral Tissue Oximeter Equipment. 2021. Available online: https://www.iso.org/standard/72442.html (accessed on 18 March 2022).
- Dunaev, A.V.; Zherebtsov, E.A.; Rogatkin, D.A.; Stewart, N.A.; Sokolovski, E.U. Substantiation of medical and technical requirements for noninvasive spectrophotometric diagnostic devices. J. Biomed. Opt. 2013, 18, 107009. [Google Scholar] [CrossRef]
- Afshari, A.; Ghassemi, P.; Lin, J.; Halprin, M.; Wang, J.; Mendoza, G.; Weininger, S.; Pfefer, T.J. Cerebral oximetry performance testing with a 3D-printed vascular array phantom. Biomed. Opt. Exp. 2019, 10, 3731–3746. [Google Scholar] [CrossRef]
- Dunaev, A.V.; Stewart, N.A.; Sokolovski, S.G.; Rafailov, E.U.; Zherebtsov, E.A.; Rogatkin, D.A. Novel measure for the calibration of laser Doppler flowmetry devices. Proc. SPIE 2014, 8936, 89360D. [Google Scholar] [CrossRef] [Green Version]
- Hyttel-Sorensen, S.; Kleiser, S.; Wolf, M.; Greisen, G. Calibration of a prototype NIRS oximeter against two commercial devices on a blood-lipid phantom. Biomed. Opt. Exp. 2013, 4, 1662–1672. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rogatkin, D.A.; Lapaeva, L.G. Prospects for development of noninvasive spectrophotometric medical diagnosis. Biomed. Eng. 2003, 37, 217–222. [Google Scholar] [CrossRef]
- Rogatkin, D.A.; Sokolovski, S.G.; Fedorova, K.A.; Stewart, N.A.; Sidorov, V.V.; Rafailov, E.U. Basic principles of design and functioning of multifunctional laser diagnostic system for non-invasive medical spectrophotometry. Proc. SPIE 2011, 7890, 78901H. [Google Scholar] [CrossRef] [Green Version]
- Rogatkin, D.A.; Lapaeva, L.G.; Petritskaya, E.N.; Sidorov, V.V.; Shumskiy, V.I. Multifunctional laser noninvasive spectroscopic system for medical diagnostics and some metrological provisions for that. Proc. SPIE 2009, 7368, 73681Y. [Google Scholar] [CrossRef]
- Ferreira, M. The role of metrology in the field of medical devices. Int. J. Metrol. Qual. Eng. 2011, 2, 135–140. [Google Scholar] [CrossRef] [Green Version]
- Hyttel-Sorensen, S.; Hessel, T.W.; Cour, A.; Greisen, G. A comparison between two NIRS oximeters (INVOS, OxyPrem) using measurement on the arm of adults and head of infants after caesarean section. Biomed. Opt. Exp. 2014, 5, 3671–3683. [Google Scholar] [CrossRef] [Green Version]
- Kleiser, S.; Ostojic, D.; Andresen, B.; Nasseri, N.; Isler, H.; Scholkmann, F.; Karen, T.; Greisen, G.; Wolf, M. Comparison of tissue oximeters on a liquid phantom with adjustable optical properties: An extension. Biomed. Opt. Exp. 2018, 9, 86–101. [Google Scholar] [CrossRef] [Green Version]
- Seong, M.; Phillips, Z.; Mai, P.M.; Yeo, C.; Song, C.; Lee, K.; Kim, J.G. Simultaneous blood flow and blood oxygenation measurements using a combination of diffuse speckle contrast analysis and near-infrared spectroscopy. J. Biomed. Opt. 2016, 21, 027001. [Google Scholar] [CrossRef]
- Moor Instruments. Innovation in Microvascular Assessment. Available online: https://www.moor.co.uk/products (accessed on 28 February 2022).
- Lapitan, D.; Rogatkin, D. Optical incoherent technique for noninvasive assessment of blood flow in tissues: Theoretical model and experimental study. J. Biophotonics 2021, 14, e202000459. [Google Scholar] [CrossRef]
- Davie, S.N.; Grocott, H.P. Impact of extracranial contamination on regional cerebral oxygen saturation: A comparison of three cerebral oximetry technologies. Anesthesiology 2012, 116, 834–840. [Google Scholar] [CrossRef] [Green Version]
- Steppan, J.; Hogue, C.W., Jr. Cerebral and tissue oximetry. Best Pract. Res. Clin. Anaesthesiol. 2014, 28, 429–439. [Google Scholar] [CrossRef] [Green Version]
- Lapitan, D.G.; Tarasov, A.P.; Parnovskaya, A.D. Theoretical justification of sensor parameters for cerebral oximeter based on CT data and Monte Carlo modeling of light transport. In Proceedings of the 2021 Radiation and Scattering of Electromagnetic Waves (RSEMW) International Conference, Divnomorskoe, Russia, 28 June–2 July 2021; pp. 357–360. [Google Scholar] [CrossRef]
- Tarasov, A.P.; Lapitan, D.G.; Parnovskaya, A.D. Sensor for Optical Cerebral Oximeter. R.F. Patent RU 2770266 C2, 16 July 2020. [Google Scholar]
- Budidha, K.; Rybynok, V.; Kyriacou, P.A. Design and development of a modular multichannel photoplethysmography system. IEEE Trans. Instrum. Meas. 2018, 67, 1954–1965. [Google Scholar] [CrossRef] [Green Version]
- Lapitan, D.G.; Raznitsyn, O.A. A method and a device prototype for noninvasive measurements of blood perfusion in a tissue. Instrum. Exp. Tech. 2018, 61, 745–750. [Google Scholar] [CrossRef]
- Lapitan, D.G.; Tarasov, A.P. Analytical assessment of the modulation depth of photoplethysmographic signal based on the modified Beer-Lambert law. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Optoelectronics and Lasers (CAOL), Sozopol, Bulgaria, 6–8 September 2019; pp. 103–106. [Google Scholar] [CrossRef]
- Del Bianco, S.; Martelli, F.; Zaccanti, G. Penetration depth of light re-emitted by a diffusive medium: Theoretical and experimental investigation. Phys. Med. Biol. 2002, 47, 4131–4144. [Google Scholar] [CrossRef]
- Weiss, G.H.; Nossal, R.; Bonner, R.F. Statistics of penetration depth of photons re-emitted from irradiated tissue. J. Mod. Opt. 1989, 36, 349–359. [Google Scholar] [CrossRef]
- Akl, T.J.; Wilson, M.A.; Ericson, M.N.; Coté, G.L. Intestinal perfusion monitoring using photoplethysmography. J. Biomed. Opt. 2013, 18, 087005. [Google Scholar] [CrossRef] [Green Version]
- Meglinski, I.V.; Matcher, S.J. Computer simulation of the skin reflectance spectra. Comput. Methods Programs Biomed. 2003, 70, 179–186. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, S.; Budidha, K.; Kyriacou, P.A. Investigating the origin of photoplethysmography using a multiwavelength Monte Carlo model. Physiol. Meas. 2020, 41, 084001. [Google Scholar] [CrossRef]
- Saidi, I.S. Transcutaneous Optical Measurement of Hyperbilirubinemia in Neonates. Ph.D. Thesis, Rice University, Houston, TX, USA, 1992. [Google Scholar]
- Jacques, S.L. Origins of tissue optical properties in the UVA, visible, and NIR regions. OSA TOPS Adv. Opt. Imaging Phot. Migr. 1996, 2, 364–369. [Google Scholar]
- Bosschaart, N.; Edelman, G.J.; Aalders, M.C.; van Leeuwen, T.G.; Faber, D.J. A literature review and novel theoretical approach on the optical properties of whole blood. Lasers Med. Sci. 2014, 29, 453–479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hale, G.M.; Querry, M.R. Optical constants of water in the 200-nm to 200-m wavelength region. Appl. Opt. 1973, 2, 555. [Google Scholar] [CrossRef]
- Meglinski, I.V.; Matcher, S.J. Quantitative assessment of skin layers absorption and skin reflectance spectra simulation in the visible and near-infrared spectral regions. Physiol. Meas. 2002, 23, 741–753. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef]
- Reuss, J.L.; Siker, D. The pulse in reflectance pulse oximetry: Modeling and experimental studies. J. Clin. Monit. Comput. 2004, 18, 289–299. [Google Scholar] [CrossRef]
- Prahl, S. Optical Absorption of Hemoglobin. 1999. Available online: https://omlc.org/spectra/hemoglobin (accessed on 18 March 2022).
- Biswas, T.K.; Luu, T.M. In vivo MR measurement of refractive index, relative water content and T2 relaxation time of various brain lesions with clinical application to discriminate brain lesions. Internet J. Radiol. 2011, 13, 1–9. [Google Scholar]
- Yaroslavsky, A.N.; Schulze, P.C.; Yaroslavsky, I.V.; Schober, R.; Ulrich, F.; Schwarzmaier, H.J. Optical properties of selected native and coagulated human brain tissues in vitro in the visible and near infrared spectral range. Phys. Med. Biol. 2002, 47, 2059. [Google Scholar] [CrossRef]
- Okada, E.; Delpy, D.T. Near-infrared light propagation in an adult head model. II. Effect of superficial tissue thickness on the sensitivity of the near-infrared spectroscopy signal. Appl. Opt. 2003, 42, 2915–2921. [Google Scholar] [CrossRef] [Green Version]
- Ding, H.; Lu, J.Q.; Wooden, W.A.; Kragel, P.J.; Hu, X.H. Refractive indices of human skin tissues at eight wavelengths and estimated dispersion relations between 300 and 1600 nm. Phys. Med. Biol. 2006, 51, 1479. [Google Scholar] [CrossRef] [Green Version]
- Bashkatov, A.N.; Genina, E.A.; Tuchin, V.V. Optical properties of skin, subcutaneous, and muscle tissues: A review. J. Innov. Opt. Health Sci. 2011, 4, 9–38. [Google Scholar] [CrossRef]
- Stritzel, J.; Rahlves, M.; Roth, B. Refractive-index measurement and inverse correction using optical coherence tomography. Opt. Lett. 2015, 40, 5558–5561. [Google Scholar] [CrossRef]
- Genina, E.A.; Bashkatov, A.N.; Tuchin, V.V. Optical clearing of cranial bone. Adv. Opt. Technol. 2008, 2008, 267867. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, A.P.; Vishnyakova, M.V., Jr.; Ivlieva, A.L.; Davydov, D.V.; Podrez, D.V.; Rogatkin, D.A.; Vishnyakova, M.V. A technique of multidetector computed tomography for optical cerebral oximetry. Alm. Clin. Med. 2015, 43, 52–57. (In Russian) [Google Scholar]
- Haeussinger, F.B.; Heinzel, S.; Hahn, T.; Schecklmann, M.; Ehlis, A.C.; Fallgatter, A.J. Simulation of near-infrared light absorption considering individual head and prefrontal cortex anatomy: Implications for optical neuroimaging. PLoS ONE 2011, 6, e26377. [Google Scholar] [CrossRef]
- Li, T.; Gong, H.; Luo, Q. Visualization of light propagation in visible Chinese human head for functional near-infrared spectroscopy. J. Biomed. Opt. 2011, 16, 045001. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Meth. Programs Biomed. 1995, 47, 131. [Google Scholar] [CrossRef]
- Tarasov, A.P. Acceleration of Monte Carlo simulation of light transport in tissues using disk-detector geometry in the backscattering problem. In Proceedings of the 2020 International Conference Laser Optics (ICLO), Saint Petersburg, Russia, 2–6 November 2020; p. 1. [Google Scholar] [CrossRef]
- Okada, E.; Firbank, M.; Schweiger, M.; Arridge, S.R.; Cope, M.; Delpy, D.T. Theoretical and experimental investigation of near-infrared light propagation in a model of the adult head. Appl. Opt. 1997, 36, 21–31. [Google Scholar] [CrossRef]
- Rogatkin, D.A.; Lapaeva, L.G.; Bychenkov, O.A.; Tereshchenko, S.G.; Shumskii, V.I. Principal sources of errors in noninvasive medical spectrophotometry. Part 1. Physicotechnical sources and factors of errors. Meas. Tech. 2013, 56, 201–210. [Google Scholar] [CrossRef]
- Fredriksson, I.; Larsson, M.; Salomonsson, F.; Stromberg, T. Improved calibration procedure for laser Doppler perfusion monitors. Proc. SPIE 2011, 7906, 790602. [Google Scholar] [CrossRef] [Green Version]







| Chromophore | Optical Parameter | Wavelength, nm | |||||
|---|---|---|---|---|---|---|---|
| 470 | 525 | 568 | 660 | 805 | 940 | ||
| Blood | , cm−1 (StO2 = 75%, Hct = 45%) | 148.6 | 162.1 | 229.4 | 5.23 | 4.08 | 5.95 |
| Water | , cm−1 | 0.000247 | 0.00032 | 0.00079 | 0.0032 | 0.267 | 0.36 |
| Skin | , cm−1 = 0.5) | 15.49 | 16.65 | 23.28 | 0.73 | 0.65 | 0.84 |
| , cm−1 | 54.8 | 43.6 | 37.7 | 29.8 | 23.2 | 19.8 | |
| Tissue Type | Thickness (cm) | ||||
|---|---|---|---|---|---|
| Scalp | 0.43, 0.3 | 196, 178 | 0.9 | 1.38 | 0.44 |
| Skull | 0.15, 0.22 | 160, 150 | 0.9 | 1.52 | 0.63 |
| CSF | 0.04 | 24 | 0.9 | 1.33 | 0.3 |
| Grey matter | 0.25, 0.35 | 80, 65 | 0.9 | 1.40 | 0.4 |
| White matter | 0.9, 1 | 350, 330 | 0.9 | 1.41 | ∞ |
| Optical Parameter | Wavelength, nm | ||
|---|---|---|---|
| 660 | 810 | 940 | |
| , cm−1 | 0.040 | 0.022 | 0.015 |
| , cm−1 | 280 | 120 | 70 |
| g | 0.81 | 0.91 | 0.94 |
| Rd,% | 92 | 88 | 83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarasov, A.; Lapitan, D.; Rogatkin, D. Combined Non-Invasive Optical Oximeter and Flowmeter with Basic Metrological Equipment. Photonics 2022, 9, 392. https://doi.org/10.3390/photonics9060392
Tarasov A, Lapitan D, Rogatkin D. Combined Non-Invasive Optical Oximeter and Flowmeter with Basic Metrological Equipment. Photonics. 2022; 9(6):392. https://doi.org/10.3390/photonics9060392
Chicago/Turabian StyleTarasov, Andrey, Denis Lapitan, and Dmitry Rogatkin. 2022. "Combined Non-Invasive Optical Oximeter and Flowmeter with Basic Metrological Equipment" Photonics 9, no. 6: 392. https://doi.org/10.3390/photonics9060392
APA StyleTarasov, A., Lapitan, D., & Rogatkin, D. (2022). Combined Non-Invasive Optical Oximeter and Flowmeter with Basic Metrological Equipment. Photonics, 9(6), 392. https://doi.org/10.3390/photonics9060392





