Multiplexed Holographic Combiner with Extended Eye Box Fabricated by Wave Front Printing
Abstract
1. Introduction
2. Materials and Methods
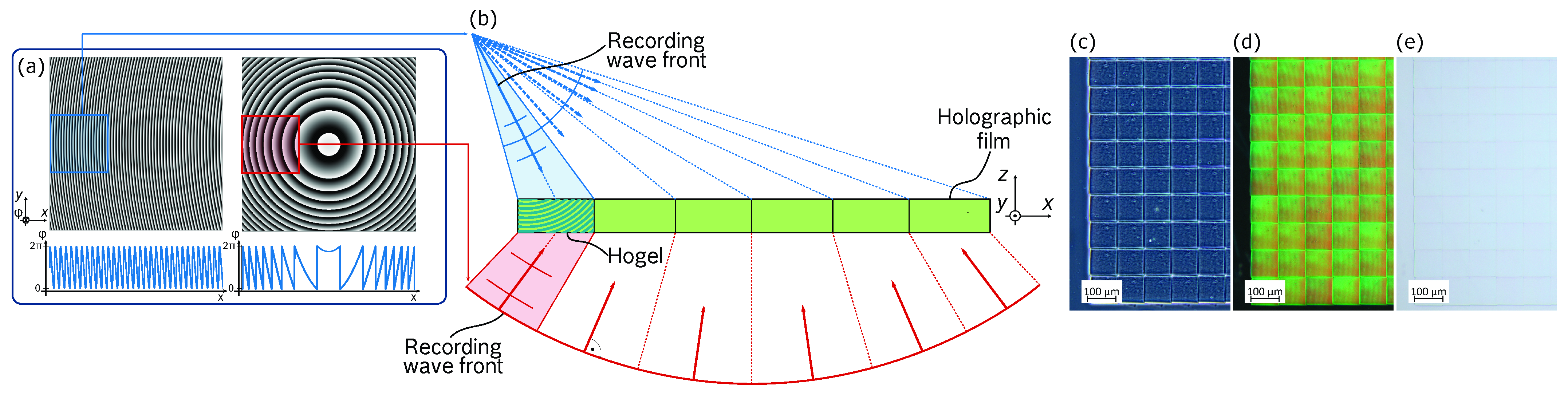
2.1. Phase Pattern Generation
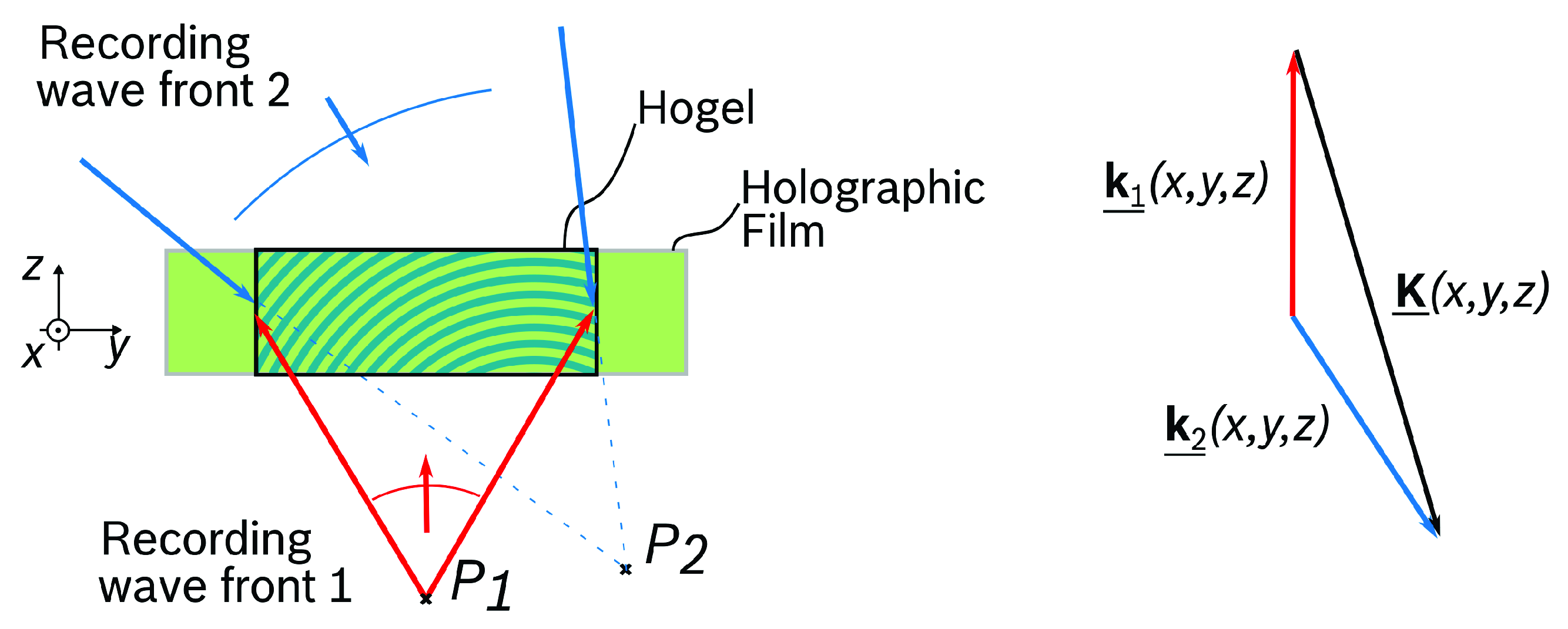
2.2. Wave Front Recording Setup
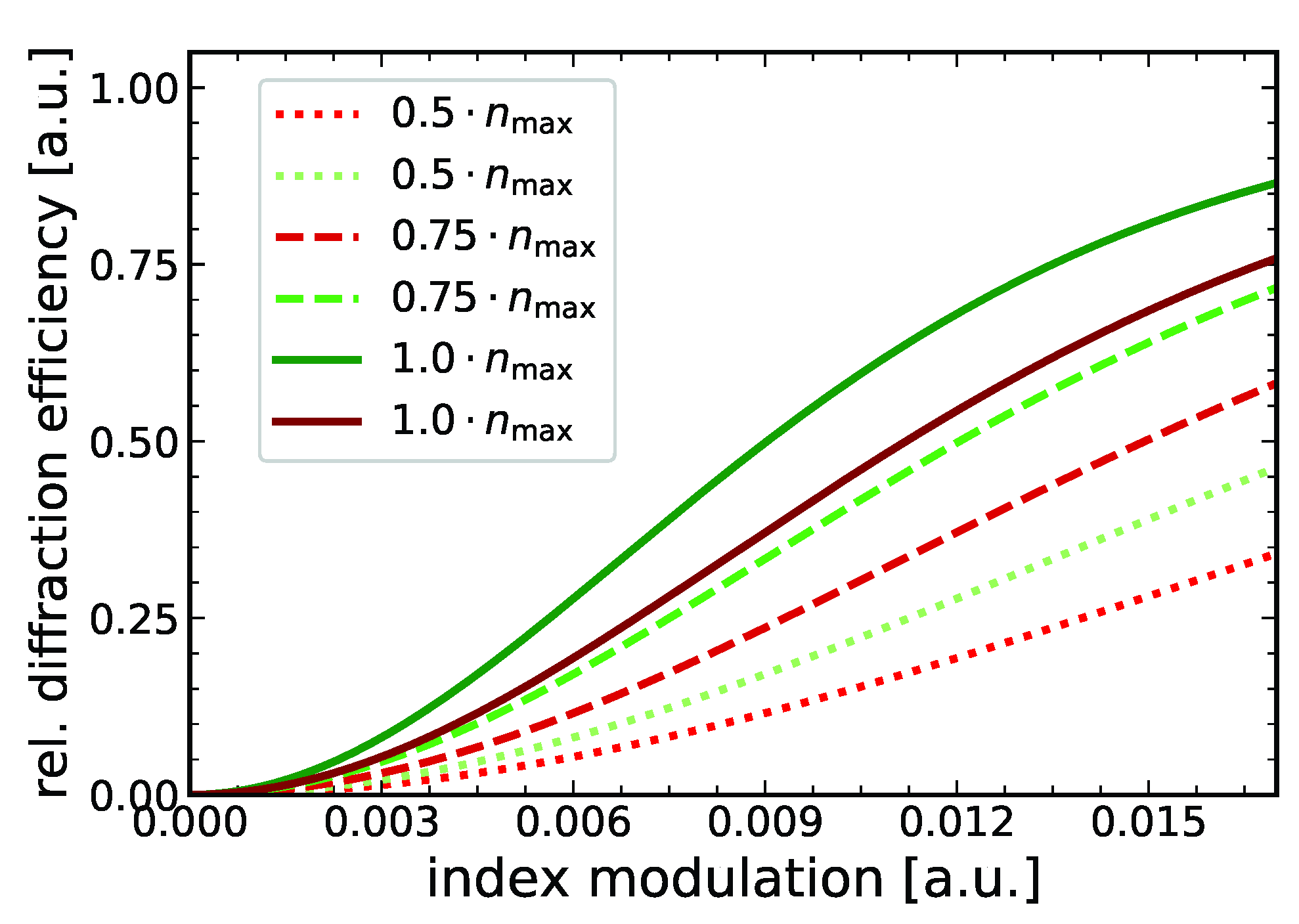
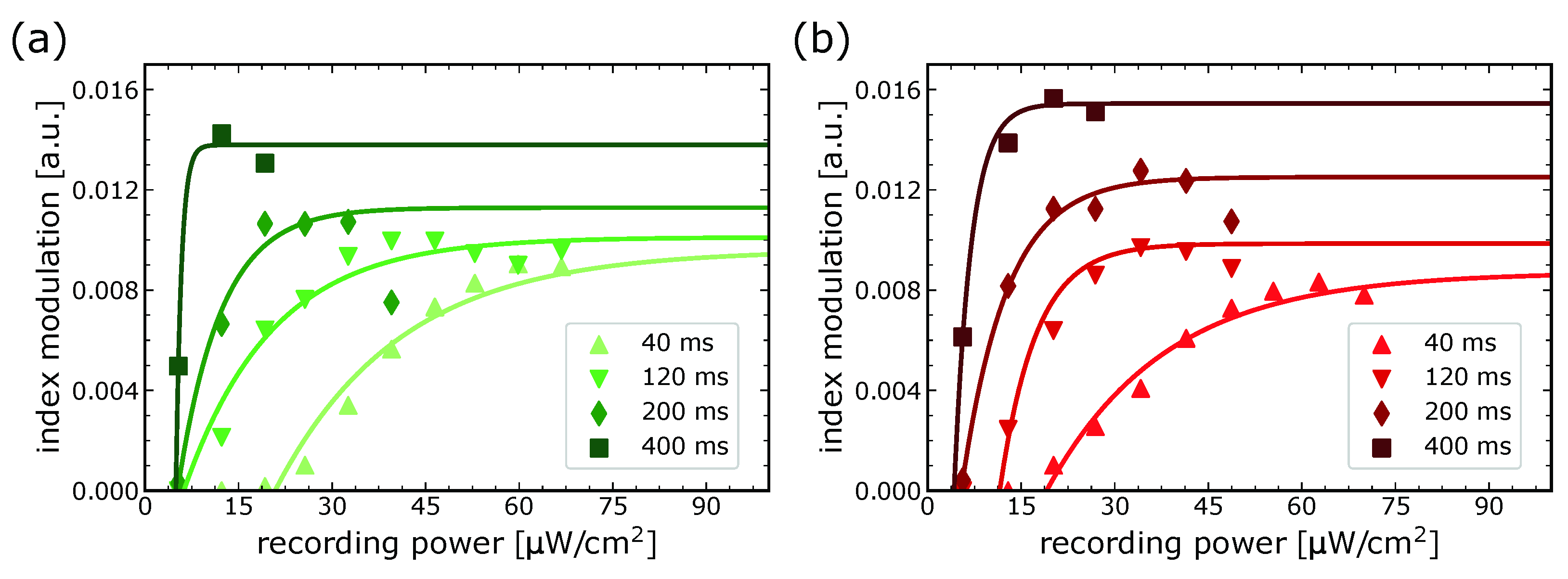
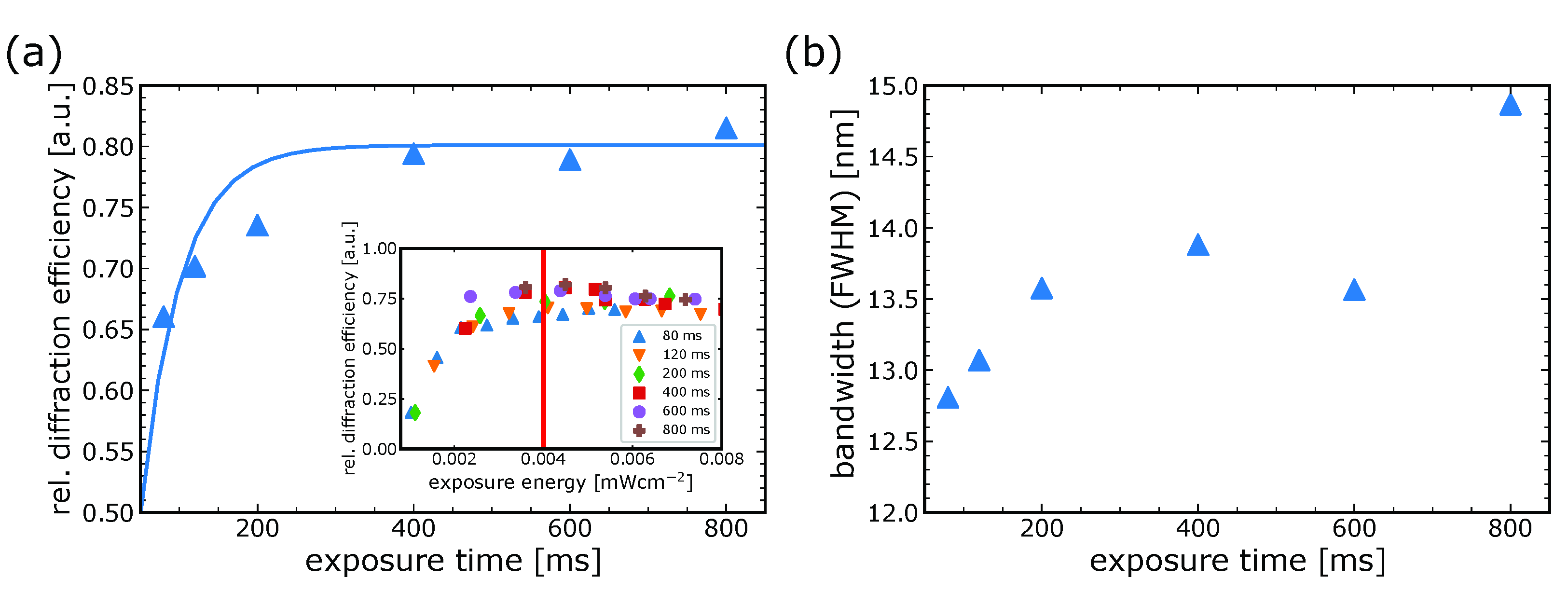
2.3. Recording Parameters Determination
3. Results and Discussion
3.1. Monochromatic Recording Parameters
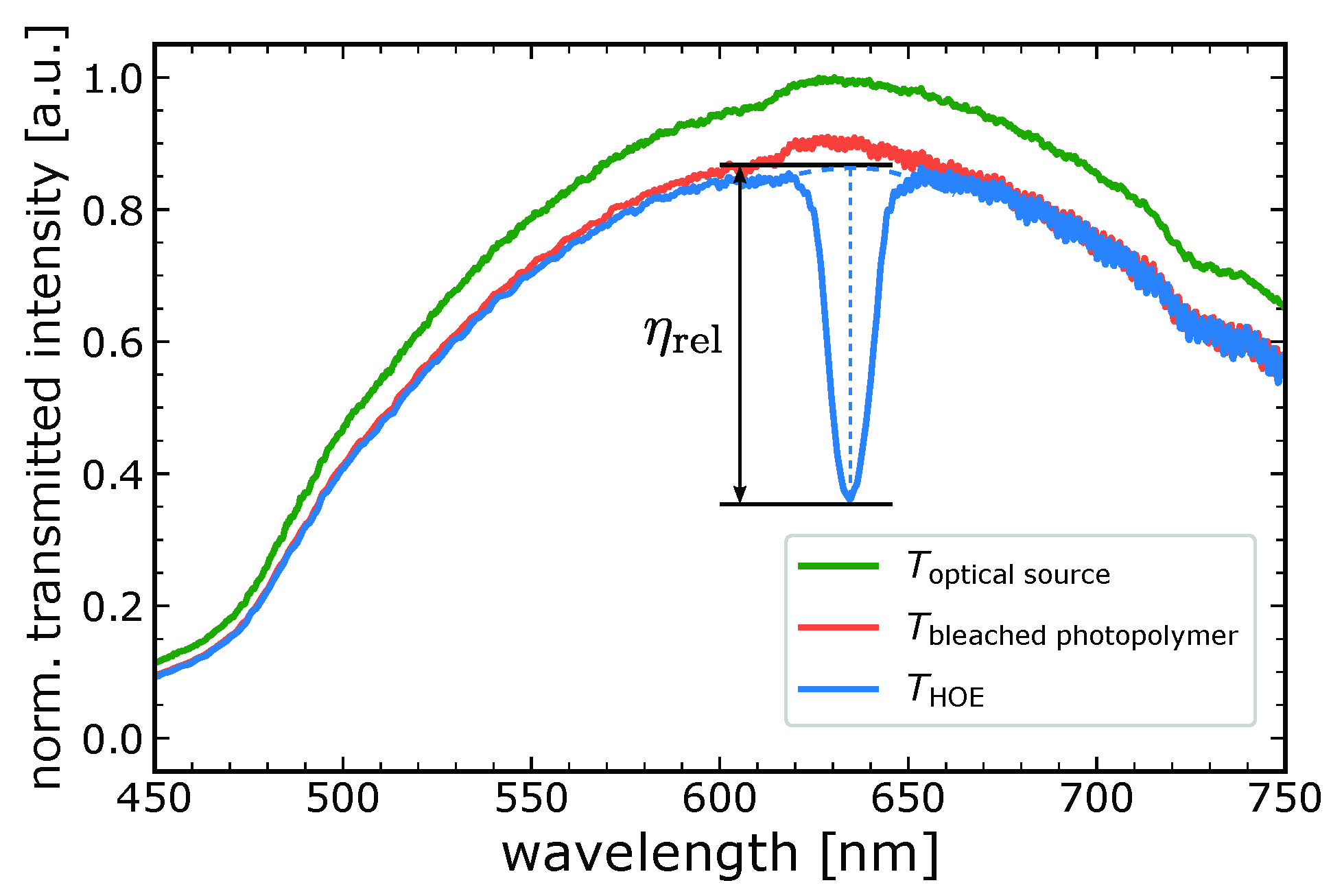
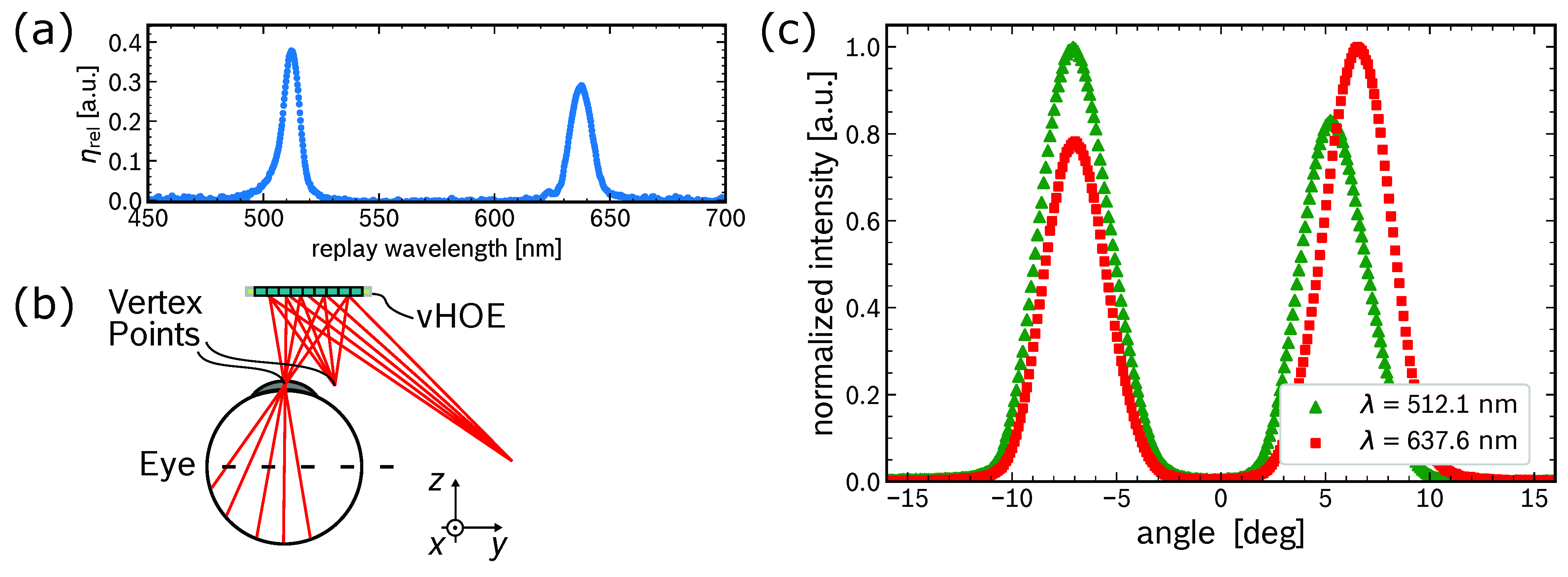
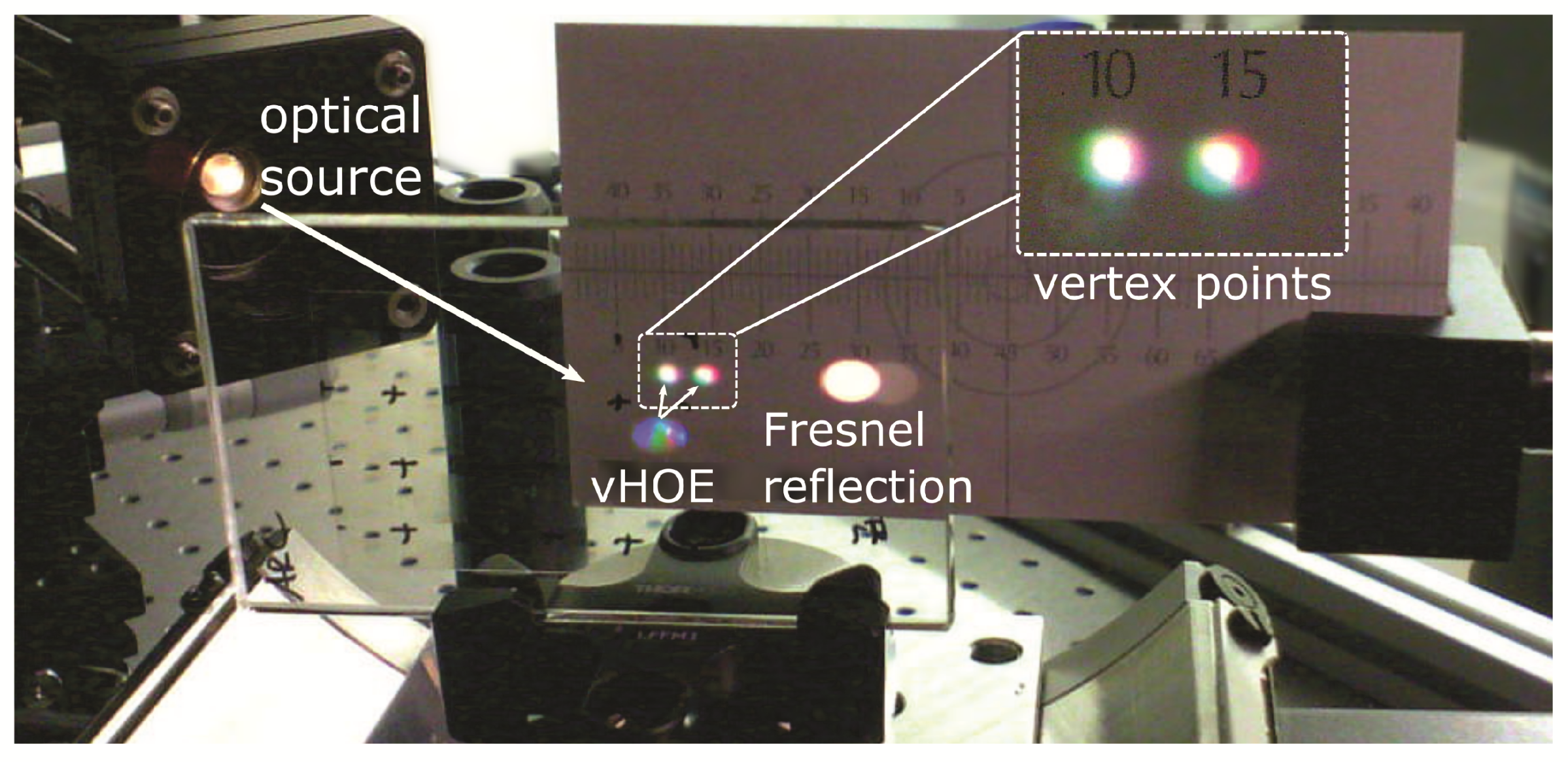
3.2. Spectral Multiplexing
3.3. Angular Multiplexing
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tezer, M.; Yildiz, E.P.; Masalimova, A.R.R.; Fatkhutdinova, A.M.; Zheltukhina, M.R.R.; Khairullina, E.R. Trends of Augmented Reality Applications and Research throughout the World: Meta-Analysis of Theses, Articles and Papers between 2001-2019 Years. Int. J. Emerg. Technol. Learn. IJET 2019, 14, 154–174. [Google Scholar] [CrossRef]
- Rabbi, I.; Ullah, S. A Survey on Augmented Reality Challenges and Tracking. Acta Graph. 2013, 24, 29–46. [Google Scholar]
- Carmigniani, J.; Furht, B.; Anisetti, M.; Ceravolo, P.; Damiani, E.; Ivkovic, M. Augmented reality technologies, systems and applications. Multimed. Tools Appl. 2011, 51, 341–377. [Google Scholar] [CrossRef]
- Brooker, G. Modern Classical Optics; Oxford Master Series in Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Kim, S.B.; Park, J.H. Optical see-through Maxwellian near-to-eye display with an enlarged eyebox. Opt. Lett. 2018, 43, 767–770. [Google Scholar] [CrossRef]
- Lin, T.; Zhan, T.; Zou, J.; Fan, F.; Wu, S.T. Maxwellian near-eye display with an expanded eyebox. Opt. Express 2020, 28, 38616–38625. [Google Scholar] [CrossRef]
- Jang, C.; Bang, K.; Li, G.; Lee, B. Holographic Near-Eye Display with Expanded Eye-Box. ACM Trans. Graph. 2018, 37, 1–14. [Google Scholar] [CrossRef]
- Hedili, M.K.; Soner, B.; Ulusoy, E.; Urey, H. Light-efficient augmented reality display with steerable eyebox. Opt. Express 2019, 27, 12572–12581. [Google Scholar] [CrossRef]
- Park, J.H.; Kim, S.B. Optical see-through holographic near-eye-display with eyebox steering and depth of field control. Opt. Express 2018, 26, 27076–27088. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, Y.; Stengel, M.; Akşit, K.; Albert, R.; Boudaoud, B.; Greer, T.; Kim, J.; Lopes, W.; Majercik, Z.; et al. Foveated AR: Dynamically-Foveated Augmented Reality Display. ACM Trans. Graph. 2019, 38, 1–15. [Google Scholar] [CrossRef]
- Kim, N.; Piao, Y.L.; Wu, H.Y. Holographic optical elements and application. In Holographic Materials and Optical Systems; IntechOpen: Rijeka, Croatia, 2017; Chapter 5; pp. 3–25. [Google Scholar]
- Sabel, T.; Lensen, M.C. Volume holography: Novel materials, methods and applications. In Holographic Materials and Optical Systems; IntechOpen: Rijeka, Croatia, 2017; Chapter 1; pp. 3–25. [Google Scholar]
- Martin, S.; Akbari, H.; Keshri, S.; Bade, D.; Naydenova, I.; Murphy, K.; Toal, V. Holographically recorded low spatial frequency volume Bragg gratings and holographic optical elements. In Holographic Materials and Optical Systems; IntechOpen: Rijeka, Croatia, 2017; Chapter 4; pp. 73–98. [Google Scholar]
- Hofmann, J.; Fiess, R.; Kick, M.; Stork, W. Extended holographic wave front printer setup employing two spatial light modulators. Proc. SPIE 2019, 11030. [Google Scholar] [CrossRef]
- Jang, C.; Mercier, O.; Bang, K.; Li, G.; Zhao, Y.; Lanman, D. Design and Fabrication of Freeform Holographic Optical Elements. ACM Trans. Graph. 2020, 39. [Google Scholar] [CrossRef]
- Yatagai, T.; Camacho-Basilio, J.G.; Onda, H. Recording of computer generated holograms on an optical disk master. Appl. Opt. 1989, 28, 1042. [Google Scholar] [CrossRef] [PubMed]
- Cable, A. Production of computer-generated holograms on recordable compact disk media using a compact disk writer. Opt. Eng. 2003, 42, 2514. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Morishima, M.; Usui, A. Computer-generated holograms on a CD-R disk. Proc. SPIE 2004, 5290, 42–49. [Google Scholar] [CrossRef]
- Matsushima, K.; Kobayashi, S.; Miyauchi, H. A high-resolution fringe printer for studying synthetic holograms. Proc. SPIE 2006, 6136, 347–354. [Google Scholar] [CrossRef]
- Kang, H.; Stoykova, E.; Kim, Y.; Hong, S.; Park, J.; Hong, J. Color wavefront printer with mosaic delivery of primary colors. Opt. Commun. 2015, 350, 47–55. [Google Scholar] [CrossRef]
- Miyamoto, O.; Yamaguchi, T.; Yoshikawa, H. The volume hologram printer to record the wavefront of a 3D object. Proc. SPIE 2012, 8281, 153–162. [Google Scholar] [CrossRef]
- Nishii, W.; Matsushima, K. A wavefront printer using phase-only spatial light modulator for producing computer-generated volume holograms. Proc. SPIE 2014, 9006, 323–330. [Google Scholar] [CrossRef]
- Ramsbottom, A.P.; Sergeant, S.A.; Sheel, D.W. Holography for automotive head-up displays. Proc. SPIE 1992, 1667, 146–164. [Google Scholar] [CrossRef]
- Ando, T.; Yamasaki, K.; Okamoto, M.; Matsumoto, T.; Shimizu, E. Retinal projection display using holographic optical element. Proc. SPIE 2000, 3956, 211–216. [Google Scholar] [CrossRef]
- Takahashi, H.; Hirooka, S. Stereoscopic see-through retinal projection head-mounted display. Proc. SPIE 2008, 6803, 559–566. [Google Scholar] [CrossRef]
- Kick, M. Assembly of a Holographic Wave Front Printer for Realization of Novel Optical Systems. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2018. [Google Scholar]
- Hofmann, J.; Fiess, R.; Stork, W. Holographic wave front printing for fabrication of reflection holograms with arbitrary recording wave fronts. Proc. SPIE 2020, 11306, 1–7. [Google Scholar] [CrossRef]
- Wilm, T.; Höckh, S.; Fiess, R.; Stork, W. Holographic combiners for augmented reality applications fabricated by wave front recording. Proc. SPIE 2021, 11815, 13–22. [Google Scholar] [CrossRef]
- Noll, R.J. Zernike polynomials and atmospheric turbulence. J. Opt. Soc. Am. 1976, 66, 207–211. [Google Scholar] [CrossRef]
- Bruder, F.; Fäcke, T.; Rölle, T. The Chemistry and Physics of Bayfol® HX Film Holographic Photopolymer. Polymers 2017, 9, 472. [Google Scholar] [CrossRef] [PubMed]
- Brotherton-Ratcliffe, D. Understanding Diffraction in Volume Gratings and Holograms. In Holography; IntechOpen: Rijeka, Croatia, 2013; Chapter 1. [Google Scholar] [CrossRef][Green Version]
- Kogelnik, H. Coupled Wave Theory for Thick Hologram Gratings. Bell Syst. Tech. J. 1969, 48, 2909–2947. [Google Scholar] [CrossRef]
- Brotherton-Ratcliffe, D. Analytical treatment of the polychromatic spatially multiplexed volume holographic grating. Appl. Opt. 2012, 51, 7188–7199. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Martín, I.; Marín-Sáez, J.; Gómez-Climente, M.; Chemisana, D.; Collados, M.V.; Atencia, J. Full-color multiplexed reflection hologram of diffusing objects recorded by using simultaneous exposure with different times in photopolymer Bayfol® HX. Opt. Laser Technol. 2021, 143, 107303. [Google Scholar] [CrossRef]



| = 515 nm | = 639 nm | |||||
|---|---|---|---|---|---|---|
| t [ms] | [a.u.] | [µJcm] | [a.u.] | [a.u.] | [µJcm] | [a.u.] |
| 40 | 0.0096 | 0.83 | 50.3 | 0.0088 | 0.76 | 52.7 |
| 120 | 0.0101 | 0.75 | 71.1 | 0.0986 | 1.39 | 171.5 |
| 200 | 0.0113 | 1.04 | 143.8 | 0.0125 | 1.08 | 138.0 |
| 400 | 0.0138 | 1.69 | 1156 | 0.0154 | 1.69 | 364.9 |
| = 515 nm | = 639 nm | |
|---|---|---|
| [] | 14.0 | 13.1 |
| [ms] | 389.5 | 263.2 |
| [%] | 39.3 | 41.6 |
| [%] | 37.5 | 38.6 |
| [%] | 39 | 41 |
| = 515 nm | = 639 nm | |
|---|---|---|
| [] | 2.36 × 107 | 1.90 × 107 |
| [] | 2.37 × 107 | 1.89 × 107 |
| [] | 265.9 | 330.4 |
| [] | 264.9 | 331.0 |
| [deg] | 14.6 | 14.6 |
| [deg] | 12.9 | 12.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilm, T.; Kibgies, J.; Fiess, R.; Stork, W. Multiplexed Holographic Combiner with Extended Eye Box Fabricated by Wave Front Printing. Photonics 2022, 9, 419. https://doi.org/10.3390/photonics9060419
Wilm T, Kibgies J, Fiess R, Stork W. Multiplexed Holographic Combiner with Extended Eye Box Fabricated by Wave Front Printing. Photonics. 2022; 9(6):419. https://doi.org/10.3390/photonics9060419
Chicago/Turabian StyleWilm, Tobias, Jens Kibgies, Reinhold Fiess, and Wilhelm Stork. 2022. "Multiplexed Holographic Combiner with Extended Eye Box Fabricated by Wave Front Printing" Photonics 9, no. 6: 419. https://doi.org/10.3390/photonics9060419
APA StyleWilm, T., Kibgies, J., Fiess, R., & Stork, W. (2022). Multiplexed Holographic Combiner with Extended Eye Box Fabricated by Wave Front Printing. Photonics, 9(6), 419. https://doi.org/10.3390/photonics9060419




