1. Introduction
Ultra-intense femtosecond laser pulses can generate extremely physical conditions for the exploration of the frontiers of basic physics and help reveal new phenomena of matter. Consequently, it has attracted widespread attention in recent years [
1,
2,
3,
4]. Since the chirped pulse amplification (CPA) method was proposed in 1985 [
5], more than 50 lasers worldwide have achieved peak powers of several hundred terawatts (TWs) and even petawatts (PWs) [
6,
7,
8]. Several hundred PW femtosecond (PW-fs) laser systems are being developed or built in Europe (ELI-200PW [
9]), Russia (XCLES-200PW [
10]), the USA (OPAL-75PW [
11]), and China (SEL-100PW [
12]). In a femtosecond PW (fs-PW) laser system, the laser pulse is first stretched from femtosecond to nanosecond and subsequently amplified using CPA or optical parametric chirped pulse amplification (OPCPA) [
13] techniques, wherein the chirped nanosecond pulse is compressed to an ultrashort femtosecond pulse using a grating-based pulse compressor in the final stage.
In an fs-PW laser system, the compression system is usually a Treacy four-grating compressor [
14], wherein the first grating surface bears the largest input pulse energy, and the fourth grating surface bears the shortest pulse duration or the highest peak power. Thus, the damage thresholds of the first and fourth gratings limit the maximum input and output pulse energy, respectively. The output laser beam of the main amplifier typically has a large laser spatial intensity modulation (LSIM) owing to the pump laser, and hotspots appear in the beam due to wavefront distortion at high spatial frequency, resulting from the diffuse reflection of dust or defects in optical components. These strong LSIM or hot spots reach the damage threshold of the grating ahead of the average intensity and limits the output pulse energy at the end of the laser system.
Recently, a novel optical design called a multistep pulse compressor (MPC) was proposed to increase the input/output pulse energy of grating-based pulse compressors [
15]. With the MPC method, beam smoothing based on prism pairs is an important process that is used as the pre-compressor step. However, the beam-smoothing process has not yet been thoroughly investigated. Because the prism pair introduces spectral dispersion to the laser pulse with a relative broadband spectrum, this study analyzes the spatial properties in conjunction with the spectral dispersion. The simulation results demonstrated that beam smoothing based on prism pairs can be used to reduce the laser spatial intensity modulation ratio (LSIMR) of the laser beam on the surfaces of the first and last gratings in the compressor. Thus, the pulse energies of the incident and output laser beams can be increased without damaging the grating. Additionally, this beam-smoothing-based prism pair can be applied before the main amplifier to smooth the incident laser beam before the large crystal for high-energy amplification to protect the expensive crystal.
2. Principle of Prism-Pair-Induced Spatial and Spectral Dispersions
A prism pair is a set of commonly used optical dispersion elements that has the advantages of simple composition, flexible operation, low loss, and precisely adjustable spectral dispersion. Negative spectral dispersion is typically induced by prism pairs to compensate for the positive dispersion and achieve ultrashort laser pulses for small laser beams in oscillators. Contrary to the induced useful negative spectral dispersion, the induced spatial dispersion is harmful in many applications. Then, the laser beam passes through the prism pair twice—forward and backward—to automatically compensate for the prism-pair-induced spatial dispersion.
Recently, it was found that the induced spatial dispersion is also useful in laser microscopy and laser micromachining applications [
16,
17]. In these applications, the laser beam is intentionally introduced to an amount of spatial dispersion using a grating/prism pair and then focused using a lens or other optical equipment. The purpose of this special optical design is to achieve the highest focal intensity at the focal point only, so as to ensure that the laser intensity near the focal point decreases rapidly. Thus, the optical section capability will be improved near the focal point, resulting in increased resolution and contrast in microscopy or micromachining applications. This method was named spatiotemporal focusing [
18,
19].
Recently, it was reported that this spatiotemporal focusing can be used in ultrahigh-peak-power laser systems with large beam sizes [
20,
21,
22,
23]. In this MPC optical design, the intentionally induced spatial dispersion using a grating or prism pair was used to smoothen the laser beam with large beam sizes to reduce its LSIMR [
15].
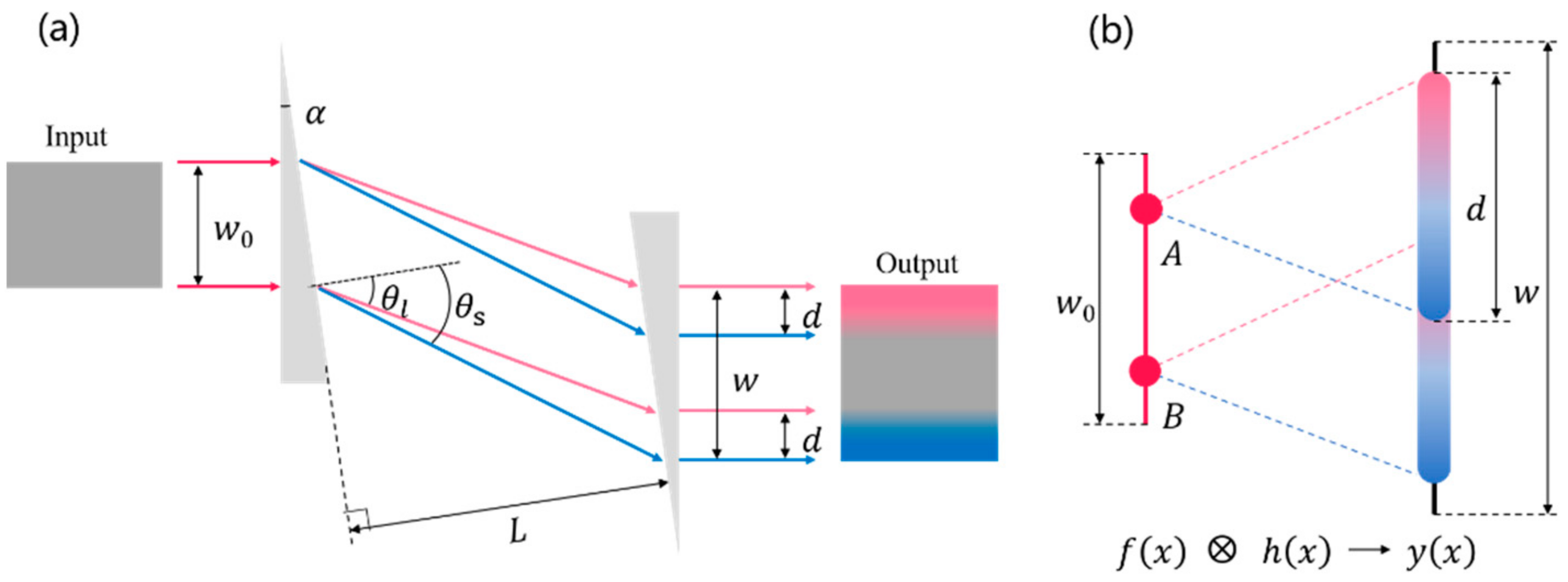
In the spatial domain, the passing of a laser beam through a prism introduces angular dispersion, which extends the laser beam in the angular dispersion direction owing to the broad spectrum, and another prism with the same optical parameters is located parallel to the first one to collimate the output laser beam. The optical setup of the prism pair with two right-angle prisms for laser beam smoothing is shown in
Figure 1a, where
is the perpendicular distance between the two prisms,
is the apex angle of the two prisms,
and
are the exit angles of the shortest and longest wavelengths, respectively,
is the induced spatial dispersion width,
and
are the input and output laser beam widths along the X-axis, respectively. The induced spatial dispersion width
can be expressed as
. Considering the relationship between the exit angle of the beam
and the apex angle of the prism, as well as that between
and the refractive index of the prism pair at different wavelengths, the induced spatial dispersion width
can also be expressed as follows:
where
is the incident angle of the laser beam, and
and
are the refractive indices of the prism pair at the shortest and longest wavelengths, respectively.
and
are the dependent variables related to the incident angle and wavelength. According to the above formulas, the induced spatial dispersion width
is only related to the perpendicular distance between the two prisms
and the prism apex angle
when the wavelength range and the incident angle are constant.
From these equations, it is clear that is linearly related to the distance between the two prisms, and also related to both the apex angle of the prism and the exit angles of the beam . The refractive index of the prism pair is constant at the same wavelength; thus, the changing of the spectral range significantly affects . When the induced spatial dispersion width is smaller than the laser beam size, the center part of the output laser beam has a full bandwidth spectrum and no spatial dispersion, whereas the laser beam on both sides exhibits spatial dispersion.
Owing to the angular dispersion of the prism pair, light with different wavelengths will be output at different angles from the first prism and will be distributed at different positions after being collimated by the second prism. The spatiospectral distribution of the nearby spots of the incident laser beam will overlap in the output beam; therefore, the intensity of the output laser beam is redistributed.
Figure 1b illustrates this redistribution principle using two nearby input light spots, A and B. Assuming that the laser spectra are the same for all spots in the incident laser beam, both A and B will be extended from a spot to a line with a length
. If the distance between A and B is smaller than
, there is spatial overlapping of different wavelengths in the output laser beam for A and B. The process depicted in
Figure 1b, which induces spatial dispersion by angular dispersion, can also be explained using convolution, as expressed in the following equation:
where
is the incident laser intensity distribution function along the X-axis, the function
is the spectral intensity profile projected on the X-axis, and
is the obtained output smoothed beam profile on the X-axis. It is known that a convolution operator can smooth figures or signals. The final laser beam intensity is obtained by accumulating the intensity of light that arrived at the same spatial position through the prism pair. Consequently, the output laser beam is smoothed owing to convolution and intensity redistribution.
Hotspots are the typical damage risk for high-peak-power lasers owing to their small beam size and local high intensity. Therefore, we assume that points A and B have a diameter of ; as a result, the peak power of the two hot spots is decreased by approximately times. After summing all the corresponding spatio-spectral intensity values at every point on the extended output beam line, the beam smoothing effect of the output laser beam is found to be related to the ratio. This indicates that both increasing and reducing have a significant effect on smoothing the output laser beam. Specifically, inducing a larger spatial dispersion width onto hotspots with a high spatial frequency is easier to smooth.
In a PW laser, the laser pulse is usually chirped to the order of nanoseconds to avoid laser-induced damage to the amplification crystal. Compared with the large spectral dispersion of the input laser beam induced by the stretcher, the induced spectral dispersion was negligible. For tens of femtosecond transform-limited laser pulses with a broadband spectrum, the induced small spectral dispersion is important to achieve good compression of the laser pulse. Based on previous works, the spectral dispersion induced by a single pass of a prism pair can be expressed as follows [
24]:
where
and
are the second-order and the third-order dispersions, respectively;
and
are the second-order and the third-order derivatives of the optical path with respect to wavelength, respectively;
is the wavelength;
is the speed of light. Furthermore, it was found that the combination of a prism pair and a grating pair can help to compensate for the third-order dispersion and help to achieve a shorter compressed pulse duration because the prism pair and the grating pair have the same signs for
and opposite signs for
[
14,
24]. Note that the material dispersion of the prism pair discussed here is relatively larger because of the large beam size induced by the large and thick prism; therefore, the spectral dispersion will be seriously affected by the material dispersion compared with the prism pair used for a small beam size, which is discussed in the following section.
4. Simulation Results in Spectral Dispersion
The laser beam passing through the prism pair not only changes the spatial characteristics of the laser beam but also affects its temporal properties. The spectral dispersion induced by the prism pair of the output laser beam consists of the following two parts: the material dispersion of the prism pair and the negative dispersion caused by the angular dispersion of the prism pair. For the PW laser facility, the laser beam is relatively large, and the prism pair used for beam smoothing also has a large optical size, which implies a relatively thick optical path in the prisms. As a result, the positive dispersion induced by the prism pair material is considerable, which is different from the prism pair with a small size. The positive dispersion caused by the material is expressed as follows:
where
and
are the positive dispersions of the second-order and third-order, respectively.
and
are respectively the second-order and the third-order derivatives of the refractive index to wavelength.
is the distance traveled in the prism pair.
For the negative dispersion from the angular dispersion induced by the prism pair, the second-order dispersion GDD and the third-order dispersion TOD are simulated based on formulas (5) and (6), respectively. In the simulation, the apex angle of the prism is 20°, the center wavelength is 925 nm, and the beam size is 370 × 370 mm
2. The spectral shape of the input beam is set to a 7th-order flat-top super-Gaussian, and the spectral range is 825–1025 nm. The GDD and TOD generated by material dispersion are related to the prism insertion; the first prism insertion is 10 mm, and the second prism insertion is 400 mm in this simulation here. For a single prism pair, the induced GDD and TOD with a center wavelength of 925 nm vary with the prism pair distance.
Figure 7b shows the enlarged part marked by the blue box in
Figure 7a. As can be seen, the total introduced GDD and TOD are both positive values at the beginning because the relatively large prism and thick material induce positive dispersion. When the prism pair is spaced by approximately 0.9 m, the angular dispersion induces negative dispersion, and the material-induced positive dispersion is balanced, which induces a nearly zero GDD and TOD. In this case, the induced spatial dispersion width
is approximately 1.3 mm. As the prism pair distance increases, GDD and TOD become negative and increase linearly.
In fact, the loss of the prism pair is low, and thus its absorption can be ignored. The positive and negative values of the second-order and third-order dispersions can be precisely adjusted by adjusting the prism insertion. In other words, the total dispersion of a fixed small-distance prism pair can be adjusted positively and negatively by changing the material dispersion, which can be changed by varying the passing through the length of the prism pair based on formulas (7)–(9). According to the simulation results, the second-order and third-order dispersions induced by prism pairs change continuously from positive to negative with increasing distance between prism pairs. When the prism pair distance reaches the meter-level unit, the second-order and third-order dispersions are both negative. At this time, the positive dispersion introduced by the stretcher and the material dispersion of the front components are pre-compensated. Meanwhile, we can fully compensate for the negative chirp with a thick glass plate [
25] so that the laser beam can be shaped spatially without changing the temporal characteristics. Note that grating pairs together with prism pairs are always used to fully compensate for the third-order dispersion of the whole laser system to achieve a short pulse duration with broad spectral bandwidth because the third-order dispersions induced by prism pairs and grating pairs are opposite [
26]. Then, the prism pair added before the grating-based compressor helps compensate for the third-order and even the fourth-order spectral dispersion in the PW laser [
26,
27].
5. Discussion and Conclusions
This study proposed a beam smoothing method based on prism pairs to reduce the hotspot intensity in high-peak-power laser beams due to the diffuse reflection of dust or defects in optical elements. The proposed method can prevent damage to the first and fourth gratings in the grating-based compression system. Furthermore, the factors influencing the smoothing beam based on the prism pair are explored. The simulation results demonstrate that LSIMR is closely related to the induced spatial dispersion width. The spatial dispersion width is found to be strongly correlated with the apex angle of the prism pair, the distance between the prism pair, and incident beam characteristics.
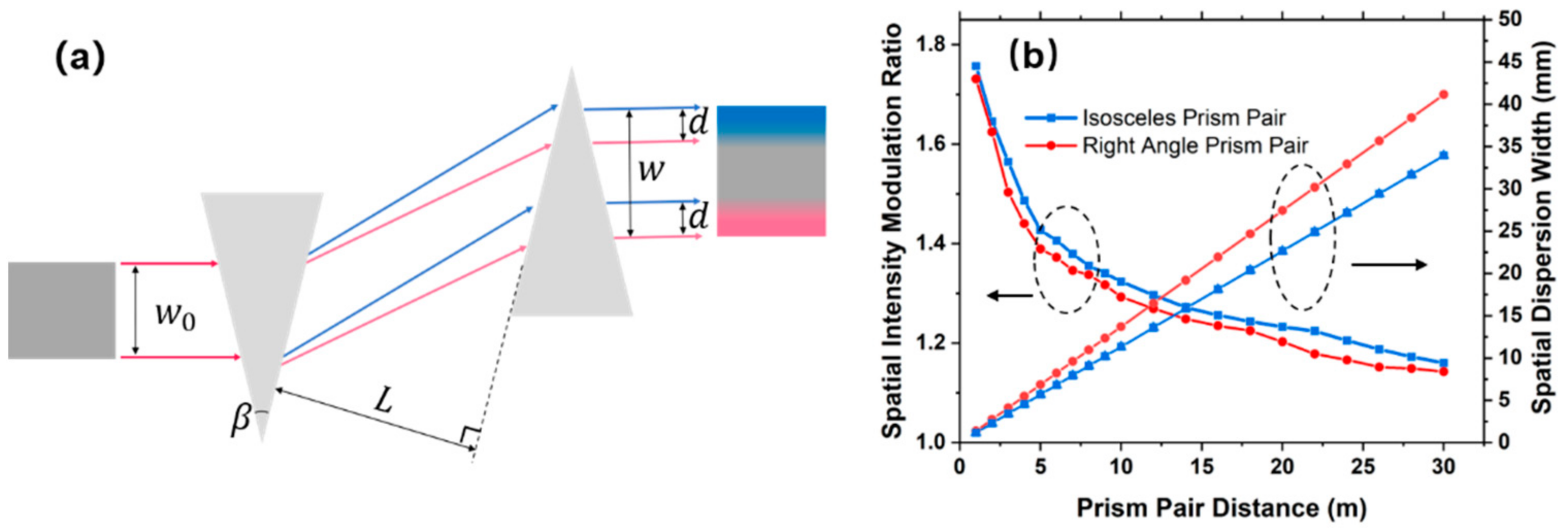
The laser beam smoothing effect of single as well as dual prism pairs are simulated. The two prism pairs proposed to introduce spatial dispersion can be divided into one and two directions. The simulation results demonstrated that the smoothing effect of the two prism pairs can achieve a larger spatial dispersion width using a relatively small experimental space. Finally, we simulate the spectral dispersion of the central wavelength after passing through a prism pair. Combining both the grating and prism pairs will also help compensate for the third-order spectral dispersion to achieve a short pulse duration with broad spectral bandwidth.
A prism pair with a small apex angle has the advantages of no aberration, simplicity, and energy efficiency and can be used for image transmission (without beam expansion). In the next design, the spatiotemporal focusing technique is used to self-compensate for the induced spatial dispersion during the post-compression process. In a real application, the beam, after passing through the prism pair to induce the dispersion for smoothing the beam profile, is filtered out at the edge to maintain the central region with full spectral bandwidth. The temporal contrast can be affected by the spatiotemporal aberration. These problems can be solved in the whole system design in Ref. [
15] by a reflective deformable mirror (DM). Actually, the induced spatial dispersion width is small in comparison to the beam size, and the transmitted light owning small wavefront distortion. Therefore, the use of a prism-pair smooth beam does not affect the characteristics of laser beams. The method proposed in this study is applicable and of significance in ultrashort pulse compression systems.